Пусть поставлена задача вида:
(1) 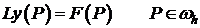 ;
;
(2) 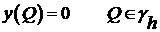 ,
,
с оператором из исходного семейства
(3)  .
.
Тогда имеет место оценка:
(4) 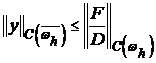 .
.
Доказательство.
А) Случай, когда  является тривиальным, т.к. задача (1), (2) удовлетворяет условиям следствия 2 теоремы 1:
является тривиальным, т.к. задача (1), (2) удовлетворяет условиям следствия 2 теоремы 1:  .
.
Тогда (4) есть равенство:
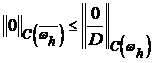 .
.
В) Случай, когда  . Следовательно, существует
. Следовательно, существует 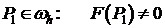 .
.
Рассмотрим для задачи (1), (2) вспомогательную задачу: (5), (6):
(5) 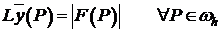 ,
,
(6)  .
.
Поскольку задачи (1), (2) и (5), (6) удовлетворяют в частности условиям теоремы 2, то справедливо неравенство:
(7)  ,
,
(8) 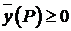 .
.
Пусть точка 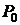 - точка в которой
- точка в которой 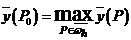 .
.
Покажем, что эта точка является внутренней точкой, т.е. не может быть граничной.
Предположим противное, т.е.  , тогда имеем неравенство:
, тогда имеем неравенство:
 .
.
Следовательно, 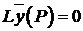 , что противоречит условию.
, что противоречит условию.
Запишем уравнение (5) в этой точке.
 .
.
Если в задаче (5), вместо  подставить
подставить  , тогда
, тогда
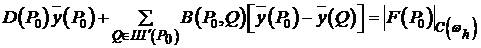 ,
,
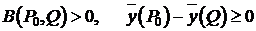 ,
,
 , т.к.
, т.к.  ,
,
 .
.
Так как  .
.
С другой стороны, 
 , в силу теоремы сравнения.
, в силу теоремы сравнения.
Заменяя 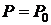 и переходя к максимуму, получаем:
и переходя к максимуму, получаем:
(10) 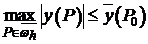 .
.
Теорема 4. Обобщение теоремы 3
Пусть поставлена задача вида:
(1) 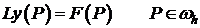 ;
;
(2) 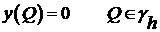 ,
,
с оператором 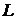 из исходного семейства.
из исходного семейства.
Имеется связная сетка 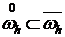 и
и 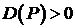 для
для 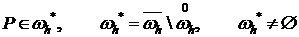
(3) Причем,  , если
, если  .
.
Тогда имеет место оценка:
(4)  .
.
______________________________________________________________
‼ 1)  - связная, или нет?
- связная, или нет?
2) К чему приведет устранение условия 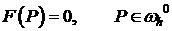 ?
?
3) Рассмотреть обобщение теоремы 3 на случай, ограничения на коэффициенты:

______________________________________________________________
Исследование устойчивости разностных схем на основе принципа максимума и следствий из него
Принцип максимума дает достаточные условия устойчивости по граничным данным и по правой части.
В ряде случаев можно получить устойчивость и по начальным данным, если начальные условия учесть в правой части.
Пример.
Рассмотрим непрерывную задачу:
(1) 
(2) 
Считаем, что уравнение невырожденное.
(3)  .
.
Поскольку коэффициенты постоянны, то
(4)  ,
,
(5)  .
.
Запишем дискретную задачу (4), (5) в канонической форме.
(6) 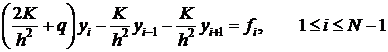
 ,
,
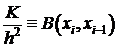 ,
, 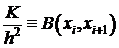 .
.
(7)  .
.
Поставим задачу.
Используя запись (6), (7), ограничения (3) требуется доказать устойчивость задачи (6), (7) по граничным данным и правой части.
Чтобы доказать устойчивость необходимо доказать неравенство:
(8) 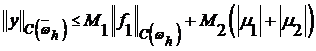 ,
,
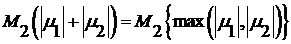 .
.
Рассмотрим две вспомогательные задачи:
I. 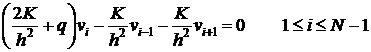
 .
.
Выполняются все условия теоремы сравнения (теорема 2), а именно:
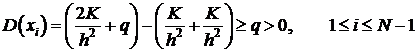 .
.
Для 
 .
.
Следовательно, из теоремы 2, получаем:
(9)  ,
,
 .
.
Неравенство (9) означает, что 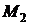 в доказанной оценке (8) равна 1.
в доказанной оценке (8) равна 1.
II.
(10) 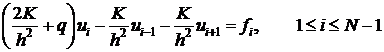
(11)  .
.
Очевидно, все условия теоремы 3 выполняются, следовательно, справедлива оценка:
 .
.
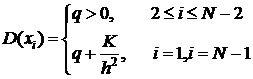 ,
,  .
.
(12)  ,
, 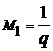 .
.
Из неравенства треугольника и оценок (12), (9) следует оценка:
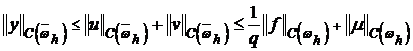 .
.
Полученная оценка может быть использована для доказательства сходимости.
Рассмотрим задачу для погрешности.
Введем погрешность:  .
.
 , подставим в исходную разностную схему (4), (5):
, подставим в исходную разностную схему (4), (5):
(4)  ,
,
(5)  .
.
(13)  ,
,
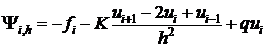
(14)  .
.
По структуре (13), (14) аналогична исходной разностной схеме, отличие состоит лишь в правых частях.

В правой части (13) стоит погрешность аппроксимации исходного разностного дифференциального уравнения разностной схемой на решении задачи.
Ранее было показано, что:
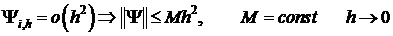
(12′) 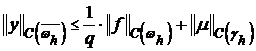 ,
, 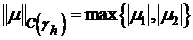 .
.
В соответствии с доказанным и неравенством (12′) получаем,

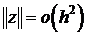 .
.
Примеры решения задач на принцип максимума и следствий из него
Используя принцип максимума, установить достаточное условие устойчивости явной схемы для однородного уравнения теплопроводности.
Пример 1.
(1) 
(2) 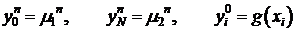 .
.
В канонической форме  .
.
Проверим:
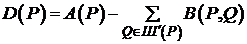
 .
.
Пусть  ,
,  .
.
Следовательно, не существует такого 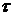 , чтобы
, чтобы  . Следовательно, либо Р неподходящее, либо схема не устойчива.
. Следовательно, либо Р неподходящее, либо схема не устойчива.
Возьмем 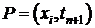 .
.
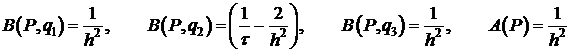 .
.
Схема будет из исходного семейства, если  , т.е.
, т.е. 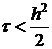 .
.
Замечание.
Интересно отметить, что такое же ограничение будет получено энергетическим методом для исследования устойчивости.
Во внутренних узлах сетки 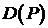 :
:
(3) 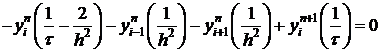 .
.
К полученной задаче применим следствие 4 теоремы 1.
Поэтому 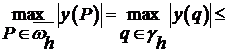 . (*)
. (*)
Границей для данной сеточной задачи является множество узлов: 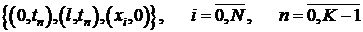 .
.
Предполагается, что условия согласованны.
(*) 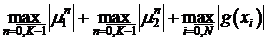 .
.
Второй способ предпочтительнее.
Непосредственно учитываем граничные условия (2) в уравнении (1).
Для 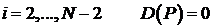 как и ранее.
как и ранее.
В точке 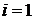 получим (3) в виде:
получим (3) в виде:
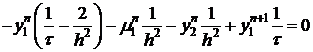
Получим каноническую форму.
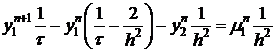 .
.
Уравнение необходимого условия, следовательно,
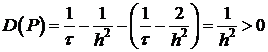 .
.
В точке 
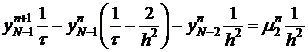 .
.
Следовательно, 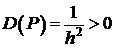 .
.
В точках 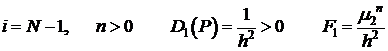 ,
,
 .
.
В точках  имеем:
имеем:
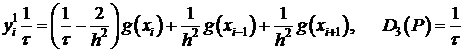 .
.
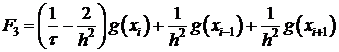 .
.
Формально считаем, что все 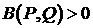 , т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
, т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
В силу теоремы 4
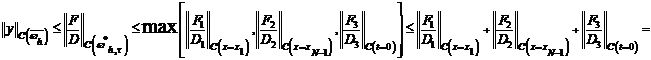
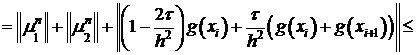
воспользуемся неравенством многоугольников и тем, что 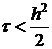 получим
получим 
Пример 2.
(1) 
(2) 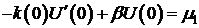
(3) 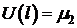 .
.
Так как коэффициенты постоянные, то будем использовать аппроксимацию
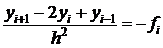 ,
,
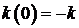 ,
,
 .
.
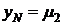
Для повышения порядка можно взять 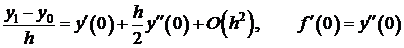 .
.
Разобьем нашу задачу на две, представив решение в виде: 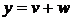 .
.
I. 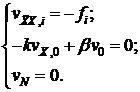
II. 
Разделим (2) на к и переобозначим, получим:
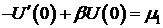
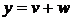 ;
;
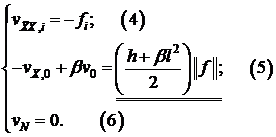
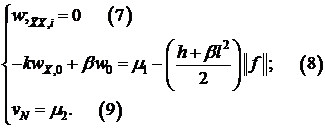
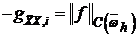 ,
,
 , продифференцируем.
, продифференцируем.
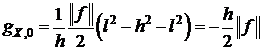 .
.
 .
.
Для задачи (4) – (6) сформулируем вспомогательную задачу:

Последняя задача имеет решение:  .
.
В силу теоремы сравнения
(10)  .
.
Займемся задачей (7), (8), (9), ориентируясь на теорему 4.
Уравнение (7) из исходного семейства
 в котором
в котором  и
и 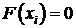 .
.
Займемся точкой  , используя равенство (8).
, используя равенство (8).
 ;
;
 ;
;
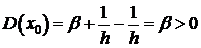 .
.
Таким образом  .
.
Запишем уравнение (7) в 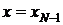 .
.
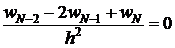 ;
;
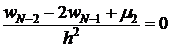 ;
;
 ;
;

Исследование устойчивости закончено, если учесть, что
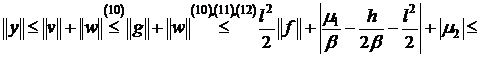 используем неравенство треугольников
используем неравенство треугольников 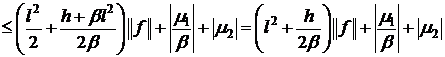 .
.
 .
.



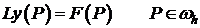 ;
;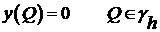 ,
, .
.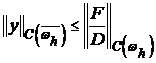 .
. является тривиальным, т.к. задача (1), (2) удовлетворяет условиям следствия 2 теоремы 1:
является тривиальным, т.к. задача (1), (2) удовлетворяет условиям следствия 2 теоремы 1:  .
.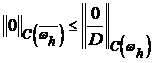 .
. . Следовательно, существует
. Следовательно, существует 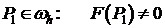 .
.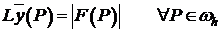 ,
, .
. ,
,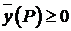 .
.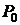 - точка в которой
- точка в которой 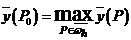 .
. , тогда имеем неравенство:
, тогда имеем неравенство: .
.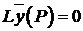 , что противоречит условию.
, что противоречит условию. .
. подставить
подставить  , тогда
, тогда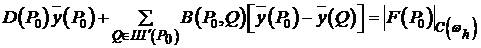 ,
,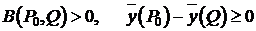 ,
, , т.к.
, т.к.  ,
, .
. .
.
 , в силу теоремы сравнения.
, в силу теоремы сравнения.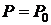 и переходя к максимуму, получаем:
и переходя к максимуму, получаем: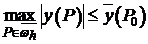 .
.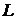 из исходного семейства.
из исходного семейства.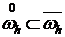 и
и 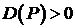 для
для 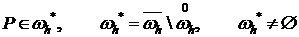
 , если
, если  .
. .
. - связная, или нет?
- связная, или нет?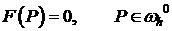 ?
?


 .
. ,
, .
.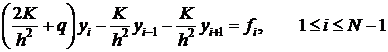
 ,
,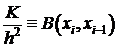 ,
, 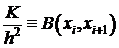 .
.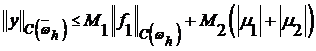 ,
,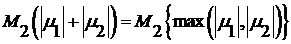 .
.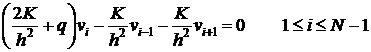
 .
.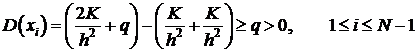 .
.
 .
. ,
, .
.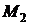 в доказанной оценке (8) равна 1.
в доказанной оценке (8) равна 1.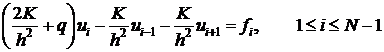
 .
. .
.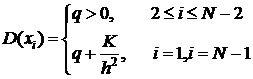 ,
,  .
. ,
, 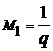 .
.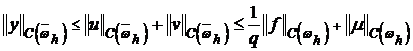 .
. .
. , подставим в исходную разностную схему (4), (5):
, подставим в исходную разностную схему (4), (5): ,
,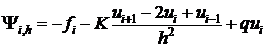
 .
.
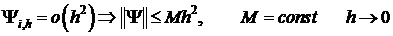
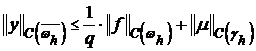 ,
, 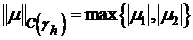 .
.
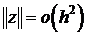 .
.
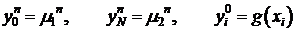 .
. .
.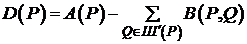
 .
. ,
,  .
.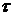 , чтобы
, чтобы  . Следовательно, либо Р неподходящее, либо схема не устойчива.
. Следовательно, либо Р неподходящее, либо схема не устойчива.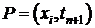 .
.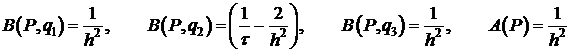 .
. , т.е.
, т.е. 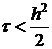 .
.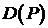 :
: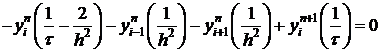 .
.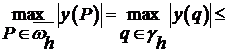 . (*)
. (*)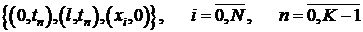 .
.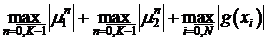 .
.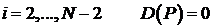 как и ранее.
как и ранее.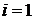 получим (3) в виде:
получим (3) в виде: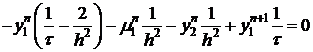
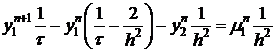 .
.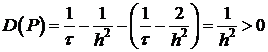 .
.
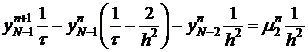 .
.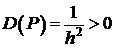 .
.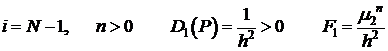 ,
, .
. имеем:
имеем: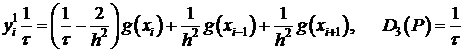 .
.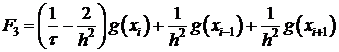 .
.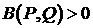 , т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
, т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.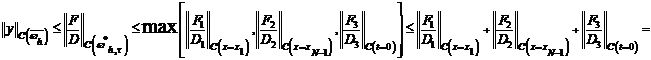
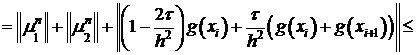


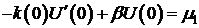
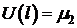 .
.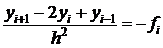 ,
,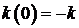 ,
,  .
.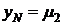
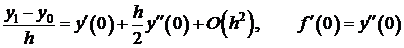 .
.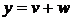 .
.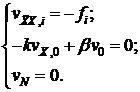

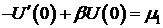
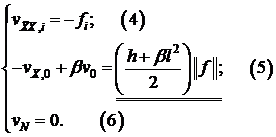
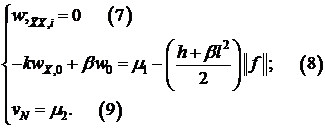
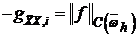 ,
, , продифференцируем.
, продифференцируем.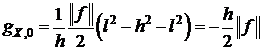 .
. .
.
 .
. .
. в котором
в котором  и
и 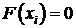 .
. , используя равенство (8).
, используя равенство (8). ;
; ;
;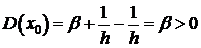 .
. .
.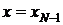 .
.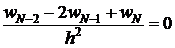 ;
;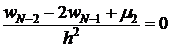 ;
; ;
;
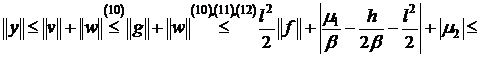 используем неравенство треугольников
используем неравенство треугольников 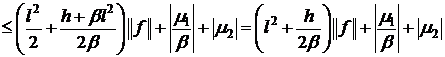 .
. .
.

