Учитывая сложность доказательства достаточного условия экстремума функции даже двух переменных, приведем его без доказательства для функции 2-х переменных.
Обозначим частные производные второго порядка функции z = z(x;y):

Теорема. Для того чтобы в точке, подозрительной на экстремум, функция z = z (x; y) принимала максимальное или минимальное значение достаточно чтобы выполнялось условие A · C – B 2 > 0. Причем, если A < 0 (C < 0), то максимум, если A > 0 (C > 0), то минимум. Если A · C – B 2 < 0, то экстремума нет, если A · C – B 2 = 0, то требуются другие исследования.
Примеры. Проверим достаточное условие экстремума функции z = x2 +2xy + 4y0.5, учитывая первые производные, полученные выше. Найдем вторые производные: 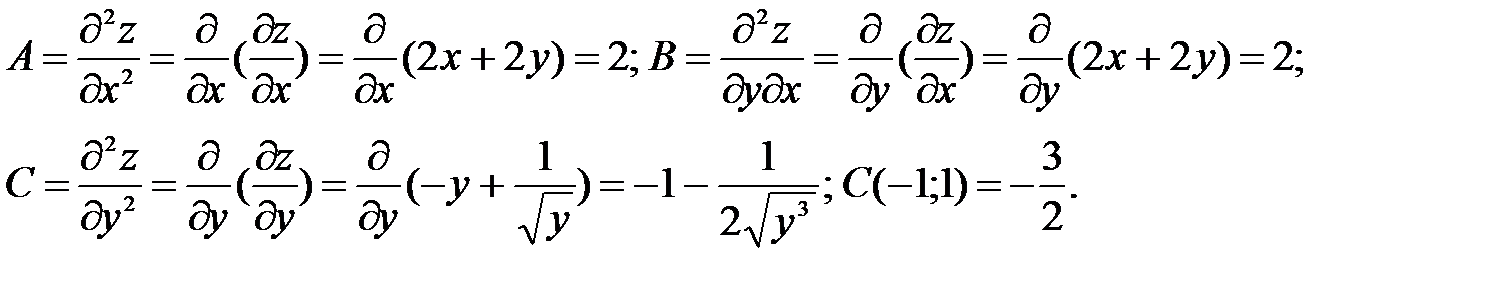
Проверим условие A·C – B2 = 2·(-1.5) – (2)2 = -3 – 4 < 0. Экстремума в точке (-1;1) – нет.
2. Найти экстремум функции z = sinx + siny + sin(x + y), если 0 <x+y<π/2.
Найдем частные производные функции zx = cosx+cos(x+y); zy = cosy + cos(x+y). Приравняем их нулю и найдем значения переменных:
zx = cosx+cos(x+y) = 0,
zy = cosy + cos(x+y) = 0.
Вычтем одно равенство из другого и получим уравнение: cosx = cosy, решая которое, получим x = ±y + 2πn. Учитывая условие задачи 0 <x+y<π/2, получим x = y и x = - y. Подставим первое равенство в одно из уравнений: cosx + cos2x = 0, 2cos1.5x·cos0.5x = 0. Приравнивая каждый сомножитель нулю, получим 1.5x = π/2, 0.5x = π/2. Учитывая условие задачи 0 <x+y<π/2, находим точку P(π/3;π/3), в которой частные производные обращаются в ноль. Проверим достаточное условие A·C – B2 > 0, для чего вычислим вторые производные: 
Таким образом, достаточное условие экстремума в точке Р выполняется, и в этой точке функция принимает максимальное значение, так как A < 0 (C<0).
§22. Локальный экстремум функции двух переменных.
В задачах науки и техники нередко возникает задача отыскания экстремума функции многих переменных на точках подмножества множества определения функции. В частности, для функции 2-х переменных таким подмножеством может являться множество точек какой-либо линии. Например, определить экстремум функции  на множестве точек прямой
на множестве точек прямой
x + y = 2.
На рисунке 5 видно, что плоскость x+y-2=0 на сфере вырезает кривую, которая достигает максимума в точке прямой x + y = 2. Нетрудно видеть, что локальный экстремум в общем случае не совпадает с безусловным экстремумом. Безусловный экстремум может быть условным.
Рассмотрим методы вычисления условных экстремумов для функции 2-х переменных.
Пусть задана функция z = z(x,y) и некоторая кривая, называемая уравнением связи.
1.Если уравнение связи задано в явном виде y = f(x), то его (уравнение связи) подставляем в выражение функции z = z(x,y) и получим функцию одной переменной z = z(x,f(x)), отыскание экстремума которой известно. Так, в выше приведенном примере из уравнения связи выразим одну переменную через другую y = 2 – x и подставим в функцию: 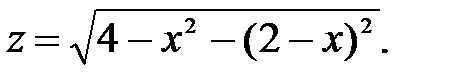 Найдем производную этой функции и приравняем ее нулю:
Найдем производную этой функции и приравняем ее нулю:  В результате решения получим x = 1, а подставляя в уравнение связи, находим ординату точки y = 1. Нетрудно проверить и выполнение достаточного условия. Итак, в точке P(1;1), принадлежащей прямой x + y = 2, получен максимум функции z =
В результате решения получим x = 1, а подставляя в уравнение связи, находим ординату точки y = 1. Нетрудно проверить и выполнение достаточного условия. Итак, в точке P(1;1), принадлежащей прямой x + y = 2, получен максимум функции z = 
2. Если уравнение связи задано в параметрическом виде  то и в этом случае после подстановки в уравнение функции получим функции одной переменной z = z(x(t),y(t)).
то и в этом случае после подстановки в уравнение функции получим функции одной переменной z = z(x(t),y(t)).
3. Пусть теперь уравнение связи задано в неявном виде φ(x,y) = 0. Считая в функции z = z(x,y) переменную y функцией x, найдем полную производную по x:
 (51)
(51)
Из уравнения связи φ(x,y) = 0, найдем производную
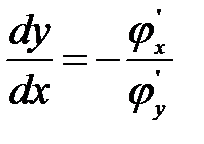 . (52)
. (52)
Производная (51) в точках условного экстремума должна быть равна нулю и вместе с уравнением связи получим систему двух уравнений. После подстановки (52) в (51) и преобразований получим
 (53)
(53)
неизвестную λ:  . В результате получим систему трех уравнений:
. В результате получим систему трех уравнений:
 (54)
(54)
Для более легкого запоминания системы (54) введем вспомогательную функцию6
Ф(x,y,λ) = z(x,y) + λ φ(x,y). (55) Отыскивая экстремум этой функции трех переменных, получим систему (54), которая выражает необходимое условие экстремума функции (55). Однако, не всякая пара x и y, являющихся решением системы (54), определяет точку экстремума. Достаточное условие условного экстремума не приводим; часто само содержание задачи подсказывает, чем является точка. Изложенный метод решения задач на условный экстремум называется методом множителей Лагранжа.
Пример. Найти точки условного экстремума функции z = 4 – x – y на множестве точек кривой (уравнение связи) 
Составим функции Ф(x,y,λ) = 4-x-y-λ(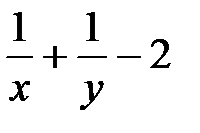 ) и систему (54). Получим –
) и систему (54). Получим –
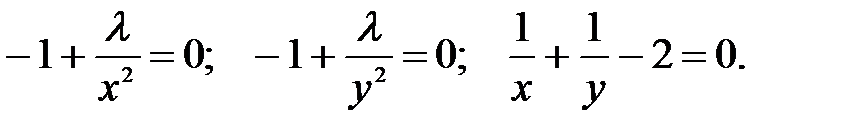
 Решая первые два уравнения, получим x = y и x = -y. Подставляя x = y в третье, найдем x = 1, y = 1. Эта точка является точкой условного экстремума. Решение x = -y не удовлетворяет уравнению связи.
Решая первые два уравнения, получим x = y и x = -y. Подставляя x = y в третье, найдем x = 1, y = 1. Эта точка является точкой условного экстремума. Решение x = -y не удовлетворяет уравнению связи.
Лекция 12. §23 Скалярное поле
Предположим, что в каждой точке P области D задано значение скалярной физической величины u. Например, эта может быть температура неравномерно нагретого тела, потенциал электрического поля и т.д. В этом случае u называется скалярной функцией точки и обозначается как u = u (P).
Определение. Если в области D задана скалярная функция точки u (P), то говорят, что в этой области задано скалярное поле.
Область D может совпадать со всем пространством и может быть частью его. Если скалярное поле не зависит от времени, то оно называется стационарным. Если скалярное поле отнесено к системе координат Oxyz, то задание точки P равносильно заданию ее координат x, y, z; и тогда функцию u(P) можно записать в обычно виде как функцию трех переменных u(x,y,z).
Определение. Поверхностью уровня скалярного поля называется геометрического место точек, в которых скалярная функция u принимает постоянное одинаковое значение u (x, y, z) = C.
Уравнение поверхности уровня, проходящей через заданную точку M(x0,y0,z0) записывается так: u(x,y,z) = u(x0,y0,z0).
Если скалярное поле плоское, то скалярная функция имеет вид u = u(x,y), а линия уровня u(x,y) = u(x0,y0).
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении. Пусть задано скалярное поле, т.е. задана скалярная функция u = u(x,y,z). Выберем произвольную точку P(x,y,z) и какое-либо направление λ. Пусть направление λ задано единичным вектором eλ(cosα, cosβ, cosγ) (рис.6). Зададим на напра
влении λ выбрана точка P
0(x
0,y
0,z
0). Обозначим расстояние между точками P(x,y,z) и P
0(x
0,y
0,z
0) через ρ =

. Нетрудно видеть, что проекции вектора
PP 0 на оси координат будут с одной стороны x
0 – x, y
0 – y, z
0 – z, с другой - ρ·cosα, ρ·cosβ, ρ·cosγ соответственно. Поэтому x
0 = x + ρ·cosα, y
0 = y + ρ·cosβ, z
0 = z + ρ·cosγ. Тогда приращение функции u(x,y,z): ∆u = u(x
0,y
0,z
0) - u(x,y,z) = u(x+ ρ·cosα,y+ ρ·cosβ,z+ ρ·cosγ)- u(x,y,z). Или ∆u=u(P
0)- u(P)
Когда точка P0 приближается к точке P вдоль направления λ, то меняется только расстояние ρ.
Определение. Производной по направлению λ называется предел отношения приращения скалярной функции u (x, y, z) к расстоянию между точками, когда расстояние стремится к нулю.
Этот предел принято обозначать  По определению производной, учитывая приращение скалярной функции –
По определению производной, учитывая приращение скалярной функции –
 (56)
(56)
Следует заметить, что частные производные, рассмотренные выше, являются частными случаями производной по направлению. Действительно. Выберем направлением ось Ox: cosα = cos0 = 1, cosβ= cosγ = cosπ/2=0, ρ = x0 – x = ∆x. Тогда
Выведем формулу вычисления производной по направлению, для чего заменим приращение функции дифференциалом и бесконечно малой ε(ρ) –
 Подставим правую часть равенства в выражение производной (56) и получим –
Подставим правую часть равенства в выражение производной (56) и получим –
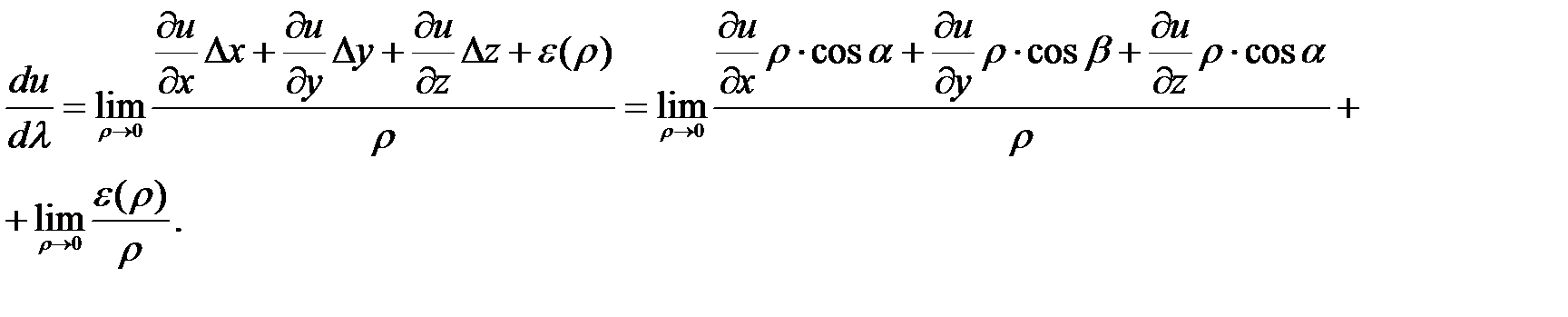 Учитывая, что частные производные не зависят от ρ, а второй предел равен нулю, производная по направлению выразится как
Учитывая, что частные производные не зависят от ρ, а второй предел равен нулю, производная по направлению выразится как
 (57)
(57)
Итак, производная по направлению равна сумме произведений частных производных скалярной функции на соответствующие направляющие косинусы направления.
Пример. Вычислить производную функции u = x2y + z3 в точке B(2,-1,3) в направлении от A(-2, -3,-1) к B.
Решение. Вычислим частные производные функции и их значения в точке B:

направления eλ (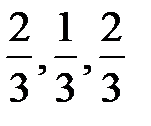 ). Таким образом,
). Таким образом,
uλ =(-2·2+4·1+27·2)/3=18.
Замечание. При изменении направления производная в точке меняет знак на противоположный.
Анализируя формулу производной по направлению (57) можно заметить, что правая часть ее есть скалярное произведение двух векторов в координатной форме.
Определение. Вектор, составленный из частных производных скалярной функции, называется градиентом и обозначается grad u или  .
.
Следовательно, производную (57) можно теперь записать так:
uλ = (grad u · eλ) или uλ = | grad u |·| eλ |· cos φ = | grad u |· cos φ, (58)
где φ – угол между векторами (рис.7), | eλ | = 1.
Из рисунка 7 и формулы (58) видно, что производная по направлению становится максимальной, если направление совпадает с направлением градиента.
Итак, направление градиента определяет максимальную скорость изменения скалярного поля в заданной точке, а модуль градиента значение этой скорости.
В этом состоит физический смысл градиента.




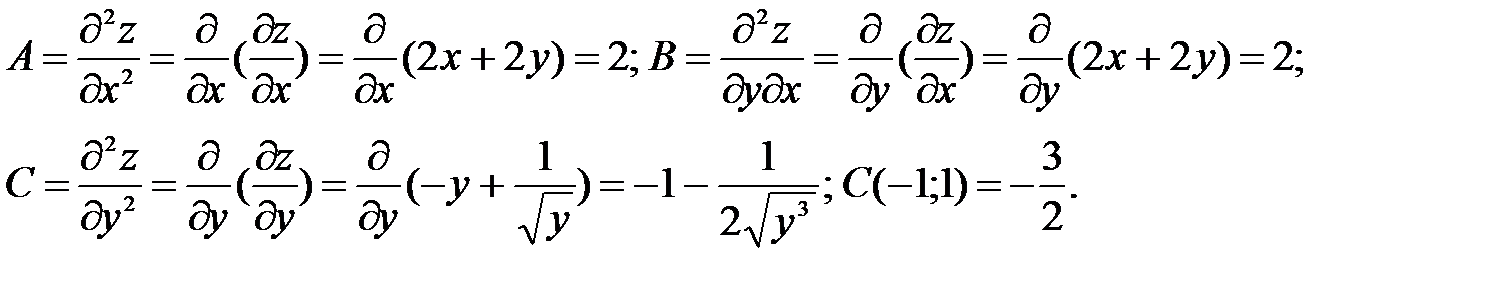

 на множестве точек прямой
на множестве точек прямой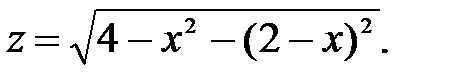 Найдем производную этой функции и приравняем ее нулю:
Найдем производную этой функции и приравняем ее нулю:  В результате решения получим x = 1, а подставляя в уравнение связи, находим ординату точки y = 1. Нетрудно проверить и выполнение достаточного условия. Итак, в точке P(1;1), принадлежащей прямой x + y = 2, получен максимум функции z =
В результате решения получим x = 1, а подставляя в уравнение связи, находим ординату точки y = 1. Нетрудно проверить и выполнение достаточного условия. Итак, в точке P(1;1), принадлежащей прямой x + y = 2, получен максимум функции z = 
 то и в этом случае после подстановки в уравнение функции получим функции одной переменной z = z(x(t),y(t)).
то и в этом случае после подстановки в уравнение функции получим функции одной переменной z = z(x(t),y(t)). (51)
(51)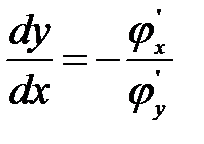 . (52)
. (52) (53)
(53) . В результате получим систему трех уравнений:
. В результате получим систему трех уравнений: (54)
(54)
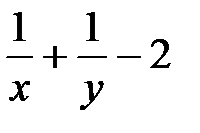 ) и систему (54). Получим –
) и систему (54). Получим –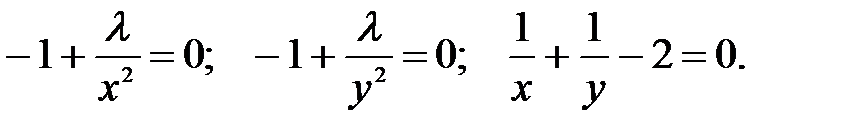
 Решая первые два уравнения, получим x = y и x = -y. Подставляя x = y в третье, найдем x = 1, y = 1. Эта точка является точкой условного экстремума. Решение x = -y не удовлетворяет уравнению связи.
Решая первые два уравнения, получим x = y и x = -y. Подставляя x = y в третье, найдем x = 1, y = 1. Эта точка является точкой условного экстремума. Решение x = -y не удовлетворяет уравнению связи. . Нетрудно видеть, что проекции вектора PP 0 на оси координат будут с одной стороны x0 – x, y0 – y, z0 – z, с другой - ρ·cosα, ρ·cosβ, ρ·cosγ соответственно. Поэтому x0 = x + ρ·cosα, y0 = y + ρ·cosβ, z0 = z + ρ·cosγ. Тогда приращение функции u(x,y,z): ∆u = u(x0,y0,z0) - u(x,y,z) = u(x+ ρ·cosα,y+ ρ·cosβ,z+ ρ·cosγ)- u(x,y,z). Или ∆u=u(P0)- u(P)
. Нетрудно видеть, что проекции вектора PP 0 на оси координат будут с одной стороны x0 – x, y0 – y, z0 – z, с другой - ρ·cosα, ρ·cosβ, ρ·cosγ соответственно. Поэтому x0 = x + ρ·cosα, y0 = y + ρ·cosβ, z0 = z + ρ·cosγ. Тогда приращение функции u(x,y,z): ∆u = u(x0,y0,z0) - u(x,y,z) = u(x+ ρ·cosα,y+ ρ·cosβ,z+ ρ·cosγ)- u(x,y,z). Или ∆u=u(P0)- u(P)
 По определению производной, учитывая приращение скалярной функции –
По определению производной, учитывая приращение скалярной функции – (56)
(56) Подставим правую часть равенства в выражение производной (56) и получим –
Подставим правую часть равенства в выражение производной (56) и получим –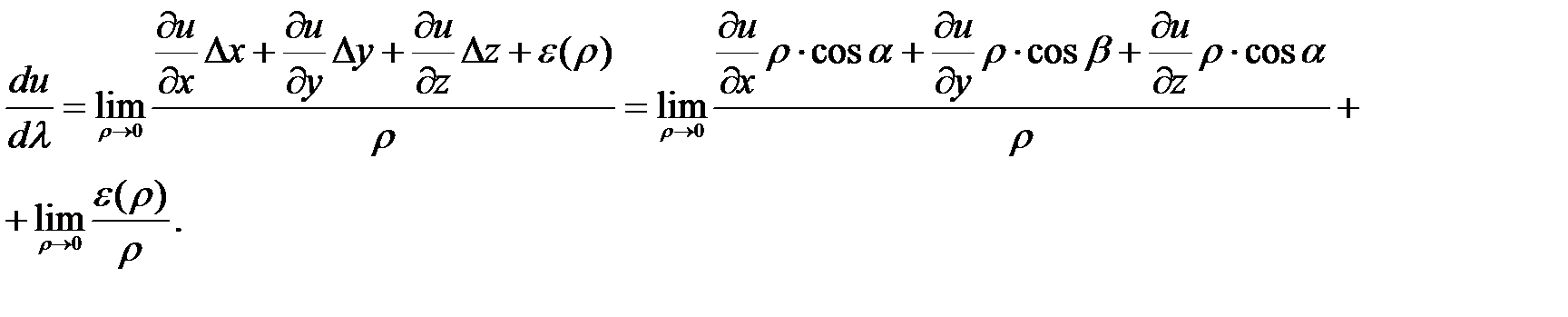 Учитывая, что частные производные не зависят от ρ, а второй предел равен нулю, производная по направлению выразится как
Учитывая, что частные производные не зависят от ρ, а второй предел равен нулю, производная по направлению выразится как (57)
(57)
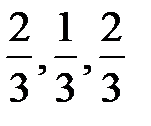 ). Таким образом,
). Таким образом, .
.


