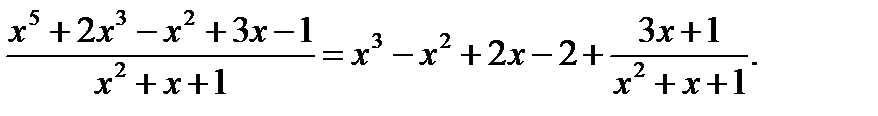∫ (u + v + s +…….+r) dx = ∫ udx+∫ vdx+∫ sdx+………+∫ rdx,
где u, v, s,…….,r – функции независимой переменной x.
Действительно, если продифференцировать обе части равенства, то, учитывя свойства производной и свойство 1, получим
(∫ (u + v + s +…….+r) dx)’ = (∫ udx)’+(∫ vdx)’+(∫ sdx)’+………+(∫ rdx)’=u + v + s +…….+r. Свойство доказано.
Три последних свойства широко используют, отыскивая первообразные.
Для того, чтобы активно использовать третье свойство напомним свойства дифференциала: дифференциал постоянной равен нулю; постоянный множитель можно выносить из под знака дифференциала; дифференциал суммы переменных равен сумме дифференциалов; выражение под дифференциалом можно умножать и делить на одно и тоже число.
На основании этих свойств имеют место следующие равенства: d(a+x)=dx=d(b+x); Другими словами, под знак дифференциала можно вносить в качестве слагаемого любую константу. a · d 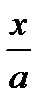 =
= 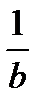 d b x =
d b x = 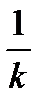 d(kx + b) = dx.
d(kx + b) = dx.
Теорема об инвариантности формул интегрирования.
Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от независимой переменной т.е. если
∫ f (x) dx = F (x) + C, то и ∫ f (u) du = F (u) + C,
где u = φ (x) – любая дифференцируемая функция от x.
Доказательство. Пусть ∫f(x)dx = F(x) + C. Следовательно, F’(x) = f(x). Возьмем теперь функцию F(u) =F[φ(x)] и дифференциал от нее dF(u) =(Fu)’φ’dx= (Fu)’du=f(u)du. Отсюда ∫f(u)du = F(u) + C, что и требовалось доказать.
На основании этой теоремы таблицу основных интегралов представим, считая u=u(x) функцией независимой переменной.
Таблица №1. Основная таблица интегралов
| №
| Интеграл
| Первообразная +С
| №
| Интеграл
| Первообразная + С
|
| 1
| ∫(u) ndx
| 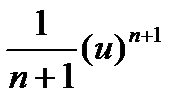 +C +C
| 10
| ∫ 
| arctg(u) +C
- arcctg(u) +C
|
| 2
| ∫Sin(u)du
| -Cos(u) + C
| 11
| ∫sh(u)du
| ch(u) + C
|
| 3
| ∫Cos(u)du
| Sin(u) + C
| 12
| ∫ch(u)du
| sh(u) + C
|
| 4
| ∫ 
| tg(u) + C
| 13
| ∫ 
| th(u) + C
|
| 5
| ∫ 
| -ctg(u) +C
| 14
| ∫ 
| -cth(u) + C
|
| 6
| ∫ 
| 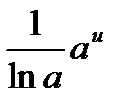 +C +C
| 15
| ∫ 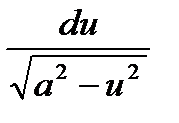
| arcsin 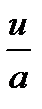 + C + C
|
| 7
| ∫ 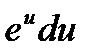
| eu+C
| 16
| ∫ 
|  + C + C
|
| 8
| ∫ 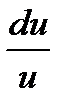
| lu(u) + C
| 17
| ∫ 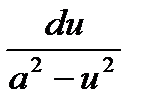
| 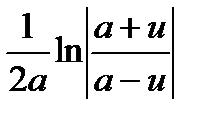 +C +C
|
| 9
| ∫ 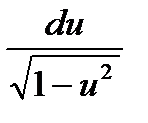
| arcsin(u) +C
- arccos(u) +C
| 18
| ∫ 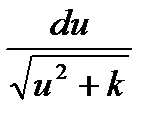
| ln|u+  | + C | + C
|
Примеры. 1. ∫(3x5+2Cosx)dx=3∫x5dx+2∫Cosxdx = x6/2 + 2Sinx + C.
2. ∫3x2ex3dx =∫ ex3dx3 = ∫ dex3 = ex3 + C. 3. ∫ (2-7x)1/2dx = 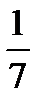 ∫ (2-7x)1/2d(2-7x) =
∫ (2-7x)1/2d(2-7x) =
= 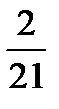 ∫d (2-7x)3/2 =
∫d (2-7x)3/2 = 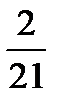 (2 -7x)3/2 + C.
(2 -7x)3/2 + C.
Примеры 2 и 3 можно было бы проинтегрировать, применяя метод замены переменной.
Лекция 2.
§2 Интегрирование методом замены переменной (метод подстановки) и
методом по частям.
Метод замены переменной. Заключается в замене части подынтегральной функции (подынтегрального выражения) или аргумента сложной функции. Выбор замены следует производить таким образом, чтобы после замены подынтегральное выражение соответствовало выражениям табличных интегралов. Производя замену, необходимо все подынтегральные функции и дифференциал выразить через новую переменную. Нередко, признаком замены является наличие степеней с разницей в единицу. Особенно, если аргументом функции является высшая степень. Так, в примере 2 - ∫3x2ex3dx сделаем замену t = x3, dt = 3x2dx и интеграл принимает вид табличного ∫3x2ex3dx = ∫etdt. В третьем примере ∫ (2-7x)1/2dx заменим подкоренную функцию t =2-7x. Дифференцируя замену, получим dt = -7dx или dx = -dt/7. После подстановки получим ∫ (2-7x)1/2dx = - 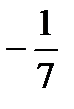 ∫ t1/2dt интеграл, который также является табличным.
∫ t1/2dt интеграл, который также является табличным.
Выбор замены представляется сложной процедурой и лучше удается при знании табличных интегралов. Во всяком случае, замене подлежат те функции, которые мешают интегралу быть табличным, или замена которых упрощают интегрируемую функцию. Например ∫ 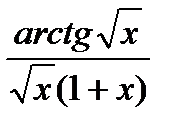 dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену
dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену 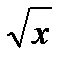 = t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫
= t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫ 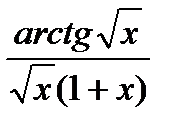 dx = ∫
dx = ∫  2tdt = 2∫
2tdt = 2∫ 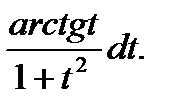 Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫
Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫ 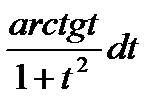 =
=
2∫tdt = t2 + C = arctg2t+ C.
В приведенных примерах использована замена вида u = φ(x). Покажем теперь применение замены вида x = g(u) на примере ∫Cos3 xdx. Представим функцию Cos3 x в виде Cos3 x = Cos2 x·Cosx = (1 – Sin2x)Cosx и произведем замену u = Sinx, du = Cos xdx. После подстановки получим:∫Cos3xdx =∫(1 – Sin2x)Cosxdx =∫(1 – u2)du=∫du-∫u2du=u-u3/3+C Обратную замену можно не производить, учитывая дальнейшее применение неопределенного интеграла при решении практических задач.
Замечание 1. Если функция f (x) имеет своей первоорбразной функцию F (x), то первоорбразной функции f (α x + β) будет функция 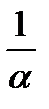 F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx =
F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx = 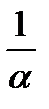 F(αx+β) + C.
F(αx+β) + C.
Замечание 2. Если числитель подынтегральной функции является производной знаменателя, то первообразная является логарифмом знаменателя, т.е. если f’(x)=φ(x), то 
Примеры. 
§3. Метод интегрирования по частям.
Метод основан на формуле вычисления дифференциала произведения двух функций u =u(x), v = v(x): d(u·v) = u·dv + v·du, u·dv = d(u·v) - v·du. Интегрируя обе части последнего равенства, получим
∫u·dv = ∫d(u·v) - ∫v·du
или ∫ u · dv = u · v - ∫ v · du (4)
Формула (4) носит название формулы интегрирования по частям. Интегрирование по частям состоит в том, что подынтегральное выражение f(x)dx представляется в виде произведения u·dv, выбирая в качестве u(x) такую функцию, дифференциал которой упрощает интеграл правой части (4). Аналогично - выражение dv интегрированием также упрощает интеграл правой части.
Во всяком случае, если подынтегральное выражение является произведением многочлена Pn(x) на дифференциалы вида eβx, Sinβx, Cosβx, то за u принимают многочлен Pn(x) и применяют формулу до тех пор, пока производная от многочлена не станет константой.
Пример. ∫(x2-3)·Cos2xdx=  =
= 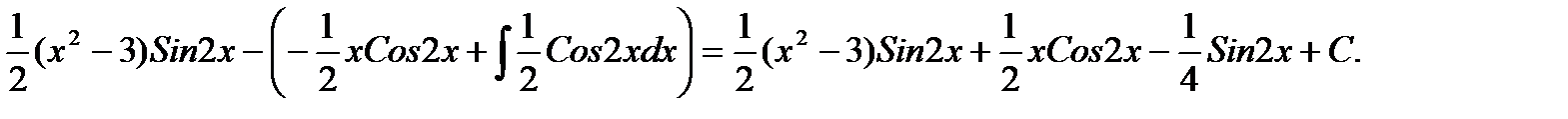
Если подынтегральное выражение включает одну из трансцендентных функций lnx, arccos(αx), arcsin(αx), arctgβx, то их надо принимать за u, так как производные от них более простые функции.
Пример. 2 ∫xarctgxdx =  = =x2arctgx – x +arctgx + C.
= =x2arctgx – x +arctgx + C.
Во всяком случае, признаком применения формулы интегрирования по частям может служить различная классификация функций, входящих в подынтегральную функцию. Например: многочлен и показательная; многочлен и трансцендентная.
§4. Интегрирование тригонометрических функций вида f(x)=Sinnx·Cosmx.
Универсальная подстановка.
Пусть подынтегральная функция f (x)= Sinnx · Cosmx, где показатели степеней – целые положительные числа. Интегрируя такие функции, следует различать два случая. 1. Показатели степеней четные, т.е. n = 2k, m = 2r. В этом случае порядок степеней следует понизить, применив формулы:
Sin2x = (1 – Cos2x)/2; Cos2x = (1 + Cos2x)/2 (5) преобразования подынтегральная функция будет представлять собой сумму произведений и, если показатели сомножителей вновь будут четными, то операцию понижения степени следует повторить. 2. Второй случай – один (оба) показатель (ля) нечетные. Тогда сомножитель с нечетным показателем (когда оба, неважно с каким) представляют в виде произведения одного сомножителя и сомножителя четной степени. Так, если например n = 2k + 1, то Sin2k+1x = Sin2kx·Sinx, после чего производят замену t = Cosx. Учитывая, что dt = dCosx = -Sinxdx, Sin2x = 1 – Cos2x = 1 – t2, подынтегральная функция станет многочленом переменной t. Действия аналогичны, если Cosmx = Cos2r+1x=Cos2rx·Cosx
Примеры. ∫Cos4xSin2xdx = ∫ 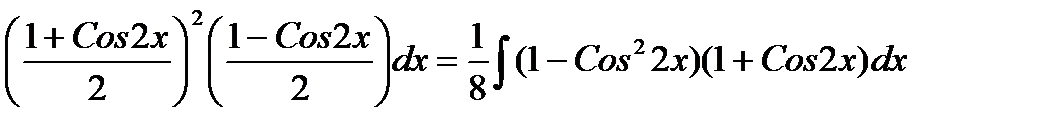 =
= 
= 
∫Cos3xSin2xdx = ∫Cos2xSin2xCosxdx = ∫(1-Sin2x)Sin2xdSinx = 
Интегралы ∫R(Sinαx;Cosαx)dx, подынтегральная функция которых является рациональной функцией переменных Sinαx и Cosαx сводятся к интегрированию рациональной функции одной переменной заменой, называемой универсальной, -
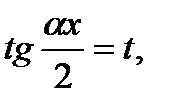 (6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =
(6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =  (7) Разрешим формулу (6) относительно независимой переменной -
(7) Разрешим формулу (6) относительно независимой переменной - 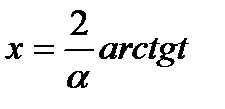 и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной
и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной  (8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
(8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
∫R(Sinαx;Cosαx)dx =  (9)
(9)
Пример. ∫ 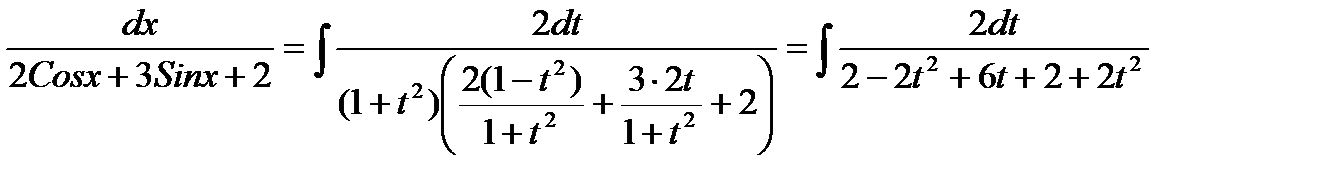 =
=
= 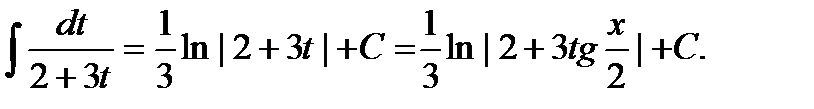
В случае, когда функции Sinαx и Cosαx входят в рациональную функцию R(Sinαx;Cosαx) в четных степенях, то применят замену
t = tgαx, (10)
учитывая, что  (11)
(11)
Пример. 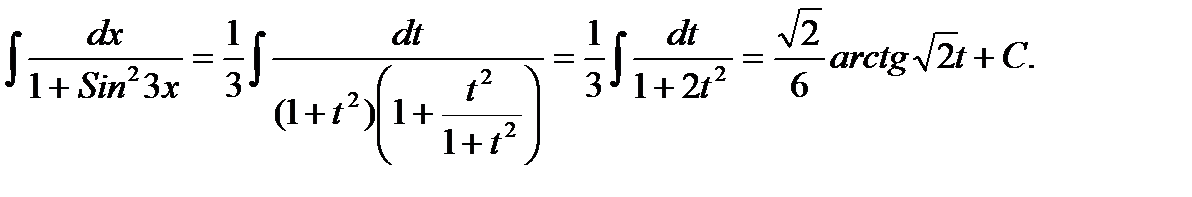
Лекция 3
§5. Интегрирование дробно-рациональных функций.
Определение. Отношение двух многочленов одной переменной называется дробно-рациональной функцией или рациональной дробью.
Определение. Дробь называется неправильной, если порядок многочлена числителя больше или равен порядка многочлена знаменателя, и правильной, если меньше.
Теорема. Любую неправильную дробь можно представить в виде суммы многочлена и правильной дроби, т.е. если f(x) =  гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то
гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то 
Пусть Pn(x) = x5 + 2x3 – x2 + 3x – 1; Qm(x) = x2 + x + 1. Представим неправильную дробь

 как сумму многочлена и правильной дроби, разделив многочлены уголком:
как сумму многочлена и правильной дроби, разделив многочлены уголком:
x5 +0x4 + 2x3 – x2 + 3x – 1| x 2 + x + 1
x 5 +0 x 4 + x 3 x3 – x2 +2x - 2
-x4 + x3 – x2
- x 4 - x 3 - x 2
2x3 - 0x2 + 3x
2 x 3 + 2 x 2 + 2 x
-2x2 + x - 1
-2 x 2 – 2 x - 2
3x + 1
Таким образом 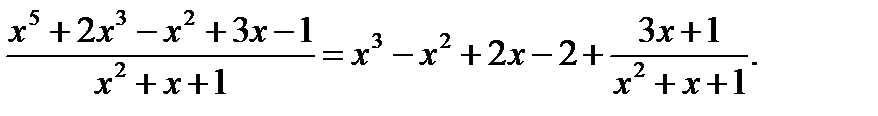



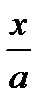 =
= 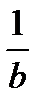 d b x =
d b x = 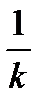 d(kx + b) = dx.
d(kx + b) = dx.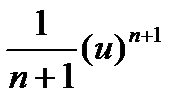 +C
+C






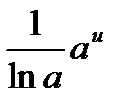 +C
+C
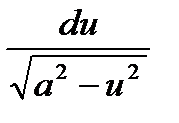
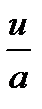 + C
+ C
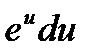

 + C
+ C
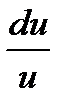
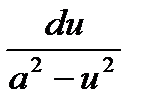
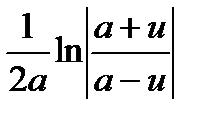 +C
+C
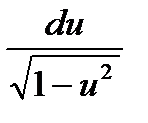
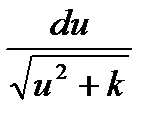
 | + C
| + C
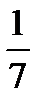 ∫ (2-7x)1/2d(2-7x) =
∫ (2-7x)1/2d(2-7x) =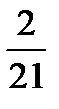 ∫d (2-7x)3/2 =
∫d (2-7x)3/2 = 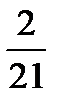 (2 -7x)3/2 + C.
(2 -7x)3/2 + C.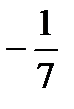 ∫ t1/2dt интеграл, который также является табличным.
∫ t1/2dt интеграл, который также является табличным.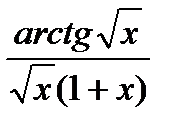 dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену
dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену 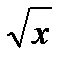 = t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫
= t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫  2tdt = 2∫
2tdt = 2∫ 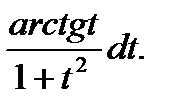 Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫
Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫ 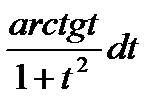 =
=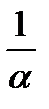 F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx =
F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx = 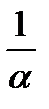 F(αx+β) + C.
F(αx+β) + C.

 =
= 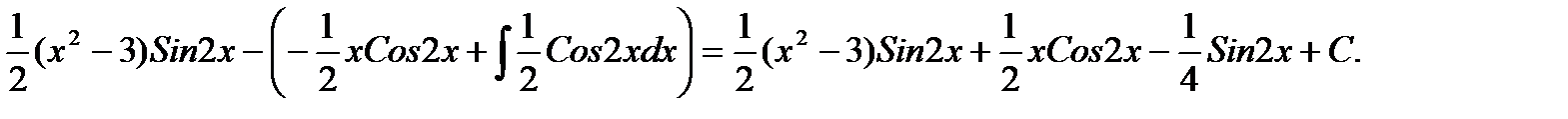
 = =x2arctgx – x +arctgx + C.
= =x2arctgx – x +arctgx + C.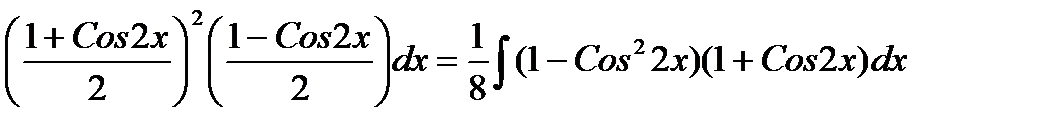 =
= 


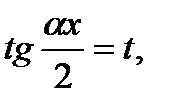 (6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =
(6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =  (7) Разрешим формулу (6) относительно независимой переменной -
(7) Разрешим формулу (6) относительно независимой переменной - 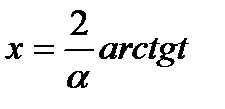 и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной
и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной  (8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
(8) Подставляя формулы (7), (8) в подынтегральное выражение, получим (9)
(9)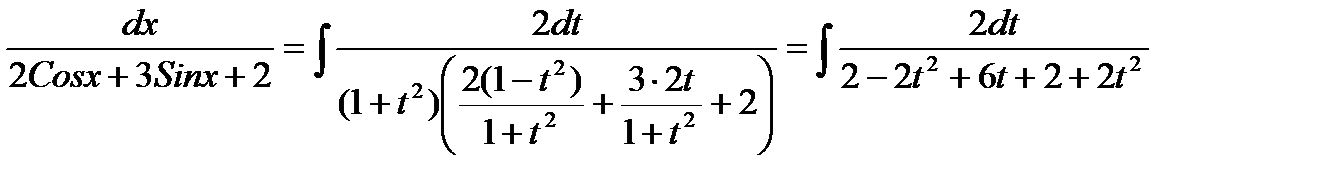 =
=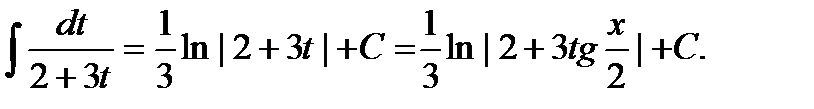
 (11)
(11)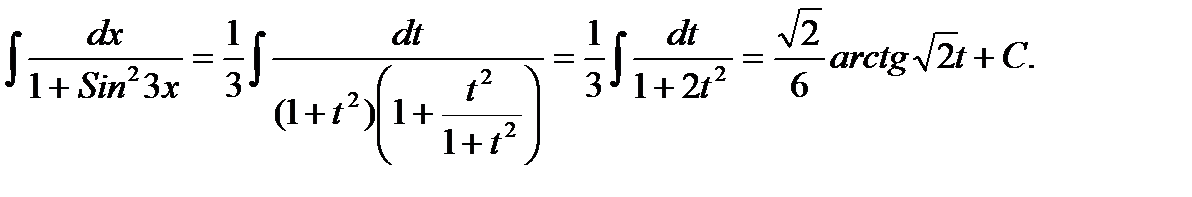
 гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то
гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то 

 как сумму многочлена и правильной дроби, разделив многочлены уголком:
как сумму многочлена и правильной дроби, разделив многочлены уголком: