

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Лекция 9.
Рассмотрим функцию двух переменных z = z(x;y). Если зафиксировать переменную  , то функция становится функцией одной переменной
, то функция становится функцией одной переменной  .
.
Определение. Частным дифференциалом по переменной x называется главная часть соответствующего частного приращения, пропорциональная приращению аргумента ∆ x.
Частные дифференциалы принято обозначать - dxz, dyz и т.д. Формула вычисления частных дифференциалов аналогична формуле вычисления дифференциала функции одной переменной, учитывая вычисление производной как частной. Так, для функции z = z(x;y) частные дифференциалы примут вид:
 (35)
(35)
Найдем частные дифференциалы примера 1:dxz=(2xy3+y2Cos(xy2))dx, dyz = (3x2y2 + 2xyCos(xy2))dy.
Отметим, что геометрически частные дифференциалы являются полученным в пересечении поверхности и плоскости закрепленной переменной.
Вообще говоря, полное приращение функции весьма сложно выражаются через приращения независимых переменных за исключением функции z = ax + by + c. Полное приращение линейной функции двух переменных, как легко видеть будет
∆z = a∆x + b∆y. Но оказывается, что для независимых переменных произвольной функции z = z(x;y) можно подобрать такие коэффициенты a и b, что выражение a∆x + b∆y хотя и не будет в точности равно ∆z, но будет отличаться от него на величину бесконечно малую более высокой малости, чем расстояние  между точками P(x;y) и P1(x+∆x;y+∆y). То есть полное приращение можно представить в виде
между точками P(x;y) и P1(x+∆x;y+∆y). То есть полное приращение можно представить в виде
∆z = a∆x + b∆y + α, (36)
|
|
причем 

Сумма a·∆x + b·∆y называется полным дифференциалом функции z = z (x; y) и
обозначается:
dz = a·dx + b·dy (37)
Как и прежде dx =∆x, dy = ∆y, и выражение (37) будем называть главной частью полного приращения функции. Нетрудно видеть, что разность между полным дифференциалом и полным приращением функции уменьшается при ρ→0.
Определение. Полным дифференциалом функции двух независимых переменных называется главная часть полного приращения функции, линейная относительно приращений аргументов.
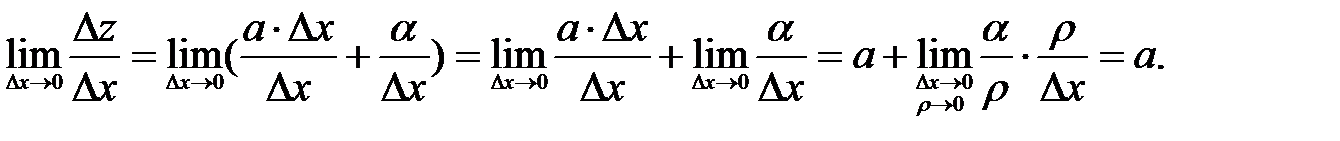
Итак,  Аналогично получим
Аналогично получим  Подставляя значения a и b в равенство (37), получим формулу вычисления полного дифференциала:
Подставляя значения a и b в равенство (37), получим формулу вычисления полного дифференциала:
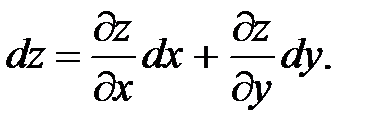 (38)
(38)
Таким образом, полный дифференциал функции 2-х переменных равен сумме произведений частных производных функции на соответствующие дифференциалы независимых переменных.
dz = (2xy3+y2Cos(xy2))dx + (3x2y2 + 2xyCos(xy2))dy.
Анализируя равенство (38), можно заключить: полный дифференциал функции 2-х переменных равен сумме ее частных дифференциалов: dz = dxz + dyz.
Замечание. Аналогичные формулировки о частных производных, дифференциалах и полном дифференциале можно сделать и для функции многих переменных u=u(x,y,z,..,t),
du = dxu + dyu + dzu + …………..+ dtu.
Пример. Найти полный дифференциал функции u = ln(xyz2 +x3 – y). Найдем частные производные функции: 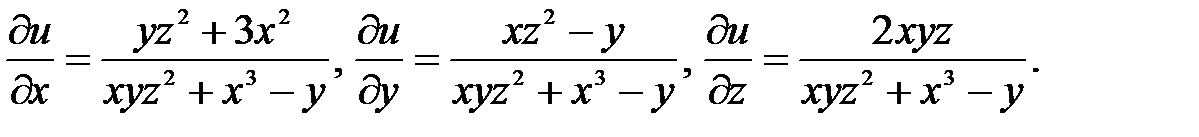 Теперь полный дифференциал функции
Теперь полный дифференциал функции
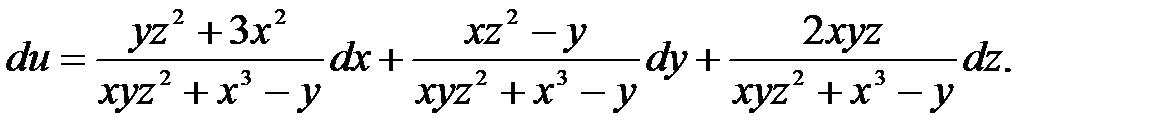
§19 Уравнение касательной плоскости к поверхности z = z(x;y).
Геометрический смысл полного дифференциала.
Пусть функция z =z(x;y) описывает поверхность S и дифференцируема в точке P(x0,y0). Рассмотрим сечения поверхности S плоскостями x = x0 и y = y0. К полученным плоским кривым в соответствующих плоскостях в точке M0(x0,y0,z0) проведем касательные M0Tx и M0Ty. Эти две пересекающиеся в точке кривые определяют плоскость, которая называется касательной, а точка M0 – точкой касани я. Найдем уравнение касательной плоскости. Так как касательные M0Tx и M0Ty лежат в касательной плоскости, то, подставляя уравнения касательной M0Tx:  и касательной M0Ty:
и касательной M0Ty:
|
|
 в уравнение касательной плоскости z – z0 = A(x – x0) + B(y – y0), найдем коэффициенты A, B. В результате подстановки находим
в уравнение касательной плоскости z – z0 = A(x – x0) + B(y – y0), найдем коэффициенты A, B. В результате подстановки находим 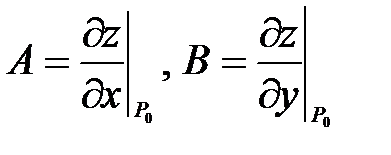 .
.
Таким образом, уравнение касательной плоскости к поверхности z=z(x;y) в точке M0 принимает вид:  (39)
(39)
Для достаточно близких точек P(x;y) к точке P0(x0;y0) разность значений аргументов заменим их приращениями: x-x0 = ∆x = dx, y – y0 = ∆y = dy. В этом случае правая часть выражения (39) является полным дифференциалом для функции z = z(x;y). Поэтому уравнение касательной плоскости можно записать в виде:  , где z0–аппликата точки касания, z – текущая аппликата касательной плоскости, а dz(x0;y0) - полный дифференциал в точке P0.
, где z0–аппликата точки касания, z – текущая аппликата касательной плоскости, а dz(x0;y0) - полный дифференциал в точке P0.
Таким образом, дифференциал функции z=z(x;y) в произвольной точке есть приращение точки касательной плоскости. В этом состоит геометрический смысл полного дифференциала.
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!