Неопределенный интеграл
Лекция 1.
§1 Определение неопределенного интеграла и его свойства.
Ранее изучалась задача: по заданной функции найти её производную. Поставим обратную задача: по заданной производной найти функцию. Для решения этой задачи введем понятие первообразной функции.
Первообразной некоторой заданной функции называется такая функция, производная которой равна заданной.
Пусть дана функция y = f(x). Тогда функция F(x) будет первообразной для f(x), если выполняется равенство
F’(x) = f(x) (1) или d F(x) = f’(x)dx (2)
Первообразная, являясь функцией, геометрически изображается кривой, называемой интегральной.
Неопределенный интеграл геометрически изображается совокупностью одинаковых интегральных кривых, сдвинутых по оси ординат.
Свойства неопределенного интеграла
Пусть выполняются равенства (1) или (2) и по определению неопределенного интеграла ∫ f(x)dx = F(x) + C. (3)
1. Производная неопределенного интеграла равна подынтегральной функции. Доказательство. Продифференцируем равенство (3): (∫ f(x)dx)’ = (F(x) + C)’. Учитывая свойства производной и равенство (1), получим
(∫ f(x)dx)’ = F’(x) = f(x).
Что и требовалось доказать.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению. Это свойство доказывается аналогично предыдущему. В результате получим d(∫ f(x)dx) = d(F(x) + C) = f(x)dx. Что и требовалось доказать.
Интеграл от дифференциала функции равен совокупности функций под дифференциалом.
Доказательство. Пусть совокупность первообразных некоторой функции будет F(x) + C = f(x) + C. По определению первообразной (формула (2)) имеем d(F(x)+C)=d(f(x)+C) = df(x). Следовательно, по второму свойству выражением под знаком интеграла является df(x). Таким образом, ∫ df(x) = (F(x)+C) =f(x) + C, что требовалось доказать.
Постоянный множитель можно выносить за знак интеграла
∫к f(x)dx = k∫ f(x)dx,
где k – постоянный множитель.
Действительно, продифференцируем обе части равенства (∫к f(x)dx)’=(k∫ f(x)dx)’;
(∫к f(x)dx))’ = k f(x); (k∫ f(x)dx)’ = k(∫ f(x)dx)’ = kf(x). Что и требовалось доказать.
Лекция 2.
§2 Интегрирование методом замены переменной (метод подстановки) и
методом по частям.
Метод замены переменной. Заключается в замене части подынтегральной функции (подынтегрального выражения) или аргумента сложной функции. Выбор замены следует производить таким образом, чтобы после замены подынтегральное выражение соответствовало выражениям табличных интегралов. Производя замену, необходимо все подынтегральные функции и дифференциал выразить через новую переменную. Нередко, признаком замены является наличие степеней с разницей в единицу. Особенно, если аргументом функции является высшая степень. Так, в примере 2 - ∫3x2ex3dx сделаем замену t = x3, dt = 3x2dx и интеграл принимает вид табличного ∫3x2ex3dx = ∫etdt. В третьем примере ∫ (2-7x)1/2dx заменим подкоренную функцию t =2-7x. Дифференцируя замену, получим dt = -7dx или dx = -dt/7. После подстановки получим ∫ (2-7x)1/2dx = - 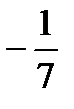 ∫ t1/2dt интеграл, который также является табличным.
∫ t1/2dt интеграл, который также является табличным.
Выбор замены представляется сложной процедурой и лучше удается при знании табличных интегралов. Во всяком случае, замене подлежат те функции, которые мешают интегралу быть табличным, или замена которых упрощают интегрируемую функцию. Например ∫ 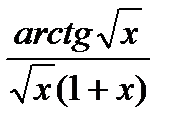 dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену
dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену 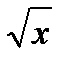 = t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫
= t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫ 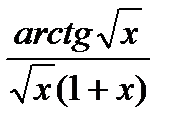 dx = ∫
dx = ∫  2tdt = 2∫
2tdt = 2∫ 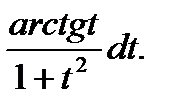 Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫
Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫ 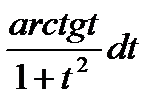 =
=
2∫tdt = t2 + C = arctg2t+ C.
В приведенных примерах использована замена вида u = φ(x). Покажем теперь применение замены вида x = g(u) на примере ∫Cos3 xdx. Представим функцию Cos3 x в виде Cos3 x = Cos2 x·Cosx = (1 – Sin2x)Cosx и произведем замену u = Sinx, du = Cos xdx. После подстановки получим:∫Cos3xdx =∫(1 – Sin2x)Cosxdx =∫(1 – u2)du=∫du-∫u2du=u-u3/3+C Обратную замену можно не производить, учитывая дальнейшее применение неопределенного интеграла при решении практических задач.
Замечание 1. Если функция f (x) имеет своей первоорбразной функцию F (x), то первоорбразной функции f (α x + β) будет функция 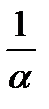 F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx =
F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx = 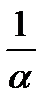 F(αx+β) + C.
F(αx+β) + C.
Замечание 2. Если числитель подынтегральной функции является производной знаменателя, то первообразная является логарифмом знаменателя, т.е. если f’(x)=φ(x), то 
Примеры. 
§3. Метод интегрирования по частям.
Метод основан на формуле вычисления дифференциала произведения двух функций u =u(x), v = v(x): d(u·v) = u·dv + v·du, u·dv = d(u·v) - v·du. Интегрируя обе части последнего равенства, получим
∫u·dv = ∫d(u·v) - ∫v·du
или ∫ u · dv = u · v - ∫ v · du (4)
Формула (4) носит название формулы интегрирования по частям. Интегрирование по частям состоит в том, что подынтегральное выражение f(x)dx представляется в виде произведения u·dv, выбирая в качестве u(x) такую функцию, дифференциал которой упрощает интеграл правой части (4). Аналогично - выражение dv интегрированием также упрощает интеграл правой части.
Во всяком случае, если подынтегральное выражение является произведением многочлена Pn(x) на дифференциалы вида eβx, Sinβx, Cosβx, то за u принимают многочлен Pn(x) и применяют формулу до тех пор, пока производная от многочлена не станет константой.
Пример. ∫(x2-3)·Cos2xdx=  =
= 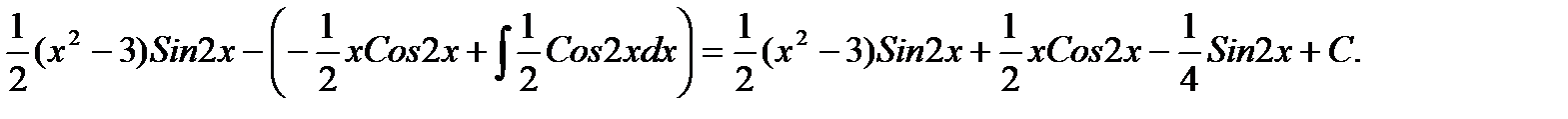
Если подынтегральное выражение включает одну из трансцендентных функций lnx, arccos(αx), arcsin(αx), arctgβx, то их надо принимать за u, так как производные от них более простые функции.
Пример. 2 ∫xarctgxdx =  = =x2arctgx – x +arctgx + C.
= =x2arctgx – x +arctgx + C.
Во всяком случае, признаком применения формулы интегрирования по частям может служить различная классификация функций, входящих в подынтегральную функцию. Например: многочлен и показательная; многочлен и трансцендентная.
§4. Интегрирование тригонометрических функций вида f(x)=Sinnx·Cosmx.
Универсальная подстановка.
Пусть подынтегральная функция f (x)= Sinnx · Cosmx, где показатели степеней – целые положительные числа. Интегрируя такие функции, следует различать два случая. 1. Показатели степеней четные, т.е. n = 2k, m = 2r. В этом случае порядок степеней следует понизить, применив формулы:
Sin2x = (1 – Cos2x)/2; Cos2x = (1 + Cos2x)/2 (5) преобразования подынтегральная функция будет представлять собой сумму произведений и, если показатели сомножителей вновь будут четными, то операцию понижения степени следует повторить. 2. Второй случай – один (оба) показатель (ля) нечетные. Тогда сомножитель с нечетным показателем (когда оба, неважно с каким) представляют в виде произведения одного сомножителя и сомножителя четной степени. Так, если например n = 2k + 1, то Sin2k+1x = Sin2kx·Sinx, после чего производят замену t = Cosx. Учитывая, что dt = dCosx = -Sinxdx, Sin2x = 1 – Cos2x = 1 – t2, подынтегральная функция станет многочленом переменной t. Действия аналогичны, если Cosmx = Cos2r+1x=Cos2rx·Cosx
Примеры. ∫Cos4xSin2xdx = ∫ 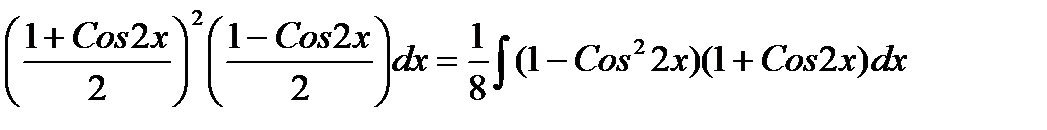 =
= 
= 
∫Cos3xSin2xdx = ∫Cos2xSin2xCosxdx = ∫(1-Sin2x)Sin2xdSinx = 
Интегралы ∫R(Sinαx;Cosαx)dx, подынтегральная функция которых является рациональной функцией переменных Sinαx и Cosαx сводятся к интегрированию рациональной функции одной переменной заменой, называемой универсальной, -
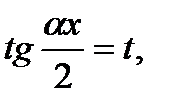 (6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =
(6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =  (7) Разрешим формулу (6) относительно независимой переменной -
(7) Разрешим формулу (6) относительно независимой переменной - 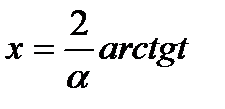 и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной
и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной  (8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
(8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
∫R(Sinαx;Cosαx)dx =  (9)
(9)
Пример. ∫ 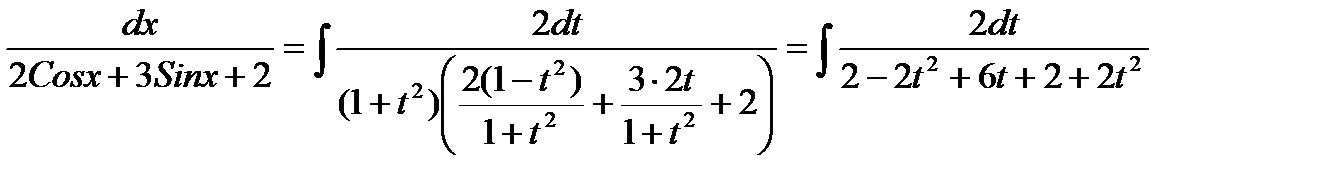 =
=
= 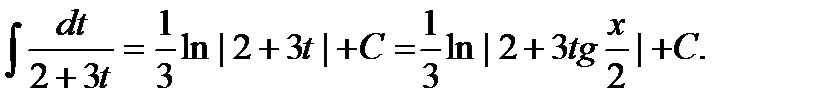
В случае, когда функции Sinαx и Cosαx входят в рациональную функцию R(Sinαx;Cosαx) в четных степенях, то применят замену
t = tgαx, (10)
учитывая, что  (11)
(11)
Пример. 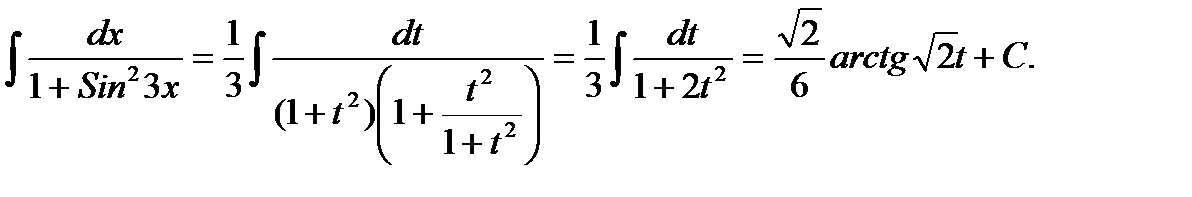
Лекция 3
§5. Интегрирование дробно-рациональных функций.
Определение. Отношение двух многочленов одной переменной называется дробно-рациональной функцией или рациональной дробью.
Определение. Дробь называется неправильной, если порядок многочлена числителя больше или равен порядка многочлена знаменателя, и правильной, если меньше.
Теорема. Любую неправильную дробь можно представить в виде суммы многочлена и правильной дроби, т.е. если f(x) =  гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то
гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то 
Пусть Pn(x) = x5 + 2x3 – x2 + 3x – 1; Qm(x) = x2 + x + 1. Представим неправильную дробь

 как сумму многочлена и правильной дроби, разделив многочлены уголком:
как сумму многочлена и правильной дроби, разделив многочлены уголком:
x5 +0x4 + 2x3 – x2 + 3x – 1| x 2 + x + 1
x 5 +0 x 4 + x 3 x3 – x2 +2x - 2
-x4 + x3 – x2
- x 4 - x 3 - x 2
2x3 - 0x2 + 3x
2 x 3 + 2 x 2 + 2 x
-2x2 + x - 1
-2 x 2 – 2 x - 2
3x + 1
Таким образом 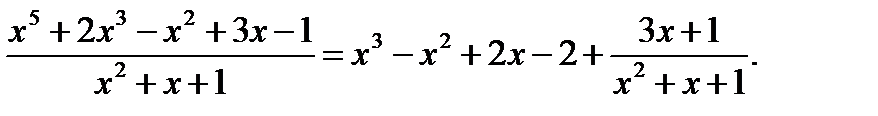
Лекция 4.
§6. Интегрирование некоторых иррациональных функций.
Рассмотрим интегрирование функции, рациональной относительно переменной и различных радикалов из неё, т.е. R(x, 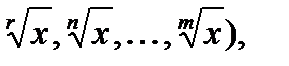 Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например.
Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например. 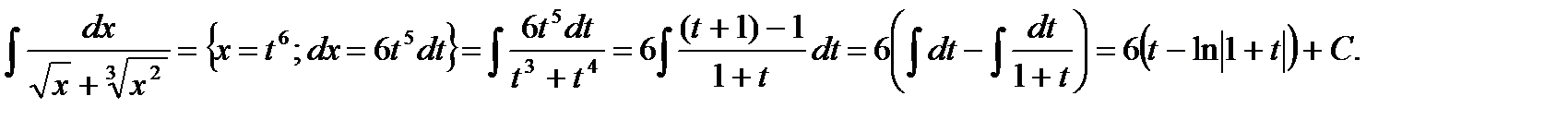
Практически ничего не меняется, если подкоренное выражение есть одна и та же дробно линейная функция 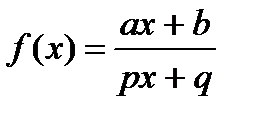 , особенно, если p=0, q =1.
, особенно, если p=0, q =1.
Рассмотрим несколько интегралов, зависящих от иррационального выражения 
1.Если интеграл имеет вид  , то преобразуя радикал к виду
, то преобразуя радикал к виду 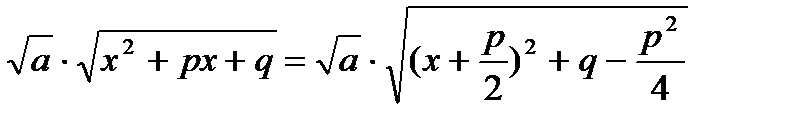 и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например
и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например 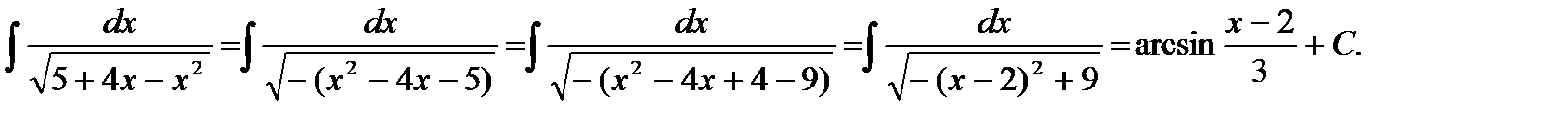
2. Интеграл вида 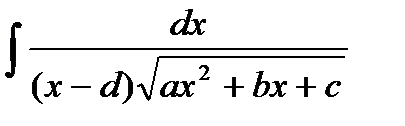 заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
3. Интегралы 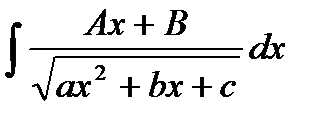 представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
4. Интегралы с функциями вида а) 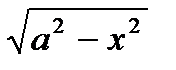 , б)
, б) 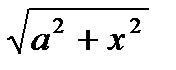 , в)
, в) 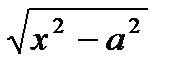 соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
Примеры.1.  =
= 
Нередко функции вида б), в) преобразуют используя замены гиперболическими функциями x = a·sht, x = a·cht, учитывая соотношения ch2t – sh2t = 1; 2ch2t = 1 + ch2t; 2sh2t= ch2t – 1. Так, 2. 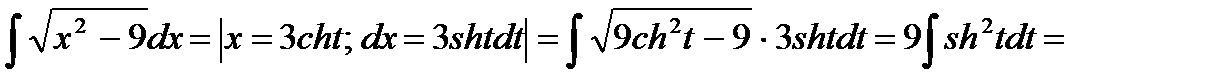
3. 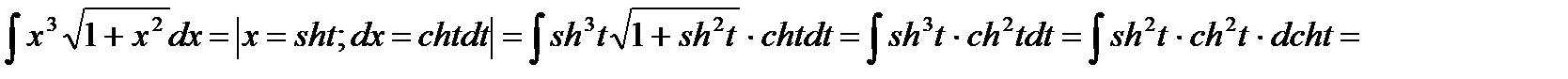 =
= 
Интегралы вида  заменами функций одной переменной сводятся к интегралам от рациональных функций
заменами функций одной переменной сводятся к интегралам от рациональных функций  Например
Например 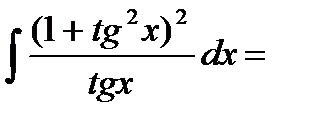

Определенный интеграл.
§7. Задача о вычислении площади криволинейной трапеции.
Определение. Фигура, ограниченная тремя прямыми, две из которых перпендикулярны третьей, и некоторой кривой, называется криволинейной трапецией.
Поставим задачу вычисления площади такой трапеции, ибо ни одна из формул евклидовой геометрии не может быть применена. Для этого введем декартову систему координат так, что ось ординат будет параллельна двум прямым, а ось абсцисс совпадает с третьей. Пусть кривая в заданной системе описывается функцией y= f(x), а трапеция
Для того чтобы представилась возможность применить известные формулы вычисления площади разобьем произвольным образом отрезок [a,b] на n частей (рис.1а). Каждую точку разбиения обозначим так, что x
0 = a, x
n = b. Рассмотрим «i» отрезок (рис1б), называемый элементом разбиения, длина которого ∆x
i = x
i – x
i-1 (i=1,2,3,……,n). Внутри каждого элемента разбиения выберем произвольную точку M
i(φ
i y
i = f(φ
i)) и заменим каждую криволинейную трапецию на отрезках ∆x
i прямоугольниками с высотами f(φ
i). В силу малости отрезков разбиения ∆x
i площадь каждого такого прямоугольника мало отличается по величине от криволинейной трапеции на каждом отрезке. Таким образом, величина площади на каждом элементе будет – ∆S
i = f(φ
i)· ∆x
i. Сумма всех элементарных площадей
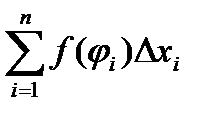
, называемая
интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
S =  (13)
(13)
Итак, площадь криволинейной трапеции равна пределу интегральной суммы при бесконечном увеличении числа разбиений.
§8 Определенный интеграл. Теорема существования.
Рассмотрим последовательность действий составления предела вида (13), отвлекаясь от физического смысла переменных и их обозначений –
1.отрезок [a,b], в котором задана непрерывная функция f(x), разбивается на n частей точками xi (i = 0,1,2,3,……,n), причем x0 = a<x1<x2<…..<xn-1<xn = b;
2.значение функции f(µi) в произвольно выбранной точке µiϵ [xi-1; xi]каждого элемента разбиения умножается на длину элемента ∆xi = xi – xi-1;
3.берется сумма всех таких произведений ln= f(µ1) ∆xi1+ f(µ2) ∆x2+…+ f(µn) ∆xn =
4.находится предел интегральной суммы (14) при стремлении к нулю максимальной длины элемента разбиения и, следовательно, при увеличении числа элементов разбиения, т.е. при n→∞:
I = 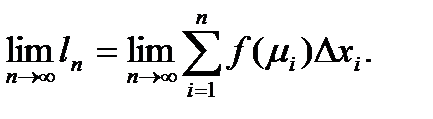 (15)
(15)
Предел (15) принято называть определенным интегралом или интегралом от функции f(x) в пределах от a до b и обозначается:
I = 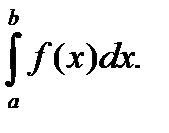 (16)
(16)
Ясно, что
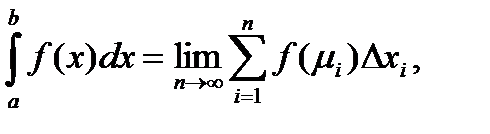
где f(x) называется подынтегральной функцией, f(x)dx - подынтегральным выражением, a,b – пределами интегрирования.
Определение. Определенным интегралом называется предел интегральной суммы (15) при увеличении числа элементов разбиения и стремлении к нулю наибольшего элемента разбиения, если он существует и не зависит от способа разбиения отрезка [ a, b ] выбора точки внутри каждого элемента разбиения.
Вообще говоря, интегральные суммы могут значительно отличаться друг от друга в зависимости от способа разбиения. Однако, для непрерывных функций это различие стирается при увеличении числа разбиений и стремлении максимальной длины элемента разбиения к нулю.
Теорема. Определенный интеграл существует, если подынтегральная функция непрерывна на множестве точек отрезка интегрирования [ a, b ].
Лекция 5.
§9. Свойства определенного интеграла. Теорема о среднем.
Учитывая определение определенного интеграла как предела интегральной суммы, перечислим без доказательства те свойства интеграла, которые доказываются с помощью свойств предела функции:
1.постоянный множитель можно выносить из под знака интеграла –
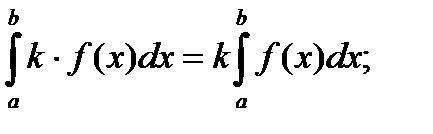
2. интеграл от суммы функций равен сумме интегралов от каждой функции –
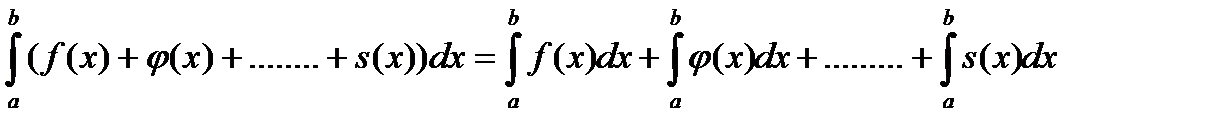
3. если отрезок интегрирования разбит на два участка, то интеграл от функции на отрезке интегрирования равен сумме интегралов от функции на обоих участках, т.е. если [a,b] = [a,c]+[c,b], то  ;
;
4. если f(x) ≥ 0 на отрезке [a,b], то и 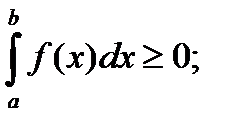
5. если f(x) ≥ φ(x) на [a,b], то и 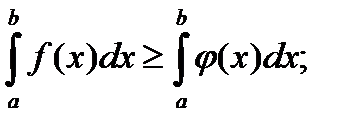
6. если поменять местами пределы интегрирования, то интеграл поменяет знак –
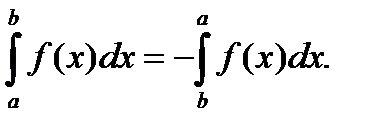
Доказательство этого свойства следует из изменения направления отсчета от b к a, когда xi < xi-1.
Теорема о среднем. Если подынтегральная функция непрерывна [ a, b ], то внутри отрезка найдется такая точка x = c, что выполняется равенство
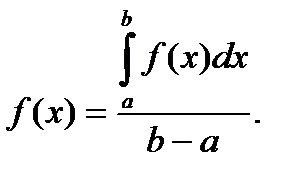 (17)
(17)
Доказательство. Так как функция непрерывна на отрезке, то по свойству функций непрарывных на отрезке она принимает свое нименьшее и наибольшее значение, т.е. она ограничена снизу и сверху. Пусть наименьшее m, а M наибольшее значения функции. Таким образом, выполняется неравенство
m ≤ f(x) ≤ M. (18)
Проинтегрируем неравество и, учитывая свойство 5, получим
m(b-a) ≤  ≤ M(b-a) (19)
≤ M(b-a) (19)
или m ≤  ≤ M.
≤ M.
Из свойств функций непрерывных на отрезки функция принимает все свои промежуточные значения и, следовательно, найдется точка cϵ[a.b], такая, что выполняется равенство (17).
§10. Теорема о производной определенного интеграла по переменному верхнему пределу.
Теорема. Производная от интеграла по переменному верхнему пределу равна подынтегральной функции
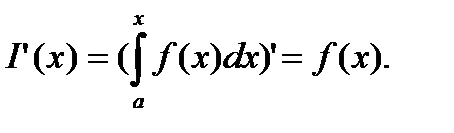 (20)
(20)
Доказательство. Из решения задачи отыскания площади криволинейной трапеции можно сказать, что геометрическим смыслом определенного интеграла является площадь и, следовательно, интеграл можно рассматривать как функции верхнего предела. Дадим приращение ∆x верхнему пределу и найдем приращение функции ∆I = I(x +∆x)-I(x) –
∆I = 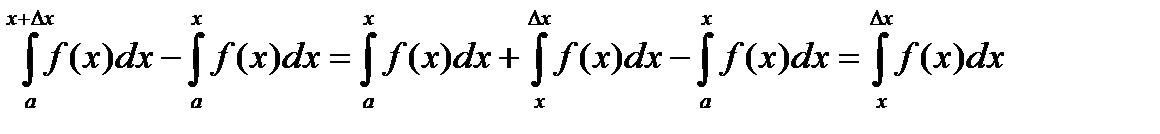 (21)
(21)
В выражении (21) первый интеграл представлен в виде суммы двух в соответствии со свойством 3 §9. Преобразуем последний интеграл, используя теорему о среднем –

где  . Очевидно, что при стремлении приращения аргумента к нулю
. Очевидно, что при стремлении приращения аргумента к нулю  . По определению производной имеем
. По определению производной имеем
I’(x) = 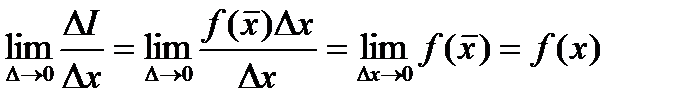
Теорема доказана.
Ее результат позволяет утверждать, что определенный интеграл с переменным верхним пределом есть первообразная подынтегральной функции. А это означает, что вычисление определенного интеграла можно произвести без вычисления предела.
§11. Формула Ньютона-Лейбница.
Теорема. Значение определенного интеграла равно разности значений любой первообразной подынтегральной функции, взятые при верхнем и нижнем пределах интеграла:
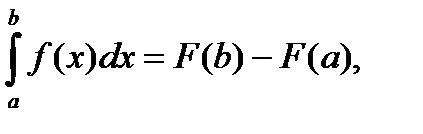 где F’(x) = f(x) (22)
где F’(x) = f(x) (22)
Равенство (22) называется формулой Ньютона – Лейбница.
Доказательство. Рассмотрим функцию
 , которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
, которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
I(a) = F(a) + C =  = 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
= 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
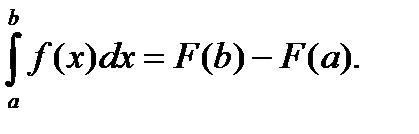
Теорема доказана.
Правую часть формулы Ньютона – Лейбница принято записывать в виде 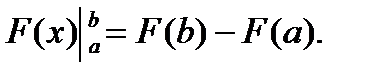
Примеры. Вычислить. 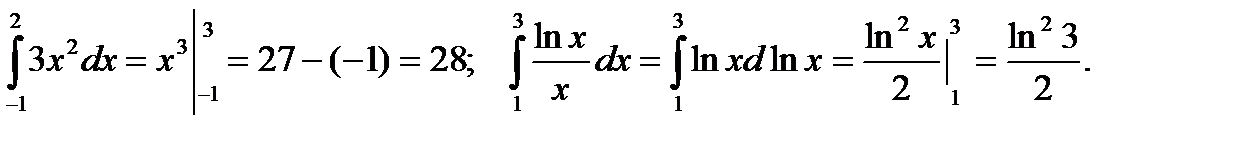
Если подынтегральная функция четная и пределы интегрирования симметричны относительно начала координат, то интеграл удваивается, а нижний предел принимается равным нулю.
Вычислить. 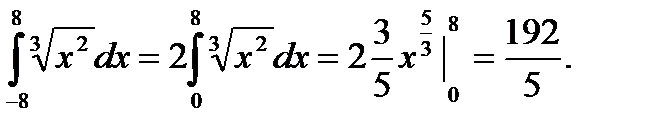
Интегрирование по частям в определенном интеграле производится по той же формуле что и в неопределенном интеграле, но с подстановкой пределов в слагаемые правой части:
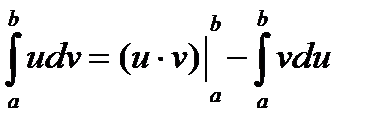 (23)
(23)
Пример.Вычислить. 
Правило замены переменной (подстановки) сводится к следующему: если в интервале [ c, d ] функции x =φ(u), φ’(u), f [φ(u)] непрерывны и φ(c) = a, φ(d) = b, то
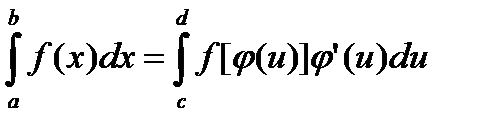 (24)
(24)
Из формулы (24) следует, что, производя замену переменной
x = φ(u), (25)
следует также заменить дифференциал dx, дифференцируя равенство (25) и заменить пределы интегрирования, вновь используя равенство (25) непосредственно или выразив u через x: u= ψ(x). Последнюю операцию лучше производить, используя табличную форму вида:
Пример. 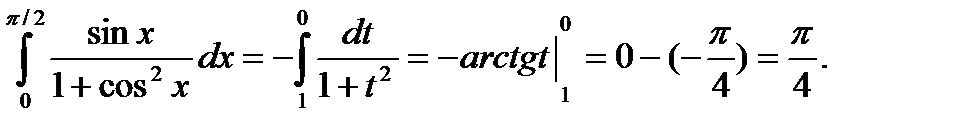
В примере произвели замену cosx = t, dt = -sinxdx
Лекция 8
Лекция 10
§20 Производные сложных функций многих переменных
Пусть дана сложная функция z=z(x;y), аргументы которой в свою очередь являются функциями одной переменной – x = x(t), y = =y(t). Требуется вычислить производную функции z=z(x;y) по независимой переменной t.
Найдем дифференциал функции 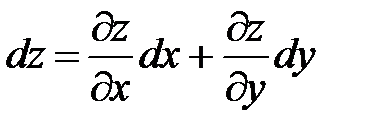 и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
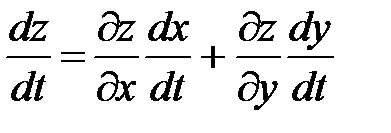 (41)
(41)
Пример. Вычислить производную функции z = sin(xy), если x = 2t, y = 3t3. Найдем частные производные функции z по x и y, и производные промежуточных аргументов x, y по t: 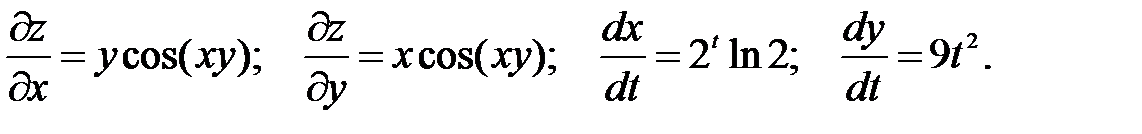 Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу -
Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу - 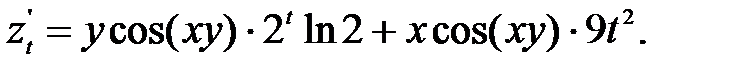
Пусть сложная функция z=z(x;y) является функцией многих независимых переменных, в частности 2-х – x = x(u,v), y = y(u,v). Требуется найти частные производные функции по независимым переменным 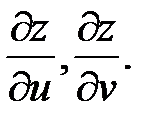 Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
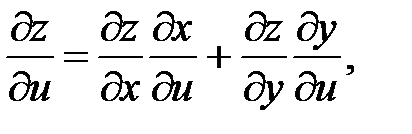 (42)
(42)
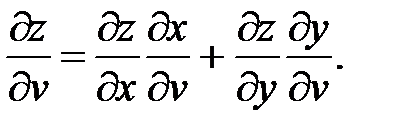 (43)
(43)
Анализируя формулы (41,42,43), можно сформулировать правило вычисления производных сложных функций многих переменных по независимой переменной –
Производная сложной функции по независимой переменной равна сумме произведений частных производных функции по промежуточным аргументам и производных соответствующих промежуточных аргументов по независимой переменной.
Пример. Вычислить производные функции s = x2y – (xyz)3/2 по переменной u и v, если x = u3 – v3, y = 2uv, z = vsinu.
Решение. Здесь x, y, z - промежуточные аргументы, u, v - независимые переменные (аргументы). Вычислим производные функции s по x, y, z –
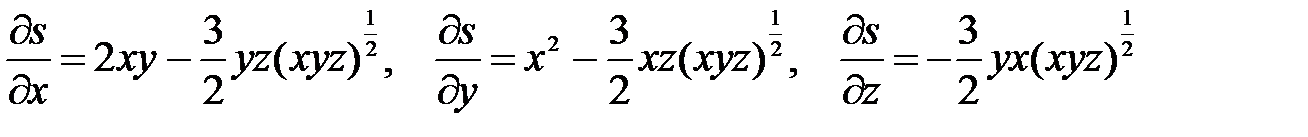 Теперь найдем производные промежуточных переменных по независимым u, v:
Теперь найдем производные промежуточных переменных по независимым u, v:
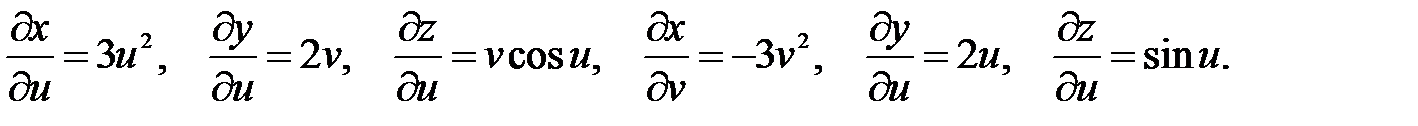 Применяя правило вычисления производных сложных функций, получим:
Применяя правило вычисления производных сложных функций, получим:
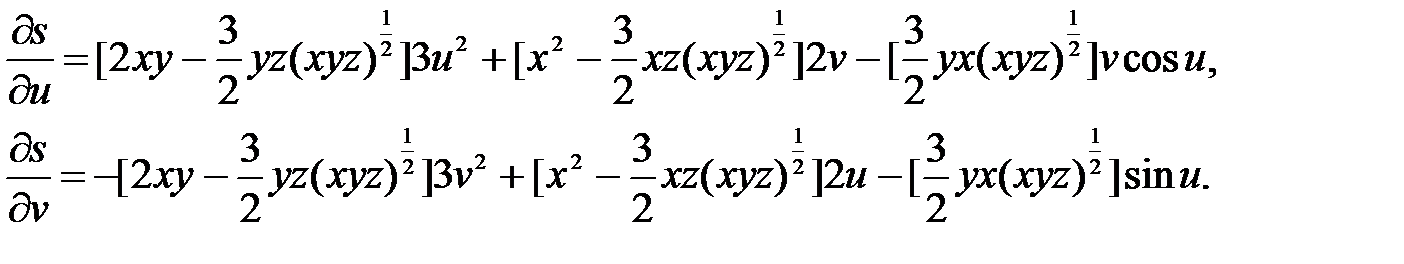
Пусть задана функция y = y(x) в неявном виде –
F(x, y(x)) = 0. (44)
Найдем производную по независимой переменной, продифференцировав равенство (44), учитывая, что левая часть есть сложная функция. Поэтому дифференцировать ее надо по выше сформулированному правилу: 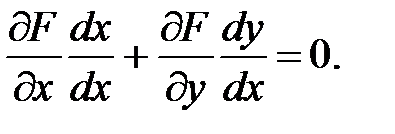 Разрешая равенство относительно y’, получим
Разрешая равенство относительно y’, получим 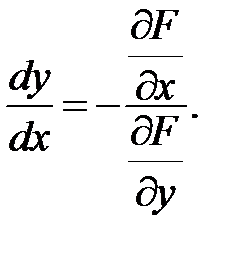 (45)
(45)
Если задана функция z=z(x;y) в неявной форме F(x, y, z(x,y)) = 0, то вычисляя производную функции многих переменных по переменной, получим 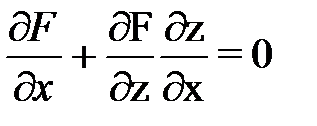 . Или
. Или
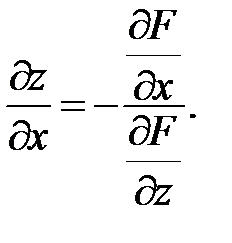 (46)
(46)
Аналогично рассуждая, получим производную по переменной y:
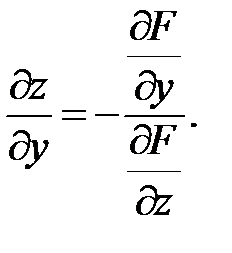 (47)
(47)
Пример. Найти производные функции z=z(x;y): z2y + x – arct(z-x) = 0. Найдем частные производные по переменным x, y, z функции F(x,y,z) = z2y + x – arct(z-x): 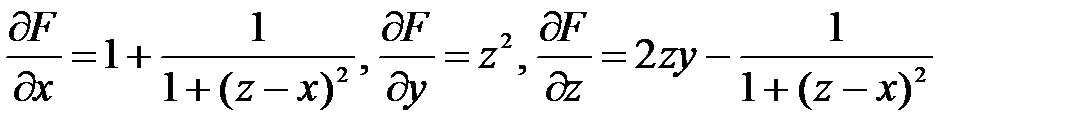 . Подставим в (46,47) и получим:
. Подставим в (46,47) и получим: 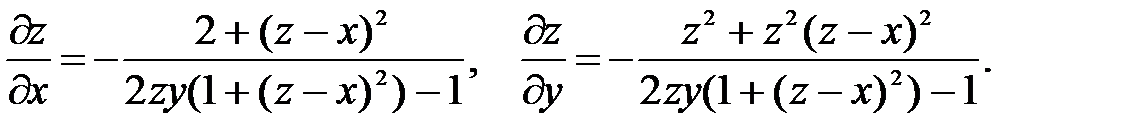
§21 Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана уравнением F(x,y,z) = 0. Требуется написать уравнение касательной плоскости в заданной точке M0(x0,y0,z0).
Известно [§19 (39)], что уравнение касательной плоскости к поверхности z =z(x,y) имеет вид: 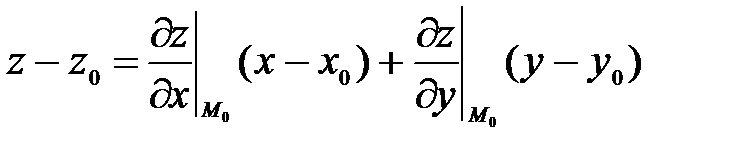 . А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:
. А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:  или
или
 (48)
(48)
Из аналитической геометрии известно, что уравнение плоскости через заданную точку есть скалярное произведение нормального вектора к плоскости 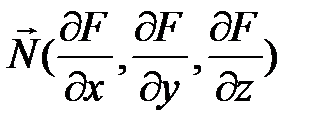 и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
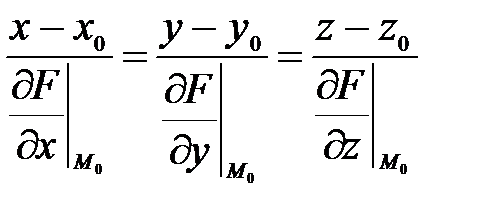 (49)
(49)
Пример. Написать уравнение касательной плоскости к поверхности x2 + y2 + z2=56,
параллельной плоскости 2x – y + 3z + 7 = 0.
Решение. Для написания уравнения касательной плоскости к поверхности следует найти координаты точки, принадлежащей поверхности. По условию координаты нормального вектора касательной плоскости должны быть пропорциональны координатам нормали заданной плоскости.
Найдем частные производные функции F(x,y,z) = x2 + y2 + z2-14 = 0 и удовлетворим условиям пропорциональности их соответствующим коэффициентам заданной плоскости: 2x = 2ρ, 2y = -ρ, 2z = 3ρ.
Разрешая равенства относительно переменных и подставляя их в уравнение поверхности, найдем коэффициент пропорциональности, при котором точка будет принадлежать поверхности: ρ2 + ρ2/4 + 9 ρ2/4 = 56; ρ2 = 4; ρ = ± 4.
Таким образом таких точек будет две:M1(4,-2,6) и M2(-4,2,-6).
Итак, уравнения касательных плоскостей, параллельных заданной, будут иметь вид: 2(x – 4) – (y +2) + 3(z – 6) = 0 и 2(x + 4) – (y -2) + 3(z + 6) = 0.
Уравнения нормалей к поверхности в этих точках будут:
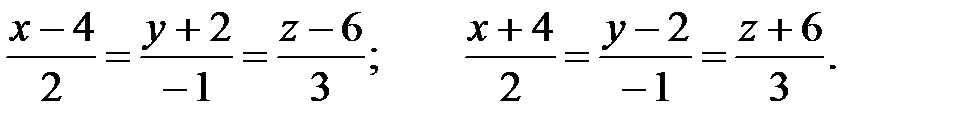
§22 Производные и дифференциалы высших порядков
функции двух переменных.
Очевидно, что частные производные функции z=z(x;y) также будут функциями двух переменных, так как фиксация переменных при вычислении частной производной произвольны. Поэтому от полученных частных производных можно в свою очередь найти частные производные.
Определение. Частные производные от частных производных функции z = z (x; y) называются частными производными второго порядка.
Частные производные второго порядка принято обозначать: 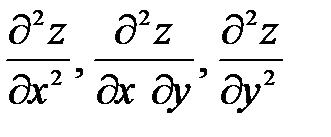 или
или
zxx, zxy, zyy. Следует заметить, что символы вторых производных неразделимы, т.е. символ  , как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных
, как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных 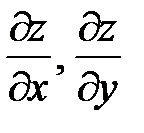 получаем четыре частные производные второго порядка
получаем четыре частные производные второго порядка 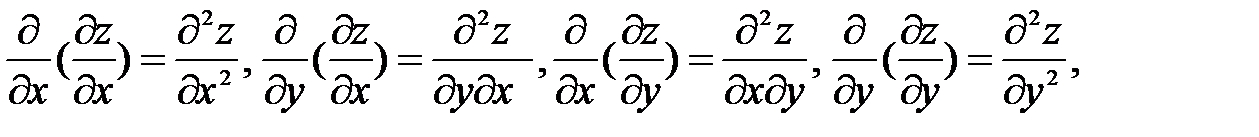 причем производные взятые по обеим переменным называются смешанными.
причем производные взятые по обеим переменным называются смешанными.
Теорема. Смешанные производные не зависят от порядка дифференцирования Покажем справедливость этой теоремы на примере дифференцирования функции z=cosxy.
zx = -ysin(xy), zyx = -sin(xy) – yxcos(xy),
zy = -xsin(xy), zxy = -sin(xy) - xycos(xy). Сравнивая вторые смешанные производные, видно что zyx = zxy.
Рассмотрим полный дифференциал функции z = z (x; y) (§18(38)) - 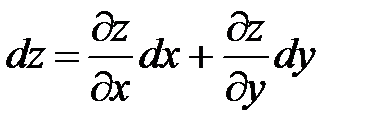 . Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
. Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
Определение. Вторым дифференциалом функции z = z (x; y) (дифференциалом второго порядка) называется дифференциал от первого дифференциала.
Вычисление второго дифференциала производится по тому же правилу что и первого. Найдем дифференциал второго порядка, который обозначается как d2z и читается де два зет:d2z = d(dz) = 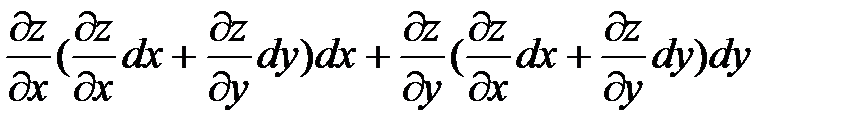 .Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим:
.Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим: 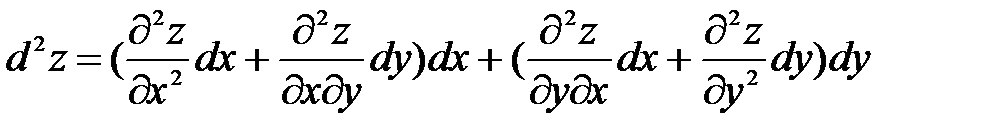 . Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
. Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
окончательно получим:
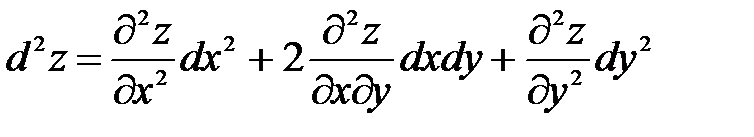 (50)
(50)
Дадим определения частных производных и дифференциалов N-го порядка.
Определение. Частной производной n –го порядка функции z = z (x; y) называется частная производная от частной производной n -1 порядка, т.е. 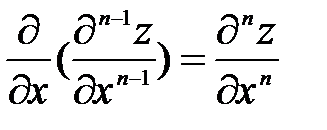 .
.
Теорема. Смешанная производная n -го порядка не зависит от порядка дифференцирования.

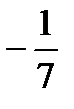 ∫ t1/2dt интеграл, который также является табличным.
∫ t1/2dt интеграл, который также является табличным.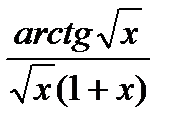 dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену
dx. Подсказкой в этом примере служат и радикал и функция арктангенс, которой нет среди подынтегральных функций табличных интегралов. Произведем сначала замену 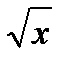 = t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫
= t, x = t2 и найдем дифференциал ее dx = 2tdt. В результате замены получим ∫  2tdt = 2∫
2tdt = 2∫ 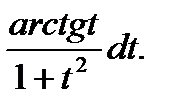 Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫
Если бы не было в числителе функции арктангенса, то интеграл стал бы табличным. Поэтому произведем замену u = arctgt; du = dt/(1+t2). В результате получим простой интеграл 2∫ 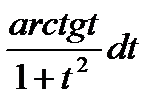 =
=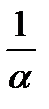 F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx =
F (α x +β), т.е. если ∫f(x)dx = F(x)+C, то ∫f(αx+β)dx = 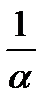 F(αx+β) + C.
F(αx+β) + C.

 =
= 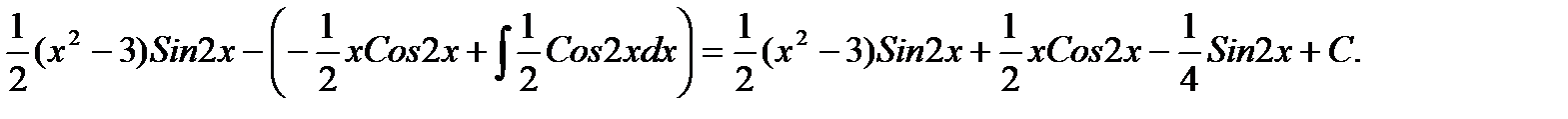
 = =x2arctgx – x +arctgx + C.
= =x2arctgx – x +arctgx + C.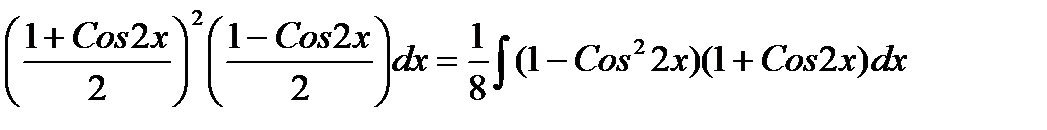 =
= 


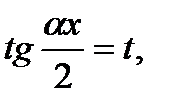 (6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =
(6) так как функции Sinαx и Cosαx выражаются через функцию тангенс половинного угла: Sinαx =  (7) Разрешим формулу (6) относительно независимой переменной -
(7) Разрешим формулу (6) относительно независимой переменной - 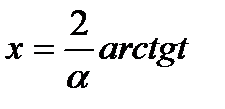 и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной
и продифференцируем полученное равенство. В результате найдем дифференциал независимой переменной  (8) Подставляя формулы (7), (8) в подынтегральное выражение, получим
(8) Подставляя формулы (7), (8) в подынтегральное выражение, получим (9)
(9)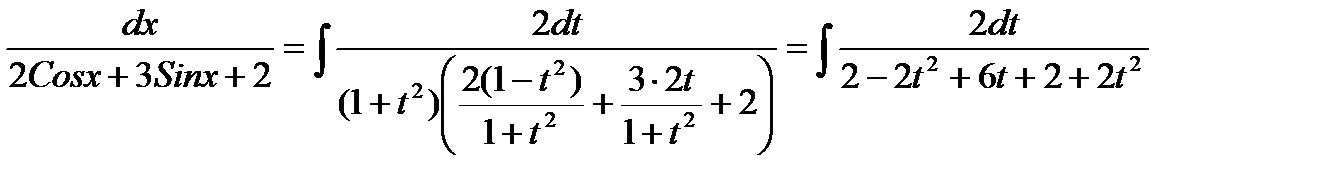 =
=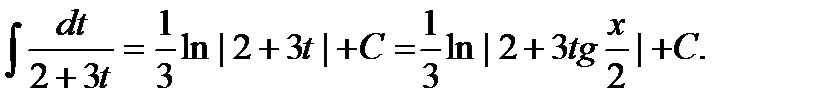
 (11)
(11)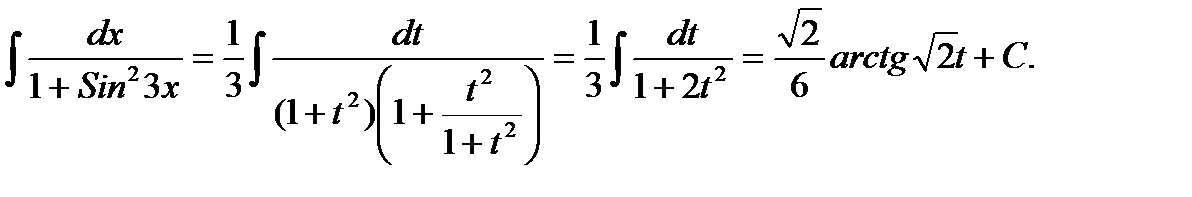
 гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то
гдеPn(x), Qm(x) многочлены соответственно порядка n и m (m ≤ n), то 

 как сумму многочлена и правильной дроби, разделив многочлены уголком:
как сумму многочлена и правильной дроби, разделив многочлены уголком: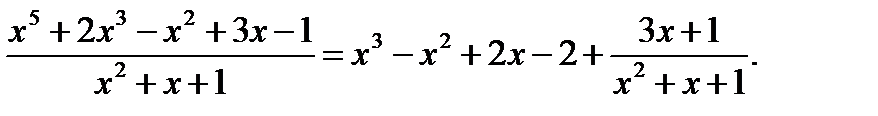
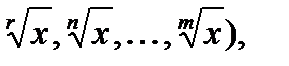 Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например.
Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например. 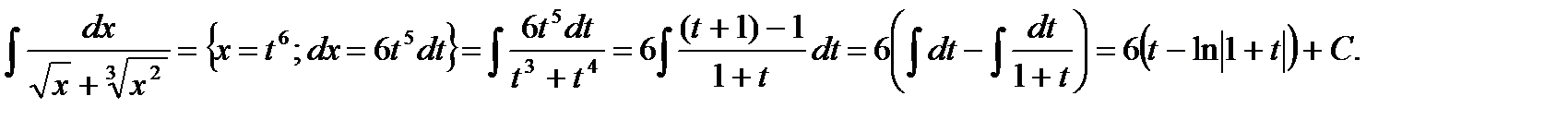
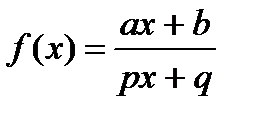 , особенно, если p=0, q =1.
, особенно, если p=0, q =1.
 , то преобразуя радикал к виду
, то преобразуя радикал к виду 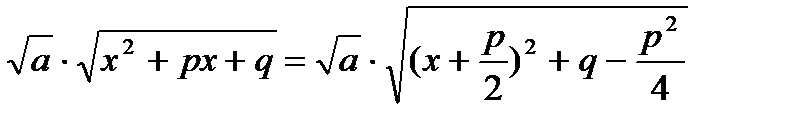 и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например
и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например 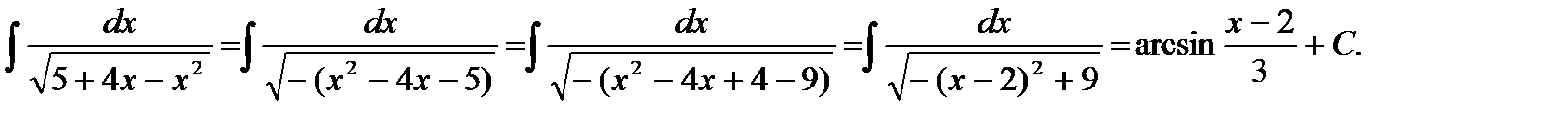
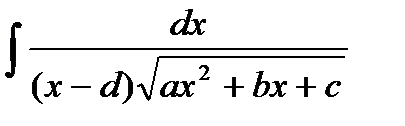 заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.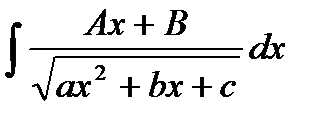 представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).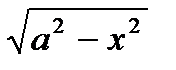 , б)
, б) 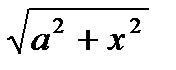 , в)
, в) 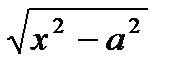 соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций. =
= 
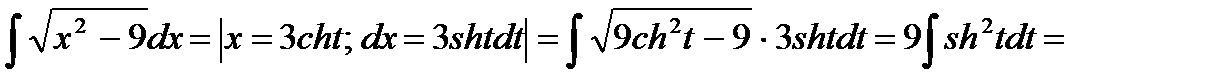
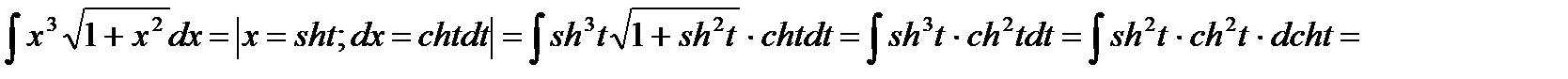 =
= 
 заменами функций одной переменной сводятся к интегралам от рациональных функций
заменами функций одной переменной сводятся к интегралам от рациональных функций  Например
Например 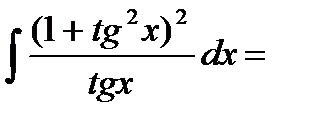

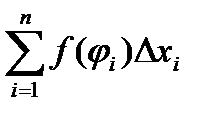 , называемая интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
, называемая интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
 (13)
(13)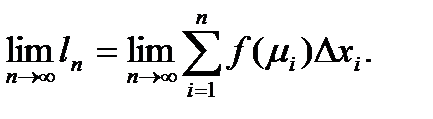 (15)
(15)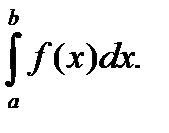 (16)
(16)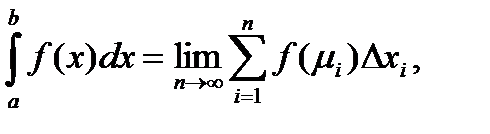
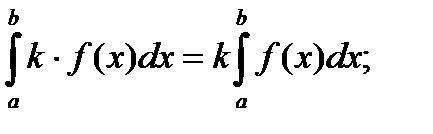
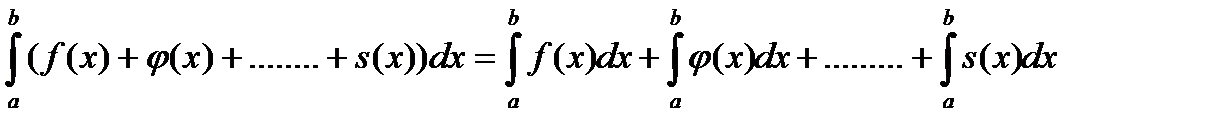
 ;
;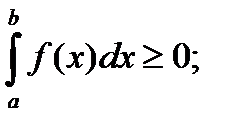
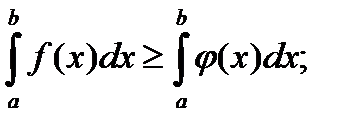
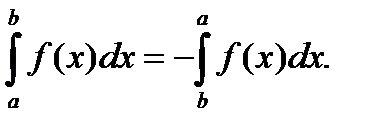
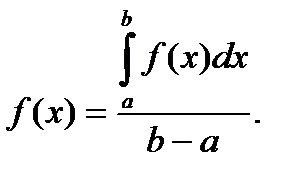 (17)
(17) ≤ M(b-a) (19)
≤ M(b-a) (19)  ≤ M.
≤ M. 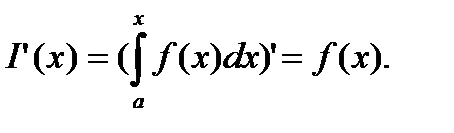 (20)
(20)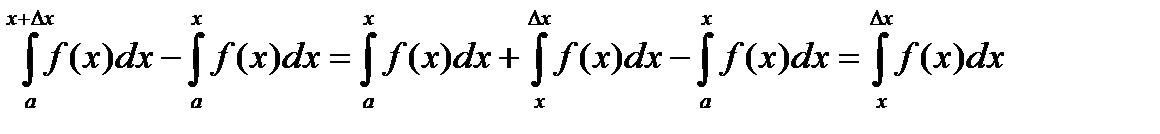 (21)
(21)
 . Очевидно, что при стремлении приращения аргумента к нулю
. Очевидно, что при стремлении приращения аргумента к нулю  . По определению производной имеем
. По определению производной имеем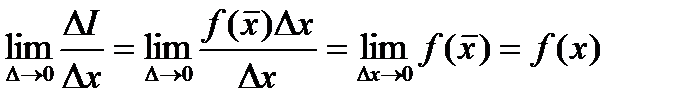
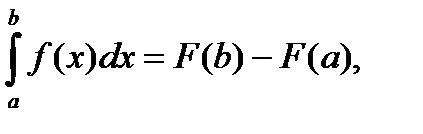 где F’(x) = f(x) (22)
где F’(x) = f(x) (22) , которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
, которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a. = 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
= 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим: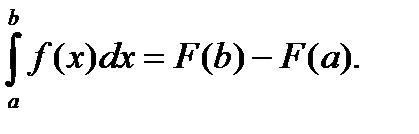
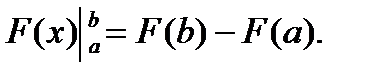
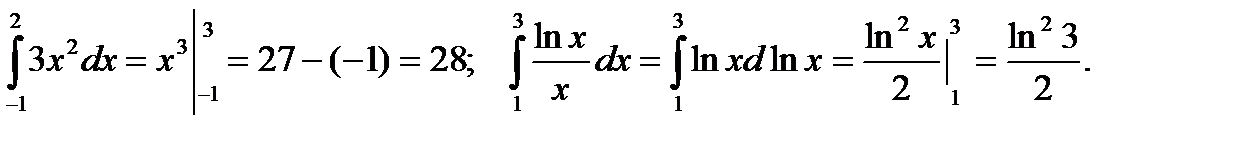
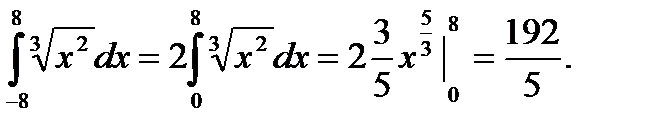
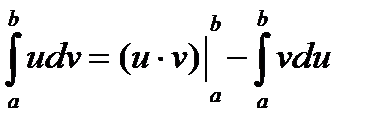 (23)
(23)
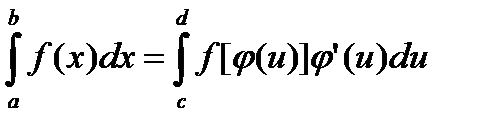 (24)
(24)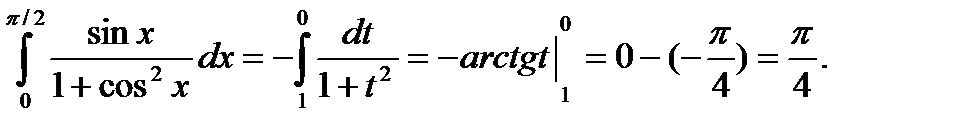
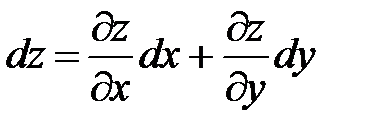 и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
и разделим обе части его на dt. В результате получим формулу вычисления сложной функции: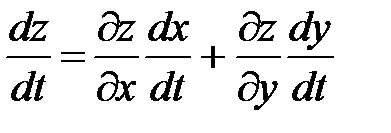 (41)
(41)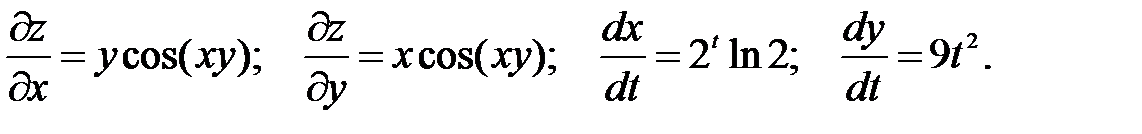 Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу -
Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу - 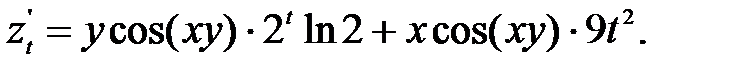
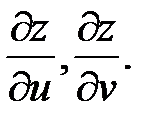 Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим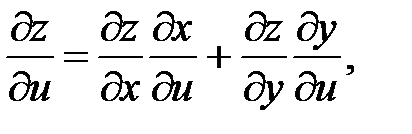 (42)
(42)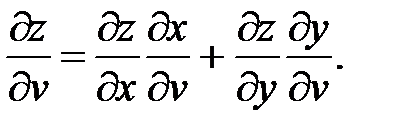 (43)
(43)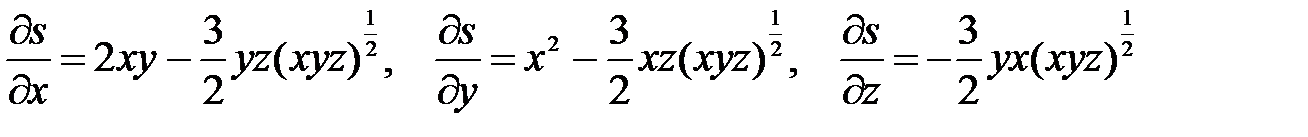 Теперь найдем производные промежуточных переменных по независимым u, v:
Теперь найдем производные промежуточных переменных по независимым u, v: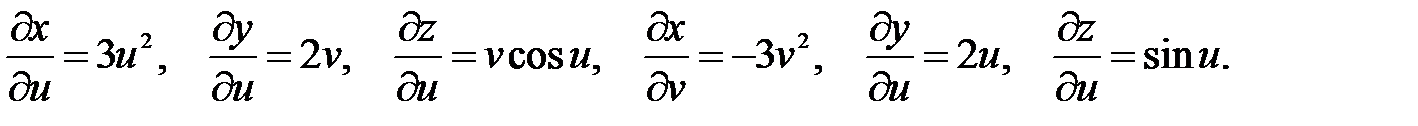 Применяя правило вычисления производных сложных функций, получим:
Применяя правило вычисления производных сложных функций, получим: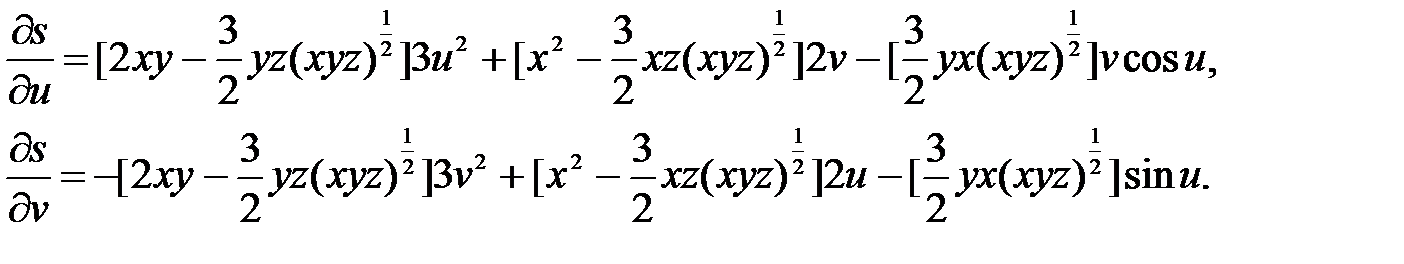
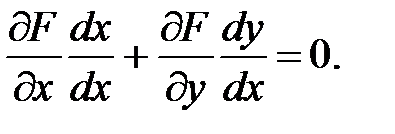 Разрешая равенство относительно y’, получим
Разрешая равенство относительно y’, получим 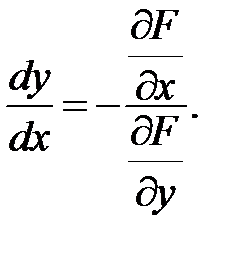 (45)
(45)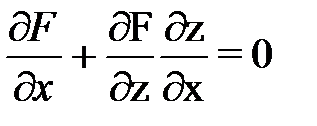 . Или
. Или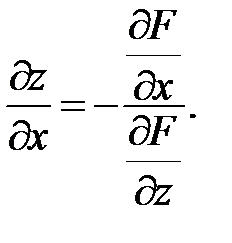 (46)
(46)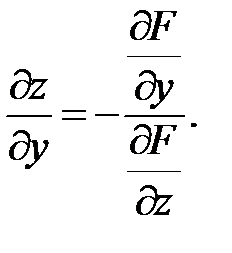 (47)
(47)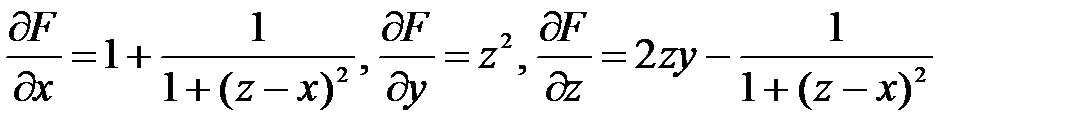 . Подставим в (46,47) и получим:
. Подставим в (46,47) и получим: 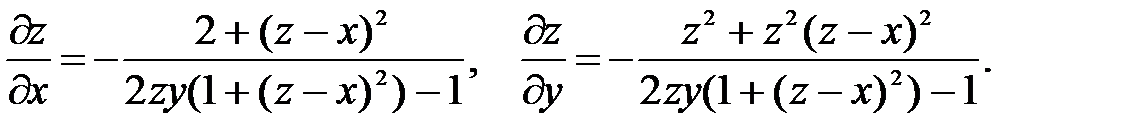
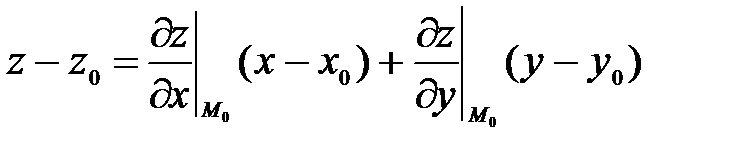 . А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:
. А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:  или
или (48)
(48)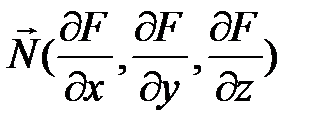 и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид: 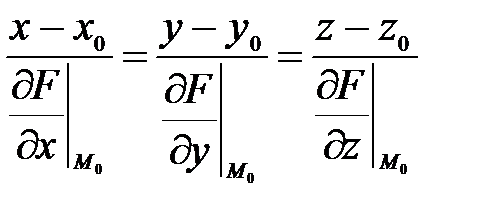 (49)
(49)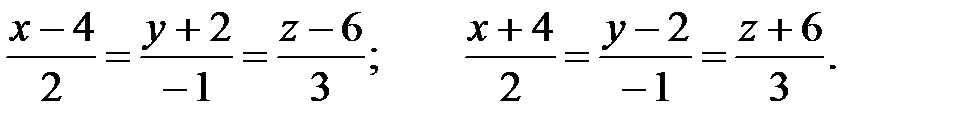
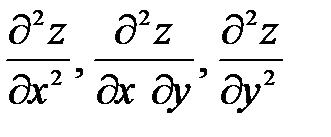 или
или , как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных
, как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных 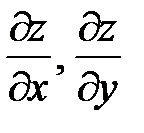 получаем четыре частные производные второго порядка
получаем четыре частные производные второго порядка 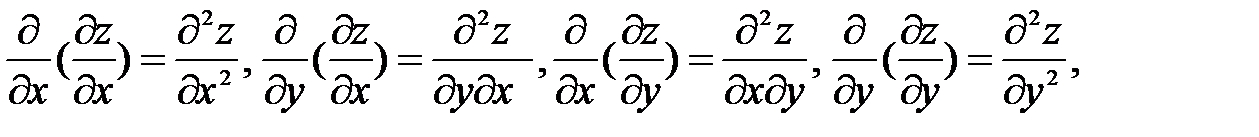 причем производные взятые по обеим переменным называются смешанными.
причем производные взятые по обеим переменным называются смешанными.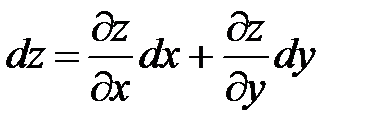 . Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
. Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.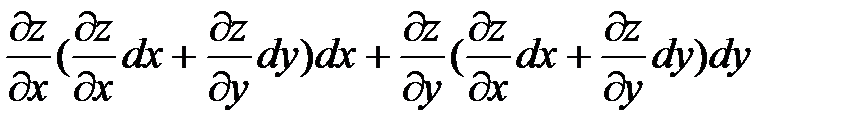 .Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим:
.Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим: 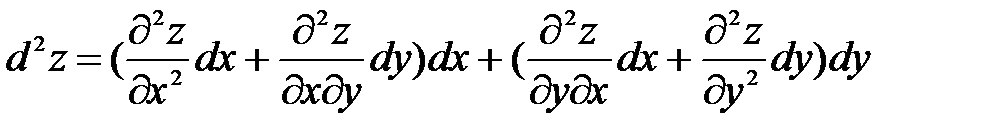 . Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
. Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований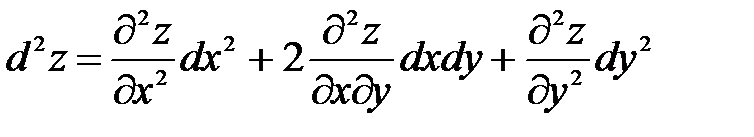 (50)
(50)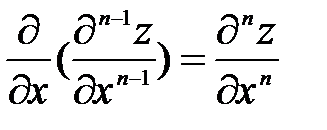 .
.