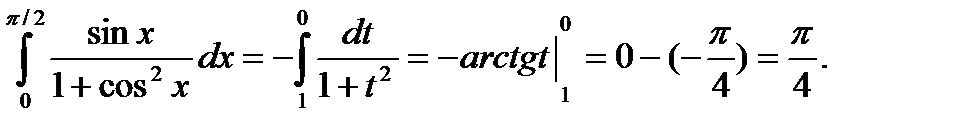Определение. Простыми дробями называются дроби вида: I.  II.
II.  III.
III. 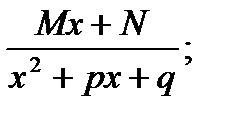 IY.
IY. 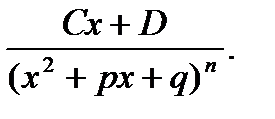 Здесь коэффициенты A,B,C,D,M,N - некоторые константы, a,b,p,q - заданные числа, x2+px+q – неразложимый трехчлен (p2-4q<0).
Здесь коэффициенты A,B,C,D,M,N - некоторые константы, a,b,p,q - заданные числа, x2+px+q – неразложимый трехчлен (p2-4q<0).
Интегралы от дробей первого и второго видов являются табличными. Интеграл от дроби третьего вида преобразованием знаменателя и числителя приводится к двум интегралам, первообразные подынтегральных функций которых известны. Покажем интегрирование такой дроби на примере.
 Представляем интеграл суммой интегралов. В первом - арифметическими операциями в числителе добиваемся выражения производной. Для
Представляем интеграл суммой интегралов. В первом - арифметическими операциями в числителе добиваемся выражения производной. Для
этого умножаем числитель на 2 и делим интеграл на 2 и добавляем минус и плюс 4.



Подставляя правую часть в предыдущее выражение, окончательно получим 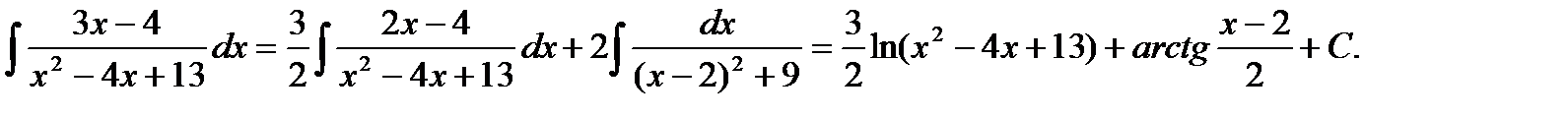
Фундаментом разложения правильной дроби являются следующие теоремы, которые сформулируем без доказательства.
Теорема 1. Любой многочлен n -го порядка можно представить в виде произведения двучленов(x - xi) и неразложимых трехчленов (x 2 + px + q), причем некоторые из них могут быть кратными.
Например 2x6+7x5+8x4+6x3+4x2-x-2=  (2x-1)(x+2)(x+1)2(x2+1). (12)
(2x-1)(x+2)(x+1)2(x2+1). (12)
Теорема 2. Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях.
Так, многочлены P3(x)= ax3+bx2+cx+d, Q3(x)=mx3+kx2+px+q будут равны, если a=m, b=k, c=p, d=q.
Теорема 3. Две рациональные дроби равны, если равны многочлены числителей и соответственно знаменателей дробей.
Т.е. равенство 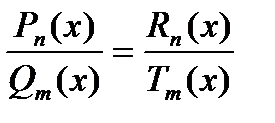 будет соблюдаться, если Pn(x)= Rn(x), Qm(x)= Tm(x).
будет соблюдаться, если Pn(x)= Rn(x), Qm(x)= Tm(x).
Выше, было показано, что неправильную дробь можно представить как сумму многочлена и правильной дроби. Если правильную дробь разложить на сумму простых дробей, которые могут быть проинтегрированы, то и любая рациональная дробь может быть проинтегрирована.
Теорема 4. Правильная рациональная дробь может быть разложена на сумму простых дробей, знаменателями которых будут множители разложения знаменателя правильной дроби.
Пусть дана правильная дробь в виде 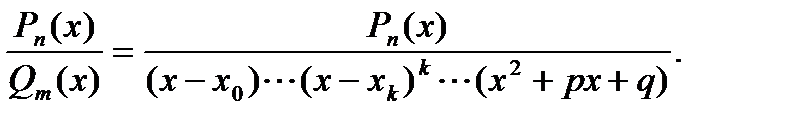
Раскладывая правильную дробь на сумму простых, каждому двучлену в первой степени разложения Qm (x) отвечает простая дробь 1 вида, двучлену степени k – отвечают k дробей 1 и 2 видов с увеличивающимися степенями двучлена (x - xk) от единицы до k, а каждому неразложимому трехчлену – дробь 3 вида. Коэффициенты числителей простых дробей неопределенные и подлежат определению. Для этого простые дроби необходимо привести к общему знаменателю и привести подобные члены. Затем на основании теоремы 3 и 2 приравнять коэффициенты при одинаковых степенях многочлена числителя исходной дроби и числителя дроби с неопределенными коэффициентами. В результате получим систему алгебраических уравнений относительно неопределенных коэффициентов.
Таким образом, после отыскания значений неопределенных коэффициентов и постановки их в простые дроби, интегрирование правильной дроби сведется к интегрированию простых дробей.
Пример.  После представления дроби в виде суммы простых дробей (выше приведенное равенство без знаков интеграла и дифференциала переменной), приведения к общему знаменателю и подобных членов, получим:
После представления дроби в виде суммы простых дробей (выше приведенное равенство без знаков интеграла и дифференциала переменной), приведения к общему знаменателю и подобных членов, получим:
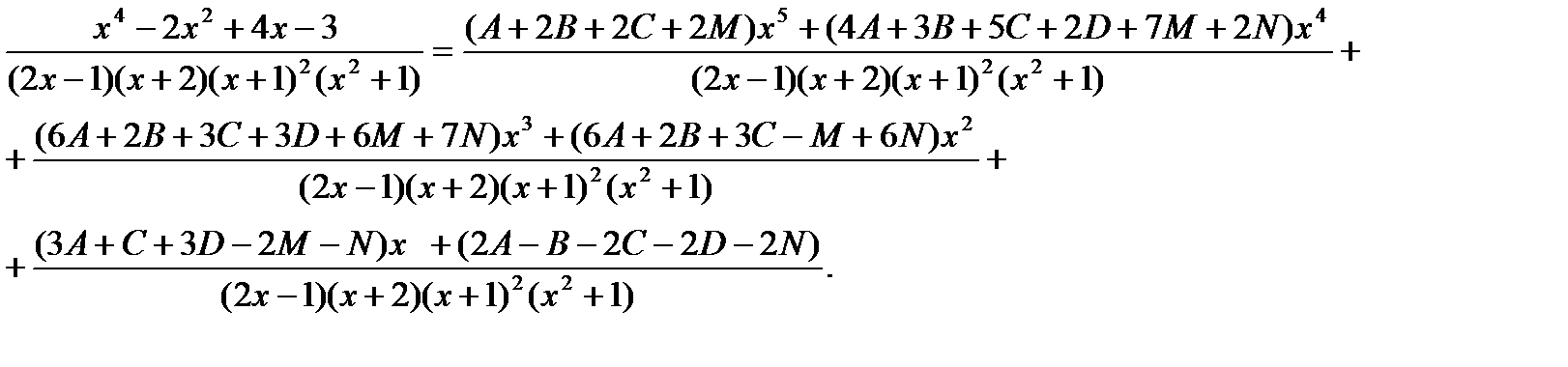
Для того чтобы две дроби были равны необходимо чтобы были равны многочлены в числителях, так как многочлены в знаменателях равны. В силу теоремы 2 приравняем коэффициенты при одинаковых степенях.
В результате получили систему шести алгебраических уравнений относительно коэффициентов. Решая систему, получим следующие значения коэффициентов: 

После подстановки коэффициентов получаем:


Число неизвестных в системе можно уменьшить, используя теорему о равенстве двух функций. Применение этой теоремы значительно облегчает вычисление коэффициентов, когда знаменатель дроби раскладывается на двучлены.
Теорема. Если две функции равны, то равны их значения при одинаковых значениях аргументов функций, т.е., если f (x) = g (x), то f (x 0) = g (x 0).
Рассмотрим пример. Вычислить интеграл 
 Разложим дробь на простые дроби приведем их к общему знаменателю –
Разложим дробь на простые дроби приведем их к общему знаменателю –
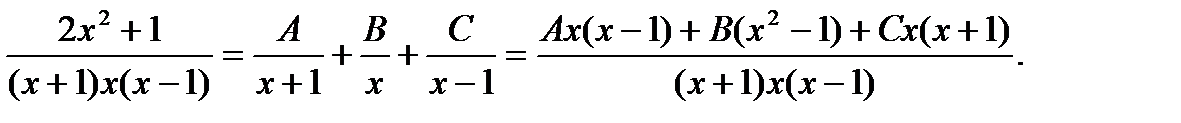
Нетрудно видеть, что значениями аргумента следует выбирать значения переменной обращающие в ноль каждый двучлен. В нашем случае принимая x=-1,x= 0,x= +1 и, подставляя в левый и правый многочлены числителей, получим A= 3/2; B=-1; C=3/2.
Интегрируя простые дроби, вычислим интеграл
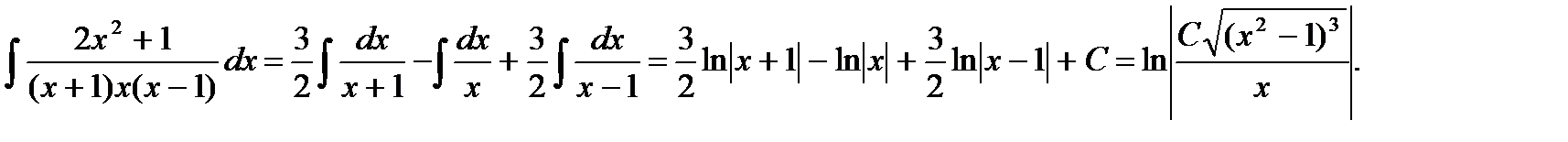
Лекция 4.
§6. Интегрирование некоторых иррациональных функций.
Рассмотрим интегрирование функции, рациональной относительно переменной и различных радикалов из неё, т.е. R(x, 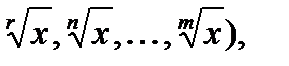 Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например.
Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например. 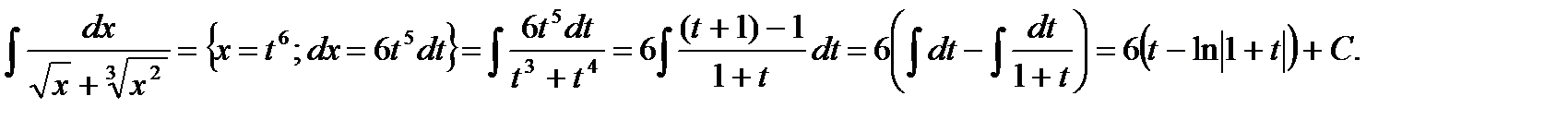
Практически ничего не меняется, если подкоренное выражение есть одна и та же дробно линейная функция 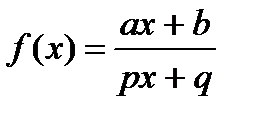 , особенно, если p=0, q =1.
, особенно, если p=0, q =1.
Рассмотрим несколько интегралов, зависящих от иррационального выражения 
1.Если интеграл имеет вид  , то преобразуя радикал к виду
, то преобразуя радикал к виду 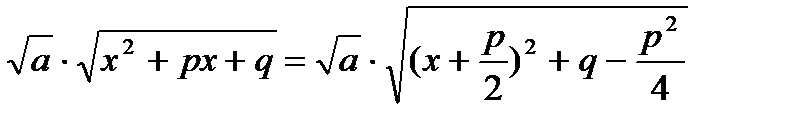 и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например
и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например 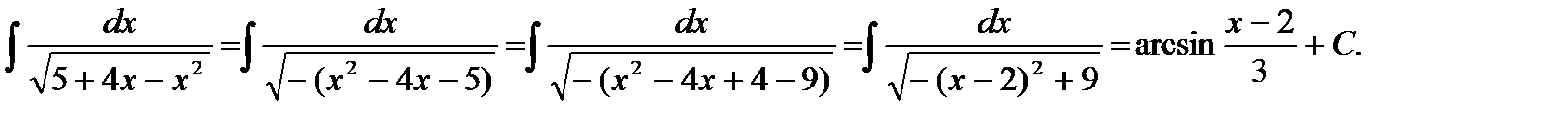
2. Интеграл вида 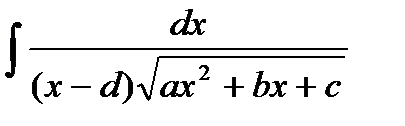 заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
3. Интегралы 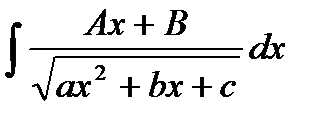 представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
4. Интегралы с функциями вида а) 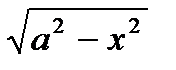 , б)
, б) 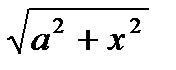 , в)
, в) 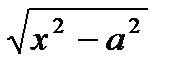 соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
Примеры.1.  =
= 
Нередко функции вида б), в) преобразуют используя замены гиперболическими функциями x = a·sht, x = a·cht, учитывая соотношения ch2t – sh2t = 1; 2ch2t = 1 + ch2t; 2sh2t= ch2t – 1. Так, 2. 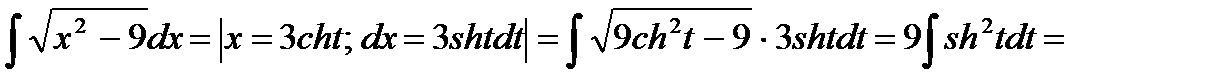
3. 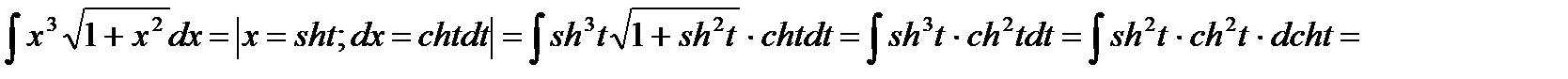 =
= 
Интегралы вида  заменами функций одной переменной сводятся к интегралам от рациональных функций
заменами функций одной переменной сводятся к интегралам от рациональных функций  Например
Например 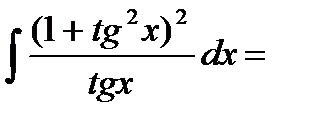

Определенный интеграл.
§7. Задача о вычислении площади криволинейной трапеции.
Определение. Фигура, ограниченная тремя прямыми, две из которых перпендикулярны третьей, и некоторой кривой, называется криволинейной трапецией.
Поставим задачу вычисления площади такой трапеции, ибо ни одна из формул евклидовой геометрии не может быть применена. Для этого введем декартову систему координат так, что ось ординат будет параллельна двум прямым, а ось абсцисс совпадает с третьей. Пусть кривая в заданной системе описывается функцией y= f(x), а трапеция
Для того чтобы представилась возможность применить известные формулы вычисления площади разобьем произвольным образом отрезок [a,b] на n частей (рис.1а). Каждую точку разбиения обозначим так, что x
0 = a, x
n = b. Рассмотрим «i» отрезок (рис1б), называемый элементом разбиения, длина которого ∆x
i = x
i – x
i-1 (i=1,2,3,……,n). Внутри каждого элемента разбиения выберем произвольную точку M
i(φ
i y
i = f(φ
i)) и заменим каждую криволинейную трапецию на отрезках ∆x
i прямоугольниками с высотами f(φ
i). В силу малости отрезков разбиения ∆x
i площадь каждого такого прямоугольника мало отличается по величине от криволинейной трапеции на каждом отрезке. Таким образом, величина площади на каждом элементе будет – ∆S
i = f(φ
i)· ∆x
i. Сумма всех элементарных площадей
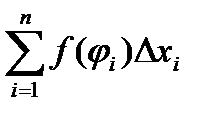
, называемая
интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
S =  (13)
(13)
Итак, площадь криволинейной трапеции равна пределу интегральной суммы при бесконечном увеличении числа разбиений.
§8 Определенный интеграл. Теорема существования.
Рассмотрим последовательность действий составления предела вида (13), отвлекаясь от физического смысла переменных и их обозначений –
1.отрезок [a,b], в котором задана непрерывная функция f(x), разбивается на n частей точками xi (i = 0,1,2,3,……,n), причем x0 = a<x1<x2<…..<xn-1<xn = b;
2.значение функции f(µi) в произвольно выбранной точке µiϵ [xi-1; xi]каждого элемента разбиения умножается на длину элемента ∆xi = xi – xi-1;
3.берется сумма всех таких произведений ln= f(µ1) ∆xi1+ f(µ2) ∆x2+…+ f(µn) ∆xn =
4.находится предел интегральной суммы (14) при стремлении к нулю максимальной длины элемента разбиения и, следовательно, при увеличении числа элементов разбиения, т.е. при n→∞:
I = 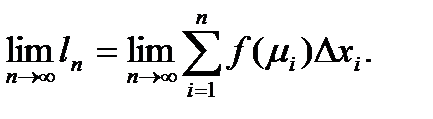 (15)
(15)
Предел (15) принято называть определенным интегралом или интегралом от функции f(x) в пределах от a до b и обозначается:
I = 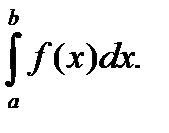 (16)
(16)
Ясно, что
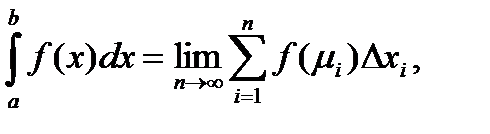
где f(x) называется подынтегральной функцией, f(x)dx - подынтегральным выражением, a,b – пределами интегрирования.
Определение. Определенным интегралом называется предел интегральной суммы (15) при увеличении числа элементов разбиения и стремлении к нулю наибольшего элемента разбиения, если он существует и не зависит от способа разбиения отрезка [ a, b ] выбора точки внутри каждого элемента разбиения.
Вообще говоря, интегральные суммы могут значительно отличаться друг от друга в зависимости от способа разбиения. Однако, для непрерывных функций это различие стирается при увеличении числа разбиений и стремлении максимальной длины элемента разбиения к нулю.
Теорема. Определенный интеграл существует, если подынтегральная функция непрерывна на множестве точек отрезка интегрирования [ a, b ].
Лекция 5.
§9. Свойства определенного интеграла. Теорема о среднем.
Учитывая определение определенного интеграла как предела интегральной суммы, перечислим без доказательства те свойства интеграла, которые доказываются с помощью свойств предела функции:
1.постоянный множитель можно выносить из под знака интеграла –
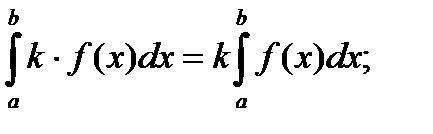
2. интеграл от суммы функций равен сумме интегралов от каждой функции –
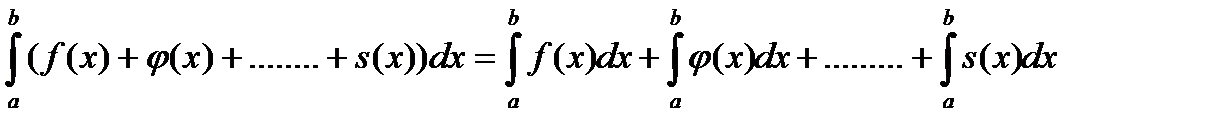
3. если отрезок интегрирования разбит на два участка, то интеграл от функции на отрезке интегрирования равен сумме интегралов от функции на обоих участках, т.е. если [a,b] = [a,c]+[c,b], то  ;
;
4. если f(x) ≥ 0 на отрезке [a,b], то и 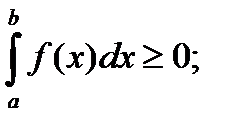
5. если f(x) ≥ φ(x) на [a,b], то и 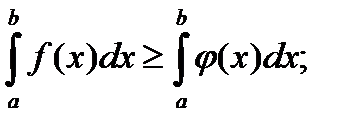
6. если поменять местами пределы интегрирования, то интеграл поменяет знак –
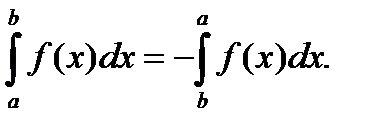
Доказательство этого свойства следует из изменения направления отсчета от b к a, когда xi < xi-1.
Теорема о среднем. Если подынтегральная функция непрерывна [ a, b ], то внутри отрезка найдется такая точка x = c, что выполняется равенство
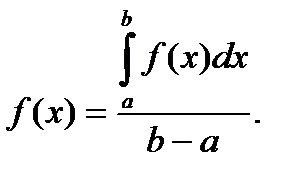 (17)
(17)
Доказательство. Так как функция непрерывна на отрезке, то по свойству функций непрарывных на отрезке она принимает свое нименьшее и наибольшее значение, т.е. она ограничена снизу и сверху. Пусть наименьшее m, а M наибольшее значения функции. Таким образом, выполняется неравенство
m ≤ f(x) ≤ M. (18)
Проинтегрируем неравество и, учитывая свойство 5, получим
m(b-a) ≤  ≤ M(b-a) (19)
≤ M(b-a) (19)
или m ≤  ≤ M.
≤ M.
Из свойств функций непрерывных на отрезки функция принимает все свои промежуточные значения и, следовательно, найдется точка cϵ[a.b], такая, что выполняется равенство (17).
§10. Теорема о производной определенного интеграла по переменному верхнему пределу.
Теорема. Производная от интеграла по переменному верхнему пределу равна подынтегральной функции
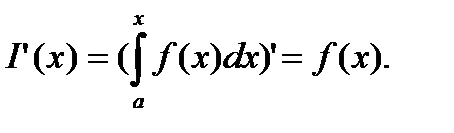 (20)
(20)
Доказательство. Из решения задачи отыскания площади криволинейной трапеции можно сказать, что геометрическим смыслом определенного интеграла является площадь и, следовательно, интеграл можно рассматривать как функции верхнего предела. Дадим приращение ∆x верхнему пределу и найдем приращение функции ∆I = I(x +∆x)-I(x) –
∆I = 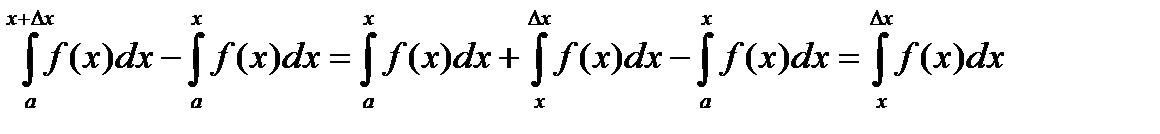 (21)
(21)
В выражении (21) первый интеграл представлен в виде суммы двух в соответствии со свойством 3 §9. Преобразуем последний интеграл, используя теорему о среднем –

где  . Очевидно, что при стремлении приращения аргумента к нулю
. Очевидно, что при стремлении приращения аргумента к нулю 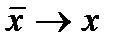 . По определению производной имеем
. По определению производной имеем
I’(x) = 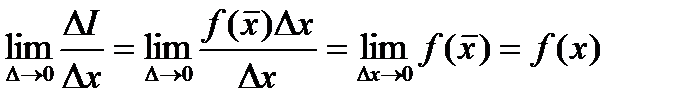
Теорема доказана.
Ее результат позволяет утверждать, что определенный интеграл с переменным верхним пределом есть первообразная подынтегральной функции. А это означает, что вычисление определенного интеграла можно произвести без вычисления предела.
§11. Формула Ньютона-Лейбница.
Теорема. Значение определенного интеграла равно разности значений любой первообразной подынтегральной функции, взятые при верхнем и нижнем пределах интеграла:
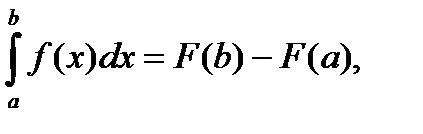 где F’(x) = f(x) (22)
где F’(x) = f(x) (22)
Равенство (22) называется формулой Ньютона – Лейбница.
Доказательство. Рассмотрим функцию
 , которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
, которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
I(a) = F(a) + C =  = 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
= 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
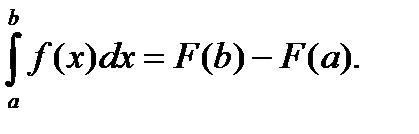
Теорема доказана.
Правую часть формулы Ньютона – Лейбница принято записывать в виде 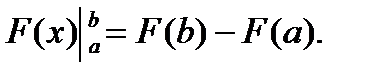
Примеры. Вычислить. 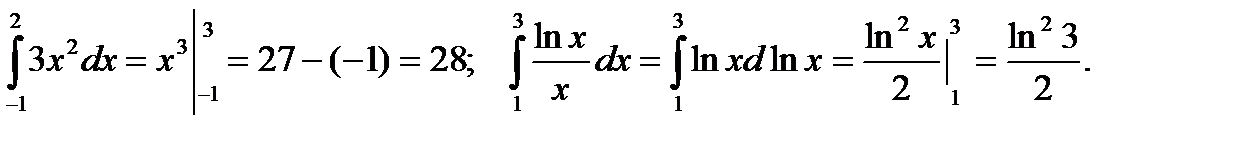
Если подынтегральная функция четная и пределы интегрирования симметричны относительно начала координат, то интеграл удваивается, а нижний предел принимается равным нулю.
Вычислить. 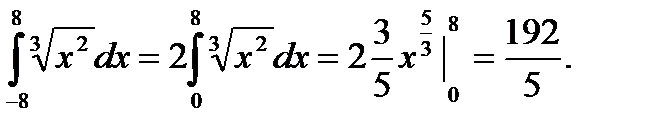
Интегрирование по частям в определенном интеграле производится по той же формуле что и в неопределенном интеграле, но с подстановкой пределов в слагаемые правой части:
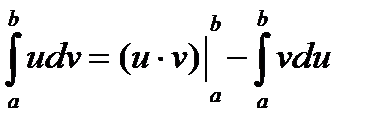 (23)
(23)
Пример.Вычислить. 
Правило замены переменной (подстановки) сводится к следующему: если в интервале [ c, d ] функции x =φ(u), φ’(u), f [φ(u)] непрерывны и φ(c) = a, φ(d) = b, то
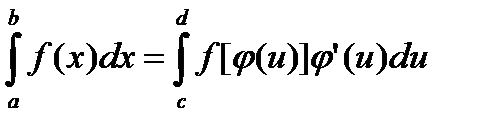 (24)
(24)
Из формулы (24) следует, что, производя замену переменной
x = φ(u), (25)
следует также заменить дифференциал dx, дифференцируя равенство (25) и заменить пределы интегрирования, вновь используя равенство (25) непосредственно или выразив u через x: u= ψ(x). Последнюю операцию лучше производить, используя табличную форму вида:
Пример. 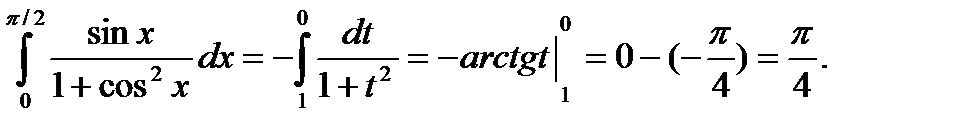
В примере произвели замену cosx = t, dt = -sinxdx


 II.
II.  III.
III. 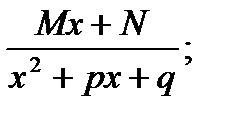 IY.
IY. 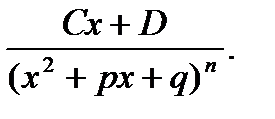 Здесь коэффициенты A,B,C,D,M,N - некоторые константы, a,b,p,q - заданные числа, x2+px+q – неразложимый трехчлен (p2-4q<0).
Здесь коэффициенты A,B,C,D,M,N - некоторые константы, a,b,p,q - заданные числа, x2+px+q – неразложимый трехчлен (p2-4q<0). Представляем интеграл суммой интегралов. В первом - арифметическими операциями в числителе добиваемся выражения производной. Для
Представляем интеграл суммой интегралов. В первом - арифметическими операциями в числителе добиваемся выражения производной. Для

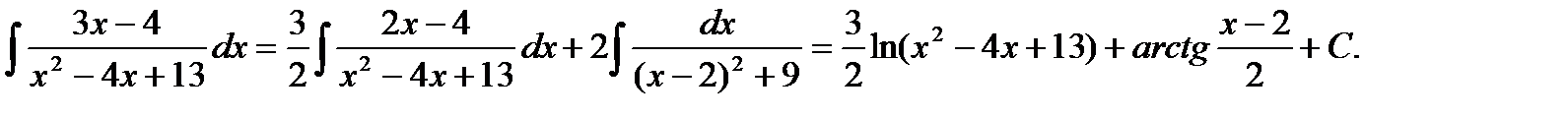
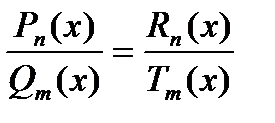 будет соблюдаться, если Pn(x)= Rn(x), Qm(x)= Tm(x).
будет соблюдаться, если Pn(x)= Rn(x), Qm(x)= Tm(x).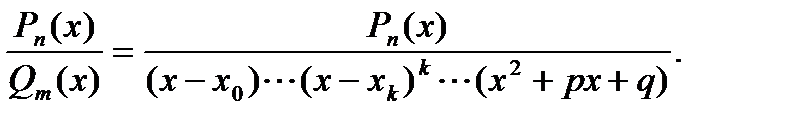
 После представления дроби в виде суммы простых дробей (выше приведенное равенство без знаков интеграла и дифференциала переменной), приведения к общему знаменателю и подобных членов, получим:
После представления дроби в виде суммы простых дробей (выше приведенное равенство без знаков интеграла и дифференциала переменной), приведения к общему знаменателю и подобных членов, получим: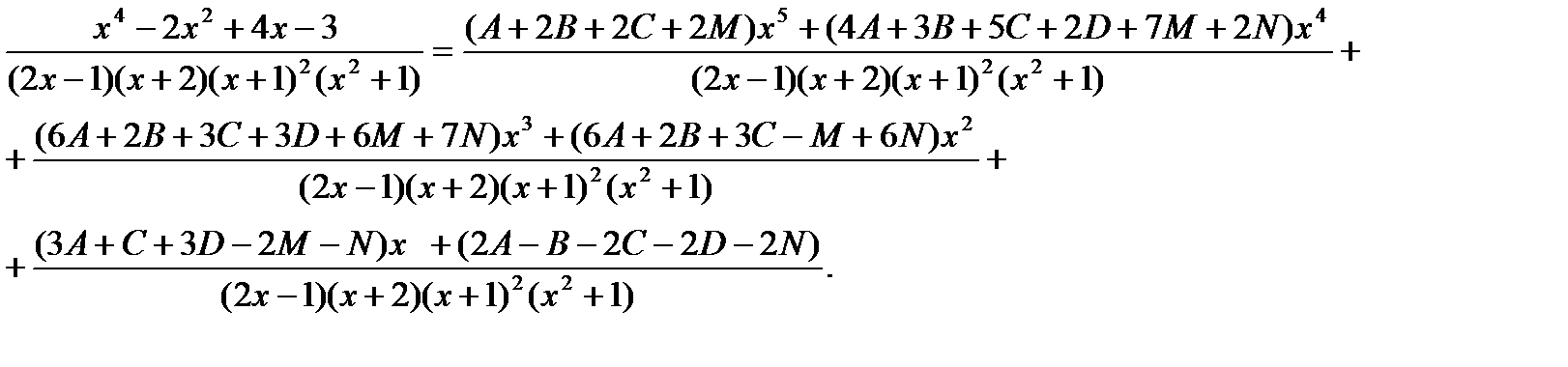





 Разложим дробь на простые дроби приведем их к общему знаменателю –
Разложим дробь на простые дроби приведем их к общему знаменателю –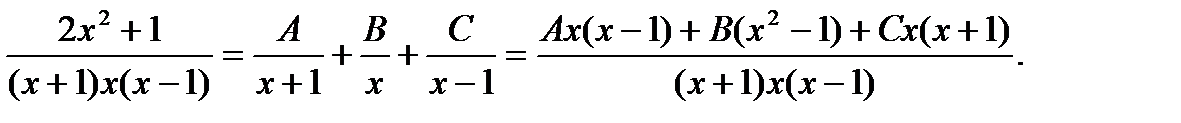
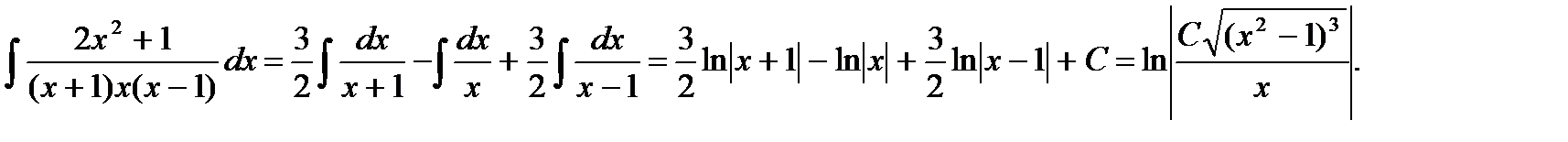
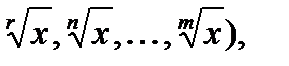 Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например.
Интегрирование сводится к интегрированию рациональной функции относительно новой переменой после замены x=tr, где r – наименьшее общее кратное показателей радикалов. Например. 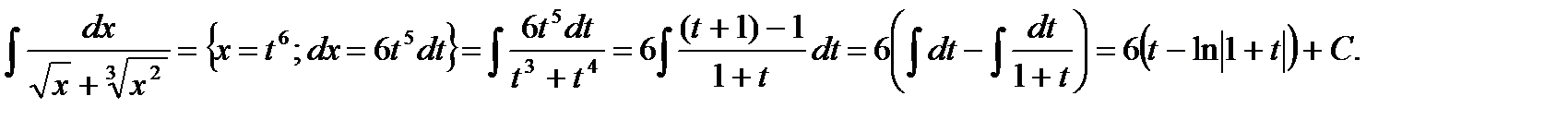
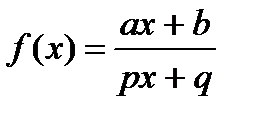 , особенно, если p=0, q =1.
, особенно, если p=0, q =1.
 , то преобразуя радикал к виду
, то преобразуя радикал к виду 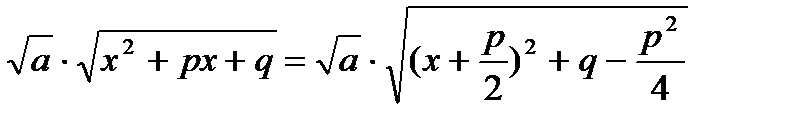 и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например
и выделяя полный квадрат, приводим интеграл к табличному(a – может быть отрицательным). Например 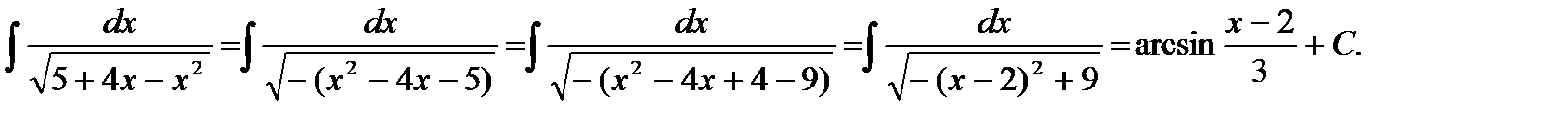
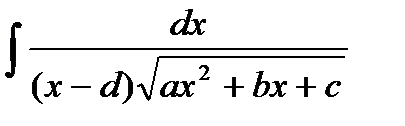 заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.
заменой x-d = 1/t; dx = -dt/t2 сводится к рассмотренному в п.1.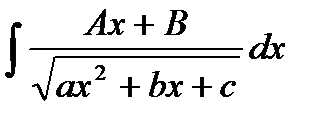 представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).
представляют суммой двух интегралов, которые преобразуются подобно простой дроби вида 3 (§5 п. Разложение на простые дроби).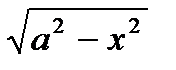 , б)
, б) 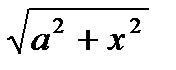 , в)
, в) 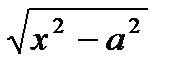 соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций.
соответствующими заменами x=aSint, x=atgt, x=a/Sint сводятся к интегрированию тригонометрических функций. =
= 
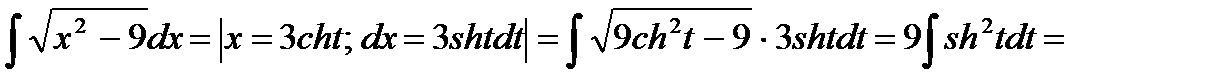
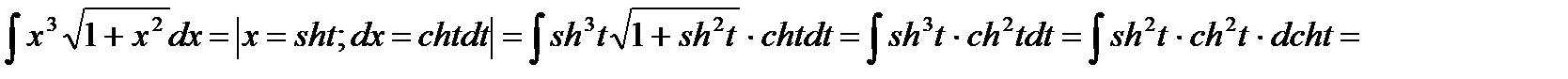 =
= 
 заменами функций одной переменной сводятся к интегралам от рациональных функций
заменами функций одной переменной сводятся к интегралам от рациональных функций  Например
Например 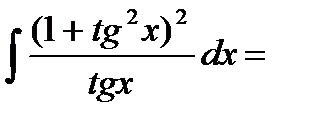

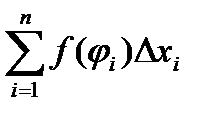 , называемая интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
, называемая интегральной, приблизительно равна площади всей криволинейной трапеции и она будет точнее с увеличением числа разбиений. Следовательно,
 (13)
(13)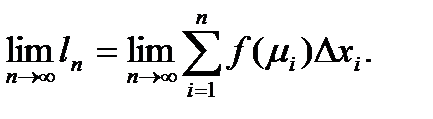 (15)
(15)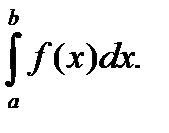 (16)
(16)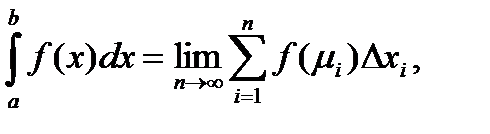
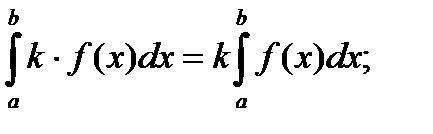
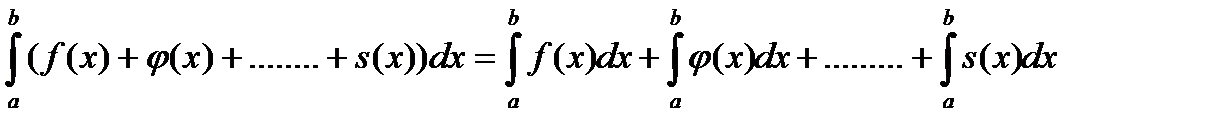
 ;
;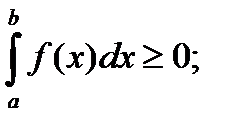
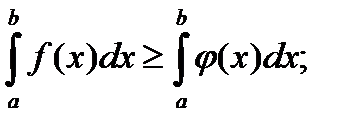
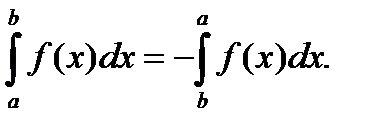
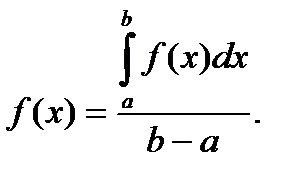 (17)
(17) ≤ M(b-a) (19)
≤ M(b-a) (19)  ≤ M.
≤ M. 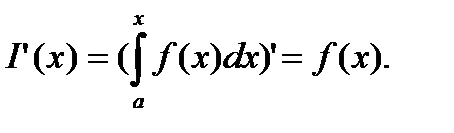 (20)
(20)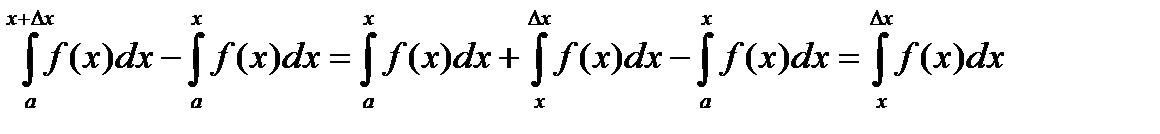 (21)
(21)
 . Очевидно, что при стремлении приращения аргумента к нулю
. Очевидно, что при стремлении приращения аргумента к нулю  . По определению производной имеем
. По определению производной имеем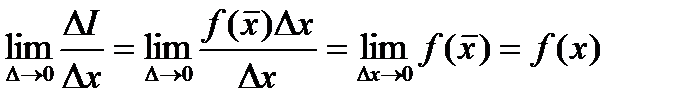
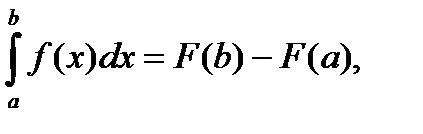 где F’(x) = f(x) (22)
где F’(x) = f(x) (22) , которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a.
, которая, как было показано выше в §10, является перообразной подынтегральной функции. Вычислим значение функции при x =a. = 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим:
= 0, следовательно, C =-F(a). Теперь, подставляя x=b и учитывая C = -F(a), получим: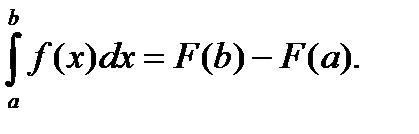
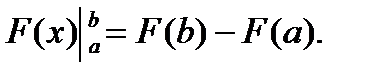
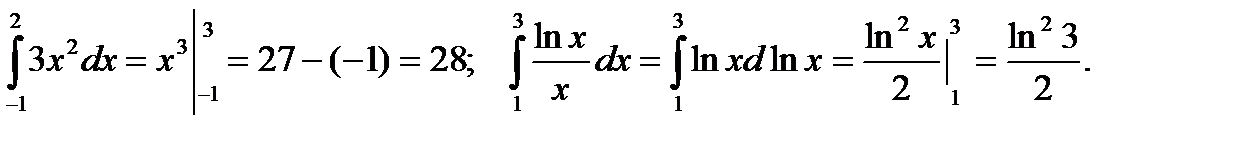
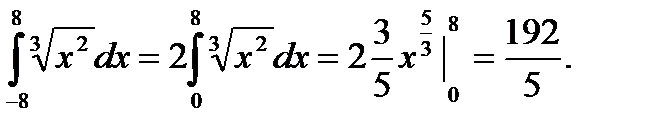
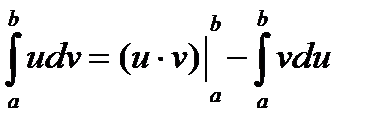 (23)
(23)
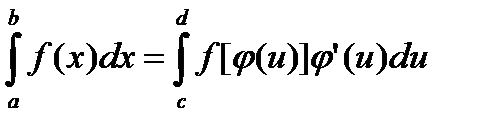 (24)
(24)