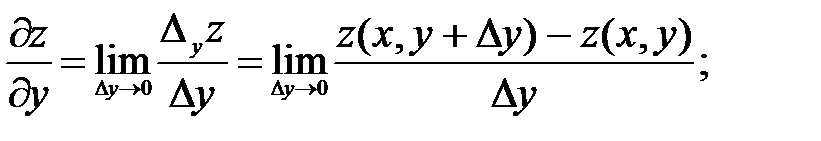§16 Функции многих переменных
В первом семестре мы изучали функции одной переменной. Но наряду с величинами, зависящими от одной переменной, существуют величины, меняющимися от двух, трех и многих величин. Так, например, площадь прямоугольника зависит от размеров двух его сторон: S = x·y, объём параллелепипеда зависит от трех независимых величин – его сторон: V = x·y·z, работа электрического тока на участке цепи зависит от разности потенциалов U на концах участках, силы тока I и времени t: A = I·U·t, и т.д.
Пусть задано некоторое множество D двух переменных x, y. Геометрически множество D может совпадать со всей плоскостью, либо некоторой частью ее – открытой или замкнутой. Значения переменных x, y определяют в этой области точку P(x; y) в системе координат. Дадим определение функции двух переменных.
Определение Величина z называется функцией переменных x и y на множестве D, если каждой точке этого множества ставится в соответствие определенное значение z.
В общем случае такую функцию принято обозначать: z = z(x;y), u=f(v;w), s = w(t;v). Обе части этих равенств равноправны. Левая часть – краткое обозначение функции. В правой - в скобках указываются символы переменных, а перед скобкой – символ, который указывает на существование закона, соответствия двум значениям независимых переменных x, y определенного значения функции. Частные значения функции и аргументов обозначаются индексированием соответствующих символов – z0 = z(x0;y0). Так, если z = 2x2 – 3y3, то z(-2;-1) = 2·(-2)2 - 3·(-1)3 = 8 + 3 = 11.
Заметим, что в пространственном базисе совокупности трех значений отвечает точка в пространстве. Следовательно, геометрическим образом функции двух переменных является некоторая поверхность. Подтверждением этого служит плоскость, общим уравнением которой является функция z = Ax + By + D.
Перечислим способы задания функции двух переменных: табличный, графический и аналитический.
Задавая функцию в виде таблицы, ее значение находят на пересечении столбца и строки, в начале которых задаются значения аргументов. Недостатки: трудность определения промежуточных значений, отсутствие наглядность поведения функции. Достоинство – быстрота определения значения функции.
Графиком функции в заданной системе координа т называется множество точек, (аппликата). Достоинство – наглядность поведения функции.
Аналитический способ заключается в задании функции в виде формулы. Этот способ позволяет производить необходимые математические преобразования, т.е. дает возможность применять к этой функции аппарат математического анализа.
Определение. Величина u называется функцией переменных x, y, z,….., t, если каждой совокупности этих переменных соответствует одно определенной значение величины u.
Обозначается функция так – u = f(x,y,z,…..,t). Вместо символа f может стоять любая буква. Если функцию u нельзя выразить через аргументы, то записывают в виде F(x,y,z,…..,t,u) = 0. Эту запись называют заданием функции в неявном виде.
§17 Предел и непрерывность функции
Определения предела и непрерывности можно свести к определению предела и непрерывности функции одной переменной. Для простоты изложения рассмотрим функцию двух переменных z = z(x;y). В декартовой системе координат совокупности значений x, y на плоскости отвечает точка P(x;y). Следовательно, функцию z = z(x;y) можно рассматривать как функцию одной переменной – переменной точки P, т.е. z = z(P). При перемещении точки P значения x, y будут меняться, а вместе с ними будут меняться значения функции. j
Пусть задана некоторая точка P0(x0;y0).
Определение. Назовем ρ – окрестностью точки P 0 множество точек P, удовлетворяющих неравенству | 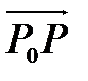 | < ρ. (31)
| < ρ. (31)
В координатной системе векторному неравенству (31) отвечает скалярное неравенство:
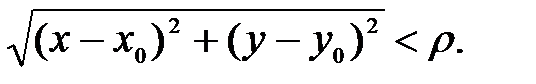 (32)
(32)
Неравенству (32) геометрически соответствует круг радиуса ρ (рис.4). Очевидно, что если P(x;y) стремится к P(x0;y0), то аргументы x. y стремятся к x0, y0 соответственно. Таким образом, если 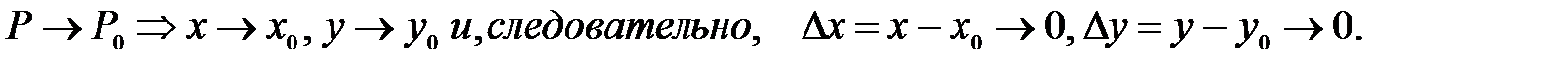
Определение. Число A называется пределом функции z (P) при P стремящимся к P 0, если для любого ε > 0 найдется такая ρ-окрестность точки P 0, что при выполнении неравенства | P 0 P |<ρ будет выполняться неравенство | z - A |<ε.
Другими словами. чем ближе точка P к точке P0, тем меньше разность значений функции z(x;y) и предела A, но значение функции в точке P0 может и не существовать.
Пусть значение функции z = z(x;y) в точке P0 – z0 = z(x0;y0). Дадим аргументам этой точки приращения ∆x, ∆y и получим точку P1(x+∆x;y+∆y), значение функции в которой z1 = z(x+∆x;y+∆y)
Определение. Приращением функции z = z (x; y) в точке P 0 называется разность значений функций в точках P 1 и P 0, т.е.
∆ z = z (x 0 +∆ x; y 0 +∆ y) - z (x 0; y 0). (33)
Если точка произвольная, то приращение функции ∆z = z(x+∆x;y+∆y) - z(x;y).
Определение. Функция называется непрерывной в точке, если она определена в этой точке и некоторой окрестности ее и бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, т.е.
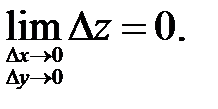 (34)
(34)
Если в равенстве (33) обозначить x = x 0 +∆ x, y = y 0 +∆ y, условие непрерывности можно переписать в виде -
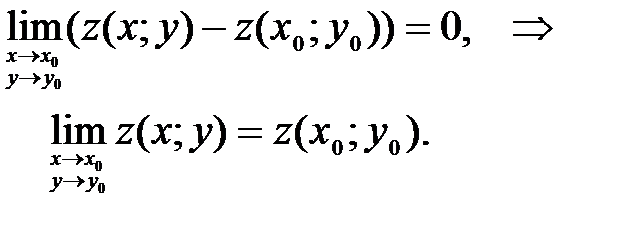
Последнее равенство означает, что если функция z = z(x;y) непрерывна в точке P0, то ее значение в этой точке равно z(x0;y0).
Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
Точки, в которых не выполняются условия непрерывности, называются точками разрыва.
Например, функция 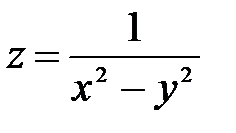 непрерывна во всех точках плоскости x, y кроме точек прямых y = x и y = -x. На этих прямых функция не определена, значения функции не существуют.
непрерывна во всех точках плоскости x, y кроме точек прямых y = x и y = -x. На этих прямых функция не определена, значения функции не существуют.
§18 Частные производные функции многих переменных
Определение. Частным приращением функции многих производных называется приращение, вызванное приращением только одного аргумента при фиксированных остальных.
Пусть задана функция двух переменных z = z(x;y) и пусть аргумент x получил приращение ∆x. Тогда приращение функции z(x+∆x;y) - z(x;y) называется частным по переменной x и обозначается ∆xz = z(x+∆x;y) - z(x;y). В соответствии с определением приращение ∆yz = z(x;y + ∆y) - z(x;y) является частным по переменной y.
Определение. Частной производной функции многих переменных называется предел отношения частного приращения к приращению аргумента, вызвавшего приращение функции, когда приращение аргумента стремится к нулю.
Применительно к функции двух переменных частные производные, которые принято обозначать  , будут
, будут
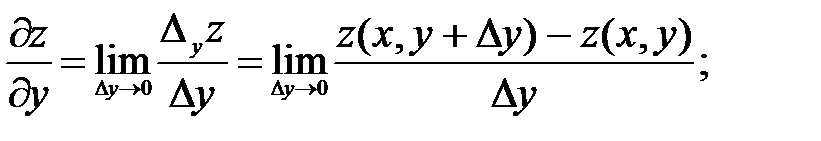

Из определения частной производной следует простое правило дифференцирования, учитывая, что при вычислении производной, и только, функция становится функцией одной переменной, остальные считаются постоянными. Поэтому все способы вычисления производной функции одной переменной автоматически переносятся на вычисление частной производной по выбранной переменной, обращаясь с остальными как с константами.
Примеры. Найти частные производные функции 1) z = x2y3 + Sin(xy2).
zx’ = 2xy3 + y2Cos(xy2); zy’ = 3x2y2 + 2xyCos(xy2).
2) w = uvlnv wu’ = vlnv; wv’ = u(lnv + v(1/v)) = u(lnv + 1). 3) u = st При дифференцировании по s функция u считается степенной, а по t - показательной и поэтому us’ = t·st-1, ut’ = stlns.
Геометрически частная производная численно равна тангенсу угла наклона касательной к кривой, полученной пересечением поверхности z = z (x; y) и плоскостью, уравнением которой является фиксированная переменная.



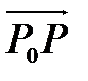 | < ρ. (31)
| < ρ. (31) 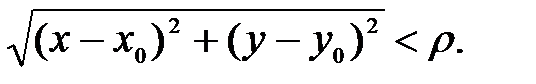 (32)
(32)
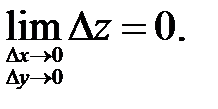 (34)
(34)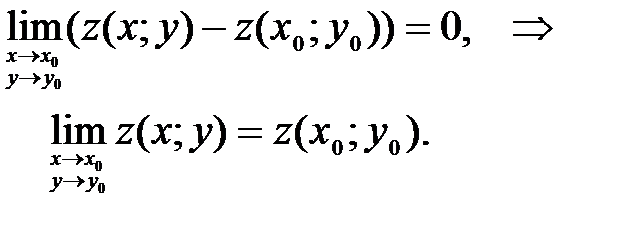
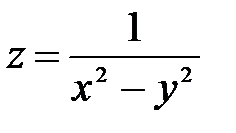 непрерывна во всех точках плоскости x, y кроме точек прямых y = x и y = -x. На этих прямых функция не определена, значения функции не существуют.
непрерывна во всех точках плоскости x, y кроме точек прямых y = x и y = -x. На этих прямых функция не определена, значения функции не существуют. , будут
, будут