321. Алгебраические многочлены. Теорема Безу.
Многочленом или полиномом n - й степени  будем называть сумму
будем называть сумму  , где коэффициенты
, где коэффициенты  , есть комплексные числа и переменная z принимает значения из множества
, есть комплексные числа и переменная z принимает значения из множества  . В частности, как
. В частности, как  , так и z могут быть действительными. Коэффициент
, так и z могут быть действительными. Коэффициент  называется свободным членом.
называется свободным членом.
Таким образом,
 . (1)
. (1)
Число  называется нулем или корнем многочлена
называется нулем или корнем многочлена  ,
,
если  .
.
Разделить многочлен  на двучлен
на двучлен  , где а есть заданное число, значит представить его в виде
, где а есть заданное число, значит представить его в виде
 , (2)
, (2)
где  есть многочлен степени
есть многочлен степени  , а r называют остатком
, а r называют остатком
от деления многочлена на  . При этом допускают, что равенство (2) выполняетcя для всех значений
. При этом допускают, что равенство (2) выполняетcя для всех значений  (или
(или  ). Если
). Если  , то
, то
говорят, что многочлен делится на  .
.
Коэффициенты многочлена  и остаток r можно высчитывать согласно рекуррентным формулам
и остаток r можно высчитывать согласно рекуррентным формулам
 .
.
При вычислениях используют таблицу
Верхняя строка этой таблицы задана, а нижняя постепенно заполняется согласно с заданными выше формулами. Такой способ нахождения некоторого частного и остатка при делении многочлена на двучлен называют схемой Горнера.
Теорема 1 (Безу). Число  является корнем многочлена
является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  делится без остатка на
делится без остатка на  , т.е. если
, т.е. если
 , (4)
, (4)
где  – многочлен степени
– многочлен степени  .
.
Доказательство. Необходимость. Пусть  – корень многочлена
– корень многочлена  , т. е.
, т. е.  . Согласно равенству (2) при
. Согласно равенству (2) при  имеем
имеем  . Таким образом,
. Таким образом,  , что означает делимость многочлена
, что означает делимость многочлена  на
на  .
.
Достаточность. Если многочлен делится на  , то это означает справедливость равенства (4), откуда следует, что
, то это означает справедливость равенства (4), откуда следует, что  . Таким образом,
. Таким образом,  есть корень многочлена
есть корень многочлена  . □
. □
Ответ на вопрос о существовании корня многочлена дает следующая теорема.
Теорема 2 (основная теорема алгебры). Всякий многочлен положительной степени имеет хотя бы один корень (действительный или комплексный).
322. Разложение многочлена на множители.
10. Число  называется корнем многочлена
называется корнем многочлена  кратности k, если
кратности k, если  можно представить в виде
можно представить в виде

 . (1)
. (1)
Другими словами, если  делится без остатка на
делится без остатка на 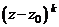 и не делится на
и не делится на  , то k называется кратностью корня
, то k называется кратностью корня  .
.
Если, в свою очередь, число  является корнем многочлена
является корнем многочлена  кратности
кратности  , то
, то  , где
, где  . Продолжая этот процесс, через конечное число шагов m получим многочлен нулевой степени
. Продолжая этот процесс, через конечное число шагов m получим многочлен нулевой степени  , причем
, причем  .
.
Таким образом, если  – корни многочлена
– корни многочлена  кратности
кратности  , соответственно, причем
, соответственно, причем  , то имеет место следующее разложение многочлена
, то имеет место следующее разложение многочлена  на множители
на множители
 , (2)
, (2)
т.е. всякий многочлен n -й степени раскладывается на n линейных множителей типа  и числовой множитель, равный коэффициенту при
и числовой множитель, равный коэффициенту при  .
.
Пусть  есть действительный корень кратности k многочлена
есть действительный корень кратности k многочлена  с действительными коэффициентами. Тогда этот многочлен можно записать в виде (1).
с действительными коэффициентами. Тогда этот многочлен можно записать в виде (1).
Пусть теперь  , есть комплексный корень многочлена
, есть комплексный корень многочлена  , тогда и число
, тогда и число  также будет корнем этого многочлена. Действительно, используя свойства комплексно-сопряженных чисел, получим
также будет корнем этого многочлена. Действительно, используя свойства комплексно-сопряженных чисел, получим


 .
.
Отсюда, если  , то
, то  , т. е.
, т. е.  – корень многочлена
– корень многочлена  .
.
Следовательно, в разложении многочлена  на множители будет присутствовать произведение
на множители будет присутствовать произведение  .
.
Отсюда следует, если  – корень кратности k, то и
– корень кратности k, то и  − корень кратности k. Другими словами, многочлен
− корень кратности k. Другими словами, многочлен  в этом случае можно представить в виде
в этом случае можно представить в виде

 . (3)
. (3)
Имеем
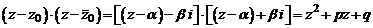 ,
,
где  ,
,  – действительные числа.
– действительные числа.
Легко видеть, что трехчлен  имеет дискриминант
имеет дискриминант  .
.
Таким образом, если  – комплексный корень трехчлена
– комплексный корень трехчлена  , то дискриминант
, то дискриминант  . Справедливо и обратное: если
. Справедливо и обратное: если  , то трехчлен имеет комплексно-сопряженные корни:
, то трехчлен имеет комплексно-сопряженные корни:
 .
.
Из вышеизложенного вытекает: если  и
и  − комплексно-сопряженные корни многочлена
− комплексно-сопряженные корни многочлена  кратности k, то, в силу представления (3), имеет место разложение
кратности k, то, в силу представления (3), имеет место разложение
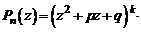
 , (3/)
, (3/)
где  – действительные числа,
– действительные числа, 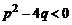 , а для многочлена
, а для многочлена  с действительными коэффициентами числа
с действительными коэффициентами числа  ,
,  не являются его корнями, т.е.
не являются его корнями, т.е.  ,
,  .
.
Пусть  – все действительные корни многочлена
– все действительные корни многочлена  , а их кратности соответственно равны
, а их кратности соответственно равны  , где
, где  . Тогда многочлен
. Тогда многочлен  , согласно формуле (1), можно представить в виде
, согласно формуле (1), можно представить в виде  , где
, где  – многочлен степени
– многочлен степени  с действительными коэффициентами,
с действительными коэффициентами,
который не имеет действительных корней.
Если  – многочлен ненулевой степени, то каждой паре комплексно-сопряженных корней
– многочлен ненулевой степени, то каждой паре комплексно-сопряженных корней  кратности
кратности  соответствует множитель
соответствует множитель  из формулы (3/), где
из формулы (3/), где  .
.
С учетом этого обстоятельства получим
 (4)
(4)
где 
 .
.
Таким образом, зная все корни многочлена  с действительными коэффициентами, можно его разложить на множители с действительными коэффициентами, это значит представить в виде (4), где числа
с действительными коэффициентами, можно его разложить на множители с действительными коэффициентами, это значит представить в виде (4), где числа  – действительные.
– действительные.
20. Тождественность двух многочленов. Выясним условие, при котором два многочлена тождественны. Перейдем здесь от обозначения переменной z к x, подчеркивая тем самым, что все дальнейшие рассмотрения будут проводиться в области действительных чисел.
Утверждение 1. Многочлен  равен нулю тогда и только тогда, когда все его коэффициенты равны нулю.
равен нулю тогда и только тогда, когда все его коэффициенты равны нулю.
Доказательство. Действительно, согласно формуле (2), многочлен 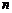 -ой степени
-ой степени  можно представить в виде
можно представить в виде
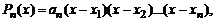 (2΄)
(2΄)
где  – корни этого многочлена, среди которых могут быть и равные.
– корни этого многочлена, среди которых могут быть и равные.
Из разложения (2΄) следует, что многочлен 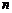 -ой степени не может иметь более чем
-ой степени не может иметь более чем 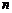 корней с учетом их кратности. Если же он обращается в нуль при
корней с учетом их кратности. Если же он обращается в нуль при  различных значениях
различных значениях  то этот многочлен тождественно равен нулю. В самом деле, т.к.
то этот многочлен тождественно равен нулю. В самом деле, т.к.  но ни один из его линейных множителей в (2΄) не равен нулю, следует, что
но ни один из его линейных множителей в (2΄) не равен нулю, следует, что  , а значит, согласно той же формуле (2),
, а значит, согласно той же формуле (2),  тождественно равен нулю.
тождественно равен нулю.
Обратно, если многочлен тождественно равен нулю, то он равен нулю и при некотором значении 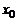 переменной
переменной 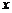 , которое не совпадает с
, которое не совпадает с  . В таком случае ни один из множителей
. В таком случае ни один из множителей  не равен нулю, а поэтому
не равен нулю, а поэтому  Повторяя рассуждения для многочлена
Повторяя рассуждения для многочлена  уже с высшим коэффициентом
уже с высшим коэффициентом  аналогично показываем, что
аналогично показываем, что 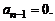 Таким же образом доказывается
Таким же образом доказывается  ☐
☐
Утверждение 2. Два многочлена  и
и 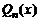 тождественно равны друг другу тогда и только тогда, когда у них совпадают коэффициенты при одинаковых степенях
тождественно равны друг другу тогда и только тогда, когда у них совпадают коэффициенты при одинаковых степенях 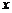 .
.
Доказательство. Это утверждение следует из того, что разность данных многочленов есть многочлен, тождественно равный нулю. Тогда, на основании утверждения 1, все его коэффициенты равны нулю. ☐
30. Признак кратности корня.
Утверждение 3. Если 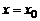 – корень кратности k многочлена
– корень кратности k многочлена  , то
, то 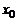 является корнем кратности
является корнем кратности 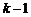 его производной
его производной 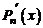 .
.
Доказательство. Действительно, если 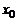 − корень кратности k многочлена
− корень кратности k многочлена  , то имеет место представление
, то имеет место представление
 . (5)
. (5)
Дифференцируя это равенство, получаем
 ,
,
где  , т.е.
, т.е. 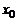 является корнем кратности
является корнем кратности 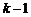 производной
производной 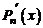 . □
. □
Следствие 1. Для того, чтобы число 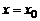 было корнем кратности
было корнем кратности  , многочлена
, многочлена  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы

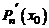

 . (6)
. (6)
Множество действительных чисел. Модуль действительного числа. Ограниченные и неограниченные числовые множества. Наибольший и наименьший элементы числового множества. Верхняя и нижняя грани числового множества.
331. Множество действительных чисел.
Целые положительные числа 1,2,3… называются натуральными. Множество натуральных чисел обозначают N.
Рациональные числа – все целые, нуль и дробные числа.
Каждое рациональное число можно представить в виде  , где p – целое число, q – натуральное число.
, где p – целое число, q – натуральное число.
Рациональное число можно представить также в виде периодической десятичной дроби. Иррациональные числа – бесконечная непериодическая дробь.
Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают R.
Каждое действительное число изображается точкой числовой оси и, обратно, каждой точке числовой оси соответствует единственное действительное число.
1. Интервалом называется множество действительных чисел х, удовлетворяющих неравенству a < x < b, где a, b – действительные числа. Обозначается (a,b).
2. Отрезком (сегментом) называется множество действительных чисел, удовлетворяющих неравенству a ≤ x ≤ b. Обозначается [ a, b ].
3. Интервал длины 2ε, с центром в точке х0 называют окрестностью точки х0х0 – ε < х < х0 + ε.
4. Интервалы могут быть бесконечные: (а, + ∞), (- ∞, а), (-∞, +∞), [ a, + ∞),
(- ∞, a ].
332. Модуль действительного числа. Ограниченные и неограниченные числовые множества.


 будем называть сумму
будем называть сумму  , где коэффициенты
, где коэффициенты  , есть комплексные числа и переменная z принимает значения из множества
, есть комплексные числа и переменная z принимает значения из множества  . В частности, как
. В частности, как  называется свободным членом.
называется свободным членом. . (1)
. (1) называется нулем или корнем многочлена
называется нулем или корнем многочлена  .
. , где а есть заданное число, значит представить его в виде
, где а есть заданное число, значит представить его в виде , (2)
, (2) есть многочлен степени
есть многочлен степени  , а r называют остатком
, а r называют остатком  (или
(или  ). Если
). Если  , то
, то  и остаток r можно высчитывать согласно рекуррентным формулам
и остаток r можно высчитывать согласно рекуррентным формулам .
.




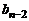

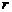
 делится без остатка на
делится без остатка на  , т.е. если
, т.е. если , (4)
, (4) – многочлен степени
– многочлен степени  имеем
имеем  . Таким образом,
. Таким образом,  на
на 
 . (1)
. (1)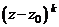 и не делится на
и не делится на  , то k называется кратностью корня
, то k называется кратностью корня  является корнем многочлена
является корнем многочлена  кратности
кратности  , то
, то  , где
, где  . Продолжая этот процесс, через конечное число шагов m получим многочлен нулевой степени
. Продолжая этот процесс, через конечное число шагов m получим многочлен нулевой степени  , причем
, причем  .
. – корни многочлена
– корни многочлена  , соответственно, причем
, соответственно, причем  , то имеет место следующее разложение многочлена
, то имеет место следующее разложение многочлена  , (2)
, (2) .
. , есть комплексный корень многочлена
, есть комплексный корень многочлена  также будет корнем этого многочлена. Действительно, используя свойства комплексно-сопряженных чисел, получим
также будет корнем этого многочлена. Действительно, используя свойства комплексно-сопряженных чисел, получим

 .
. , т. е.
, т. е.  – корень многочлена
– корень многочлена  .
.
 . (3)
. (3)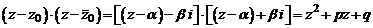 ,
, ,
,  – действительные числа.
– действительные числа. имеет дискриминант
имеет дискриминант  .
. . Справедливо и обратное: если
. Справедливо и обратное: если  .
.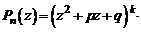
 – действительные числа,
– действительные числа, 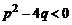 , а для многочлена
, а для многочлена  ,
,  .
. – все действительные корни многочлена
– все действительные корни многочлена  , где
, где  . Тогда многочлен
. Тогда многочлен  , где
, где  – многочлен степени
– многочлен степени  с действительными коэффициентами,
с действительными коэффициентами, кратности
кратности  соответствует множитель
соответствует множитель  из формулы (3/), где
из формулы (3/), где  .
.  (4)
(4)
 .
. – действительные.
– действительные. равен нулю тогда и только тогда, когда все его коэффициенты равны нулю.
равен нулю тогда и только тогда, когда все его коэффициенты равны нулю. -ой степени
-ой степени 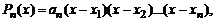 (2΄)
(2΄) – корни этого многочлена, среди которых могут быть и равные.
– корни этого многочлена, среди которых могут быть и равные. различных значениях
различных значениях  то этот многочлен тождественно равен нулю. В самом деле, т.к.
то этот многочлен тождественно равен нулю. В самом деле, т.к.  но ни один из его линейных множителей в (2΄) не равен нулю, следует, что
но ни один из его линейных множителей в (2΄) не равен нулю, следует, что  , а значит, согласно той же формуле (2),
, а значит, согласно той же формуле (2), 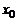 переменной
переменной 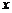 , которое не совпадает с
, которое не совпадает с  не равен нулю, а поэтому
не равен нулю, а поэтому  Повторяя рассуждения для многочлена
Повторяя рассуждения для многочлена  уже с высшим коэффициентом
уже с высшим коэффициентом  аналогично показываем, что
аналогично показываем, что 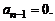 Таким же образом доказывается
Таким же образом доказывается  ☐
☐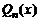 тождественно равны друг другу тогда и только тогда, когда у них совпадают коэффициенты при одинаковых степенях
тождественно равны друг другу тогда и только тогда, когда у них совпадают коэффициенты при одинаковых степенях 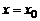 – корень кратности k многочлена
– корень кратности k многочлена  , то
, то 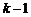 его производной
его производной 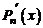 .
. . (5)
. (5) ,
, , т.е.
, т.е.  , многочлена
, многочлена 
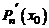

 . (6)
. (6) , где p – целое число, q – натуральное число.
, где p – целое число, q – натуральное число.


