

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение. Говорят, что функция f (x) имеет в точке x 0 максимум (или минимум), если эту точку можно окружить такой окрестностью (x 0 – δ, x 0 + δ), содержащейся в промежутке [ a, b ], где задана функция, что для всех ее точек x выполняется неравенство f (x) < f (x 0) (или f (x) > f (x 0)).
Иными словами, точка x 0доставляет функции f (x) максимум (минимум), если значение f (x 0) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x 0.
Если функция имеет максимумы в точках x 0и x 1, то, применяя к промежутку [ x 0, x 1]2-ю теорему Вейерштрасса (гл.1, §12, п.12.9) видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x 2между x 0и x 1 и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В случае, когда функция имеет конечное число максимумов и минимумов, они попросту чередуются.
Максимумы и минимумы функции называются экстремумами или экстремальными значениями функции.
Укажем метод нахождения экстремальных значений.
Теорема 1(необходимое условие существования экстремума). Если дифференцируемая функция f (x) имеет в точке x = x 0 максимум или минимум, то ее производная в этой точке обращается в нуль, т.е.  = 0.
= 0.
Доказательство этой теоремы достигается применением к промежутку (x 0 – δ, x 0+ δ), о котором была речь выше, теоремы Ферма (§4, п.4.2).
Из теоремы 1 непосредственно вытекает следствие: если при всех рассматриваемых значениях аргумента x функция f (x) имеет производную, то она может иметь экстремум (максимум или минимум) только при тех значениях, при которых производная обращается в нуль (касательная параллельна оси Oх, рис.18, точки x = ξ 1 и x = ξ 2 и рис.25, точки x = x 1и x = x 2). Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует максимум или минимум. Так, на рис.25 изображена функция, у которой при x = x 3 производная обращается в нуль (касательная горизонтальна), но в этой точке функция не имеет, ни максимума, ни минимума, а налицо перегиб, так как касательная пересекает кривую.
|
|
Точки, в которых производная существует и равна нулю, называются стационарными.
Если расширить класс рассматриваемых функций f (x) и допустить, что в отдельных точках производная равна бесконечности или вовсе не существует, то не исключена возможность того, что экстремум придется на какую-либо из таких точек. Например, функция, изображенная на рис.25, очевидно, имеет максимум при x = x 5, в то время как производная ее в этой точке равна ∞; точно также в точке x = 0 имеет максимум функция у = –| x |, хотя производной для нее в этой точке не существует. Следовательно, и точки, в которых производная бесконечна или не существует, также могут доставлять функции экстремум. Но, разумеется, и в этом случае также – одно лишь отсутствие производной или обращение ее в бесконечность не гарантирует наличия экстремума. Примерами могут служить функции 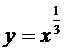 и
и 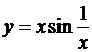 (с дополнительным условием y = 0 при x = 0). Первая из них имеет бесконечную производную в точке x = 0 (см. также рис.16,б, кривые (1) и (2)), вторая же вовсе не имеет производной в этой точке, но точка x = 0 не доставляет экстремума ни той, ни другой функции (ибо в любой ее окрестности обе функции принимают и положительные и отрицательные значения).
(с дополнительным условием y = 0 при x = 0). Первая из них имеет бесконечную производную в точке x = 0 (см. также рис.16,б, кривые (1) и (2)), вторая же вовсе не имеет производной в этой точке, но точка x = 0 не доставляет экстремума ни той, ни другой функции (ибо в любой ее окрестности обе функции принимают и положительные и отрицательные значения).
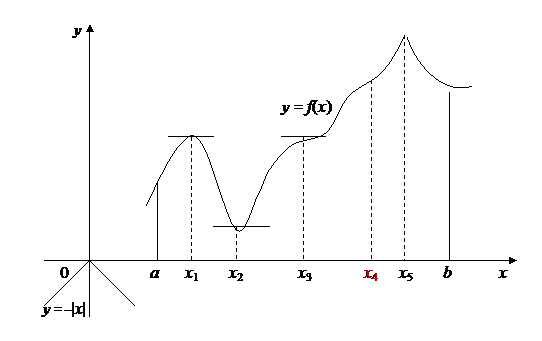
Рис. 25
Таким образом, функция может иметь экстремум лишь в трех случаях: либо в тех точках, где производная существует и равна нулю, либо бесконечности; либо в тех точках, где производной не существует.
Значения аргумента, при которых производная обращается либо в нуль, либо в бесконечность, либо вовсе не существует, называются критическими точками или критическими значениями.
|
|
Из предыдущего следует, что не при всяком критическом значении функция имеет максимум или минимум. Однако, если в какой – либо точке функция достигает максимума или минимума, то эта точка наверняка является критической. Поэтому для разыскания экстремума функции поступают следующим образом: находят все критические точки, а затем, исследуя отдельно каждую критическую точку, выясняют, будет ли в этой точке максимум или минимум функции или же не будет ни максимума, ни минимума.
Исследование функции в критических точках опирается не следующие теоремы.
Теорема 2(достаточные условия существования экстремума). Пусть функция f (x) непрерывна в некоторой окрестности (x 0 – δ, x 0+ δ), точки x 0. Если во всех точках этого интервала (по крайней мере, для x = x 0) существует конечная производная  и как слева от x 0, так и справа от x 0 (в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
и как слева от x 0, так и справа от x 0 (в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
I.  > 0 при x < x 0 и
> 0 при x < x 0 и  < 0 при x > x 0, т.е. производная
< 0 при x > x 0, т.е. производная  при переходе через точку x 0 меняет знак плюс на минус. В этом случае, в промежутке (x 0 – δ, x 0), функция f (x) возрастает, а в промежутке (x 0, x 0+ δ), убывает, так что значение f (x 0) будет наибольшим в промежутке (x 0 – δ, x 0+ δ), т.е. в точке x 0 функция имеет максимум (рис.25, x 0 = x 1).
при переходе через точку x 0 меняет знак плюс на минус. В этом случае, в промежутке (x 0 – δ, x 0), функция f (x) возрастает, а в промежутке (x 0, x 0+ δ), убывает, так что значение f (x 0) будет наибольшим в промежутке (x 0 – δ, x 0+ δ), т.е. в точке x 0 функция имеет максимум (рис.25, x 0 = x 1).
II.  < 0 при x < x 0 и
< 0 при x < x 0 и  > 0 при x > x 0, т.е. производная
> 0 при x > x 0, т.е. производная  при переходе через точку x 0 меняет знак минус на плюс. В этом случае аналогично убеждаемся, что в точке x 0 функция имеет минимум (рис.25, x 0 = x 2).
при переходе через точку x 0 меняет знак минус на плюс. В этом случае аналогично убеждаемся, что в точке x 0 функция имеет минимум (рис.25, x 0 = x 2).
III.  > 0 как при x < x 0, так и при x > x 0, либо же
> 0 как при x < x 0, так и при x > x 0, либо же  < 0 и слева и справа от x 0, т.е. при переходе через x 0,
< 0 и слева и справа от x 0, т.е. при переходе через x 0,  не меняет знака. Тогда функция либо все время возрастает, либо все время убывает; в любой близости от x 0 с одной стороны найдутся точки x, в которых f (x) < f (x 0), а с другой – точки x, в которых f (x) > f (x 0), так что в точке x 0никакого экстремума нет (например, рис.25, x 0 = x 3 – точка перегиба).
не меняет знака. Тогда функция либо все время возрастает, либо все время убывает; в любой близости от x 0 с одной стороны найдутся точки x, в которых f (x) < f (x 0), а с другой – точки x, в которых f (x) > f (x 0), так что в точке x 0никакого экстремума нет (например, рис.25, x 0 = x 3 – точка перегиба).
Итак, мы получаем первое правило для исследования критической точки на экстремум: подставляя в производную  сначала x < x 0, а затем x > x 0, устанавливаем знак производной поблизости от точки x 0 слева и справа от нее; если при этом производная
сначала x < x 0, а затем x > x 0, устанавливаем знак производной поблизости от точки x 0 слева и справа от нее; если при этом производная  меняет знак плюс на минус, то налицо максимум, если меняет знак минус на плюс, то – минимум; если же знака не меняет, то экстремума вовсе нет.
меняет знак плюс на минус, то налицо максимум, если меняет знак минус на плюс, то – минимум; если же знака не меняет, то экстремума вовсе нет.
|
|
В тех случаях, когда критическая точка x 0– стационарная, т.е. 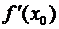 = 0 и в некоторой окрестности точки x 0существует непрерывная вторая производная
= 0 и в некоторой окрестности точки x 0существует непрерывная вторая производная 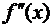 тогда при разыскании экстремумов исследование знака первой производной вблизи испытуемой точки можно заменить исследованием знака второй производной в самой этой точке; покажем это.
тогда при разыскании экстремумов исследование знака первой производной вблизи испытуемой точки можно заменить исследованием знака второй производной в самой этой точке; покажем это.
Итак, пусть функция f (x) не только имеет производную  в окрестности точки x 0, но и вторую производную непрерывную в некоторой окрестности точки x 0. Точка x 0 – стационарная, т.е.
в окрестности точки x 0, но и вторую производную непрерывную в некоторой окрестности точки x 0. Точка x 0 – стационарная, т.е. 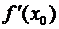 = 0. Если
= 0. Если 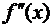 > 0, то, по теореме о сохранении знака непрерывной функции (гл.1, §12, п.12.9, теорема 1) и условия монотонности функции (гл.3, §4, п.4.2.2, теорема 2) – функция
> 0, то, по теореме о сохранении знака непрерывной функции (гл.1, §12, п.12.9, теорема 1) и условия монотонности функции (гл.3, §4, п.4.2.2, теорема 2) – функция  в окрестности точки x = x 0возрастает, т.е. вблизи точки x 0 слева
в окрестности точки x = x 0возрастает, т.е. вблизи точки x 0 слева  <
< 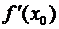 = 0, а справа
= 0, а справа  >
> 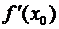 = 0. Таким образом, производная
= 0. Таким образом, производная  меняет знак минус на плюс и, следовательно, f (x) имеет в точке x = x 0минимум. Если
меняет знак минус на плюс и, следовательно, f (x) имеет в точке x = x 0минимум. Если 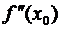 < 0, то
< 0, то  в точке x = x 0убывает, меняя знак плюс на минус, так, что налицо максимум.
в точке x = x 0убывает, меняя знак плюс на минус, так, что налицо максимум.
Таким образом, можно сформулировать второе правило для исследования стационарной точки x 0 на экстремум: подставляем x 0 во вторую производную 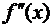 ; если
; если 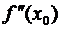 > 0, то функция имеет минимум, если же
> 0, то функция имеет минимум, если же 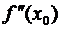 < 0, то – максимум.
< 0, то – максимум.
Второе правило ничего не дает, когда вторая производная в точке x 0 обращается в нуль. В этом случае решение вопроса зависит от поведения высших производных. Если 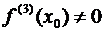 , то из теоремы 1, гл.1, §12, п.12.9 и теоремы 3, гл.3, §7, п.7.1 следует, что точка x 0 есть точка перегиба. Если же
, то из теоремы 1, гл.1, §12, п.12.9 и теоремы 3, гл.3, §7, п.7.1 следует, что точка x 0 есть точка перегиба. Если же 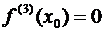 , а
, а 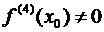 , то в точке x = x 0имеет место экстремум: при
, то в точке x = x 0имеет место экстремум: при 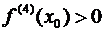 – минимум, а при
– минимум, а при 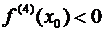 – максимум.
– максимум.
Для большей общности предположим теперь, что не только 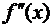 , но и все производные до (n – 1) – го порядка включительно от функции f (x) обращаются в нуль при x = x 0:
, но и все производные до (n – 1) – го порядка включительно от функции f (x) обращаются в нуль при x = x 0: 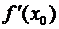 =
= 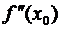 =... =
=... = 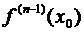 = 0,
= 0,
между тем как 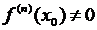 .
.
Тогда справедливо следующее третье правило: если первая из производных, не обращающихся в точке x 0 в нуль, есть производная нечетного порядка (n = 2 m – 1, m 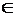 N), функция не имеет в точке x 0 ни максимума, ни минимума (при m ³ 2, в точке x = x 0имеет место перегиб). Если такой производной является производная четного порядка (n = 2 m, m
N), функция не имеет в точке x 0 ни максимума, ни минимума (при m ³ 2, в точке x = x 0имеет место перегиб). Если такой производной является производная четного порядка (n = 2 m, m 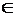 N), функция в точке x 0 имеет максимум или минимум, смотря по тому, будет ли эта производная отрицательна или положительна.
N), функция в точке x 0 имеет максимум или минимум, смотря по тому, будет ли эта производная отрицательна или положительна.
|
|
Поставим теперь вопрос о разыскании наибольшего и наименьшего из всех значений, которые непрерывная функция f (x) принимает на промежутке [ a, b ]; по 2-ой теореме Вейерштрасса (гл.1, §12, п.12.9), такие наибольшие и наименьшие значения существуют.
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!