Если мы имеем неопределенности следующих видов: 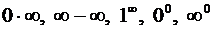 , то все они путем алгебраических преобразований приводятся к виду
, то все они путем алгебраических преобразований приводятся к виду 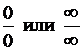 , для которых можно воспользоваться правилом Лопиталя. Пусть
, для которых можно воспользоваться правилом Лопиталя. Пусть
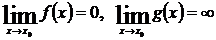 .
.
Тогда имеем:
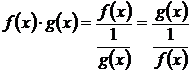 .
.
Второе из этих выражений представляет при х ® х 0 неопределенность вида 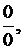 третье – неопределенность вида
третье – неопределенность вида 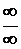 .
.
Пример 1. 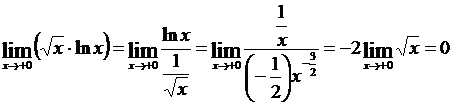 .
.
Если 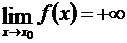 и
и 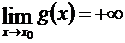 ,
,  то выражение
то выражение 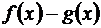 можно привести, например, к неопределенности вида
можно привести, например, к неопределенности вида 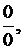 путем следующих преобразований:
путем следующих преобразований:
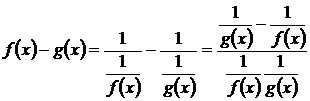 .
.
Часто, впрочем, найти предел этого выражения удается проще.
Пример 2.
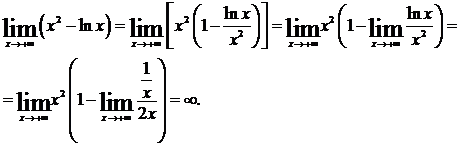
В случае неопределенных выражений вида 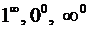 рекомендуется предварительно прологарифмировать.
рекомендуется предварительно прологарифмировать.
Пусть 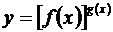 и в окрестности точки х 0
и в окрестности точки х 0 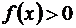 , тогда
, тогда
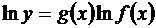 .
.
Предел  представляет собой неопределенность уже изученного типа 0·¥ (или ¥·0). Допустим, что одним из указанных выше приемов удается найти
представляет собой неопределенность уже изученного типа 0·¥ (или ¥·0). Допустим, что одним из указанных выше приемов удается найти
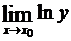 , который оказывается равным конечному числу т, +¥ или –¥. Тогда
, который оказывается равным конечному числу т, +¥ или –¥. Тогда 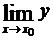 , соответственно, будет ет,+¥ или 0.
, соответственно, будет ет,+¥ или 0.
Пример 3. Вычислить 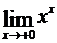 . Положив у = хх, находим:
. Положив у = хх, находим:

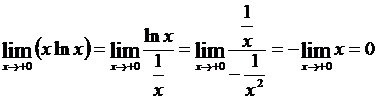 .
.
 Следовательно,
Следовательно, 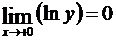 , откуда
, откуда 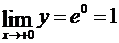 , т.е.
, т.е. 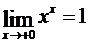 .
.
Пример 4.
Пусть 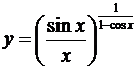 . Требуется найти
. Требуется найти 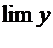 при
при 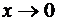 (неопределенность вида
(неопределенность вида 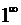 ).
).
Если считать х > 0 (этим предположением, ввиду четности функции у, можно ограничиться), то
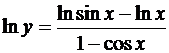 .
.
Пользуясь последовательно дважды правилом Лопиталя, получим:
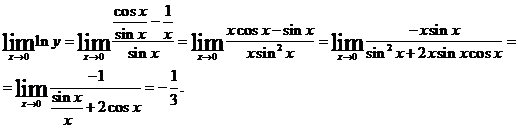
Откуда 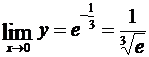 .
.
Заметим, что не все неопределенности можно раскрыть с помощью правила Лопиталя. Например,
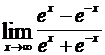 .
.
Однако этот предел можно найти другим способом. Действительно, разделив заданную дробь на ех, получим:

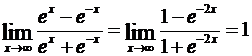 .
.

Формула Тейлора
Устанавливаемая в этом параграфе формула является одной из основных формул математического анализа и имеет многочисленные приложения, как в анализе, так и в смежных дисциплинах. Данная формула устанавливает способ приближенного отображения, или, как говорят, способы аппроксимации произвольной функции с помощью полиномов (многочленов), которые являются наиболее простыми среди всех других функций.
Предположим, что функция 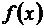 имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х 0. Найдем многочлен Рп (х) степени не выше п, значение которого в точке х 0 равняется значению функции
имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х 0. Найдем многочлен Рп (х) степени не выше п, значение которого в точке х 0 равняется значению функции 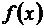 в этой точке, а значения его производных до п- го порядка в точке х = х 0 равняются значениям соответствующих производных от функции
в этой точке, а значения его производных до п- го порядка в точке х = х 0 равняются значениям соответствующих производных от функции 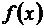 в этой точке.
в этой точке.
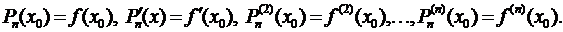 (3.43)
(3.43)
Естественно ожидать, что такой многочлен в некотором смысле «близок» к функции 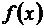 .
.
Будем искать этот многочлен в форме многочлена по степеням (х – х 0) с неопределенными коэффициентами
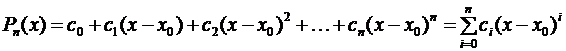 (3.44)
(3.44)
Неопределенные коэффициенты ci, i = 0, 1, 2, …, п определим так, чтобы удовлетворялись условия (3.43).
Предварительно найдем производные от Рп (х):
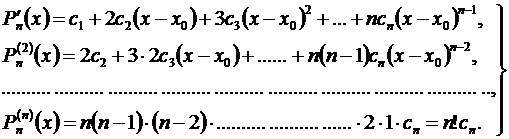 (3.45)
(3.45)
Подставляя в левые и правые части равенств (3.44) и (3.45) вместо х значение х 0и заменяя на основании равенств (3.43) Рп (х 0) через 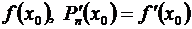 и т.д., получим:
и т.д., получим:
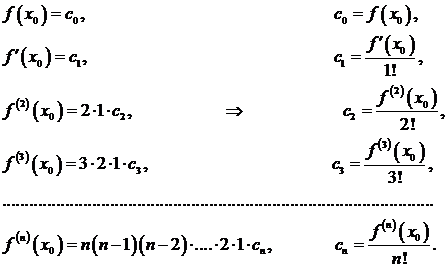
Подставляя найденные значения сi в формулу (3.44), получим искомый многочлен: 
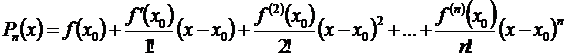 . (3.46)
. (3.46)
Многочлен (3.46) называют многочленом Тейлора для функции 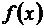 . Обозначим через Rn +1(х) разность значений данной функции
. Обозначим через Rn +1(х) разность значений данной функции 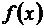 и построенного многочлена Pn (x): Rn +1(х) =
и построенного многочлена Pn (x): Rn +1(х) = 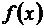 – Pn (x).
– Pn (x).
Откуда 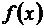 = Pn (x) + Rn +1(х), или, в развернутом виде:
= Pn (x) + Rn +1(х), или, в развернутом виде:
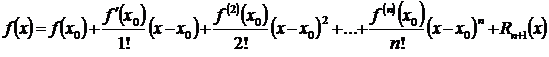 . (3.47)
. (3.47)
Выражение (3.47) называют формулой Тейлора для функции 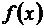 в окрестности точки х 0, а Rn+ 1(х) – остаточным (дополнительным) членом формулы Тейлора. Для тех значений х, для которых остаточный член Rn +1(х) мал, многочлен Pn (x) дает приближенное значение функции
в окрестности точки х 0, а Rn+ 1(х) – остаточным (дополнительным) членом формулы Тейлора. Для тех значений х, для которых остаточный член Rn +1(х) мал, многочлен Pn (x) дает приближенное значение функции 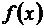 .
.
Таким образом, формула (3.47) дает возможность заменить функцию
у = 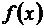 многочленом у = Pn (x) с соответствующей степенью точности, равной значению остаточного члена Rn +1(х). Можно показать, что такое представление функции
многочленом у = Pn (x) с соответствующей степенью точности, равной значению остаточного члена Rn +1(х). Можно показать, что такое представление функции 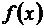 единственно, т.е., что, если имеем одновременно, вблизи х 0,
единственно, т.е., что, если имеем одновременно, вблизи х 0,
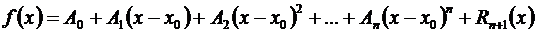 ,
,
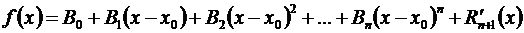 ,
,
то необходимо А 0 = В 0, А 1 = В 1,…, Ап = Вп.
Для остаточного члена получено довольно много различных форм представления, одно из которых имеет вид:
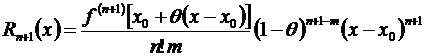 , (3.48)
, (3.48)
где т – произвольное положительное число, 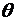 – число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.
– число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.
Из него, придавая т конкретные значения, можно получить более частные формы остаточного члена. Положив т = п + 1, получим остаточный член в форме Лагранжа:
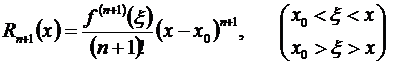 . (3.49)
. (3.49)
Он напоминает следующий очередной член формулы Тейлора, лишь вместо того, чтобы вычислять (п + 1)-ю производную в точке х 0, эту производную берут для некоторого среднего (между х 0 и х) значения 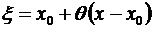 .
.
При т = 1 приходим к остаточному члену в форме Коши.
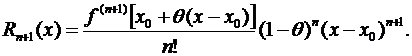 (3.50)
(3.50)
Так как формы Лагранжа и Коши отвечают разным значениям m, а θ зависит от m, то значения θ в формулах (3.49) и (3.50) является, вообще говоря, различными. Обе формы остаточного члена (Лагранжа и Коши) обычно используются в тех случаях, когда требуется при тех или иных фиксированных значениях х, отличных от х 0, приближенно вычислить функцию 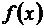 с наперед указанной степенью точности, которую можно оценить по формулам (3.49) и (3.50) для данного х, а также воздействовать на нее за счет изменения n. Наряду с этим встречаются задачи в которых нас интересует не численная величина указанной ошибки, а лишь порядок ее относительно малой величины (х – х 0). Для этой цели удобна форма записи остаточного члена в виде
с наперед указанной степенью точности, которую можно оценить по формулам (3.49) и (3.50) для данного х, а также воздействовать на нее за счет изменения n. Наряду с этим встречаются задачи в которых нас интересует не численная величина указанной ошибки, а лишь порядок ее относительно малой величины (х – х 0). Для этой цели удобна форма записи остаточного члена в виде
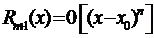 . (3.51).
. (3.51).
Данная формула означает, что при стремлении х к х 0 остаточный член 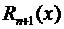 представляет собой бесконечно малую порядка выше n -го по сравнению с (х – х 0), т.е.
представляет собой бесконечно малую порядка выше n -го по сравнению с (х – х 0), т.е. 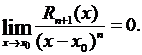 Равенство (3.51) называют остаточным членом, представленным в форме Пеано.
Равенство (3.51) называют остаточным членом, представленным в форме Пеано.
Формулу Тейлора (3.47) часто записывают в несколько ином виде. Положив в (3.47) (х – х 0) = Δ х, х = х 0 + Δ х и f (х) – f (х 0) = Δ f (х 0) получаем
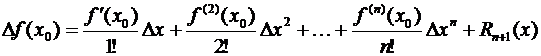 (3.52)
(3.52)
с точностью до дополнительного члена, таким образом, приращение функции разложено по степеням приращения независимой переменной.
Далее, вспоминая, что
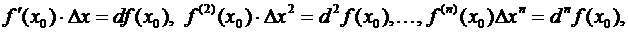
мы можем переписать (3.52) в такой форме
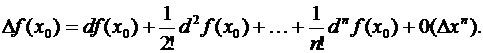
Здесь остаточный член записан в форме Пеано. Отсюда видим, что при 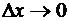 последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно
последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно 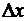 ) в разложении бесконечно малого приращения функции.
) в разложении бесконечно малого приращения функции.
Если в (3.52) остаточный член записать в форме Лагранжа (3.49), то формула Тейлора (3.52) с остаточным членом в форме Лагранжа (3.49) является естественным обобщением формулы Лагранжа (3.34). Формула Лагранжа (3.34) конечных приращений получается из формулы (3.52) в частном случае n = 0.



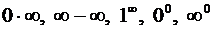 , то все они путем алгебраических преобразований приводятся к виду
, то все они путем алгебраических преобразований приводятся к виду 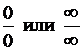 , для которых можно воспользоваться правилом Лопиталя. Пусть
, для которых можно воспользоваться правилом Лопиталя. Пусть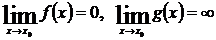 .
.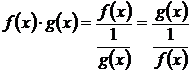 .
.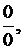 третье – неопределенность вида
третье – неопределенность вида 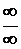 .
.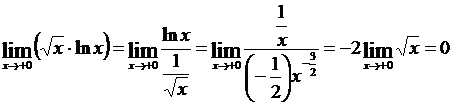 .
.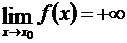 и
и 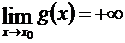 ,
,  то выражение
то выражение 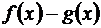 можно привести, например, к неопределенности вида
можно привести, например, к неопределенности вида 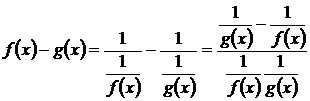 .
.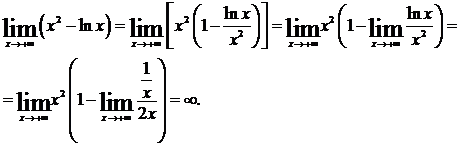
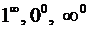 рекомендуется предварительно прологарифмировать.
рекомендуется предварительно прологарифмировать.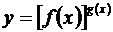 и в окрестности точки х 0
и в окрестности точки х 0 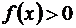 , тогда
, тогда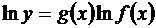 .
. представляет собой неопределенность уже изученного типа 0·¥ (или ¥·0). Допустим, что одним из указанных выше приемов удается найти
представляет собой неопределенность уже изученного типа 0·¥ (или ¥·0). Допустим, что одним из указанных выше приемов удается найти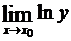 , который оказывается равным конечному числу т, +¥ или –¥. Тогда
, который оказывается равным конечному числу т, +¥ или –¥. Тогда 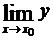 , соответственно, будет ет,+¥ или 0.
, соответственно, будет ет,+¥ или 0.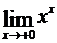 . Положив у = хх, находим:
. Положив у = хх, находим: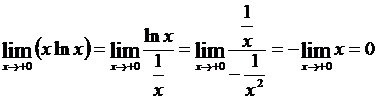 .
.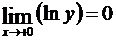 , откуда
, откуда 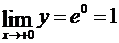 , т.е.
, т.е. 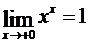 .
.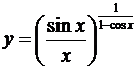 . Требуется найти
. Требуется найти 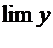 при
при 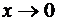 (неопределенность вида
(неопределенность вида 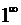 ).
).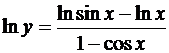 .
.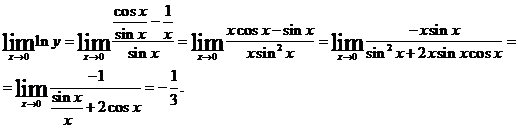
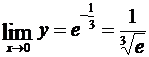 .
.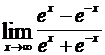 .
.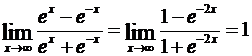 .
.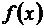 имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х 0. Найдем многочлен Рп (х) степени не выше п, значение которого в точке х 0 равняется значению функции
имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х 0. Найдем многочлен Рп (х) степени не выше п, значение которого в точке х 0 равняется значению функции 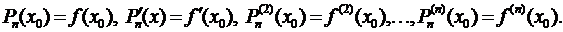 (3.43)
(3.43)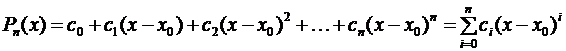 (3.44)
(3.44)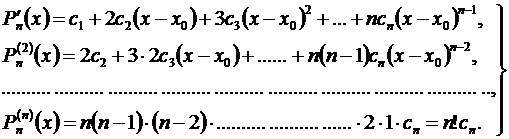 (3.45)
(3.45)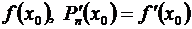 и т.д., получим:
и т.д., получим: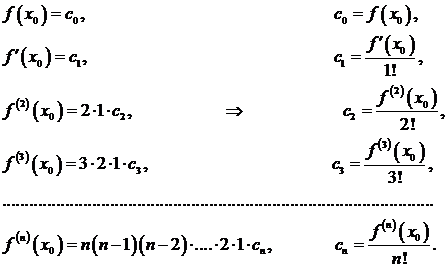
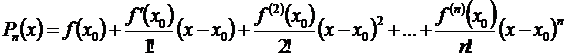 . (3.46)
. (3.46)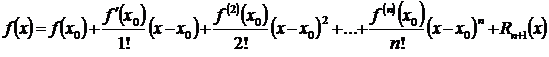 . (3.47)
. (3.47)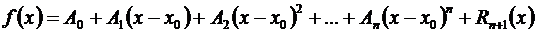 ,
,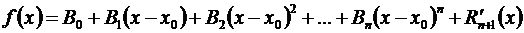 ,
,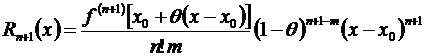 , (3.48)
, (3.48)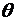 – число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.
– число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.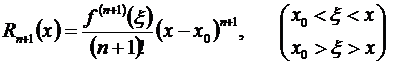 . (3.49)
. (3.49)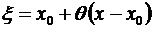 .
.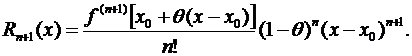 (3.50)
(3.50)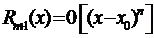 . (3.51).
. (3.51).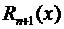 представляет собой бесконечно малую порядка выше n -го по сравнению с (х – х 0), т.е.
представляет собой бесконечно малую порядка выше n -го по сравнению с (х – х 0), т.е. 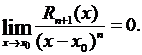 Равенство (3.51) называют остаточным членом, представленным в форме Пеано.
Равенство (3.51) называют остаточным членом, представленным в форме Пеано.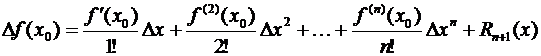 (3.52)
(3.52)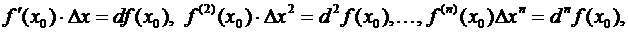
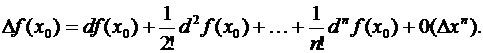
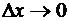 последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно
последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно 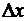 ) в разложении бесконечно малого приращения функции.
) в разложении бесконечно малого приращения функции.


