В этом разделе будет изложен способ воспроизведения функциональной зависимости между двумя переменными величинами х и у с помощью полинома.
Пусть в результате измерений в некотором опыте или наблюдении получены при разных значениях переменной величины 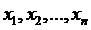 (далее будем считать, что эти значения переменной величины пронумерованы в порядке возрастания, т.е.
(далее будем считать, что эти значения переменной величины пронумерованы в порядке возрастания, т.е. 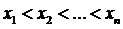 ) соответствующие значения переменной величины
) соответствующие значения переменной величины 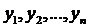 . Это соответствие можно представить в виде таблицы
. Это соответствие можно представить в виде таблицы
Эту таблицу можно изобразить также и в виде n точек геометрического пространства 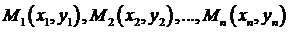 , для которых упорядоченные пары (хi, yi), i = 1,2, …, n являются координатами этих точек в прямоугольной системе координат. Данную таблицу можно рассматривать как задание некоторой функциональной зависимости y = f (x) между переменными величинами х и у. Возникает задача воспроизведения функциональной зависимости y = f (x) между переменными величинами х и у в аналитическом виде.
, для которых упорядоченные пары (хi, yi), i = 1,2, …, n являются координатами этих точек в прямоугольной системе координат. Данную таблицу можно рассматривать как задание некоторой функциональной зависимости y = f (x) между переменными величинами х и у. Возникает задача воспроизведения функциональной зависимости y = f (x) между переменными величинами х и у в аналитическом виде.
Аналитическое выражение этой зависимости y = f (x) будем искать среди функций наиболее простого вида – полиномов. Искомый полином 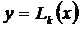

должен удовлетворять условиям
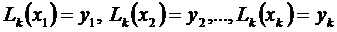 , (3.54)
, (3.54)
т.е. график его должен проходить через точки 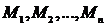 (рис.21).
(рис.21).
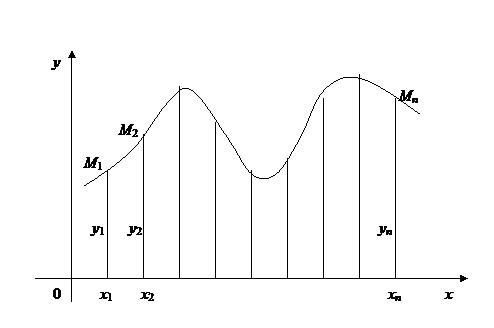
Рис. 21
Из этих условий, представляющих собой систему п уравнений можно определить п коэффициентов полинома, а потому Lk (x) является полиномом степени, не выше, чем 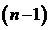 , т.е. k ≤
, т.е. k ≤ 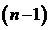 :
:
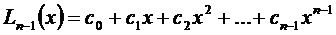 . (3.55)
. (3.55)
После того, когда коэффициенты, а, следовательно, и сам полином будут найдены, то тогда можно приближенно находить значение функции (т.е. устанавливать соответствие между переменными величинами х и у) в точках х,которые лежат между точками x 1, x 2, …, xn.
Нахождение значений функции у = 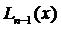 для значений аргумента х,которые лежат между точками x 1, x 2, …, xn ,называется интерполяцией; числа x 1, x 2, …, xn называются интерполяционными узлами, а полином
для значений аргумента х,которые лежат между точками x 1, x 2, …, xn ,называется интерполяцией; числа x 1, x 2, …, xn называются интерполяционными узлами, а полином 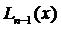 – интерполяционным полиномом.
– интерполяционным полиномом.
Чтобы найти интерполяционный полином 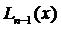 , надо найти его коэффициенты:
, надо найти его коэффициенты: 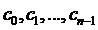 . Для нахождения этих n неизвестных коэффициентов в соответствии с условием (2), имеем систему n линейных уравнений
. Для нахождения этих n неизвестных коэффициентов в соответствии с условием (2), имеем систему n линейных уравнений
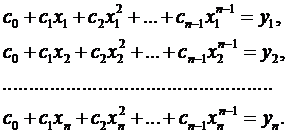 . (3.56)
. (3.56)
Так как согласно условию все интерполяционные узлы 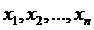 разные, поэтому определитель этой системы
разные, поэтому определитель этой системы
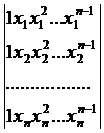
отличен от нуля (определитель Вандермонда). Следовательно, система совместна и имеет единственное решение при любых значениях уi (i = 1,2,… n) в правых частях системы (система Крамера), т.е. коэффициенты интерполяционного многочлена 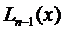 находятся однозначно. Находя коэффициенты
находятся однозначно. Находя коэффициенты 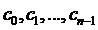 , из системы (3.56) и подставляя их значение в (3.55), получим искомый интерполяционный полином
, из системы (3.56) и подставляя их значение в (3.55), получим искомый интерполяционный полином 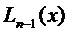 .
.
Пример. Построить полином не выше второй степени, который бы в точках x 1 = –1, x 2 = 0, x 3 = 3 приобретал бы, соответственно, значения y 1 = 13, y 2 = 6, y 3 = 9. Другими словами, искомый полином 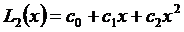
должен быть построен в соответствии с таблицей
Для нахождения неизвестных коэффициентов 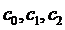 , аналогично общему случаю (3.56) получаем систему уравнений
, аналогично общему случаю (3.56) получаем систему уравнений
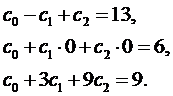 (3.57)
(3.57)
Из второго уравнения этой системы сразу находим c 0 = 6.
Подставляя это значение с 0 в другие два уравнения системы (3.57) и сделав упрощения, приходим к системе двух линейных уравнений с двумя неизвестными
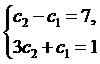
и отсюда получаем 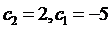 . Таким образом, искомый полином
. Таким образом, искомый полином
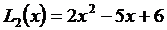 .
.
Действительно,
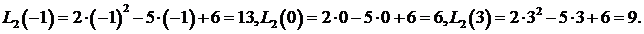
Хотя этот способ нахождения интерполяционного полинома 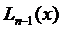 можно использовать во всех случаях, однако если число n большое, то решение системы (3.56) делается громоздким и занимает много времени.
можно использовать во всех случаях, однако если число n большое, то решение системы (3.56) делается громоздким и занимает много времени.
Существует другой способ нахождения полинома 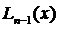 , указанный Лагранжем, в котором нет необходимости решать систему уравнений (3.56).
, указанный Лагранжем, в котором нет необходимости решать систему уравнений (3.56).
Пусть соответствие между значениями переменных величин х и у задается таблицей
| x
| x 1
| x 2
| x 3
| …
| xk
| …
| …
| xn
|
| y
| y 1
| y 2
| y 3
| …
| yk
| …
| …
| yn
|
Необходимо построить интерполяционный полином 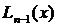 , степени не больше n – 1 и для которого выполнены условия
, степени не больше n – 1 и для которого выполнены условия
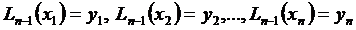 . (3.58)
. (3.58)
Будем искать полином 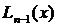 в виде
в виде
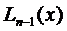 = y 1 l 1(x) + y 2 l 2(x) +…+ yklk (x) +…+ ynln (x), (3.59)
= y 1 l 1(x) + y 2 l 2(x) +…+ yklk (x) +…+ ynln (x), (3.59)
где lk (x), k = 1,2, …, n – полиномы степени не выше n – 1 и свойства, которых можно выразить так: в интерполяционном узле х = хk полином lk (xk) равняется 1, а в других узлах lk (xj), где 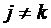 равняется нулю. Иначе говоря
равняется нулю. Иначе говоря
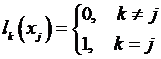 (3.60)
(3.60)
причем 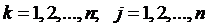 . Требование (3.60) совместно с (3.59) обеспечивает выполнение условий (3.58).
. Требование (3.60) совместно с (3.59) обеспечивает выполнение условий (3.58).
Полиномы lk (x) составим следующим образом:
lk (x) = 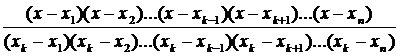 .
.
В числителе у этих полиномов отсутствует множитель (x – xk), а в знаменателе – (xk – xk) для всех k = 1,2, …, n.
Легко убедиться, что данные полиномы есть полиномы степени не выше n – 1 и удовлетворяют требованию (3.60). Теперь подставляя их в (3.59) получим искомый полином
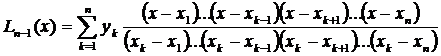 ,
,
который дает решение поставленной задачи и называется интерполяционным полиномом Лагранжа.
Представим интерполяционный полином Лагранжа в более компактном виде. Для этого введем полином 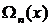 , который определяется равенством
, который определяется равенством
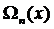 = (х – х 1)(х – х 2)…(х – хk- 1)(х – хk)(х – хk+ 1)…(х – хn).
= (х – х 1)(х – х 2)…(х – хk- 1)(х – хk)(х – хk+ 1)…(х – хn).
Продифференцируем этот полином 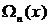 по х:
по х:
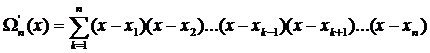 .
.
При x = xk (k = 1,2,…, n) имеем
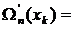 (хk – х 1)(хk – х 2)…(хk – хk- 1)(хk – хk+ 1)…(хk – хn).
(хk – х 1)(хk – х 2)…(хk – хk- 1)(хk – хk+ 1)…(хk – хn).
Тогда интерполяционный полином Лагранжа примет вид
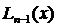 =
= 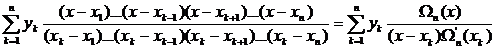 .
.
Окончательно
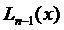 =
= 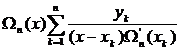 . (3.61)
. (3.61)
В качестве примера рассмотрим два частных случая полинома Лагранжа.
При n = 2 имеем две точки (х 1, у 1) и (х 2, у 2), и полином Лагранжа представляет в этом случае уравнение прямой 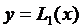 , проходящей через две эти точки:
, проходящей через две эти точки:
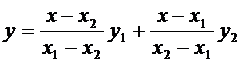 .
.
При n = 3 получим уравнение параболы 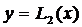 , проходящей через три точки (х 1, у 1), (х 2, у 2) и (х 3, у 3):
, проходящей через три точки (х 1, у 1), (х 2, у 2) и (х 3, у 3):
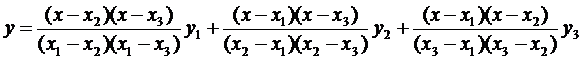 .
.
Аппроксимация функций
В этом разделе наряду с формулой Тейлора будет изложен еще один способ приближенного изображения (аппроксимации) функции с помощью полинома.
Пусть функция у = f (x) заданна на промежутке [ a, b ]. Выделим здесь произвольно п интерполяционных узлов x 1, x 2,…, xn.
Построим интерполяционный полином Лагранжа 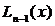 степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f (х), т.е.
степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f (х), т.е.
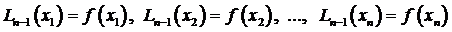 . (3.62)
. (3.62)
Интерполяционный полином Лагранжа 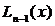 определяется равенством (3.61)
определяется равенством (3.61)
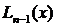 =
= 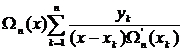 =
= 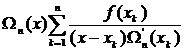 . (3.63)
. (3.63)
Свойства полинома Лагранжа 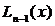 , выраженные равенствами (3.62), геометрически означают, что график полинома Лагранжа у =
, выраженные равенствами (3.62), геометрически означают, что график полинома Лагранжа у = 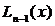 (рис.22, пунктирная кривая) имеет в интерполяционных узлах x 1, x 2,…, xn такие же ординаты, что и график функции y = f (x) (рис.22, сплошная кривая).
(рис.22, пунктирная кривая) имеет в интерполяционных узлах x 1, x 2,…, xn такие же ординаты, что и график функции y = f (x) (рис.22, сплошная кривая).
Поскольку полином Лагранжа 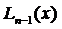 принимают за приближенное выражение для f (x),возникает потребность найти ошибку
принимают за приближенное выражение для f (x),возникает потребность найти ошибку 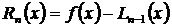 приближенного равенства
приближенного равенства 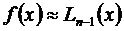 .
.
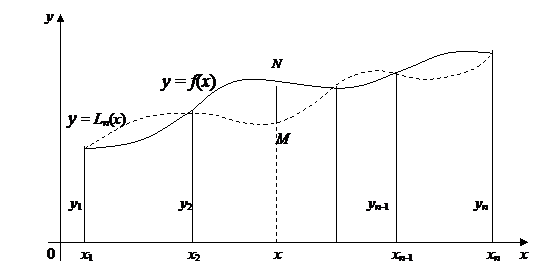
Рис. 22
Геометрическое значение 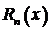 такое же, как и для остаточного члена формулы Тейлора:
такое же, как и для остаточного члена формулы Тейлора: 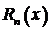 есть отрезок ординаты МN,расположенный между графиками функции f (х) и полинома
есть отрезок ординаты МN,расположенный между графиками функции f (х) и полинома 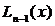 в точке х,взятой со знаком плюс, если график f (х) в точке х проходит выше графика
в точке х,взятой со знаком плюс, если график f (х) в точке х проходит выше графика 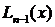 (рис.22), и со знаком минус, если ниже.
(рис.22), и со знаком минус, если ниже.
Теорема. Пусть на промежутке [ a, b ] для функции f (x)существуют последовательные производные 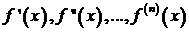 и пусть интерполяционные узлы
и пусть интерполяционные узлы 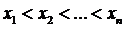 лежат в промежутке [ a, b ]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [ a, b ],что выполняется равенство
лежат в промежутке [ a, b ]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [ a, b ],что выполняется равенство
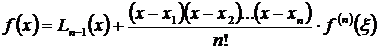 (3.64)
(3.64)
для всех х,которые лежат в промежутке [ a, b ].
Доказательство. Пусть точка х зафиксирована на промежутке [ a, b ] и не совпадает ни с одним из интерполяционных узлов. Рассмотрим вспомогательную функцию
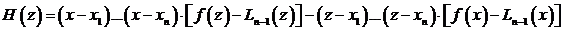 . (3.65)
. (3.65)
При этих условиях вспомогательная функция Н (z) имеет на [ a, b ] (n + 1) корней и будет обращаться в нуль на концах каждого из отрезков 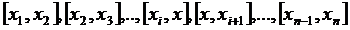 ,
,
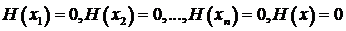 . (3.66)
. (3.66)
Применяя теорему Роля к каждому из этих отрезков убеждаемся, что производная 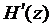 , имеет не менее п корней в п разных точках
, имеет не менее п корней в п разных точках 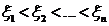 ,
,
расположенных внутри отрезков 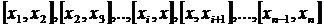 ,таких что
,таких что 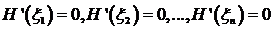 .
.
Применив теорему Ролля к производной 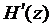 , мы убеждаемся, что производная
, мы убеждаемся, что производная 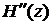 имеет п – 1 корней на [ a, b ]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [ a, b ] производная
имеет п – 1 корней на [ a, b ]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [ a, b ] производная 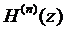 имеет хотя бы один корень, который обозначим через
имеет хотя бы один корень, который обозначим через 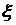 , т.е.
, т.е.
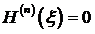 . (3.67)
. (3.67)
Найдем из (3.65) 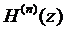 . Учитывая, что
. Учитывая, что 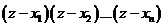 – полином степени п,а тогда, как установлено ранее,
– полином степени п,а тогда, как установлено ранее, 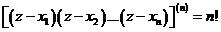 , имеем
, имеем
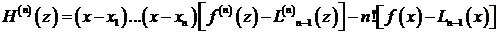 . (3.68)
. (3.68)
Далее, степень полинома 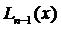 не выше п – 1, и потому
не выше п – 1, и потому 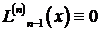 . Следовательно
. Следовательно
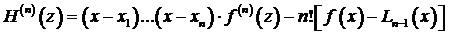 .
.
Отсюда находим
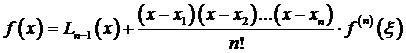 . (3.69)
. (3.69)
Причем, ξ не совпадает с узлами x 1, x 2,…, xn и точкой х. Теорема доказана.
Равенство (3.69) называется интерполяционной формулой Лагранжа с остаточным членом. Остаточный член Rn (x)в этой формуле определяется равенством
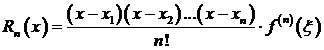 .
.
Отсюда, если известна верхняя граница 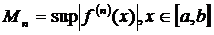 ,
,
получим оценку для абсолютной погрешности вычисления значений функции f (х) с использованием интерполяционной формулы Лагранжа
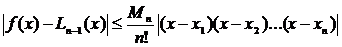 .
.
Из полученной оценки следует, что чем больше используется интерполяционных узлов, тем выше точность вычисления.
Пример. Функцию
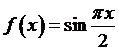 (3.70)
(3.70)
аппроксимировать с помощью интерполяционного полинома Лагранжа 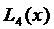 , который, в пяти узлах
, который, в пяти узлах 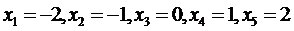 приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.
приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.
Прежде всего, вычислим значения этой функции в интерполяционных узлах. Из (3.70) находим
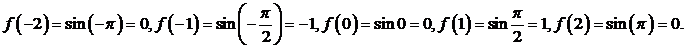 Следовательно, полином
Следовательно, полином  должен быть построен по таблице
должен быть построен по таблице
Поэтому
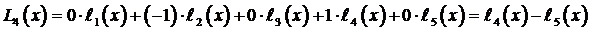 .
.
Для 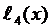 и
и 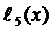 имеем
имеем
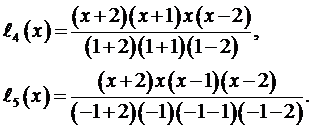
Таким образом,
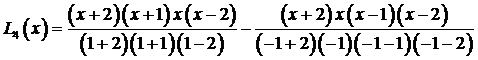
и после упрощений получаем 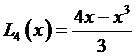 .
.
Далее, для остаточного члена R 5(x)нужно вычислить 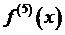 .
.
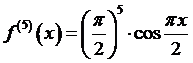 .
.
Поэтому для функции 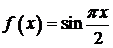 этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
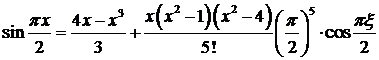 .
.
Если для вычисления значений функции 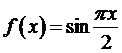 пользоваться приближенной формулой
пользоваться приближенной формулой 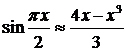 , то абсолютная погрешность такого вычисления, учитывая, что |
, то абсолютная погрешность такого вычисления, учитывая, что | 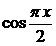 | ≤ 1 составит
| ≤ 1 составит
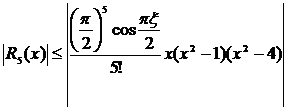
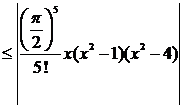 .
.
Так, для 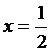 абсолютная погрешность вычисления составит
абсолютная погрешность вычисления составит
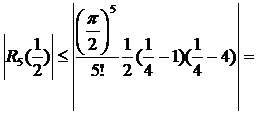 0,11.
0,11.
На рис.23 изображены графики функции 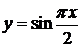 (сплошная кривая) и интерполяционного полинома
(сплошная кривая) и интерполяционного полинома 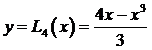 (пунктирная кривая).
(пунктирная кривая).
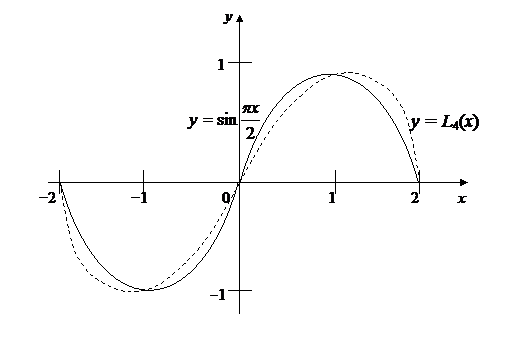
Рис. 23
Отметим, что 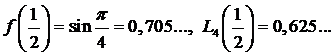 и абсолютная погрешность аппроксимации составляет 0,08.
и абсолютная погрешность аппроксимации составляет 0,08.
Для достижения более высокой точности вычисления необходимо
увеличивать число интерполяционных узлов.



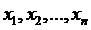 (далее будем считать, что эти значения переменной величины пронумерованы в порядке возрастания, т.е.
(далее будем считать, что эти значения переменной величины пронумерованы в порядке возрастания, т.е. 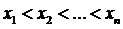 ) соответствующие значения переменной величины
) соответствующие значения переменной величины 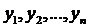 . Это соответствие можно представить в виде таблицы
. Это соответствие можно представить в виде таблицы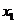
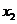
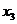
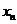
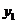
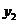
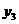
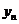
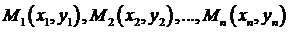 , для которых упорядоченные пары (хi, yi), i = 1,2, …, n являются координатами этих точек в прямоугольной системе координат. Данную таблицу можно рассматривать как задание некоторой функциональной зависимости y = f (x) между переменными величинами х и у. Возникает задача воспроизведения функциональной зависимости y = f (x) между переменными величинами х и у в аналитическом виде.
, для которых упорядоченные пары (хi, yi), i = 1,2, …, n являются координатами этих точек в прямоугольной системе координат. Данную таблицу можно рассматривать как задание некоторой функциональной зависимости y = f (x) между переменными величинами х и у. Возникает задача воспроизведения функциональной зависимости y = f (x) между переменными величинами х и у в аналитическом виде.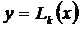

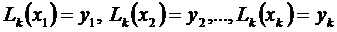 , (3.54)
, (3.54)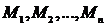 (рис.21).
(рис.21).
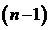 , т.е. k ≤
, т.е. k ≤ 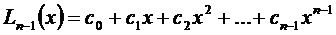 . (3.55)
. (3.55)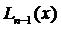 для значений аргумента х,которые лежат между точками x 1, x 2, …, xn ,называется интерполяцией; числа x 1, x 2, …, xn называются интерполяционными узлами, а полином
для значений аргумента х,которые лежат между точками x 1, x 2, …, xn ,называется интерполяцией; числа x 1, x 2, …, xn называются интерполяционными узлами, а полином 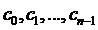 . Для нахождения этих n неизвестных коэффициентов в соответствии с условием (2), имеем систему n линейных уравнений
. Для нахождения этих n неизвестных коэффициентов в соответствии с условием (2), имеем систему n линейных уравнений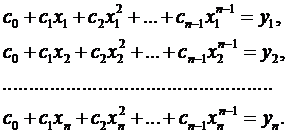 . (3.56)
. (3.56)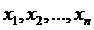 разные, поэтому определитель этой системы
разные, поэтому определитель этой системы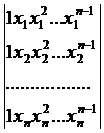
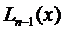 находятся однозначно. Находя коэффициенты
находятся однозначно. Находя коэффициенты 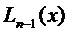 .
.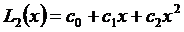
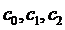 , аналогично общему случаю (3.56) получаем систему уравнений
, аналогично общему случаю (3.56) получаем систему уравнений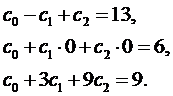 (3.57)
(3.57)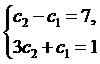
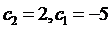 . Таким образом, искомый полином
. Таким образом, искомый полином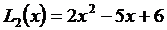 .
.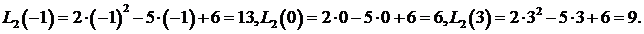
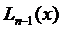 можно использовать во всех случаях, однако если число n большое, то решение системы (3.56) делается громоздким и занимает много времени.
можно использовать во всех случаях, однако если число n большое, то решение системы (3.56) делается громоздким и занимает много времени.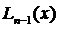 , указанный Лагранжем, в котором нет необходимости решать систему уравнений (3.56).
, указанный Лагранжем, в котором нет необходимости решать систему уравнений (3.56).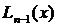 , степени не больше n – 1 и для которого выполнены условия
, степени не больше n – 1 и для которого выполнены условия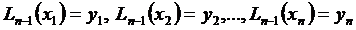 . (3.58)
. (3.58)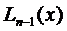 = y 1 l 1(x) + y 2 l 2(x) +…+ yklk (x) +…+ ynln (x), (3.59)
= y 1 l 1(x) + y 2 l 2(x) +…+ yklk (x) +…+ ynln (x), (3.59)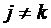 равняется нулю. Иначе говоря
равняется нулю. Иначе говоря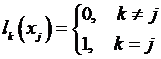 (3.60)
(3.60)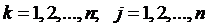 . Требование (3.60) совместно с (3.59) обеспечивает выполнение условий (3.58).
. Требование (3.60) совместно с (3.59) обеспечивает выполнение условий (3.58).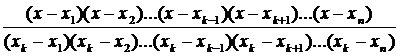 .
.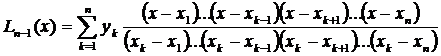 ,
,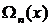 , который определяется равенством
, который определяется равенством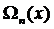 = (х – х 1)(х – х 2)…(х – хk- 1)(х – хk)(х – хk+ 1)…(х – хn).
= (х – х 1)(х – х 2)…(х – хk- 1)(х – хk)(х – хk+ 1)…(х – хn). по х:
по х: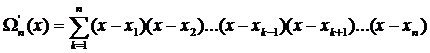 .
.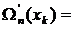 (хk – х 1)(хk – х 2)…(хk – хk- 1)(хk – хk+ 1)…(хk – хn).
(хk – х 1)(хk – х 2)…(хk – хk- 1)(хk – хk+ 1)…(хk – хn).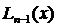 =
= 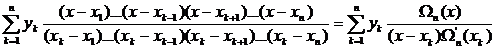 .
.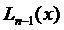 =
= 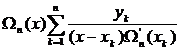 . (3.61)
. (3.61)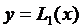 , проходящей через две эти точки:
, проходящей через две эти точки: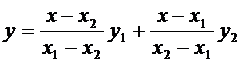 .
.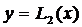 , проходящей через три точки (х 1, у 1), (х 2, у 2) и (х 3, у 3):
, проходящей через три точки (х 1, у 1), (х 2, у 2) и (х 3, у 3):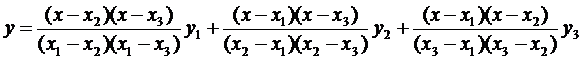 .
. степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f (х), т.е.
степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f (х), т.е. . (3.62)
. (3.62)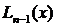 =
= 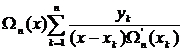 =
= 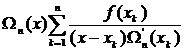 . (3.63)
. (3.63)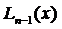 принимают за приближенное выражение для f (x),возникает потребность найти ошибку
принимают за приближенное выражение для f (x),возникает потребность найти ошибку 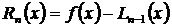 приближенного равенства
приближенного равенства 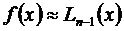 .
.
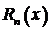 такое же, как и для остаточного члена формулы Тейлора:
такое же, как и для остаточного члена формулы Тейлора: 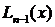 (рис.22), и со знаком минус, если ниже.
(рис.22), и со знаком минус, если ниже.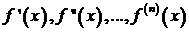 и пусть интерполяционные узлы
и пусть интерполяционные узлы 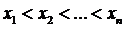 лежат в промежутке [ a, b ]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [ a, b ],что выполняется равенство
лежат в промежутке [ a, b ]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [ a, b ],что выполняется равенство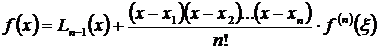 (3.64)
(3.64)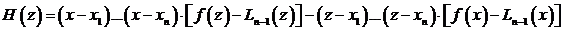 . (3.65)
. (3.65)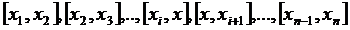 ,
,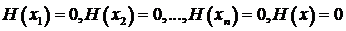 . (3.66)
. (3.66)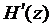 , имеет не менее п корней в п разных точках
, имеет не менее п корней в п разных точках 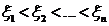 ,
,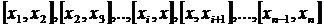 ,таких что
,таких что 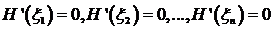 .
.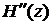 имеет п – 1 корней на [ a, b ]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [ a, b ] производная
имеет п – 1 корней на [ a, b ]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [ a, b ] производная 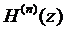 имеет хотя бы один корень, который обозначим через
имеет хотя бы один корень, который обозначим через 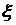 , т.е.
, т.е.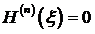 . (3.67)
. (3.67)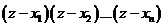 – полином степени п,а тогда, как установлено ранее,
– полином степени п,а тогда, как установлено ранее, 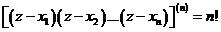 , имеем
, имеем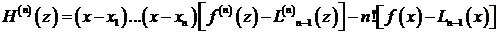 . (3.68)
. (3.68)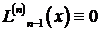 . Следовательно
. Следовательно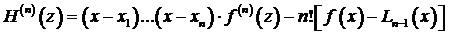 .
.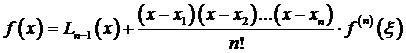 . (3.69)
. (3.69)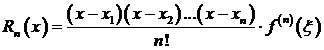 .
.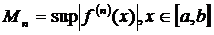 ,
,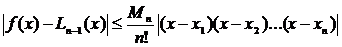 .
.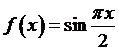 (3.70)
(3.70)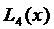 , который, в пяти узлах
, который, в пяти узлах 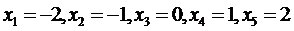 приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.
приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.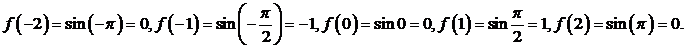 Следовательно, полином
Следовательно, полином 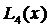 должен быть построен по таблице
должен быть построен по таблице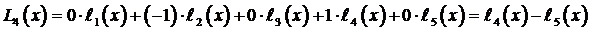 .
.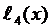 и
и 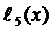 имеем
имеем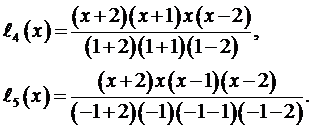
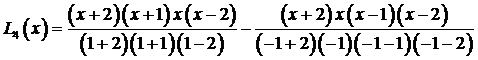
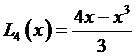 .
.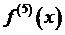 .
.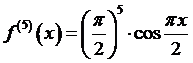 .
.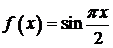 этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом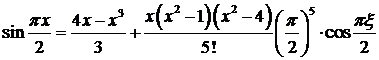 .
.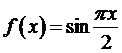 пользоваться приближенной формулой
пользоваться приближенной формулой 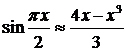 , то абсолютная погрешность такого вычисления, учитывая, что |
, то абсолютная погрешность такого вычисления, учитывая, что | 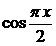 | ≤ 1 составит
| ≤ 1 составит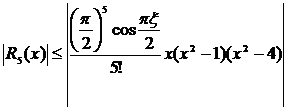
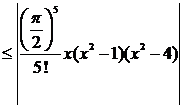 .
.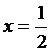 абсолютная погрешность вычисления составит
абсолютная погрешность вычисления составит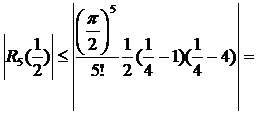 0,11.
0,11.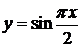 (сплошная кривая) и интерполяционного полинома
(сплошная кривая) и интерполяционного полинома 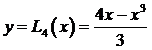 (пунктирная кривая).
(пунктирная кривая).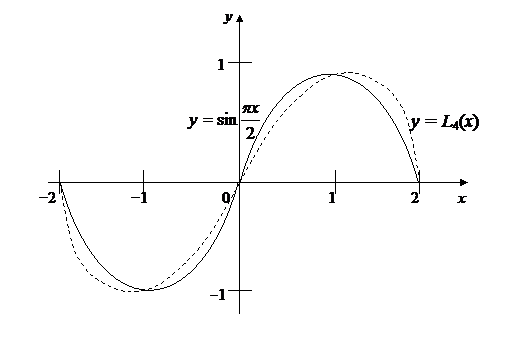
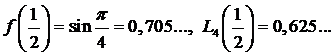 и абсолютная погрешность аппроксимации составляет 0,08.
и абсолютная погрешность аппроксимации составляет 0,08.


