Если f(x) непрерывна на [а,b] и F(x) первообразная для f(x),то имеет место формула Ньютона- Лейбница.

Из Т1,т.к. 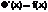 , то Ф(х)-первообразная для f(x),т.к. F(x) другая первообразная, то Ф(х)= F(x)+С или
, то Ф(х)-первообразная для f(x),т.к. F(x) другая первообразная, то Ф(х)= F(x)+С или
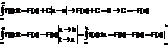
Замена переменной в определенном интеграле

Интегрирование по частям определенного интеграла

Обозначим

35. Несобственные интегралы с бесконечными пределами (1-го рода) и несобственные интегралы от неограниченных функций (2-го рода).
Несобственные интегралы 1-го рода
Другое название несобственных интегралов 1-го рода: интегралы с бесконечными пределами.
Несобственный интеграл от функции f(x) в пределах от a до + 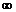 определяется равенством:
определяется равенством:
 =
= 
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует или равен бесконечности – расходящимся. Аналогично:
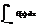 =
= 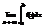 ,
,
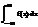 =
= 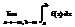 .
.
Несобственные интегралы 2-го рода
Другое название несобственных интегралов 2-го рода: интегралы от разрывных (неограниченных) функций.
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a;b] и непрерывна при a≤  <c и c<x≤b, то несобственный интеграл второго рода определяется равенством:
<c и c<x≤b, то несобственный интеграл второго рода определяется равенством:
 =
=
= 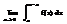 +
+
+  (1)
(1)
Несобственный интеграл (1) (где f(c) = 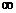 ,a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.
,a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.
Вопрос 27 Условный экстремум. Наибольшее и наименьшее значения функции двух переменных в замкнутой области.
Условный экстремум.
Пусть, где φi — функции, заданные на. Тогда точка называется точкой условного экстремума функции f, заданной на относительно ограничений φi(x) = 0 если она является точкой обычного экстремума на множестве E.
Условный экстремум
Пусть функция
u = f(x1, x2, …, xn)
(1)
определена в некоторой области D М Rn и ее аргументы не являются независимыми переменными, а связаны k (k<n) соотношениями:
Fi(x1, x2, …, xn) = 0 (i = 1,2, …,k).
(2)
Условия (2) называются уравнениями связи.
Пусть координаты точки M0(x10, …,xn0) О D удовлетворяют уравнениям связи (2).
Точка M0(x10, …,xn0) называется точкой условного максимума (минимума) функции (1) при условиях связи (2), если существует такая окрестность Oδ(M0) точки M0, что для любой точки M(x1, …,xn) О Oδ(M0), координаты которой удовлетворяют уравнениям связи (2), выполняется неравенство f(M) ≤ f(M0) (f(M) ≥ f(M0)).
Методы нахождения условного экстремума
Метод исключения переменных
Ограничимся для простоты случаем n = 2, k = 1, т.е. нахождением условного экстремума функции 2–х переменных.
Пусть функция z = f(x,y) определена в некоторой области D М R2 и ее аргументы связаны условием
F(x,y) = 0.
(3)
Допустим, что уравнение (3) определяет неявно функцию y(x). Тогда можно рассматривать сложную функцию f(x,y(x)) = u(x). Если эта функция имеет экстремум в точке x0 и y(x0) = y0, то точка (x0,y0) является точкой условного экстремума функции f(x,y), аргументы которой удовлетворяют уравнению связи (3).
Если уравнение связи (3) можно разрешить относительно y и перейти от неявного задания функции y(x) к явному, то отыскание условных экстремумов в рассматриваемом случае сводится к отысканию обычных (безусловных) экстремумов функции y(x).
Метод неопределенных множителей Лагранжа
Пусть функции f(x1, x2, …, xn) и Fi(x1, x2, …, xn) (i = 1,2, …,k) дифференцируемы в некоторой области D М Rn. Тогда задача отыскания точек условного экстремума функции f(x1, x2, …, xn) при условиях связи
Fi(x1, x2, …, xn) = 0 (i = 1,2, …,k).
эквивалентна задаче о нахождении точек обычного (безусловного) экстремума функции Лагранжа:
L(x1,x2,:::,xn; λ1,λ2,:::,λk) = f(x1,x2,:::,xn) + λ1 · F1(x1,x2,:::,xn) +
+ λ2 · F2(x1,x2,:::,xn) + … + λk · Fk(x1,x2,:::,xm).
(4)
Схема метода Лагранжа:
1. Составляем функцию Лагранжа (4).
2. Для отыскания стационарных точек функции Лагранжа находим ее частные производные по всем аргументам
∂L
∂x1
= ∂f
∂x1
+ λ1 · ∂F1
∂x1
+ … + λk · ∂Fk
∂x1
,
… … … … …
∂L
∂xn
= ∂f
∂xn
+ λ1 · ∂F1
∂xn
+ … + λk · ∂Fk
∂xn
,
… … … … …
∂L
∂λ1
= F1(x1, x2, …, xn),
… … … … …
∂L
∂λk
= Fk(x1, x2, …, xn)
и приравниваем их к нулю.
Получаем систему (n + k) уравнений с (n + k) неизвестными:
∂f
∂x1
+ λ1 · ∂F1
∂x1
+ … + λk · ∂Fk
∂x1
= 0,
… … … … …
∂f
∂xn
+ λ1 · ∂F1
∂xn
+ … + λk · ∂Fk
∂xn
= 0,
… … … … …
F1(x1, x2, …, xn) = 0,
… … … … …
Fk(x1, x2, …, xn) = 0.
Если (x10,:::,xn0; λ10,:::,λk0) — решение этой системы, то оно определяет стационарную точку (x10,:::,xn0) функции f(x1,x2,:::,xn) при условиях связи (2), в которой функция может иметь условный экстремум.
3. Чтобы установить наличие или отсутствие условного экстремума в каждой стационарной точке M0, нужно исследовать знак 2–го дифференциала функции Лагранжа
d2L(M0) = n ∂2L
∂xi∂xj
(M0) dxidxj
∑
i, j = 1
при значениях дифференциалов dx1, …,dxn, не равных одновременно нулю и удовлетворяющих продифференцированным уравнениям связи
∂fi(M0)
∂x1
dx1 + … + ∂fi(M0)
∂xn
dxn = 0, i = 1,
…,k.
Замечание. При решении практических задач во многих случаях наличие условного экстремума в стационарной точке определяется существом задачи.
Обоснование метода Лагранжа для случая n = 2, k = 1 приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М.: Изд–во МЭИ, 2002 (стр. 170).
Геометрический смысл условного экстремума функции:
Условными экстремумами функции z = f(x,y) при F(x,y) = 0 являются ее экстремумы на линии, образующейся в сечении поверхности z = f(x,y) цилиндрической поверхностью F(x,y) = 0.
¾¾¾¾ * * * ¾¾¾¾




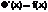 , то Ф(х)-первообразная для f(x),т.к. F(x) другая первообразная, то Ф(х)= F(x)+С или
, то Ф(х)-первообразная для f(x),т.к. F(x) другая первообразная, то Ф(х)= F(x)+С или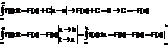



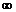 определяется равенством:
определяется равенством: =
= 
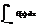 =
= 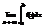 ,
,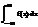 =
= 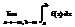 .
. <c и c<x≤b, то несобственный интеграл второго рода определяется равенством:
<c и c<x≤b, то несобственный интеграл второго рода определяется равенством: =
=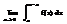 +
+ (1)
(1)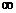 ,a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.
,a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.


