y=f(x) и y=g(x) б.м. при х→а, т.е. 
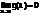
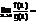 0, f(x) б.м. более высокого порядка, чем g(x), обозн. f(x)=0g(x)
0, f(x) б.м. более высокого порядка, чем g(x), обозн. f(x)=0g(x)
∞, g(x) более высокого порядка, чем f(x)
C, f(x) и g(x) б.м. одного порядка
1, f (x) и g(x) – б.м. эквивалентные f(x) ~ g(x)
Не существует. f(x), g(x), несравнимые б.м.
Если  , то f(x) б.м. к-ого порядка, относительно g(x)
, то f(x) б.м. к-ого порядка, относительно g(x)
Теорема 1: α~βó α-β=0(α), α-β=0(β),
Следствие: α~βó α=β+0(α), α=β+0(β),
Определение: представление ф-ции f(x) в виде
f(x)= A* xk+0(xk) назыв. выделением её главной части.
Теорема2: α~β, а β~γ, то α~γ
Теорема 3: α~α1 и β~β1 то 1) lim α/β= lim α1/β1=
lim α/β1= lim α1/β
2) lim αβ=lim α1β1 = lim αβ1 = lim α1β
Теорема4: алгебрарическая сумма, конечного числа б.м. эквивалентна слагаемому низшего порядка.  сумма бесконечно малых, α низшего порядка, α – главная часть этой суммы
сумма бесконечно малых, α низшего порядка, α – главная часть этой суммы
Следствие: 
Непрерывность ф-ции. Точки разрыва. Их классификация.
y=f(x), x0
x0→x, x-x0=∆x, приращение аргумента в т. X,
x =x0+∆x; f(x)-f(x0)=∆y – приращение ф-ции в т.x0
∆y=f(x0 + x)-f(x0)
Опр. Ф-я y=f(x) наз. непрерывной в т. х0, если lim(∆x→0) y=0 (1),
(1) →lim(∆x→0) [f(x0 +0x)-f(x0)]=0
(2) →lim(x→x 0) f(x)=f(x0)
(1) и (2) – эквивалентные определения непрерывности
f(x0 -0)+f(x0 +0) →f(x0) (3)
Из предыдущего ясно, что если f(x) непрерывна в т. x0, то выполняется рав-во (3)
Докажем, что у=sinx непрерывна для всех х: lim(∆x→0)∆y =lim(∆x→0) [sin(x0 +∆x)-sinx0 ] =lim(∆x→0) (sinx0cos∆x+cosx0sin∆x-sinx0)=lim(∆x→0) (sinx0 –sinx0)=0
Опр. Ф-я y=f(x) непрерывна в интервале (а,b) если она непрерывна во всех т-ках этого интервала.
Ф-я y=f(x) непрерывна на отрезке (а,b) если она непрерывна во всех внутренних т-ках этого отрезка, а так же непрерывна справа в т. а(т.е сущ. lim(∆x→0) f(x)=f(a)) и непрерывна слева в т.b (т.е lim(∆x→0) f(x)=f(b)) Аналогично, как для sin можно док-ть, что все основные элементарные ф-ции непрерывны во всех областях, где они определены.
Точки разрыва.
Если для y=f(x) рав-во (3): f(x0 -0)+f(x0 +0) =f(x0) нарушается, то х0 - точка разрыва
Характер нарушения рав-ва (3) кладется в основу классификации точек разрыва:
1. а) если f(x0 -0) и f(x0 +0) сущ-ют и f(x0 -0) ≠f(x0 +0), то х0 - наз. т-кой разрыва 1-го рода с конечным скачком.
Разность f(x0 -0)-f(x0 +0) наз скачком ф-ции в т.х 0 b)Если в т. х f(x0 -0) = f(x0 +0) ≠f(x0), то х0 наз т-кой разрыва 1 рода устранимой.
2. Если хотя бы один из пределов f(x 0-0) или f(x0 +0) не сущ-ет или =∞, то х0 наз т-кой разрыва 2-го рода ф-ции y=f(x)
Теоремы о непрерывных ф-ях.
Т 1. Если y=f(x) и y=g(x) непрерывны в т. x 0, то в этой т-ке непрерывны также f(x) ±g(x), f(x)*g(x), f(x)/g(x),(g(x0) ≠0)
Т 2. Сложная ф-ция, составленная из конечного числа непрерывных ф-ций непрерывна.
Т 3. Ф-я обратная к непрерывной и монотонной ф-ции непрерывна.
Вывод: Все элементарные ф-ции непрерывны в областях, где они определены
Св-ва ф-ций непрерывных на отрезке
Т 1. Если ф-ция y=f(x) непрерывна на отрезке [а,b], то, по крайней мере, в одной т-ке этого отрезка она достигает наибольшее значение и, по крайней мере, в одной наименьшего, т.е
Ė x1?[a,b],что f(x1) ≥f(x), ¥ x?[a,b];
Ė x2?[a,b],что f(x2)≤ f(x), ¥ x?[a,b];

Т 2. Если f(x) непрерывна на [а,b], то она принимает все промежуточные значения между ее значениями на концах, т.е если f(a) ≠f(b),f(a)=A,f(b)=B
Пусть A<C<B,то Ė c? [а,b], что f(c)=c

Т 3. Если f(x) непрерывна на [а,b] и f(a) и f(b) разных знаков, то Ė c? [а,b], что f(c)=0

Дифференциальное исчисление одной переменной.
y=f(x), х?D(f), х+∆x?D(f)c→y-∆y=f(x+∆x)-f(x)
Опр. lim(∆x→0) ∆y/∆x наз производной данной ф-ции, (обозначается f ' (x), y ' x, dy/dx, df(x)/dx)
y'=lim(∆x→0) ∆y/∆x
y'=lim(∆x→0) (f(x+∆x)-f(x))/ ∆x




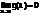
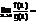 0, f(x) б.м. более высокого порядка, чем g(x), обозн. f(x)=0g(x)
0, f(x) б.м. более высокого порядка, чем g(x), обозн. f(x)=0g(x) , то f(x) б.м. к-ого порядка, относительно g(x)
, то f(x) б.м. к-ого порядка, относительно g(x) сумма бесконечно малых, α низшего порядка, α – главная часть этой суммы
сумма бесконечно малых, α низшего порядка, α – главная часть этой суммы






