

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Введенные нами дифференциальные операторы удобно представлять с помощью оператора Гамильтона, который обозначается символом 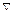 (набла) и рассматривается как символический вектор:
(набла) и рассматривается как символический вектор:
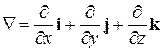 . (12)
. (12)
Правила действий с этим вектором таковы:
1. Произведение вектора 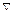 на скалярную функцию U (x,y,z) дает градиент этой функции
на скалярную функцию U (x,y,z) дает градиент этой функции
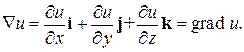 (13)
(13)
2. Скалярное произведение вектора 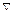 на векторную функцию А (x,y,z) дает дивергенцию этой функции
на векторную функцию А (x,y,z) дает дивергенцию этой функции
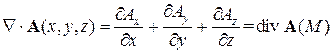 . (14)
. (14)
3. Векторное произведение вектора 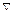 на векторную функцию А (x,y,z) дает ротор этой функции
на векторную функцию А (x,y,z) дает ротор этой функции
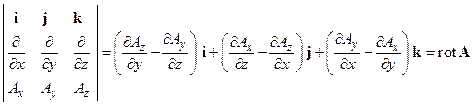 . (15)
. (15)
Перейдем теперь к наиболее важным для нас дифференциальным операторам второго порядка:
1. Оператор Лапласа, который образуется путем последовательного применения оператора градиента и оператора дивергенции к скалярной функции U (x,y,z). В результате получаем скалярную функцию
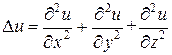 . (16)
. (16)
2. Оператор, представляющий собой последовательное применение оператора ротора и оператора дивергенции к скалярной функции U (x,y,z). Нетрудно убедиться, что в результате мы получим нулевой вектор:
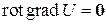 . (17)
. (17)
3. Оператор, представляющий собой последовательное применения оператора дивергенции и оператора ротора к векторной функции А (x,y,z). Нетрудно убедиться, что в этом случае мы в результате получим скаляр:
 . (18)
. (18)
Представленные выше операторы записаны в декартовой системе координат
4. При записи волновых уравнений иногда используют так называемый оператор Даламбера или волновой оператор
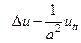 (19)
(19)
5. Оператор Δ u – вектор:
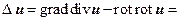
6. Оператор, представляющий собой последовательное применение оператора ротора и оператора дивергенции к скалярной функции U (x,y,z). Нетрудно убедиться, что в результате мы получим вектор, равный нулю, а именно:
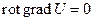 (20)
(20)
7. Оператор, представляющий собой последовательное применения оператора дивергенции и оператора ротора к векторной функции А (x,y,z). Нетрудно убедиться, что в этом случае мы в результате получим скалярную величину, равную нулю:
|
|
 (21)
(21)
В заключение заметим, что при записи уравнений в частных производных та часть, в которую входят частные производные, часто рассматривают как дифференциальный оператор. При этом используют запись L [ u ] или Lu, например
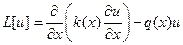
Г л а в а II. Одномерное волновое уравнение
К волновому уравнению, как уже отмечалось, мы приходим при изучении различных колебательных явлений, которые сопровождаются образованием волн (колебания точек струны, стержня, мембраны; колебания плотности, давления и скорости при распространении звука). В отсутствии внешних сил волновое уравнение имеет вид:
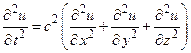 , (1)
, (1)
где с является постоянной скоростью распространения волны.
Мы начнем знакомство с волновым уравнением с одного из самых простых случаев, а именно с задачи о малых поперечных колебаниях струны без учета затухания.
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!