

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В. П. Трегубов
МАТЕМАТИЧЕСКАЯ ФИЗИКА
ДЛЯ ПРИКЛАДНЫХ МАТЕМАТИКОВ И ФИЗИКОВ
Курс лекций.
Часть I.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Санкт-Петербург
УДК 501 (517.946)
В. П. Трегубов
Математическая физика для прикладных математиков и физиков. Курс лекций.
Часть I. Дифференциальные уравнения математической физики. Изд-во СПбГУ, 2014,….с.
Курс лекций "Математическаяфизика для прикладных математиков и физиков" состоит из двух частей. В первой части "Уравнения математической физики" рассматриваются задачи математической физики, приводящие к уравнениям в частных производных, излагается вывод основных уравнений математической физики, а также основные методы решения этих уравнений.
Во второй части "Дополнительные главы математической физики" даётся описание специальных функций, интегральных уравнений Фредгольма и Вольтера, кинетических уравнений, обратных задач математической физики, а также некоторых численных методов решения уравнений математической физики.
В основу предлагаемого учебного пособия положены лекции, читаемые в Санкт-Петербургском университете, на факультете прикладной математики–процессов управлений для бакалавров по направлению "Прикладные математика и физика". При изложении материала автор старался опираться на физическую постановку задач, что определило и порядок изложения материала.
ОГЛАВЛЕНИЕ
Введение................................................................... 7
Предмет математической физики
Основные понятия и определения
Классификация квазилинейных уравнений второго порядка
Г л а в а I. Скалярные и векторные поля. Дифференциальные операторы
|
|
§ 1. Скалярные поля
§ 2. Векторные поля
§ 3. Оператор Гамильтона и дифференциальные операторы второго порядка
Г л а в а II. Одномерное волновое уравнение
§ 1. Уравнение малых поперечных колебаний струны
§ 2. Случай ограниченной струны
§ 3. Решение задачи Коши
Формула Даламбера
Частные случаи
Графическая интерпретация
§ 4. Метод характеристик
§ 5. Случай полубесконечной струны
§ 6. Метод разделения переменных для уравнения колебания ограниченной струны
Замечание о колебании музыкальных струн
§ 7. Вынужденные колебания струны, закрепленной на концах
§ 8. Продольные колебания однородного стержня
§ 9. Случай ненулевых граничных условий
§ 10. Телеграфное уравнение
§ 11. Общая схема метода разделения переменных для однородных
гиперболических уравнений
§ 12. Задача Гурса
§ 13. Теорема единственности решения краевых задач
для одномерного волнового уравнения
Г л а в а III. Двумерные и трехмерные задачи для волнового уравнения
§ 1. Волны в трехмерном пространстве
Сферически симметричная задача
Формула Пуассона
Физическая картина распространения волн в трехмерном пространстве
§ 2. Двумерное волновое уравнение
§ 3. Теорема единственности для двумерного волнового уравнения
§ 4. Трехмерное неоднородное волновое уравнение
§ 5. Точечный источник
§ 6. Уравнения малых поперечных колебаний мембраны
§ 7. Граничные условия.
§ 8. Решение задачи о колебаниях круглой мембраны
Г л а в аIV. Некоторые общие вопросы теории дифференциальных уравнений гиперболического типа
§ 1. Задача Коши. Характеристики.
§ 2. Слабый разрыв. Фронт волны
Г л а в а V. Уравнение теплопроводности и диффузии
§ 1. Уравнение теплопроволности для однородного стержня
§ 2. Граничные условия и их физический смысл
§ 3. Применение метода разделения переменных
§ 4. Задача о распространении тепла в изотропном твердом теле
§ 5. Уравнение диффузии
§ 6. Принцип максимального значения.
|
|
§ 7. Теорема единственности для неоднородного уравнения теплопроводности
Г л а в а VI. Стационарные задачи математической физики
§ 1. Уравнения Пуассона и Лапласа
Стационарное тепловое поле
Уравнения электростатики.
Потенциальное течение жидкости
§ 2. Оператор Лапласа в криволинейных координатах
§ 3. Фундаментальное решение уравнения Лапласа
§ 4. Гармонические функции.
§ 5. Формулы Грина
§ 6. Свойства гармонических функций
§ 7. Единственность решения краевых задач
Единственность и устойчивость решения задачи Дирихле
Теорема единственности для задачи Неймана
§ 8.Изолированные особые точки
§ 9. Регулярность гармонических функций на бесконечности
§ 10. Единственность решения внешнич краевыч задач
§ 11. Решение задачи Дирихле для уравнения Лапласа методом разделения
переменных.
Интегральная формула Пуассона
§ 11. Функция источника для уравнения Лапласа
§ 12. Решение задачи Дирихле в круге для уравнения Пуассона. Функция Грина.
Г л а в а VII. Теория потенциала
§ 1. Объемный потенциал
§ 2. Плоская задача. Логарифмический потенциал
§ 3. Потенциалы простого и двойного слоя
§ 5. Поверхности Ляпунова
§ 6. Разрывы потенциала двойного слоя.
§ 7. Поведение потенциала простого слоя при переходе через границу
§ 8. Применение поверхностных интегралов к решению краевых задач
§ 9. Задачи Дирихле для круга.
Г л а в а. V III. Уравнение Гельмгольца
§ 1. Связь уравнения Гельмгольца с уравнениями гиперболического и параболического типа
Установившиеся колебания мембраны.
Стационарные процессы диффузии газа при наличии распада и цепных реакций.
Диффузия в движущейся среде
§ 2. Внутренняя краевая задача
§ 3. Сферически симметричное решение уравнения Гельмгольца
в ограниченной области
§ 4. Сферически симметричное решение уравнения Гельмгольца
для неограниченной области
Г л а в а IX. Уравнения теории упругости
§ 1. Уравнения динамической теории упругости
§ 2. Скалярный и векторный потенциалы
Г л а в а X. Уравнения электромагнитного поля
§ 1. Система уравнений Лоренца-Максвелла
§ 2. Усреднённые уравнения Лоренца-Максвелла
Г л а в а XII. Уравнения гидродинамики и газовой динамики
§ 1. Течение идеальной жидкости
§ 2. Течение вязкой жидкости
Ньютоновские жидкости
Неньютоновские жидкости
|
|
§ 3. Постановка граничных условий
§ 4. Уравнения газовой динамики
§ 5. Закон сохранения энергии
§ 6. Звуковые колебания в жидкости и газе
Литература
 Введение
Введение
Скалярные поля
Цель этой короткой главы – лишь напомнить некоторые понятия, результаты, их математические формулировки и физический смысл, которые излагаются в курсе математического анализа, и которые потребуются нам в дальнейшем при изложении материала. Это касается понятий скалярного и векторного полей, а также дифференциальных операторов, применяемых к этим полям.
Наряду с понятием скалярной и векторной физической величины в математической физике часто пользуются понятиями скалярного поля и векторного поля.
Если в каждой точке М области D задано значение скалярной величины u, то эта величина является скалярной функцией точки, т.е. 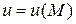 . В этом случае говорят, что в области D задано скалярное поле.
. В этом случае говорят, что в области D задано скалярное поле.
Для скалярного поля вводится понятие поверхности уровня, которая определяется как геометрическое место точек, в которых функция u имеет постоянное значение. В трехмерном случае это можно записать как
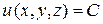 .
.
Градиент скалярной величины
Наряду с понятием поверхности уровня вводится понятие градиента, т.е. векторной величины, направление которой совпадает с направлением нормали к поверхности уровня скалярного поля (Рис. 1). Проекциями этого вектора на координатные оси служат частные производные от функции 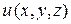

 , т. е.:
, т. е.:
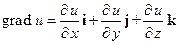 . (1)
. (1)
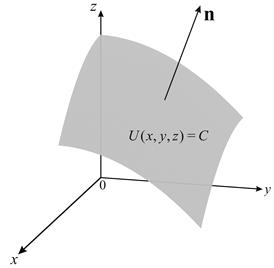
Рис. 1. К понятию градиента скалярной функции
Таким образом, градиент это вектор, который представляет собой результат применения некоего дифференциального оператора к скалярной функции.
Если векторное поле А в каждой точке М может быть задано как градиент некоторой функции U, т. е. А= grad U, то такое поле называют потенциальным, а функцию U – потенциалом.
Физический смысл градиента заключается в том, что его направление совпадает с направлением наибольшего возрастания скалярной величины. Так градиент температуры направлен к источнику тепла, а градиент потенциала электростатического поля к одиночному заряду и т.д. Модуль градиента характеризует степень возрастания скалярной величины.
|
|
Векторные поля
Если в каждой точке М области D задан определенный вектор А (М), то говорят, что в области D задано векторное поле. Примерами векторных физических полей служат гравитационное поле, электромагнитное поле, поле скоростей текущей жидкости и т.д.
Для векторного поля вводят понятие векторной линии, т.е. линии, направление касательной к которой в каждой точке совпадает с направлением вектора А (М) (Рис. 2).
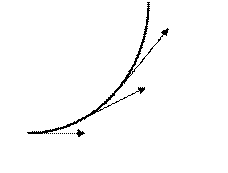 Если векторное поле определяется функцией
Если векторное поле определяется функцией
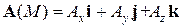 , (2)
, (2)
то векторная линия в пространстве задается следующей системой дифференциальных уравнений
|
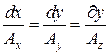 . (3)
. (3)
Поток вектора
Важным понятием для векторного поля является поток вектора. Если векторное поле задано выражением (2), то для всякой поверхности S с нормалью n можно записать интеграл по этой поверхности от проекции вектора A на нормаль n, а именно
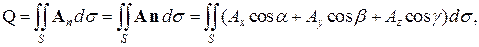 (4)
(4)
где α, β, γ – направляющие косинусы нормали. Формула (4) и определяет поток вектора A через поверхность S.
Физический смысл потока нагляднее всего иллюстрируется на примере потока жидкости, который есть не что иное, как объём жидкости, пересекающий единицу поверхности в единицу времени. Тогда поток жидкости через площадку dS будет равен объему параллелепипеда с ребром, равным скорости потока V и высотой, равной V n (см. Рис. 3), а поток жидкости через всю поверхность S будет соответственно равен
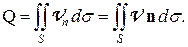 (5)
(5)
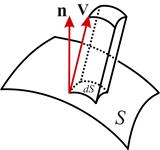
Рис. 3. К физическому смыслу потока вектора
Дивергенция вектора
Понятие потока вектора лежит в основе другого важного понятия – дивергенции вектора. Для его определения нужно рассмотреть некоторую точку векторного поля А (M) и окружить её замкнутой поверхностью S, целиком содержащейся в поле. В поле скоростей жидкости это будет соответствовать алгебраической сумме втекающей и вытекающей жидкости, которая будет равна нулю, если внутри объема отсутствуют источники и стоки жидкости.
Теперь возьмем отношение потока вектора А к объему V внутри поверхности S
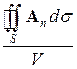 ,
,
и найдем предел этого отношения при V, стремящемся к нулю. Этот предел и называется дивергенцией или расходимостью вектора А в точке М, а именно
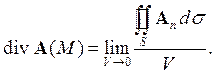 (6)
(6)
Дифференциальная форма дивергенции векторного поля, заданного формулой (2), имеет вид:
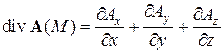 . (7)
. (7)
Таким образом, результат применения оператора дивергенции к вектору является величиной скалярной.
Пользуясь выражением для дивергенции (7), теорему Остроградского можно записать в векторном виде





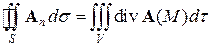 (8)
(8)
Эта форма теоремы Остроградского для поля текущей жидкости выражает тот очевидный факт, что поток жидкости через поверхность равен суммарной мощности всех источников и стоков, т.е. количеству жидкости, возникающей в рассматриваемой области в единицу времени.
|
|
Начальные условия
В случае бесконечной струны нужно сформулировать только начальные условия в следующем виде:
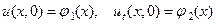 . (6)
. (6)
С физической точки зрения первое из этих условий задает смещение каждой точки струны, а второе – скорость каждой точки струны в начальный момент времени. Задача отыскания решения уравнения (4) или (5) при выполнении условий (6) называют задачей Коши.
Случай ограниченной струны.
Рассмотрим теперь струну длины l. Для ограниченной струны наряду с начальными условиями надо сформулировать и граничные условия. Существует три основных типа граничных условий.
Граничные условия I рода. В этом случае задаются перемещения на концах струны как функции времени (Рис. 7)
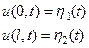 (7)
(7)
|
 . Такие условия называют однородными, а само неподвижное закрепление – защемлением.
. Такие условия называют однородными, а само неподвижное закрепление – защемлением.
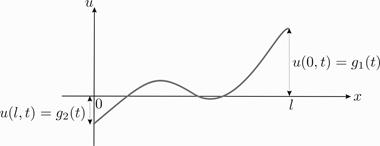
Рис. 7. Граничные условия первого рода
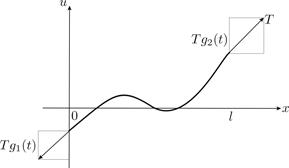
Рис. 8. Граничные условия второго рода
Граничные условия II рода. В этом случае задаются проекции силы на ось u на концах струны как функции времени. Как мы выяснили, каждая из них равна 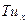 , поэтому на концах задаются производные ux как функции времени (Рис. 8)
, поэтому на концах задаются производные ux как функции времени (Рис. 8)
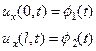 (8)
(8)
Если концы струны свободны, хотя и перемещаются только по вертикали, то в условиях (7) g 1(t) и g 2(t) будут равны нулю.
Граничные условия III рода. В этом случае лучше начать с механического смысла этих условий. Сначала предположим, что концы струны связаны с осью x (см.рис. 13), тогда со стороны каждой из пружин на концы струны по закону Гука будут действовать силы пропорциональные смещению u. Поскольку силы, действующие со стороны пружин должны быть равны вертикальным проекциям сил со стороны струны, то можно записать условия на концах следующим образом:
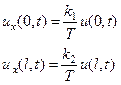 , (9)
, (9)
где k 1 и k 2 – жесткости пружин, прикрепленных к струне на концах струны. Такое граничное условие часто называют упругим закреплением струны в граничных точках
Теперь рассмотрим общий случай, когда один конец пружины прикреплен к струне, а второй движется по вертикали по заданному закону времени θ (t) (Рис. 9). Тогда условия (9) изменятся следующим образом:
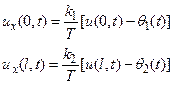 (10)
(10)
После переноса слагаемых и переобозначений мы получим граничные условия III рода в традиционном виде
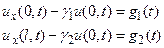 (11)
(11)
где 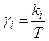 ,
, 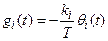 (i =1,2)
(i =1,2)
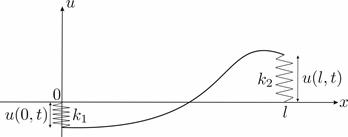
Рис. 9. Граничные условия третьего рода (частный случай).
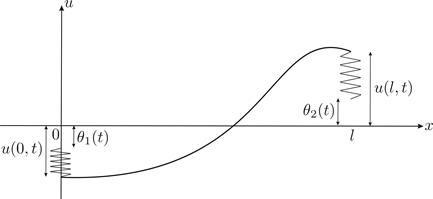
Рис. 10. Граничные условия третьего рода (общий случай).
К перечисленным видам граничных условий нужно добавить граничное условие, которое описывает действие на конце струны вертикальной силы, пропорциональной скорости и направленной в противоположном направлении. Такую силу обычно называют силой вязкого трения. Она может создаваться гидравлическим демпфером, соединяющим конец пружины с неподвижной точкой на оси x. Условие такого типа записывается (для левого конца) следующим образом:
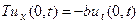 (12)
(12)
или 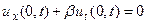 , где
, где 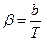 (13)
(13)
В некоторых физических задачах приходится прибегать к использованию на разных концах струны разных типов граничных условий. Например, на левом конце задается условие защемления, а на правом упругое закрепление.
Решение задачи Коши
Формула Даламбера
Чтобы выяснить, как будет вести себя бесконечная струна в отсутствии внешних сил, необходимо решить задачу Коши для уравнения (5) с начальными условиями (6), которые мы перепишем в следующем виде:
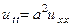 , (14)
, (14)
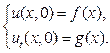 , (15)
, (15)
Одно из условий (15) может быть нулевым, но не оба, ибо в этом случае струна будет оставаться в исходном, недеформированном состоянии.
Решение задачи Коши осуществим в три этапа:
1-й шаг (приведение уравнения (7) к каноническому виду):
Введем новые переменные ξ и η следующим образом:
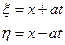 (16)
(16)
и запишем равнение (14) в новых переменных. Для этого получим выражения для uxx и utt:
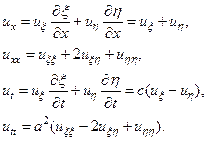
После подстановки полученных выражений в исходное уравнение (14) получим:
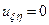 . (17)
. (17)
Уравнение (17) является каноническим видом уравнения (14), а переменные ξ и η – каноническими переменными.
2-й шаг (решение преобразованного уравнения):
Проинтегрируем полученное уравнение по ξ, а затем по η. После интегрирования по ξ, получим:
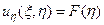 ,
,
где F (η) – произвольная функция от η.
После интегрирования по η получим
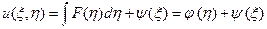 ,
,
где φ (η) и ψ (ξ) – произвольные функции своих аргументов.
3-й шаг:
Возвращаясь к старым переменным, получим

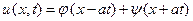 . (18)
. (18)
Физический смысл полученного решения состоит в том, что оно представляет собой суперпозицию двух волн, распространяющихся вдоль оси x в противоположных направлениях со скоростью a, как это показано на рис.11, причем формы этих волн, определяемые функциями  и ψ, являются произвольными.
и ψ, являются произвольными.
4-й шаг (Использование начальных условий):
Для конкретизации формы воспользуемся начальными условиями. Для этого подставим полученное решение и его производную по времени в начальные условия (15).
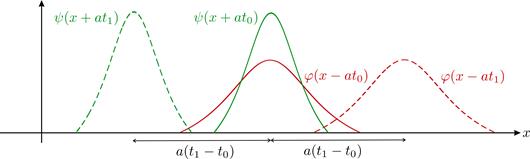
Рис. 11. Распространяющиеся волны
В результате получим два уравнения относительно неизвестных функций φ (x) и ψ (x):
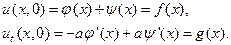
Проинтегрировав второе уравнение от x0 до x, получим систему уравнений относительно искомых функций:
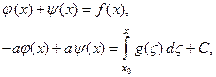
где С – произвольная константа. Решая эту систему, получим:
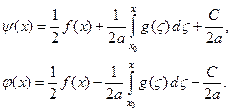
Записывая полученные решения для любого времени t, будем иметь
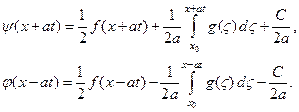
Складывая почленно оба выражения с одновременным изменением порядка интегрирования во втором из них, получим окончательный вид решения задачи Коши:
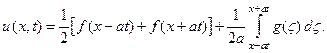 (19)
(19)
Эта формула носит название формулы Даламбера. Она была получена в предположении, что решение поставленной задачи Коши существует, а её наличие доказывает и единственность решения. Можно показать и непрерывную зависимость решения от начальных данных. В самом деле, для любого ε > 0 можно указать такое δ > 0, что если заменить f и g на f1 и g1,так, что
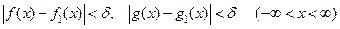 ,
,
то разность между первоначальным решением u (x, t) и новым решением u 1 (x, t) будет по абсолютной величине меньше ε на любом конечном отрезке времени, что легко следует из формулы (19).
Частные случаи
Рассмотрим два частных случая начальных условий.
1) Н а ч а л ь н ы е с к о р о с т и т о ч е к с т р у н ы р а в н ы н у л ю, а начальное смещение имеет место лишь в конечном промежутке (– b, b). В этом случае формула (19) будет иметь вид:
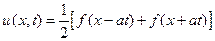 . (20)
. (20)
Решение (20) представляет собой сумму двух волн, распространяющихся влево и вправо со скоростью a, причем начальная форма обеих волн определяется функцией f (x)/2, т.е. равной половине первоначального смещения струны.
Пусть, в частности, начальное смещение неограниченной струны, материал которой таков, что 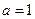 , задается следующим образом:
, задается следующим образом:
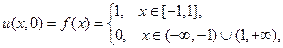
Тогда, пользуясь формулой (20), мы можем выписать выражения для смещения струны в моменты времени 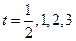 .
.
Для 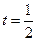 мы получим:
мы получим:
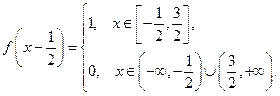
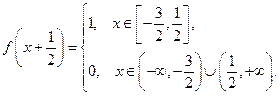
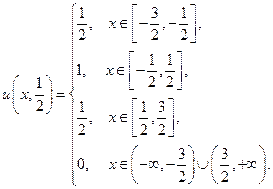
Для 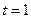 :
:
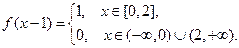
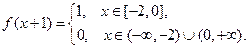
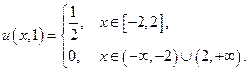
Для 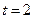 :
:
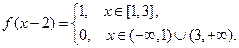
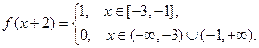
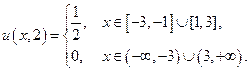
Для 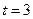 :
:
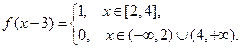
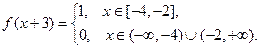
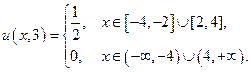
2) Н а ч а л ь н о е с м е щ е н и е р а в н о н у л ю, а функция g (x) отлична от нуля лишь в ограниченном промежутке (– b, b). В этом случае говорят, что струна имеет только начальный импульс, арешение (19) принимает вид:
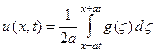 , (21)
, (21)
или полагая:
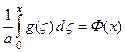 ,
,
можем записать:
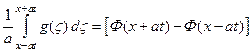 .
.
Тогда окончательно получим:
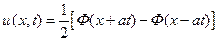 . (22)
. (22)
Отсюда видно, что и в этом случае по струне будут распространяться две волны – одна прямая и одна обратная. Результат их прохождения будет следующим. При 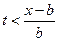 промежуток интегрирования в формуле (21) не будет иметь общих точек с интервалом (– b, b), а значит функция g (x) будет равна нулю (струна покоится). Начиная с момента времени
промежуток интегрирования в формуле (21) не будет иметь общих точек с интервалом (– b, b), а значит функция g (x) будет равна нулю (струна покоится). Начиная с момента времени 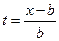 промежуток интегрирования в формуле (21) будет накладываться на интервал (– b, b) и точка x начнет смещаться. Наконец, при
промежуток интегрирования в формуле (21) будет накладываться на интервал (– b, b) и точка x начнет смещаться. Наконец, при 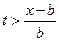 промежуток интегрирования будет целиком содержать интервал (– b, b) и интегрирование будет сводиться к интегрированию по этому интервалу, так как вне его g (x) = 0, т.е. при
промежуток интегрирования будет целиком содержать интервал (– b, b) и интегрирование будет сводиться к интегрированию по этому интервалу, так как вне его g (x) = 0, т.е. при 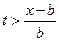 смещение u (x, t) будет иметь постоянное значение d, определяемое интегралом:
смещение u (x, t) будет иметь постоянное значение d, определяемое интегралом:
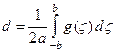 .
.
Таким образом, действие первоначального импульса приводит к тому, что с течением времени точки струны смещаются на отрезок d и остаются без движения в этом новом положении. Иначе говоря, волны оставляют после себя постоянный след своего прохождения.
Пусть, в частности, начальное смещение неограниченной струны равно нулю, а начальная скорость задается следующим образом:
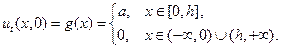
Тогда, пользуясь формулой (21) и (22), мы можем выписать выражения для смещения струны в любой момент времени.
Имея в виду, что интеграл с переменным верхним пределом от заданной функции 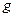 определяется выражением
определяется выражением
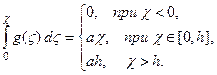
для 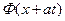 и
и 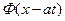 получим:
получим:
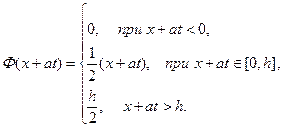
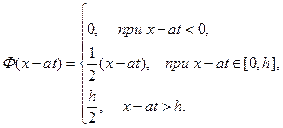
В частности, для 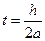 :
:
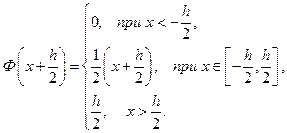
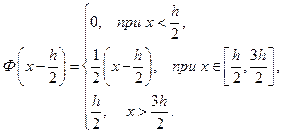
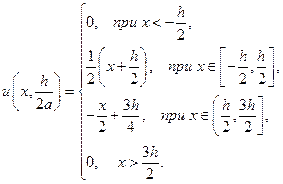
Для 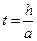 :
:
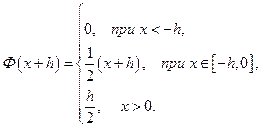
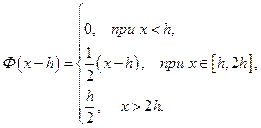
и тогда
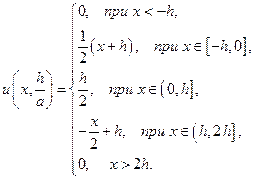
Для 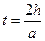 :
:
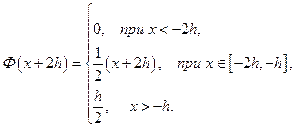
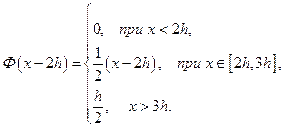
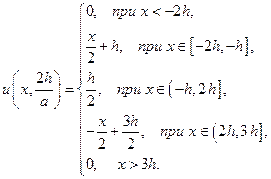
Графическая интерпретация
Первый частный случай имеет простую графическую интерпретацию. На рис. 12. показано, как начальное смещение расщепляется на две полуволны, движущиеся в противоположных направлениях.
Приведенная схема может служить графическим способом построения решения задачи Коши с нулевой начальной скоростью.
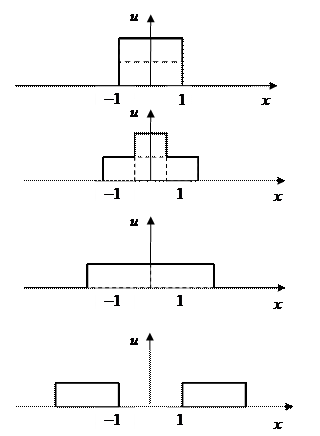
Рис. 12. Графическая иллюстрация первого частного случая.
Для второго частного случая на рис. 14 приведены графики полученного смещения в случае 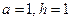 в моменты времени
в моменты времени 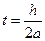 и
и 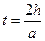
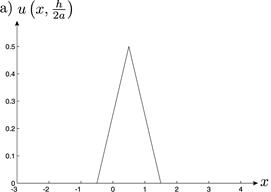
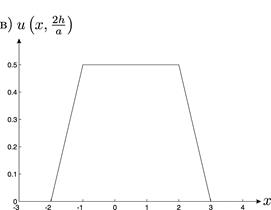
Рис. 13. Графическая иллюстрация второго частного случая.
Метод характеристик
Ещё один способ решения задачи Коши можно получить исходя из пространственно-временной интерпретации формулы Даламбера. Сначала рассмотрим 1-й частный случай, когда начальная скорость точек струны равна нулю. В этом случае решение определяется формулой (20)
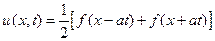
Из этой формулы следует, что функция f остается постоянной, если сохраняют свое значение выражения x – at или 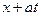 , т.е.
, т.е. 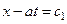 ,
, 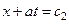 . На плоскости (x, t) эти выражения представляют собой уравнения прямых, называемых характеристиками волнового уравнения (Рис. 14).
. На плоскости (x, t) эти выражения представляют собой уравнения прямых, называемых характеристиками волнового уравнения (Рис. 14).
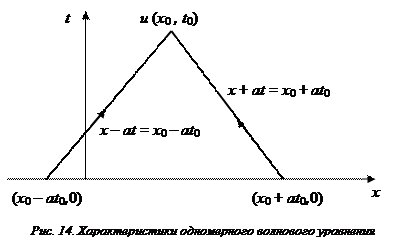
Вдоль указанных прямых функция f сохраняет своё значение, которое она имела на оси x т.е. в начальный момент времени, а совокупность этих значений нам известна как начальное смещение струны. Таким образом, решение задачи Коши для уравнения колебания струны для любой точки плоскости (x, t) можно получить, проведя через неё две характеристики, уравнения которых будут
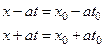
и взяв полусумму значений функции f, которые она имеет на этих характеристиках.
Используя такую интерпретацию формулы Даламбера, решим задачу, сформулированную в предыдущем параграфе, а именно
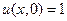 в интервале
в интервале 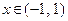 и 0 во всех остальных точках
и 0 во всех остальных точках
u t(x, 0) = 0
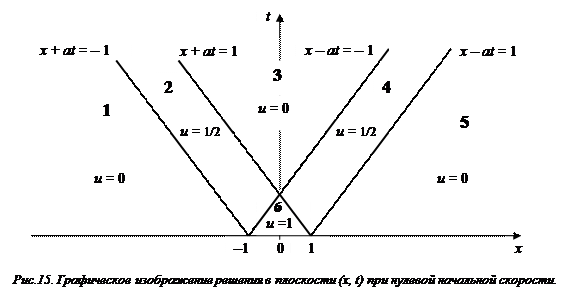
На рис. 15 решение задачи изображено в плоскости переменных x, t, а не u, x как в предыдущем параграфе. Всё полупространство получается разбитым на 6 областей. В трех из них решение равно нулю, в двух – одной второй и в одной – единице.
Теперь перейдем к случаю, когда начальное смещение равно нулю, а начальная скорость является произвольной функцией координаты g (x). В этом случае решение имеет вид (15).
Значение величины u в каждой точке(x 0, t 0) можно интерпретировать как интеграл от начальной скорости в пределах от 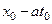 до
до 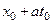 , т.е.
, т.е.
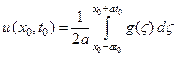 (23)
(23)
В качестве примера построим решение задачи Коши в координатах x, t с начальными условиями
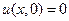
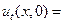
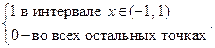
Подставляя в формулу (23) в каждой из шести областей (см. Рис.15) свои значения функции g (ζ) и свои пределы интегрирования, получим
В областях 1 и 5  и следовательно
и следовательно 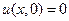 ; в остальных областях
; в остальных областях 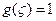 , при этом
, при этом
в области 2 пределы интегрирования от – 1 до 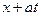 и
и 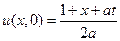 ,
,
в области 3 пределы интегрирования от + 1 до –1 и 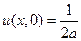 ,
,
в области 4 пределы интегрирования от 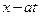 до 1 и
до 1 и 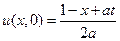 ,
,
в области 6 пределы интегрирования от 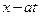 до
до 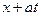 и
и 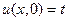 .
.
С физической точки зрения рассматриваемый процесс можно пояснить следующим образом. Пусть точка x лежит правее промежутка (– 1, 1). При t = 0 промежуток интегрирования (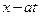 ,
, 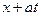 ) вырождается в точку x, а затем при увеличении t он расширяется в обе стороны со скоростью a. При
) вырождается в точку x, а затем при увеличении t он расширяется в обе стороны со скоростью a. При 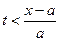 этот промежуток будет находиться вне промежутка (– 1, 1) и функция g (x) в нем будет равна нулю, а значит и u (x, t) = 0, т.е. точка x покоится. Начиная с момента времени
этот промежуток будет находиться вне промежутка (– 1, 1) и функция g (x) в нем будет равна нулю, а значит и u (x, t) = 0, т.е. точка x покоится. Начиная с момента времени 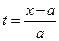 промежуток (
промежуток (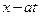 ,
, 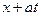 ) будет покрывать интервал (– 1, 1), в котором в котором функция g (x) равна единице и точка x начнет перемещаться по мере прохождения фронта волны через точку x. Наконец, при
) будет покрывать интервал (– 1, 1), в котором в котором функция g (x) равна единице и точка x начнет перемещаться по мере прохождения фронта волны через точку x. Наконец, при 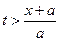 промежуток (
промежуток (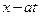 ,
, 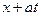 ) будет целиком содержать интервал (– 1, 1) и интегрирование будет сводиться к интегрированию в этом интервале, т.е. при
) будет целиком содержать интервал (– 1, 1) и интегрирование будет сводиться к интегрированию в этом интервале, т.е. при 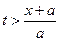 смещение токи x будет оставаться постоянным и равным 1/ a. Момент времени
смещение токи x будет оставаться постоянным и равным 1/ a. Момент времени 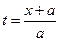 является моментом прохождения заднего фронта волны через точку x.
является моментом прохождения заднего фронта волны через точку x.
Этот процесс схематично проиллюстрирован на рис. 16. Таким образом, действие начального импульса приводит к тому, что с течением времени точки струны перемещаются на отрезок длиной u= 1/a и остаются без движения в этом новом положении. Иначе говоря, волна оставляет после себя след своего прохождения. В результате положения u= 1/a сначала достигает точка с координатой x =0, после чего область смещения постепенно распространяется на всю длину бесконечной струны.
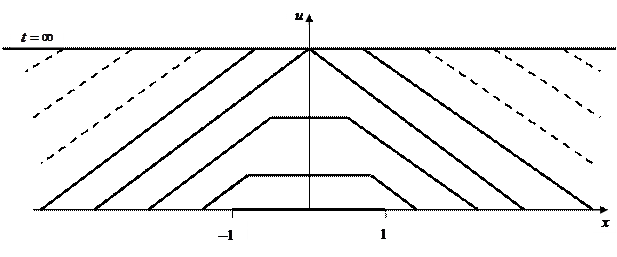
Рис. 16. Графическое изображение решения в плоскости (x, t) при нулевом начальном смещении.
Телеграфное уравнение.
Как известно, при прохождении электрического тока по проводнику, вокруг него образуется электромагнитное поле, которое в свою очередь вызывает изменения, как силы тока, так и величины напряжения. В результате в проводнике возникает определенный колебательный процесс, который мы постараемся описать уравнениями в частных производных.
Совместим ось x с осью проводника длиной l, поместив начало координат в один из его концов. Сила тока I и напряжение v в каждой точке проводника будут функциями координаты x и времени t. Выведем уравнения с частными производными, связывающие эти величины между собой. Будем предполагать, что емкость С, сопротивление R, самоиндукция L и утечка G, которая имеет место за счет несовершенства изоляции, распределены вдоль провода непрерывно, равномерно и рассчитаны на единицу длины проводника.
Применяя закон Ома к участку проводника, заключенного между двумя произвольными сечениями с координатами x 1 и x 2, мы получим
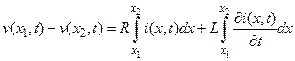 (77)
(77)
С другой стороны
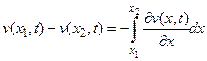 (78)
(78)
Вычитая из первого равенства второе, получим
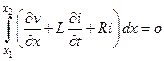
Откуда в силу произвольности интервала интегрирования следует, что
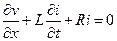 (79)
(79)
Количество электричества, протекающего через рассматриваемый участок проводника за единицу времени равно
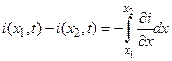
С другой стороны оно равно сумме электричества, необходимого для зарядки этого участка, и электричества, которое теряется вследствие несовершенства изоляции, т.е.
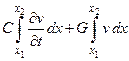
В результате сравнения этих выражений получим
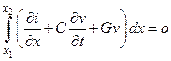 ,
,
откуда
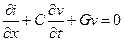 (80)
(80)
Таким образом, линейные уравнения в частных производных первого порядка (79) и (80) описывают свободные электрические колебания в проводнике.
Если мы теперь продифференцируем уравнение (79) по x, а уравнение (80) по t, а затем исключим из полученных уравнений смешанную производную 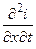 , то получим следующее линейное дифференциальное уравнение второго порядка относительно v:
, то получим следующее линейное дифференциальное уравнение второго порядка относительно v:
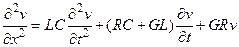 (81)
(81)
Аналогичным образом получим дифференциальное уравнение относительно i:
 (82)
(82)
В результате получим, что напряжение v и сила тока i удовлетворяют одному и тому же дифференциальному уравнению:
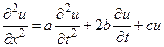 , (83)
, (83)
где 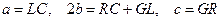 .
.
Это уравнение называют телеграфным уравнением. Нетрудно заметить, что при 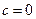 оно по форме совпадает с уравнением колебания струны (или стержня) с учетом процесса затухания.
оно по форме совпадает с уравнением колебания струны (или стержня) с учетом процесса затухания.
Задача Гурса
В этом параграфе мы коротко познакомимся с задачей определения решения уравнен
|
|
|
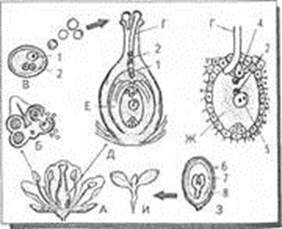
Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
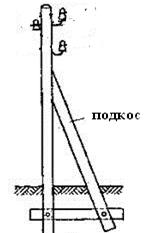
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!