Рассмотрим задачу о колебаниях ограниченной струны длины l с нулевыми граничными условиями первого рода и произвольными начальными условиями в отсутствии внешней силы. Такие колебания струны называются свободными. Решение этой задачи сводится к решению волнового уравнения
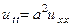 (30)
(30)
при граничных условиях  (31)
(31)
и начальных условиях 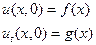 (32)
(32)
при этом искомое решение должно быть нетривиальным и ограниченным.
В этом случае можно было бы решать задачу по формуле Даламбера
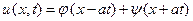
Однако определение функций  и
и  по формулам, которые мы получили из начальных условий
по формулам, которые мы получили из начальных условий
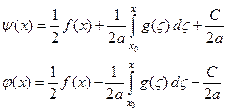 ,
,
встречает здесь те же затруднения, что и в случае полубесконечной струны, поскольку функции f (x) и g (x) определены только для x > 0 и решение может быть определено тоже только при x > 0.
В связи с этим приходится искать продолжение функций f (x) и g (x) вне промежутка (0, l), используя для этого граничные условия. Этот путь приводит, как мы помним, к построению отраженных волн и формированию решения в виде суперпозиции прямой и обратной волны. Поскольку струна закреплена с обоих концов, то прямая и обратная волны будут пересекаться многократно, что мешает наглядно представить этот процесс.
Ситуация упростилась бы, если бы можно было посмотреть как формируется решение отдельно по координате и по времени. Этот подход можно реализовать с помощью методом разделения переменных, который является одним из наиболее распространенных методов математической физики, в чем мы ещё не раз убедимся. В соответствии с этим методом решение уравнения в частных производных ищется в виде произведения функций, каждая из которых зависит только от одной переменной. В частности для уравнения (30) решение ищется в виде
 (33)
(33)
Подставив это выражение в уравнение (30), получим
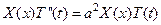
Разделим обе части на 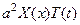 , тогда уравнение примет вид
, тогда уравнение примет вид
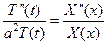
В этом уравнении левая часть есть функция только переменной t, а правая – только переменной x. Это может иметь место, только если и левая и правая часть является постоянной величиной, которую мы обозначим λ:

 (34)
(34)
где λ, может быть любым действительным числом и знак минус с этой точки зрения ничего не меняет, но для дальнейшего такое обозначения константы разделения оказывается более удобным. Заметим, что значение λ еще предстоит найти и только в том случае если оно существует наше представление (33) оправданно. В связи с этим существование значения (или значений) числа λ называют условием разделения переменных.
Соотношение (33) позволяет нам записать два уравнения:
 (35)
(35)
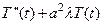 (36)
(36)
Чтобы функция (33), отличная от тождественного нуля, удовлетворяла нулевым граничным условиям (31), приходится потребовать, чтобы выполнялись условия
 и
и  (37)
(37)
Таким образом, мы приходим к необходимости решить две задачи. Первая из них состоит в том, что требуется найти нетривиальное и ограниченное при всех x решение уравнения (35), удовлетворяющее граничным условиям (37), а также те значения λ, при которых это решение существует. Эта двоякая задача носит название задачи Штурма-Лиувилля. Найденные в результате решения задачи значения λ называются собственными числами, а соответствующие им решения X (x) – собственными функциями.
Уравнение (35), как известно, имеет три вида решения в зависимости от того, какие корни имеет соответствующее характеристическое уравнение
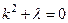

В результате при λ = 0 учет нулевых граничных условий приводит к тривиальному решению, что противоречит условию задачи. При λ < 0 решение имеет вид

Подстановка первого граничного условия приводит к равенству  , а подстановка второго граничного условия приводит к равенству
, а подстановка второго граничного условия приводит к равенству  , чего не может быть, если
, чего не может быть, если  . Остается только случай λ > 0, тогда решение будет иметь вид
. Остается только случай λ > 0, тогда решение будет иметь вид
 ,
,
В котором в силу первого граничного условия С 1 = 0, а второе граничное условие приводит к соотношению
 ,
,
откуда получаем  , где n= 1, 2, 3,...,
, где n= 1, 2, 3,...,  .
.
В результате получаем бесконечный набор собственных чисел, каждому из которых соответствует собственная функция
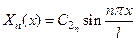 , (38)
, (38)
где 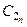 – произвольные постоянные. Эта функция представляет собой с точностью до множителя синус кратного аргумента
– произвольные постоянные. Эта функция представляет собой с точностью до множителя синус кратного аргумента
Теперь можно обратиться к решению уравнения (36). Поскольку мы имеем бесконечный набор значений λ, то вместо уравнения (36) нам предстоит решать бесконечный набор уравнений одного вида
 , где
, где  (39)
(39)
При этих значения λ уравнение (36) будет иметь решение
 , (40)
, (40)
где An и Bn – произвольные постоянные, свои для каждого n.
В результате, перебирая значения n. мы получим бесконечный набор решений уравнения (33) следующего вида:
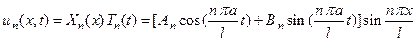 (41)
(41)
При записи выражения (41) было учтено, что произведение произвольной константы C2n на произвольные константы An и Bn будет также давать произвольные константы, которые можно снова обозначить через An и Bn.
Сумма решений (41) и будет общим решением уравнения (33)
 (42)
(42)
Каждая из функций un (x) представляет собой так называемую стоячую волну. Действительно, как мы уже отмечали, множитель sin(nπx/l) представляет собой периодическую функцию по координате x с полупериодом, равным 1/n от длины струны, а множитель в квадратных скобках представляет собой периодическую по времени функцию
 , (43)
, (43)
где Dn2= An2+Bn2 и γ n=arctg (An /Bn), с периодом, пропорциональным 1/ n. Амплитуда колебания каждой точки с координатой x определяется по формуле
 , (44)
, (44)
а частота по формуле
 (45)
(45)
Стоячую волну с номером n называют n-ой гармоникой или n-ой модой колебаний.
На рис.18 приведены примеры графического изображения стоячих волн для n= 1,2,3. Константы An и Bn, а значит и константа Dn, представляющая собой амплитуду колебаний, остается пока неизвестной.

Рис. 18. Стоячие волны: а) n=1; б) n=2; в) n=3.
Теперь перейдем к определению констант An и Bn. Для этого воспользуемся начальными условиями (32), подставив полученное решение (42) с учетом (43). В результате получим
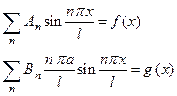 (46)
(46)
Умножим обе части на 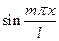 , проинтегрируем от нуля до l и воспользуемся соотношением ортогональности
, проинтегрируем от нуля до l и воспользуемся соотношением ортогональности
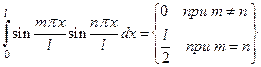 ,
,
после чего получим 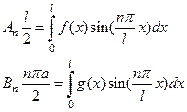
Окончательные выражения для коэффициентов An и Bn будут иметь вид
 (47)
(47)
Таким образом, решение задачи о малых поперечных свободных колебаниях ограниченной струны, защемленных на обоих концах, имеет вид суперпозиции бесконечного набора стоячих волн, которые определяются по формуле (41) с учетом формул (47).



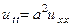 (30)
(30) (31)
(31)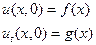 (32)
(32)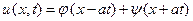
 и
и  по формулам, которые мы получили из начальных условий
по формулам, которые мы получили из начальных условий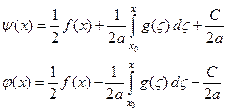 ,
, (33)
(33)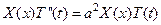
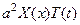 , тогда уравнение примет вид
, тогда уравнение примет вид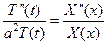

 (34)
(34) (35)
(35)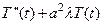 (36)
(36) и
и  (37)
(37)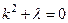

 , а подстановка второго граничного условия приводит к равенству
, а подстановка второго граничного условия приводит к равенству  , чего не может быть, если
, чего не может быть, если  . Остается только случай λ > 0, тогда решение будет иметь вид
. Остается только случай λ > 0, тогда решение будет иметь вид ,
, ,
, , где n= 1, 2, 3,...,
, где n= 1, 2, 3,...,  .
.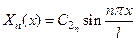 , (38)
, (38)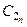 – произвольные постоянные. Эта функция представляет собой с точностью до множителя синус кратного аргумента
– произвольные постоянные. Эта функция представляет собой с точностью до множителя синус кратного аргумента , где
, где  , (40)
, (40)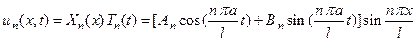 (41)
(41) (42)
(42) , (43)
, (43) , (44)
, (44) (45)
(45)
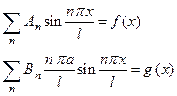 (46)
(46)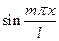 , проинтегрируем от нуля до l и воспользуемся соотношением ортогональности
, проинтегрируем от нуля до l и воспользуемся соотношением ортогональности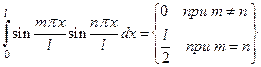 ,
,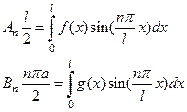
 (47)
(47)


