Формулировка большинства традиционных задач физики приводит к линейным уравнениям в частных производных второго порядка с постоянными коэффициентами.
Так, при изучении различных видов волн, а также других колебательных явлений мы приходим к так называемому волновому уравнению
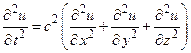 (3)
(3)
Процессы распространения тепла в однородном теле, так же как и явления диффузии описываются уравнением теплопроводности
 (4)
(4)
При рассмотрении установившегося теплового состояния, электрического поля или поля тяготения мы приходим к уравнению Пуассона
 (5)
(5)
При отсутствии источников тепла, электрических зарядов или масс уравнение (5) переходит к уравнению Лапласа
 (6)
(6)
Уравнения (3)–(6) являются линейными уравнениями второго порядка с постоянными коэффициентами. Их часто называют основными уравнениями математической физики.
Следует также привести уравнение, которым приходится пользоваться при описании некоторых волновых процессов и которое называется телеграфным уравнением
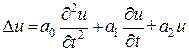 , (7)
, (7)
где  . Это уравнение при
. Это уравнение при 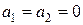 переходит в волновое уравнение (3), при
переходит в волновое уравнение (3), при 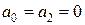 в уравнение теплопроводности и диффузии (4), а при
в уравнение теплопроводности и диффузии (4), а при  в уравнение диффузии с химическими реакциями.
в уравнение диффузии с химическими реакциями.
Каждое из уравнений (3) – (7) принадлежит к одному из трех типов. Тип уравнения определяется в некоторой фиксированной точке М0 (x0 , y0 , z0 , t0). Определение типа уравнения удобнее всего сформулировать для квазилинейного уравнения второго порядка, записанного в следующем виде:
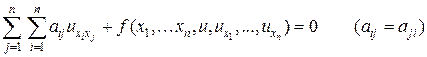 (8)
(8)
где aij, и bi – функции x1,…xn. При x= 4 в качестве x1,x2,x3 могут выступать пространственные координаты x,y,z, а в качестве x4 – время t. Составив затем в фиксированной точке  квадратичную форму
квадратичную форму
 (9)
(9)
Уравнение (7) в точке М0 принадлежит к элептическому типу, если в этой точке квадратичная форма (8) является положительно или отрицательно определенной.
Уравнение (7) в точке М0 принадлежит к гиперболическому типу, если в этой точке квадратичная форма (8) при приведении её к сумме квадратов имеет все коэффициенты, кроме одного, одного, определенного знака, а оставшийся один коэффициент противоположного знака.
Уравнение (7) в точке М0 принадлежит к параболичекому типу, если в этой точке квадратичная форма (8) при приведении её к сумме квадратов имеет только один коэффициент, равный нулю, а все другие коэффициенты имеют одинаковые знаки.
Посколькукоэффициенты aij, и bi являются функциями x1,…xn, то при переходе от одной точки к другой уравнение (7) может менять свою принадлежность к тому или иному типу. В связи с этим, уравнение принадлежит к тому или иному типу в некоторой области D, если оно принадлежит к этому типу в каждой точке этой области.
Для квазилинейного уравнения второго порядка с двумя независимыми переменными тип уравнения определяется более наглядно. Для этого его нужно записать в следующем виде:
 (10)
(10)
где коэффициенты A,B и C есть функции x и y.
Уравнение (9) принадлежит
а) к гиперболическому типу, если  ;
;
б) к параболическому типу, если  ;
;
в) к эллиптическому типу, если 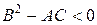 .
.
В записанных выше уравнениях (3) – (6) коэффициенты при производных являются постоянными, поэтому при переходе от одной точки к другой тип уравнения сохраняется. В связи с этим во всей области решения задачи уравнение (3) является уравнением гиперболического типа, уравнение (4) – уравнением параболического типа, а уравнения (5) и (6) уравнениями элептического типа.
Г л а в а I. Скалярные и векторные поля. Дифференциальные операторы
Скалярные поля
Цель этой короткой главы – лишь напомнить некоторые понятия, результаты, их математические формулировки и физический смысл, которые излагаются в курсе математического анализа, и которые потребуются нам в дальнейшем при изложении материала. Это касается понятий скалярного и векторного полей, а также дифференциальных операторов, применяемых к этим полям.
Наряду с понятием скалярной и векторной физической величины в математической физике часто пользуются понятиями скалярного поля и векторного поля.
Если в каждой точке М области D задано значение скалярной величины u, то эта величина является скалярной функцией точки, т.е. 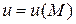 . В этом случае говорят, что в области D задано скалярное поле.
. В этом случае говорят, что в области D задано скалярное поле.
Для скалярного поля вводится понятие поверхности уровня, которая определяется как геометрическое место точек, в которых функция u имеет постоянное значение. В трехмерном случае это можно записать как
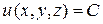 .
.
Градиент скалярной величины
Наряду с понятием поверхности уровня вводится понятие градиента, т.е. векторной величины, направление которой совпадает с направлением нормали к поверхности уровня скалярного поля (Рис. 1). Проекциями этого вектора на координатные оси служат частные производные от функции 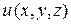

 , т. е.:
, т. е.:
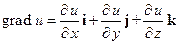 . (1)
. (1)
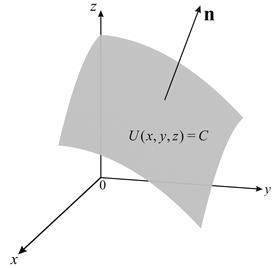
Рис. 1. К понятию градиента скалярной функции
Таким образом, градиент это вектор, который представляет собой результат применения некоего дифференциального оператора к скалярной функции.
Если векторное поле А в каждой точке М может быть задано как градиент некоторой функции U, т. е. А= grad U, то такое поле называют потенциальным, а функцию U – потенциалом.
Физический смысл градиента заключается в том, что его направление совпадает с направлением наибольшего возрастания скалярной величины. Так градиент температуры направлен к источнику тепла, а градиент потенциала электростатического поля к одиночному заряду и т.д. Модуль градиента характеризует степень возрастания скалярной величины.
Векторные поля
Если в каждой точке М области D задан определенный вектор А (М), то говорят, что в области D задано векторное поле. Примерами векторных физических полей служат гравитационное поле, электромагнитное поле, поле скоростей текущей жидкости и т.д.
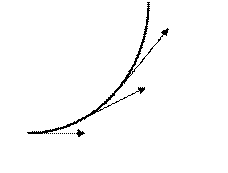
Для векторного поля вводят понятие векторной линии, т.е. линии, направление касательной к которой в каждой точке совпадает с направлением вектора А (М) (Рис. 2).
 Если векторное поле определяется функцией
Если векторное поле определяется функцией
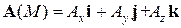 , (2)
, (2)
то векторная линия в пространстве задается следующей системой дифференциальных уравнений
| Рис. 2. К понятию векторной линии
| |
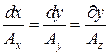
. (3)
Поток вектора
Важным понятием для векторного поля является поток вектора. Если векторное поле задано выражением (2), то для всякой поверхности S с нормалью n можно записать интеграл по этой поверхности от проекции вектора A на нормаль n, а именно
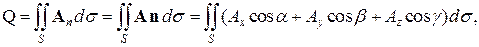 (4)
(4)
где α, β, γ – направляющие косинусы нормали. Формула (4) и определяет поток вектора A через поверхность S.
Физический смысл потока нагляднее всего иллюстрируется на примере потока жидкости, который есть не что иное, как объём жидкости, пересекающий единицу поверхности в единицу времени. Тогда поток жидкости через площадку dS будет равен объему параллелепипеда с ребром, равным скорости потока V и высотой, равной V n (см. Рис. 3), а поток жидкости через всю поверхность S будет соответственно равен
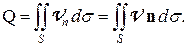 (5)
(5)
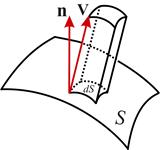
Рис. 3. К физическому смыслу потока вектора
Дивергенция вектора
Понятие потока вектора лежит в основе другого важного понятия – дивергенции вектора. Для его определения нужно рассмотреть некоторую точку векторного поля А (M) и окружить её замкнутой поверхностью S, целиком содержащейся в поле. В поле скоростей жидкости это будет соответствовать алгебраической сумме втекающей и вытекающей жидкости, которая будет равна нулю, если внутри объема отсутствуют источники и стоки жидкости.
Теперь возьмем отношение потока вектора А к объему V внутри поверхности S
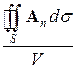 ,
,
и найдем предел этого отношения при V, стремящемся к нулю. Этот предел и называется дивергенцией или расходимостью вектора А в точке М, а именно
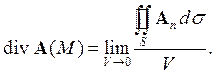 (6)
(6)
Дифференциальная форма дивергенции векторного поля, заданного формулой (2), имеет вид:
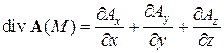 . (7)
. (7)
Таким образом, результат применения оператора дивергенции к вектору является величиной скалярной.
Пользуясь выражением для дивергенции (7), теорему Остроградского можно записать в векторном виде





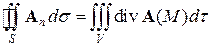 (8)
(8)
Эта форма теоремы Остроградского для поля текущей жидкости выражает тот очевидный факт, что поток жидкости через поверхность равен суммарной мощности всех источников и стоков, т.е. количеству жидкости, возникающей в рассматриваемой области в единицу времени.



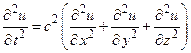 (3)
(3) (4)
(4) (5)
(5) (6)
(6)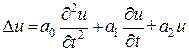 , (7)
, (7) . Это уравнение при
. Это уравнение при 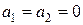 переходит в волновое уравнение (3), при
переходит в волновое уравнение (3), при 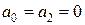 в уравнение теплопроводности и диффузии (4), а при
в уравнение теплопроводности и диффузии (4), а при  в уравнение диффузии с химическими реакциями.
в уравнение диффузии с химическими реакциями.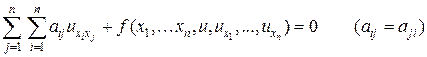 (8)
(8) квадратичную форму
квадратичную форму (9)
(9) (10)
(10) ;
; ;
;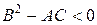 .
.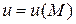 . В этом случае говорят, что в области D задано скалярное поле.
. В этом случае говорят, что в области D задано скалярное поле.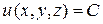 .
.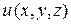

 , т. е.:
, т. е.: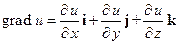 . (1)
. (1)
 Если векторное поле определяется функцией
Если векторное поле определяется функцией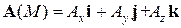 , (2)
, (2)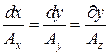 . (3)
. (3)
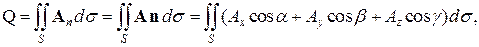 (4)
(4)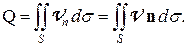 (5)
(5)
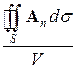 ,
,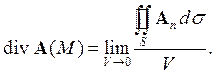 (6)
(6)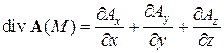 . (7)
. (7)
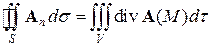 (8)
(8)

