Пусть в трехмерном пространстве с прямоугольной системой координат  задана замкнутая область (тело)
задана замкнутая область (тело)  , ограниченная поверхностью
, ограниченная поверхностью  . Рассмотрим в
. Рассмотрим в  функцию
функцию  (или
(или  , где
, где 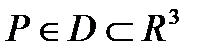 ). Разобьем тело
). Разобьем тело  произвольным образом на
произвольным образом на  областей
областей 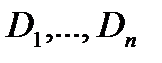 , которые могут пересекаться только по своим границам.
, которые могут пересекаться только по своим границам.
Обозначим объем тела  через
через  . Тогда
. Тогда
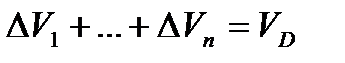 , где
, где  - объем тела
- объем тела  .
.
В каждой из областей  выберем произвольным образом точку
выберем произвольным образом точку  и вычислим значение
и вычислим значение  функции
функции  в выбранной точке.
в выбранной точке.
О п р е д е л е н и е 1. Сумма вида
 (1)
(1)
называется тройной интегральной суммой для функции  в области
в области 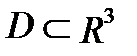 . Число
. Число  называется диаметром разбиения области
называется диаметром разбиения области  .
.
О п р е д е л е н и е 2. Если существует конечный предел тройной интегральной суммы (1) при стремлении диаметра разбиения к нулю и этот предел не зависит ни от способа разбиения области  на части, ни от выбора в них промежуточных точек, то он называется тройным интегралом от функции
на части, ни от выбора в них промежуточных точек, то он называется тройным интегралом от функции  по области
по области 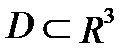 , а функция
, а функция  называется интегрируемой в
называется интегрируемой в  .
.
Для тройного интеграла используется обозначение: 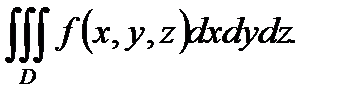 Следовательно, по определению имеем:
Следовательно, по определению имеем:
 . (2)
. (2)
З а м е ч а н и е 1. Тройной интеграл (2) существует, если функция  непрерывна в
непрерывна в  . Поэтому всюду далее, говоря об интегрируемости функции
. Поэтому всюду далее, говоря об интегрируемости функции 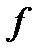 в области
в области 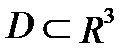 , будем предполагать ее непрерывность в
, будем предполагать ее непрерывность в  .
.
СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА
С в о й с т в о 1. Пусть функция  интегрируема в области
интегрируема в области 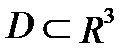 и
и  , где
, где  пересекаются только по своим границам. Тогда функция
пересекаются только по своим границам. Тогда функция  интегрируема отдельно на
интегрируема отдельно на  и на
и на  , причем справедливо равенство:
, причем справедливо равенство:

С в о й с т в о 2. Если функции  и
и  интегрируемы в области
интегрируемы в области 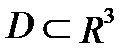 , то в
, то в  интегрируемы следующие функции:
интегрируемы следующие функции:
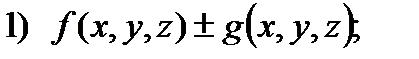
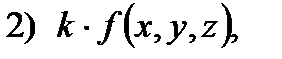 где
где 


 если
если 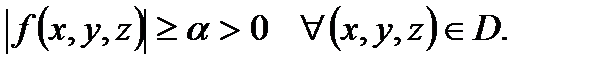
При этом для функций 1) – 3) справедливы формулы:

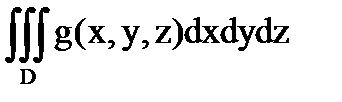 ,
,
 ,
,  .
.
С в о й с т в о 3. Если функции 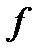 и
и  интегрируемы в области
интегрируемы в области  и
и  то выполняется неравенство:
то выполняется неравенство:
 .
.
С в о й с т в о 4. Если функция 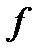 интегрируема в области
интегрируема в области  и
и  то выполняется неравенство:
то выполняется неравенство:
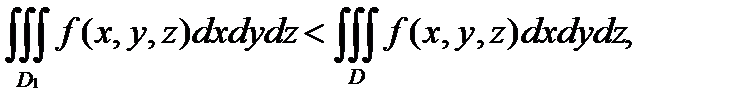 если
если  .
.
С в о й с т в о 5 (теорема о среднем значении). Если функция  непрерывна в области
непрерывна в области 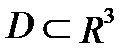 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка  , в которой выполняется равенство:
, в которой выполняется равенство:
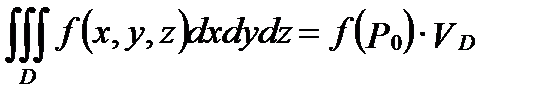 , где
, где  - объем тела
- объем тела 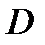 .
.
С в о й с т в о 6. Справедливо равенство:
 , где
, где  - объем области
- объем области  . (3)
. (3)
С в о й с т в о 7. Справедливо равенство:
 , (4)
, (4)
где  - масса тела
- масса тела 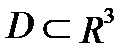 , если
, если 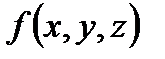 - плотность распределения массы внутри тела
- плотность распределения массы внутри тела 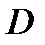 .
.
С в о й с т в о 8. Если  – плотность распределения массы внутри тела
– плотность распределения массы внутри тела  , то координаты
, то координаты  центра тяжести тела
центра тяжести тела 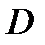 вычисляются по формулам:
вычисляются по формулам:

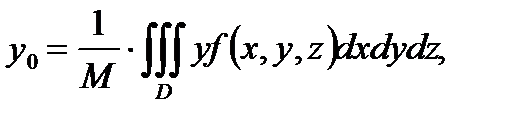
 , (5)
, (5)
где  - масса тела
- масса тела 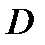 .
.
З а м е ч а н и е 2. Для однородного тела (когда 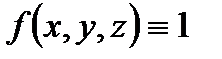 , где
, где 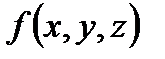 - плотность распределения массы внутри тела
- плотность распределения массы внутри тела 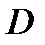 ) координаты
) координаты  центра тяжеститела
центра тяжеститела 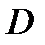 вычисляются по формулам:
вычисляются по формулам:

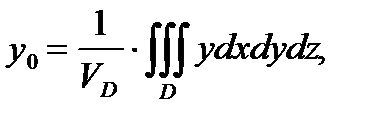
 , (6)
, (6)
где  - объем тела
- объем тела 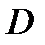 .
.
ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
Для вычисления тройного интеграла от функции  по области
по области 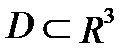 проецируем
проецируем 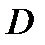 на плоскость
на плоскость 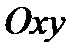 . Обозначим полученную проекцию
. Обозначим полученную проекцию  .
.
Предположим, что область 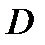 обладает следующим свойством: всякая прямая, параллельная
обладает следующим свойством: всякая прямая, параллельная 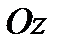 и проходящая через внутреннюю точку области
и проходящая через внутреннюю точку области 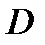 , пересекает поверхность
, пересекает поверхность  , ограничивающую область
, ограничивающую область 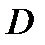 , только в двух точках.
, только в двух точках.
Пусть  и
и 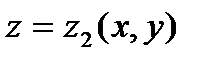 – уравнения поверхностей, ограничивающих область
– уравнения поверхностей, ограничивающих область 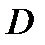 , соответственно, снизу и сверху (рис. 1).
, соответственно, снизу и сверху (рис. 1).
z
z2 (x,y)
D
z 1 (x, y)
O у
(x; y) 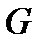
Х Рис. 1
Т е о р е м а 1. Пусть область  определяется неравенствами:
определяется неравенствами:  . Пусть функция
. Пусть функция  непрерывна в
непрерывна в  ; функции
; функции 
 непрерывны в
непрерывны в  ; функции
; функции  непрерывны на
непрерывны на  . Тогда справедливо равенство:
. Тогда справедливо равенство:
 . (7)
. (7)
П р и м е р 1. Вычислить объем тела  , ограниченного параболоидом
, ограниченного параболоидом  и плоскостью
и плоскостью  .
.
Р е ш е н и е. Тело  изображено на рис. 2.
изображено на рис. 2.
z
4
O 2 y
x Рис. 2
Объем тела 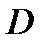 вычисляется по формуле:
вычисляется по формуле:
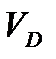 =
=  .
.
Тело 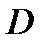 определяется неравенствами
определяется неравенствами  . Поэтому проекцией тела
. Поэтому проекцией тела 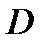 на плоскость Оху является круг
на плоскость Оху является круг 
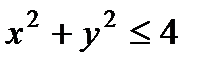 .
.
Для вычисления тройного интеграла  перейдем к цилиндрическим координатам:
перейдем к цилиндрическим координатам:  . Тогда
. Тогда


Следовательно, получаем:

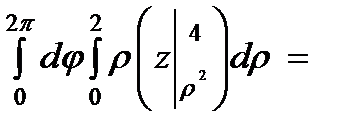
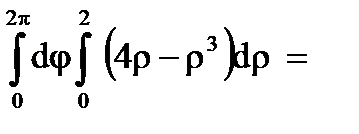
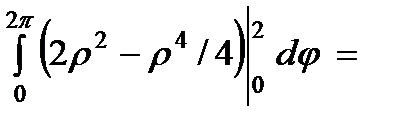
 .
.
О т в е т:  .
.
П р и м е р 2. Вычислить тройной интеграл 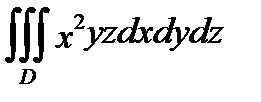 , если область
, если область 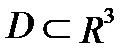 ограничена плоскостями:
ограничена плоскостями:
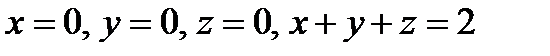 .
.
Р е ш е н и е. Нетрудно видеть, что область  ограничена снизу – плоскостью
ограничена снизу – плоскостью 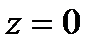 , сверху - плоскостью
, сверху - плоскостью  . В данном случае область
. В данном случае область 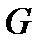 (то есть проекция тела
(то есть проекция тела  на плоскость
на плоскость  ) - область, ограниченная прямыми
) - область, ограниченная прямыми  (рис. 3).
(рис. 3).
y
x =0 y =2- x
G
О y =0 2 x
Рис. 3
Следовательно, область  определяется неравенствами:
определяется неравенствами:
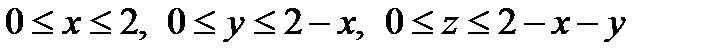 .
.
Кроме того, все участвующие в примере функции, непрерывны. Поэтому, применив формулу (7), последовательно получаем:





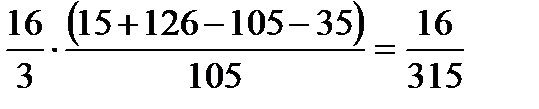 .
.
О т в е т: 



 задана замкнутая область (тело)
задана замкнутая область (тело)  , ограниченная поверхностью
, ограниченная поверхностью  . Рассмотрим в
. Рассмотрим в  (или
(или  , где
, где 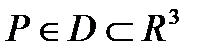 ). Разобьем тело
). Разобьем тело  произвольным образом на
произвольным образом на  областей
областей 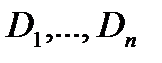 , которые могут пересекаться только по своим границам.
, которые могут пересекаться только по своим границам. через
через  . Тогда
. Тогда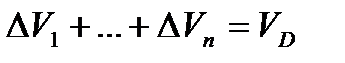 , где
, где  - объем тела
- объем тела  .
. выберем произвольным образом точку
выберем произвольным образом точку  и вычислим значение
и вычислим значение  функции
функции  в выбранной точке.
в выбранной точке. (1)
(1) в области
в области 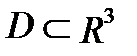 . Число
. Число  называется диаметром разбиения области
называется диаметром разбиения области  по области
по области 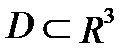 , а функция
, а функция  называется интегрируемой в
называется интегрируемой в 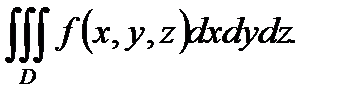 Следовательно, по определению имеем:
Следовательно, по определению имеем: . (2)
. (2) непрерывна в
непрерывна в  . Поэтому всюду далее, говоря об интегрируемости функции
. Поэтому всюду далее, говоря об интегрируемости функции 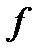 в области
в области  интегрируема в области
интегрируема в области  , где
, где  пересекаются только по своим границам. Тогда функция
пересекаются только по своим границам. Тогда функция  интегрируема отдельно на
интегрируема отдельно на  и на
и на  , причем справедливо равенство:
, причем справедливо равенство:
 интегрируемы в области
интегрируемы в области  интегрируемы следующие функции:
интегрируемы следующие функции: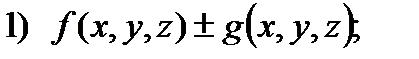
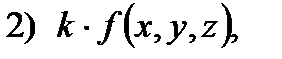 где
где 


 если
если 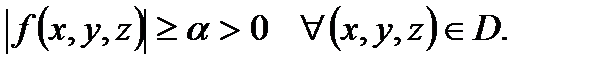

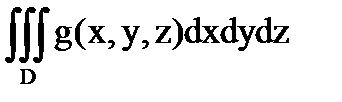 ,
, ,
,  .
. интегрируемы в области
интегрируемы в области  и
и  то выполняется неравенство:
то выполняется неравенство: .
. то выполняется неравенство:
то выполняется неравенство: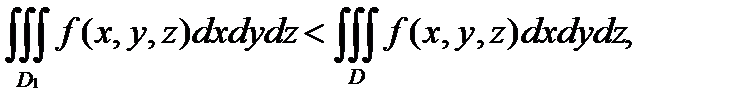 если
если  .
. , в которой выполняется равенство:
, в которой выполняется равенство: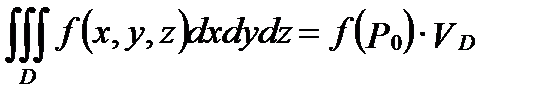 , где
, где  - объем тела
- объем тела 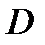 .
. , где
, где  . (3)
. (3) , (4)
, (4) - масса тела
- масса тела 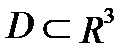 , если
, если 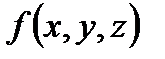 - плотность распределения массы внутри тела
- плотность распределения массы внутри тела 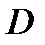 .
. – плотность распределения массы внутри тела
– плотность распределения массы внутри тела  , то координаты
, то координаты  центра тяжести тела
центра тяжести тела 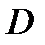 вычисляются по формулам:
вычисляются по формулам:
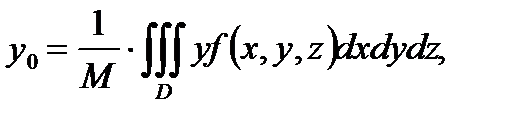
 , (5)
, (5) - масса тела
- масса тела 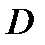 .
.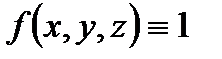 , где
, где 
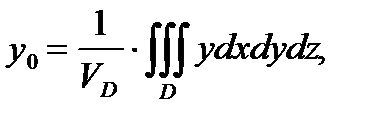
 , (6)
, (6)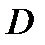 на плоскость
на плоскость 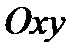 . Обозначим полученную проекцию
. Обозначим полученную проекцию  .
.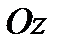 и проходящая через внутреннюю точку области
и проходящая через внутреннюю точку области 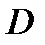 , пересекает поверхность
, пересекает поверхность  , ограничивающую область
, ограничивающую область  и
и 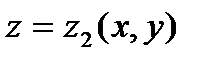 – уравнения поверхностей, ограничивающих область
– уравнения поверхностей, ограничивающих область 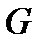
 . Пусть функция
. Пусть функция  непрерывна в
непрерывна в  ; функции
; функции 
 непрерывны в
непрерывны в  ; функции
; функции  непрерывны на
непрерывны на  . Тогда справедливо равенство:
. Тогда справедливо равенство: . (7)
. (7) и плоскостью
и плоскостью  .
.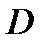 вычисляется по формуле:
вычисляется по формуле: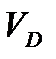 =
=  .
. . Поэтому проекцией тела
. Поэтому проекцией тела 
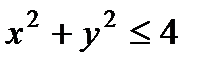 .
. . Тогда
. Тогда


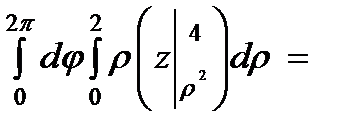
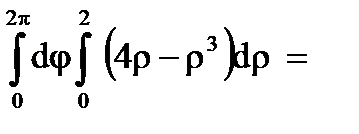
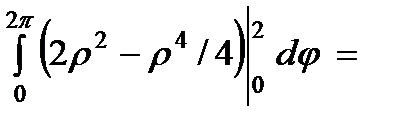
 .
. .
.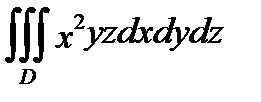 , если область
, если область 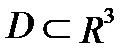 ограничена плоскостями:
ограничена плоскостями: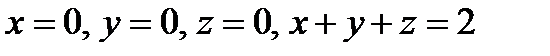 .
. ограничена снизу – плоскостью
ограничена снизу – плоскостью 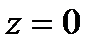 , сверху - плоскостью
, сверху - плоскостью  . В данном случае область
. В данном случае область 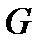 (то есть проекция тела
(то есть проекция тела  ) - область, ограниченная прямыми
) - область, ограниченная прямыми  (рис. 3).
(рис. 3).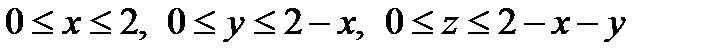 .
.




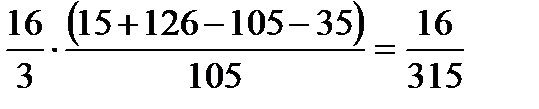 .
.



