Рассмотрим функцию  дифференцируемую в точке
дифференцируемую в точке 
О п р е д е л е н и е 3. Дифференциалом второго порядка  функции
функции  в точке
в точке  называется полный дифференциал от ее дифференциала первого порядка, вычисленный в точке
называется полный дифференциал от ее дифференциала первого порядка, вычисленный в точке  :
: 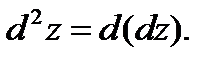
Аналогично вводится дифференциал n-го порядка функции  обозначаемый
обозначаемый  Это – полный дифференциал от ее дифференциала (n -1)-го порядка, то есть
Это – полный дифференциал от ее дифференциала (n -1)-го порядка, то есть

В случае функции двух переменных  справедливы равенства:
справедливы равенства:
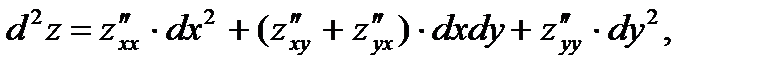 (1)
(1)
если  независимые переменные;
независимые переменные;

 (2)
(2)
если  функции одной или нескольких переменных.
функции одной или нескольких переменных.
З а м е ч а н и е 2. Сравнение формул (1) и (2) приводит к выводу: уже второй дифференциал не обладает свойством инвариантности его формы.
З а м е ч а н и е 3. В формулах(1) и (2) следует различать выражения:  и
и  дифференциал второго порядка функции
дифференциал второго порядка функции 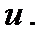
При решении многих задач полезно знание следующего утверждения.
Т е о р е м а 2 (аналитический признак полного дифференциала).Пусть функции  определены в односвязной области
определены в односвязной области 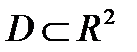 и удовлетворяют условиям:
и удовлетворяют условиям:
1)  непрерывны в
непрерывны в 
2) существуют функции 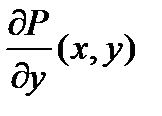 и
и  являющиеся непрерывными функциями в области
являющиеся непрерывными функциями в области 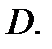
Тогда, для того чтобы выражение 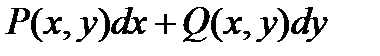 в любой точке области
в любой точке области  было полным дифференциалом некоторой функции
было полным дифференциалом некоторой функции  необходимо и достаточно выполнения условия:
необходимо и достаточно выполнения условия:

З а м е ч а н и е 4. Функция  о которой говорится в теореме 2, не единственна. Для любой другой функции вида
о которой говорится в теореме 2, не единственна. Для любой другой функции вида  где
где  постоянное число, ее полный дифференциал также совпадает с выражением
постоянное число, ее полный дифференциал также совпадает с выражением 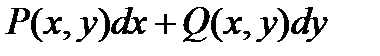 .
.
П р и м е р 5. Найти полный дифференциал второго порядка функции

Р е ш е н и е. Находим частные производные первого порядка:

Далее вычисляем все частные производные второго порядка:

Следовательно, воспользовавшись формулой (1), находим:


О т в е т: 
П р и м е р 6. Найти второй дифференциал функции 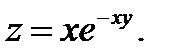
Р е ш е н и е. Последовательно находим:

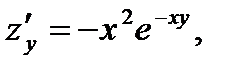

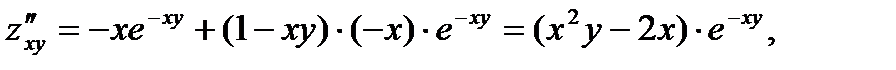
 .
.
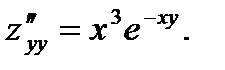
Так как в данном случае  независимые переменные, то по формуле (1) находим:
независимые переменные, то по формуле (1) находим:

О т в е т: 
П р и м е р 7. Найти функцию, полный дифференциал которой равен выражению: 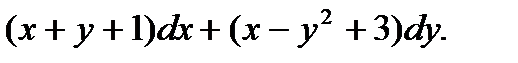
Р е ш е н и е. В данном примере
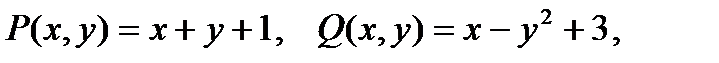

Поэтому в любой точке плоскости 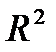 функции
функции  и
и 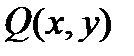 удовлетворяют всем условиям теоремы 2, а значит,
удовлетворяют всем условиям теоремы 2, а значит,  существует.
существует.
Для построения функции  воспользуемся следующей схемой:
воспользуемся следующей схемой:
1) Составим систему:
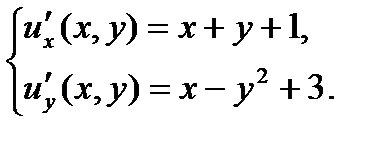 (3)
(3)
2) Проинтегрируем по  первое уравнение этой системы, считая у постоянной величиной:
первое уравнение этой системы, считая у постоянной величиной:
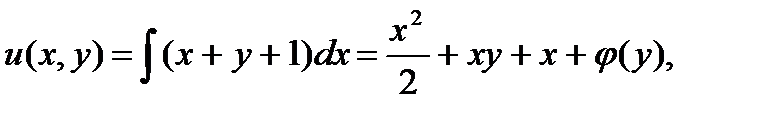 (4)
(4)
где 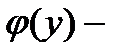 константа интегрирования.
константа интегрирования.
3) Подставим функцию  из (4) во второе уравнение системы (3):
из (4) во второе уравнение системы (3):
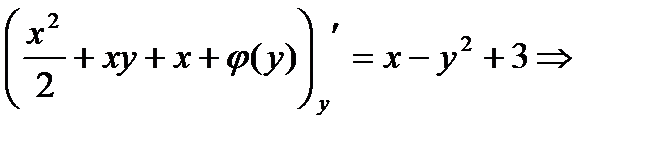
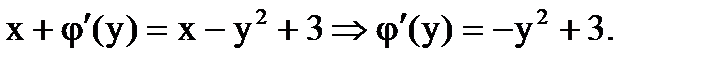
4) Решим полученное уравнение:
 (5)
(5)
где  произвольная постоянная.
произвольная постоянная.
5) Найдем функцию 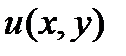 , подставив (5) в (4):
, подставив (5) в (4): 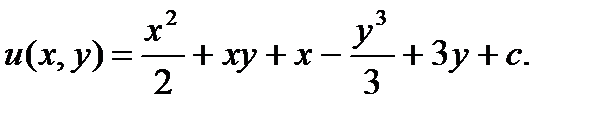
О т в е т: 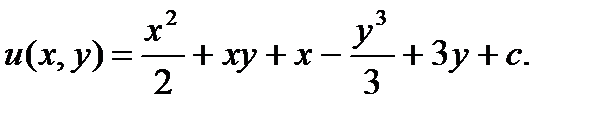
ПРИМЕРЫ
Найти частные производные второго порядка функции:
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6.  7.
7.  8.
8. 
9.  Проверить равенство:
Проверить равенство: 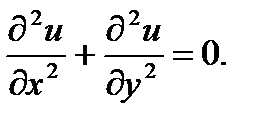
10. Доказать, что  если
если 
Найти дифференциалы второго порядка функции:
11.  12.
12. 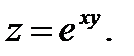 13.
13. 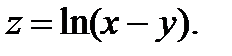 14.
14.  15.
15. 
Восстановить функцию по ее полному дифференциалу:
16.  17.
17. 
18  19.
19. 
20. 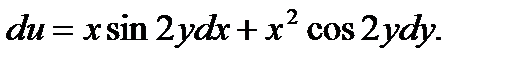 21.
21.  22.
22. 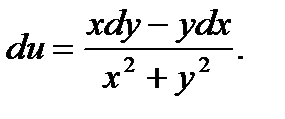
ОТВЕТЫ
1. 
2. 
3. 
4. 
5. 
6. 
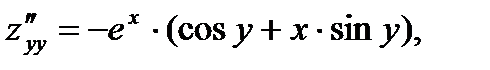
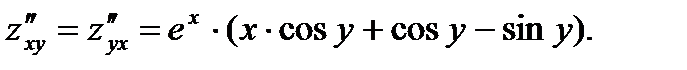
7.  8.
8. 
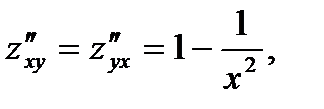

11.  12.
12. 
13.  14.
14. 
15.  16.
16. 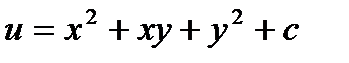 .
.
17.  . 18.
. 18.  . 19.
. 19.  .
.
20.  . 21.
. 21. 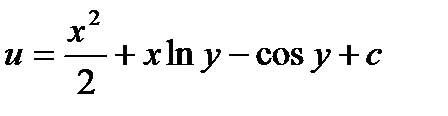 . 22.
. 22.  .
.
§ 6. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ. ГРАДИЕНТ
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Во избежание громоздких обозначений ограничимся рассмотрением, например, случая функции трех переменных.
Пусть  – область в трехмерном пространстве. Рассмотрим в области
– область в трехмерном пространстве. Рассмотрим в области 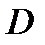 функцию
функцию 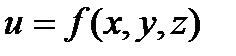 и некоторую фиксированную точку
и некоторую фиксированную точку  . Пусть
. Пусть  – некоторый ненулевой трехмерный вектор.
– некоторый ненулевой трехмерный вектор.
Проведем через точку  луч
луч 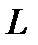 в направлении вектора
в направлении вектора  и рассмотрим функцию
и рассмотрим функцию 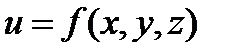 только в тех точках
только в тех точках  , которые попадают на этот луч.
, которые попадают на этот луч.
Пусть  . Тогда
. Тогда  – приращение функции
– приращение функции  в точке
в точке  по направлению вектора
по направлению вектора  .
.
О п р е д е л е н и е 1. Производной функции  в точке
в точке  по направлению вектора
по направлению вектора  называется конечный предел (если он существует) отношения приращения функции
называется конечный предел (если он существует) отношения приращения функции  к расстоянию
к расстоянию  при условии, что
при условии, что  и
и 
Используется обозначение:  Следовательно, имеем:
Следовательно, имеем:
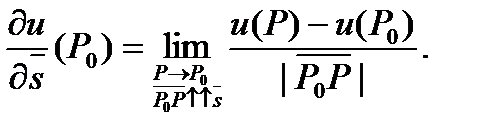 (1)
(1)
Т е о р е м а 1. Пусть функция  дифференцируема в точке
дифференцируема в точке  . Тогда в точке
. Тогда в точке 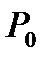 существует производная функции
существует производная функции  по направлению вектора
по направлению вектора  и справедливо равенство:
и справедливо равенство:

где 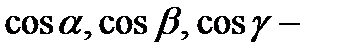 направляющие косинусы вектора
направляющие косинусы вектора 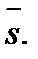
Замечание 1. Если функция 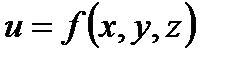 дифференцируема в точке
дифференцируема в точке  , являющейся внутренней точкой области
, являющейся внутренней точкой области  , то в точке
, то в точке  существует производная функции
существует производная функции  по любому направлению
по любому направлению 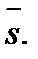 .
.
З а м е ч а н и е 2. Производные 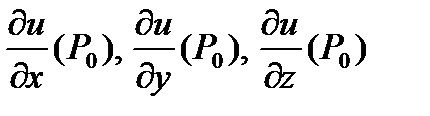 являются частными случаями производной по направлению, когда
являются частными случаями производной по направлению, когда  совпадает, соответственно, с направлением оси Ох, Оу или Оz.
совпадает, соответственно, с направлением оси Ох, Оу или Оz.
Пример 1. Для функции  найти производную в точке
найти производную в точке  в направлении вектора
в направлении вектора  , где
, где  .
.
Решение. 1) Найдем частные производные функции 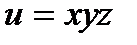 в точке
в точке  :
:
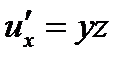 ,
,  ,
, 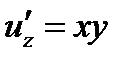 .
.
Следовательно,  ,
, 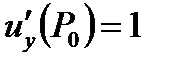 ,
,  .
.
2) Найдем направляющие косинусы вектора  . В данном случае
. В данном случае

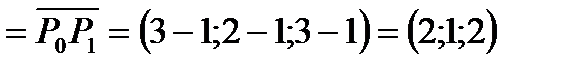 ,
,
откуда  .
.
Следовательно, 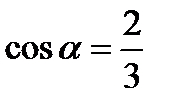 ,
,  ,
, 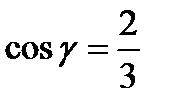 .
.
3) Найдем 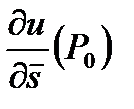 :
:
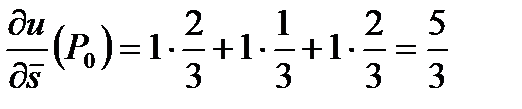 .
.
О т в е т: 
Пример 2. Для функции 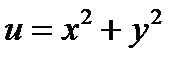 найти производную
найти производную 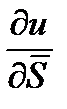 в точке
в точке 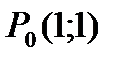 в направлении вектора
в направлении вектора
а)  ; б)
; б) 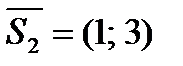 .
.
Решение. В данном случае речь идет о функции двух переменных, следовательно, в формуле (2) третье слагаемое будет отсутствовать. Во всем остальном решение примера не будет отличаться от решения примера 1.
1) Найдем частные производные функции 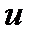 в точке
в точке  :
:
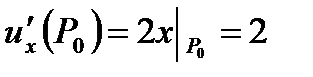 ;
;  .
.
2) Найдем направляющие косинусы векторов 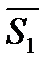 и
и  .
.
В данном случае 
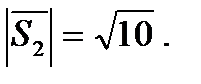 Следовательно, получаем:
Следовательно, получаем:
 для вектора
для вектора  ;
;
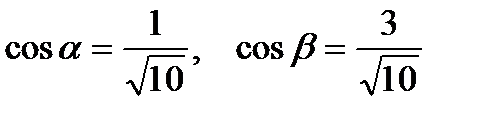 для вектора
для вектора  .
.
3) Найдем  и
и 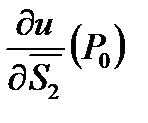 :
:
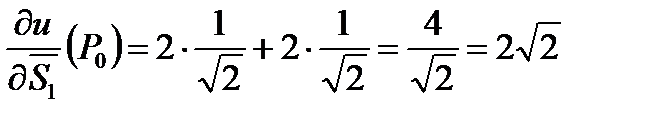 ,
,  .
.
Ответ: а)  ; б)
; б)  .
.
П р и м е р 3. Найти производную функции 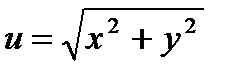 в точке
в точке  по направлению а) биссектрисы I координатного угла;
по направлению а) биссектрисы I координатного угла;
б) радиуса-вектора точки  в) вектора
в) вектора 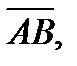 где
где 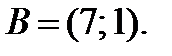
Р е ш е н и е. Найдем частные производные функции 


Вычислим их в точке 


Тогда по формуле (2) находим: 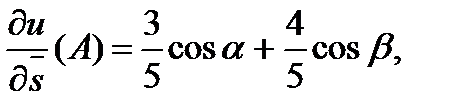
где 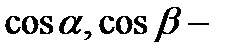 направляющие косинусы вектора
направляющие косинусы вектора 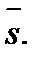
а) Для биссектрисы I координатного угла  откуда
откуда  Следовательно, получаем:
Следовательно, получаем:
 где
где 
б) В данном случае  Поэтому
Поэтому 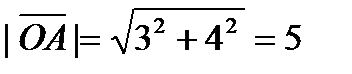 , откуда
, откуда 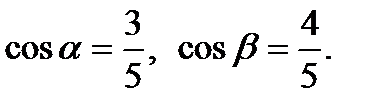 Следовательно, получаем:
Следовательно, получаем:
 где
где 
в) Так как  то
то 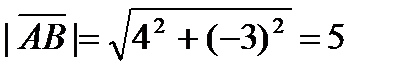 и
и  Следовательно, получаем:
Следовательно, получаем: 
О т в е т: а)  б) 1, в) 0.
б) 1, в) 0.
ГРАДИЕНТ И ЕГО СВОЙСТВА
Пусть функция  определена в области
определена в области 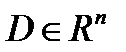 , где
, где  , дифференцируема в точке
, дифференцируема в точке 
Определение 2. Градиентом функции  в точке
в точке 
 называется
называется 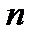 – мерный вектор, обозначаемый
– мерный вектор, обозначаемый  и вычисляемый по формуле:
и вычисляемый по формуле:
 . (3)
. (3)
В частности, если 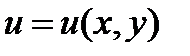 и
и 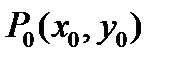 , то
, то
 ; (4)
; (4)
если  и
и 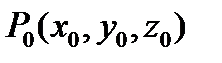
 . (5)
. (5)
Замечание 3. Для вектора (5) его направляющие косинусы вычисляются по формулам:
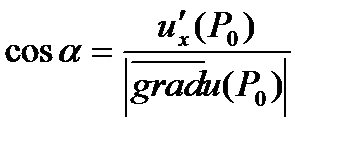 ,
,  ,
, 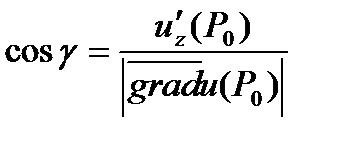 ,
,
где  .
.
Тогда формула (2) примет вид:

Свойство 1. 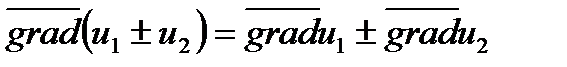 .
.
Свойство 2.  , где
, где 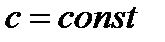 .
.
Свойство 3. Производная функции 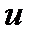 в точке
в точке  по направлению вектора
по направлению вектора  равна скалярному произведению вектора
равна скалярному произведению вектора  на единичный вектор
на единичный вектор 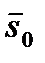 , сонаправленный с
, сонаправленный с  :
:
 , где
, где 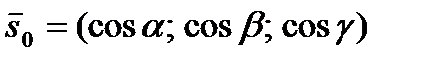 .
.
Свойство 4. Производная функции 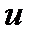 в точке
в точке  по направлению вектора
по направлению вектора  равна проекции вектора
равна проекции вектора  на вектор
на вектор  , то есть справедливо равенство:
, то есть справедливо равенство:  .
.
Свойство 5. Производная функции 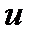 в точке
в точке  по направлению градиента функции
по направлению градиента функции 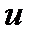 , вычисленного в точке
, вычисленного в точке  , равна длине вектора
, равна длине вектора 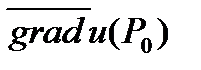 , то есть справедливо равенство:
, то есть справедливо равенство: 
С в о й с т в о 6. Производная функции 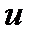 в точке
в точке 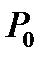 по направлению вектора
по направлению вектора  принимает наибольшее значение по сравнению с производной функции
принимает наибольшее значение по сравнению с производной функции  в точке
в точке 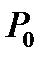 по любому другому направлению
по любому другому направлению  .
.
Свойство 7. Вектор  направлен по нормали к поверхности уровня
направлен по нормали к поверхности уровня  , где число
, где число  равно
равно  .
.
С в о й с т в о 8. Градиент не зависит от выбора системы координат.
Замечание 4. Градиент (если он не  ) функции
) функции 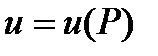 в каждой точке
в каждой точке 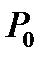 направлен в сторону наибольшего роста функции
направлен в сторону наибольшего роста функции 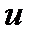 , причем скорость изменения функции
, причем скорость изменения функции 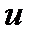 в этом направлении равна длине вектора
в этом направлении равна длине вектора  . Если
. Если 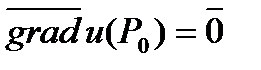 , то
, то 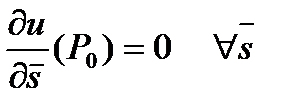 .
.
З а м е ч а н и е 5. Из свойств 6, 7 устанавливается связь между вектором 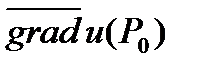 и числом
и числом  :
:
· к поверхности  , где
, где 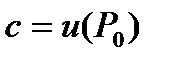 , в точке
, в точке 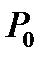 строим вектор
строим вектор  ;
;
· строим сферу, для которой |  | является диаметром;
| является диаметром;
· из точки 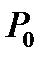 проводим вектор
проводим вектор  ;
;
· обозначим  угол между векторами
угол между векторами  и
и  ;
;
· обозначим точку пересечения вектора  с поверхностью сферы через
с поверхностью сферы через 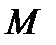 (рис.1).
(рис.1).
Тогда 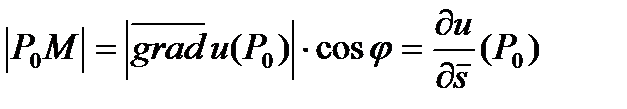 .
.
Причем, изменив направление вектора  на противоположное, производная изменит знак, но останется прежней по абсолютной величине.
на противоположное, производная изменит знак, но останется прежней по абсолютной величине.
u = c


 M
M
 Рис. 1
Рис. 1
З а м е ч а н и е 6. Для функции 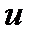 трех переменных
трех переменных
· в ц и л и н д р и ч е с к о й системе координат:
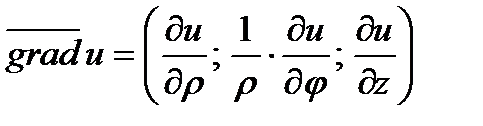 ,
,
· в с ф е р и ч е с к о й системе координат:
 .
.
Для функции  двух переменных в п о л я р н о й системе координат:
двух переменных в п о л я р н о й системе координат:
 .
.
Пример 4. Найти градиент функции 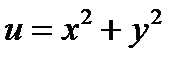 в точке
в точке 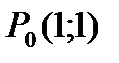 .
.
Решение. В данном случае
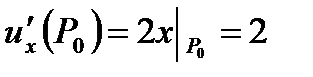 ;
;  .
.
Следовательно, получаем:
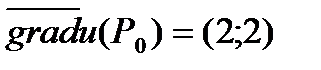 .
.
Ответ: 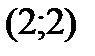 .
.
П р и м е р 5. Найти градиент функции 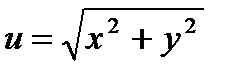 в точке
в точке 
Р е ш е н и е. Так как 
 (см. пример 3), то по формуле (3) при
(см. пример 3), то по формуле (3) при  находим:
находим:

О т в е т: 
П р и м е р 6. Найти величину наибольшей скорости изменения функции  в точке
в точке 
Р е ш е н и е. Найдем частные производные функции 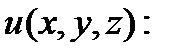

Вычислим их в точке 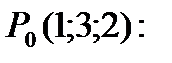
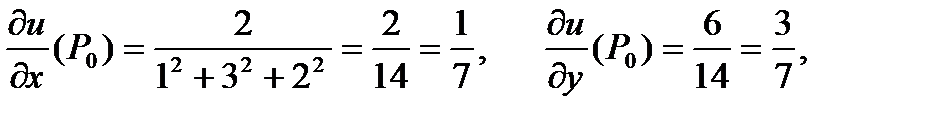
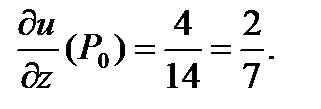
Поэтому  и
и

Следовательно, воспользовавшись свойством 7, находим наибольшее значение скорости  изменения функции
изменения функции  в точке
в точке 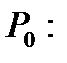
 =
= 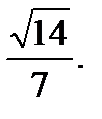
О т в е т: 
Пример 7. Найти производную функции 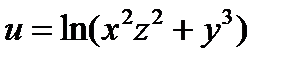 в точке
в точке 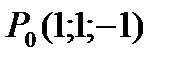 по направлению вектора
по направлению вектора 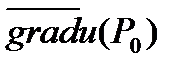 .
.
Р е ш е н и е. 1) Найдем вектор  :
:
 ,
, 
 ,
,
откуда по формуле (5) получаем:  .
.
2) Найдем:  .
.
3) Найдем по формуле (6):  .
.
Ответ:  .
.
П р и м е р 8. Найти угол между градиентами функции  в точках
в точках  и
и 
Р е ш е н и е. Найдем частные производные функции 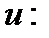

Тогда 
Следовательно 
Далее воспользуемся формулой  где
где  . Вычисляем:
. Вычисляем:

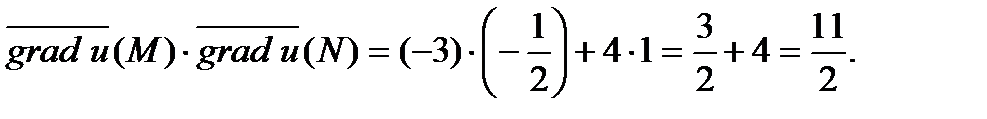
Таким образом,  где
где 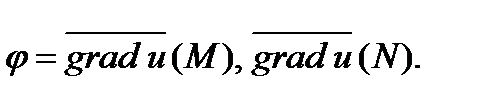
О т в е т: 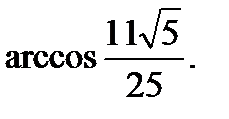
Пример 9. Найти величину и направление наибольшего роста функции 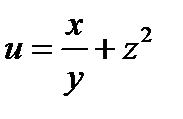 в точке
в точке  .
.
Решение. Учитывая замечание 5, решение сводится к поиску  и вычислению числа
и вычислению числа  .
.
В данном случае  ;
;  ;
; 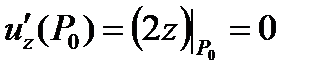 .
.
Следовательно,  ,
, 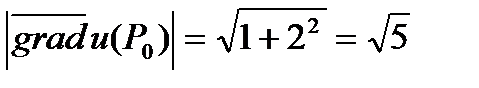 .
.
Ответ: величина наибольшего роста функции 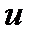 в точке
в точке 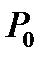 равна
равна 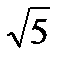 ; направление наибольшего роста функции
; направление наибольшего роста функции 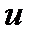 в точке
в точке 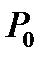 задается вектором
задается вектором 
 .
.
ПРИМЕРЫ
1. Найти производную функции  по направлению вектора
по направлению вектора  в точках
в точках 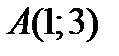 и
и 
2. Найти производную функции 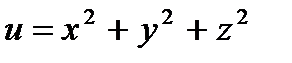 в точке
в точке  по направлению вектора а)
по направлению вектора а)  б)
б) 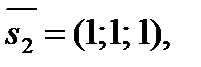 в)
в) 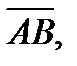 если
если  и
и 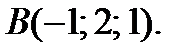
3. Найти градиент функции  в точке
в точке  и определить в точке
и определить в точке  производную функции
производную функции  по направлению вектора
по направлению вектора 
4. Для скалярного поля  найти градиент в точке
найти градиент в точке 
5. Найти производнуюфункции  в точке
в точке  по направлению ее градиента в этой точке.
по направлению ее градиента в этой точке.
6. Найти и построить градиент функции  в точках
в точках  и
и  если а)
если а)  б)
б) 
7. Найти производную функции  в точке
в точке  в направлении, составляющем с осью
в направлении, составляющем с осью 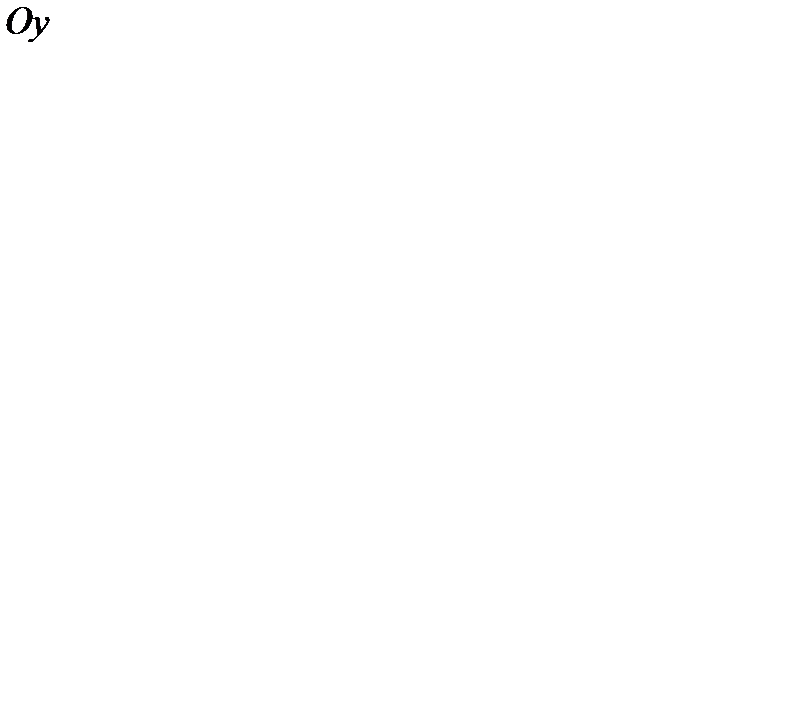 угол
угол 
8. Проверить, что в точке  производная функции
производная функции  в любом направлении равна нулю.
в любом направлении равна нулю.
9. Найти косинус угла между градиентами функции  в точках
в точках  и
и 
10. Определить, по какому направлению должна двигаться точка  при переходе через точку
при переходе через точку  чтобы функция
чтобы функция  возрастала с наибольшей скоростью.
возрастала с наибольшей скоростью.
11. Найти производную функции  в точке
в точке  в направлении градиента к поверхности
в направлении градиента к поверхности  в точке
в точке 
12. Найти производную функции  в точке
в точке  в направлении, составляющем с осями координат равные острые углы.
в направлении, составляющем с осями координат равные острые углы.
13. Найти производную функции  в точках
в точках  и
и  в направлении: а)
в направлении: а)  б)
б)  в) отрицательной полуоси Оу.
в) отрицательной полуоси Оу.
14. Найти производную функции  в точке
в точке  в направлении, идущем от
в направлении, идущем от  к точке
к точке 
15. Найти производную функции  в направлении:
в направлении:
а) биссектрисы I координатного угла, б) отрицательной полуоси Ох.
16. Найти в  и
и  градиент функции: а)
градиент функции: а)  б)
б) 
17. Для функции  найти точки, в которых ее производная по любому направлению равна нулю.
найти точки, в которых ее производная по любому направлению равна нулю.
ОТВЕТЫ
1.  2. а)
2. а)  б)
б)  в)
в)  3.
3.  4.
4.  5.
5. 
6. а)  В точке
В точке  линия уровня
линия уровня  градиент см. на рис. 2.
градиент см. на рис. 2.
у
1 B
О 1 2 3 х
-1 А
Рис. 2
В точке  линия уровня
линия уровня  градиент в точке
градиент в точке  см. на рис. 3.
см. на рис. 3.
у
-6 -2 О х
B -2
Рис. 3
б) 
 В точке
В точке  линия уровня
линия уровня  градиент см. на рис. 4.
градиент см. на рис. 4.
у
1
О 1 х
-1
А Рис. 4
В точке  линия уровня
линия уровня  градиент в точке
градиент в точке  см. на рис. 5.
см. на рис. 5.
у
-2 О х
B -2
-2,5 Рис. 5
7.  9.
9.  10.
10.  11. 5. 12.
11. 5. 12. 
13. а)  б)
б)  в)
в)  14.
14.  15. а)
15. а)  б)
б) 
16. а) 
 б)
б)  17.
17. 
§ 7. ЭКСТРЕМУМЫ ФУНКЦИИ
ЭКСТРЕМУМ
Пусть дана функция  где
где  , определенная на некотором множестве
, определенная на некотором множестве 
О п р е д е л е н и е 1. Точка  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  если в области D существует такая окрестность с центром в точке
если в области D существует такая окрестность с центром в точке 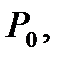 во всех
во всех



 дифференцируемую в точке
дифференцируемую в точке 
 функции
функции  в точке
в точке 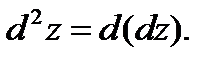
 Это – полный дифференциал от ее дифференциала (n -1)-го порядка, то есть
Это – полный дифференциал от ее дифференциала (n -1)-го порядка, то есть
 справедливы равенства:
справедливы равенства: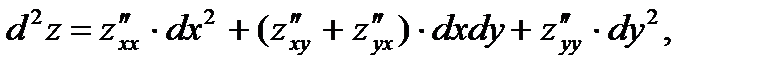 (1)
(1) независимые переменные;
независимые переменные;
 (2)
(2) и
и  дифференциал второго порядка функции
дифференциал второго порядка функции 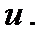
 определены в односвязной области
определены в односвязной области 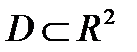 и удовлетворяют условиям:
и удовлетворяют условиям: непрерывны в
непрерывны в 
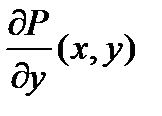 и
и  являющиеся непрерывными функциями в области
являющиеся непрерывными функциями в области 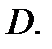
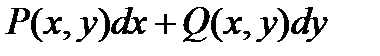 в любой точке области
в любой точке области  было полным дифференциалом некоторой функции
было полным дифференциалом некоторой функции  необходимо и достаточно выполнения условия:
необходимо и достаточно выполнения условия:
 о которой говорится в теореме 2, не единственна. Для любой другой функции вида
о которой говорится в теореме 2, не единственна. Для любой другой функции вида  где
где  постоянное число, ее полный дифференциал также совпадает с выражением
постоянное число, ее полный дифференциал также совпадает с выражением 





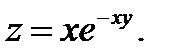

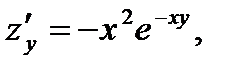

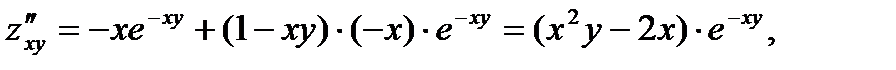
 .
.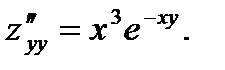
 независимые переменные, то по формуле (1) находим:
независимые переменные, то по формуле (1) находим:
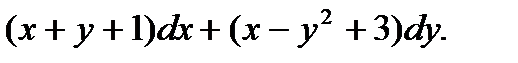
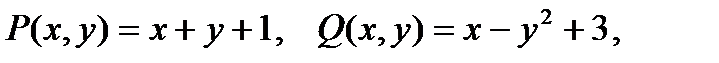

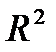 функции
функции  и
и 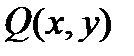 удовлетворяют всем условиям теоремы 2, а значит,
удовлетворяют всем условиям теоремы 2, а значит,  существует.
существует.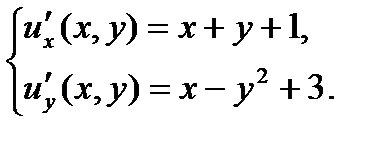 (3)
(3) первое уравнение этой системы, считая у постоянной величиной:
первое уравнение этой системы, считая у постоянной величиной: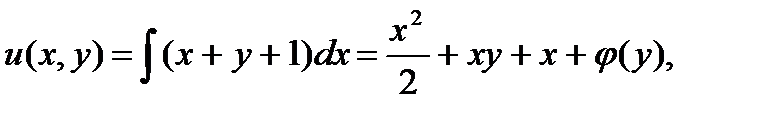 (4)
(4)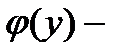 константа интегрирования.
константа интегрирования. из (4) во второе уравнение системы (3):
из (4) во второе уравнение системы (3):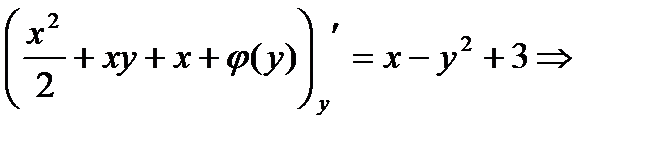
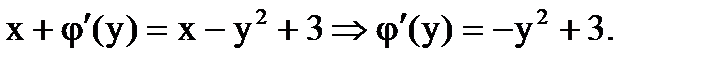
 (5)
(5) произвольная постоянная.
произвольная постоянная.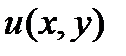 , подставив (5) в (4):
, подставив (5) в (4): 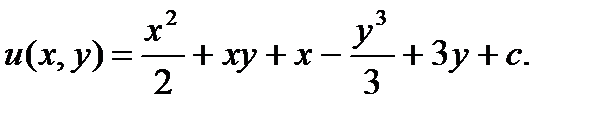
 2.
2.  3.
3.  4.
4. 
 6.
6.  7.
7.  8.
8. 
 Проверить равенство:
Проверить равенство: 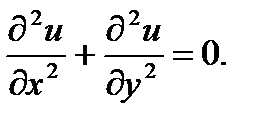
 если
если 
 12.
12. 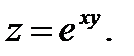 13.
13. 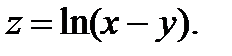 14.
14.  15.
15. 
 17.
17. 
 19.
19. 
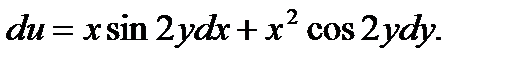 21.
21.  22.
22. 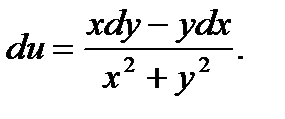






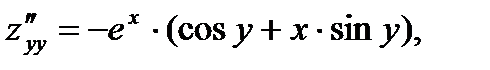
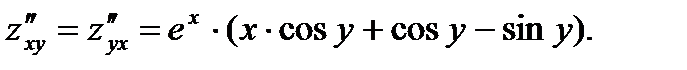
 8.
8. 
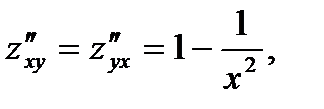

 12.
12. 
 14.
14. 
 16.
16. 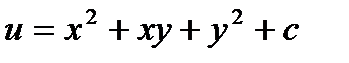 .
. . 18.
. 18.  . 19.
. 19.  .
. . 21.
. 21. 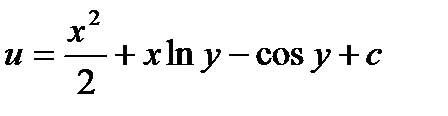 . 22.
. 22.  .
. – область в трехмерном пространстве. Рассмотрим в области
– область в трехмерном пространстве. Рассмотрим в области 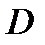 функцию
функцию 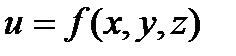 и некоторую фиксированную точку
и некоторую фиксированную точку  . Пусть
. Пусть  – некоторый ненулевой трехмерный вектор.
– некоторый ненулевой трехмерный вектор. луч
луч 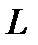 в направлении вектора
в направлении вектора 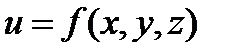 только в тех точках
только в тех точках  , которые попадают на этот луч.
, которые попадают на этот луч. . Тогда
. Тогда  – приращение функции
– приращение функции  в точке
в точке  по направлению вектора
по направлению вектора  в точке
в точке  по направлению вектора
по направлению вектора  называется конечный предел (если он существует) отношения приращения функции
называется конечный предел (если он существует) отношения приращения функции  к расстоянию
к расстоянию  при условии, что
при условии, что  и
и 
 Следовательно, имеем:
Следовательно, имеем: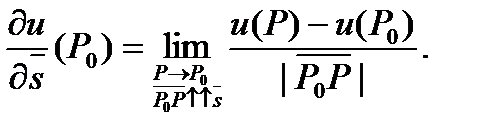 (1)
(1) дифференцируема в точке
дифференцируема в точке 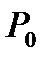 существует производная функции
существует производная функции  по направлению вектора
по направлению вектора  и справедливо равенство:
и справедливо равенство:
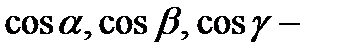 направляющие косинусы вектора
направляющие косинусы вектора 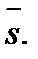
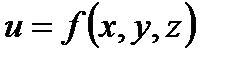 дифференцируема в точке
дифференцируема в точке  по любому направлению
по любому направлению 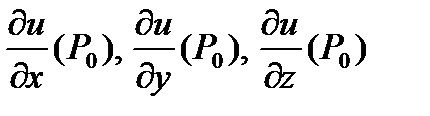 являются частными случаями производной по направлению, когда
являются частными случаями производной по направлению, когда  совпадает, соответственно, с направлением оси Ох, Оу или Оz.
совпадает, соответственно, с направлением оси Ох, Оу или Оz. найти производную в точке
найти производную в точке  в направлении вектора
в направлении вектора  , где
, где  .
.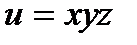 в точке
в точке 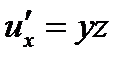 ,
,  ,
, 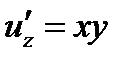 .
. ,
, 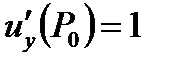 ,
,  .
.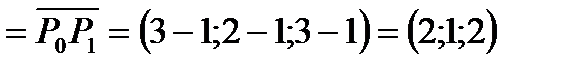 ,
, .
.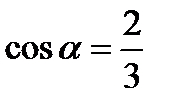 ,
,  ,
, 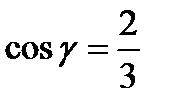 .
.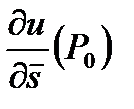 :
: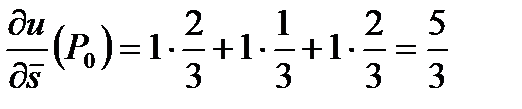 .
.
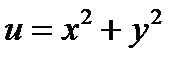 найти производную
найти производную 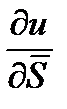 в точке
в точке 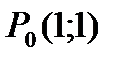 в направлении вектора
в направлении вектора ; б)
; б) 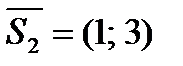 .
.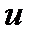 в точке
в точке 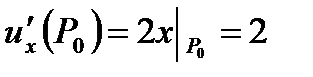 ;
;  .
.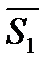 и
и  .
.
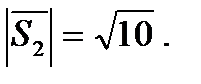 Следовательно, получаем:
Следовательно, получаем: для вектора
для вектора  ;
;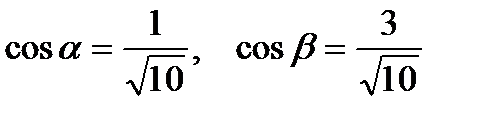 для вектора
для вектора  .
. и
и 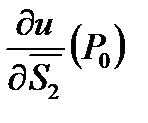 :
: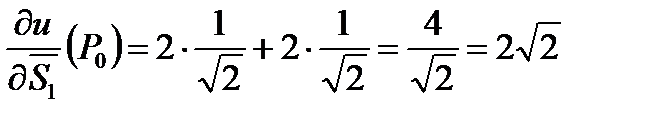 ,
,  .
. ; б)
; б)  .
.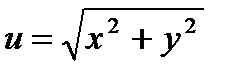 в точке
в точке  по направлению а) биссектрисы I координатного угла;
по направлению а) биссектрисы I координатного угла; в) вектора
в) вектора 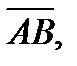 где
где 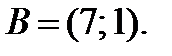






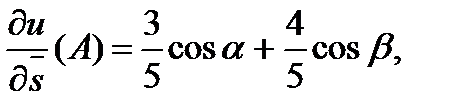
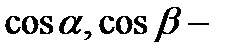 направляющие косинусы вектора
направляющие косинусы вектора 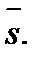
 откуда
откуда  Следовательно, получаем:
Следовательно, получаем: где
где 
 Поэтому
Поэтому 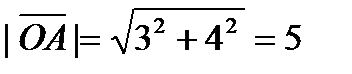 , откуда
, откуда 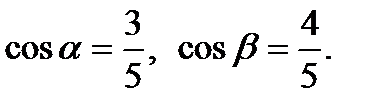 Следовательно, получаем:
Следовательно, получаем: где
где 
 то
то 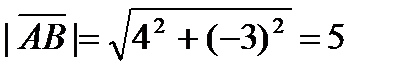 и
и  Следовательно, получаем:
Следовательно, получаем: 
 б) 1, в) 0.
б) 1, в) 0. определена в области
определена в области 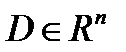 , где
, где  , дифференцируема в точке
, дифференцируема в точке 

 называется
называется 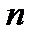 – мерный вектор, обозначаемый
– мерный вектор, обозначаемый  и вычисляемый по формуле:
и вычисляемый по формуле: . (3)
. (3)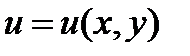 и
и 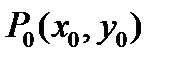 , то
, то ; (4)
; (4) и
и 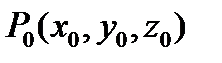
 . (5)
. (5)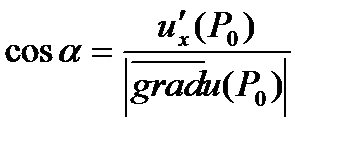 ,
,  ,
, 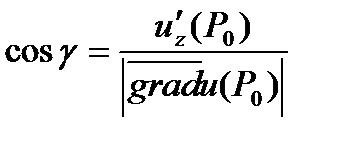 ,
, .
.
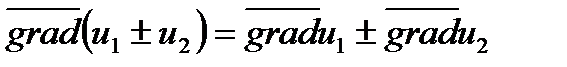 .
. , где
, где 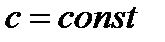 .
. по направлению вектора
по направлению вектора  равна скалярному произведению вектора
равна скалярному произведению вектора  на единичный вектор
на единичный вектор 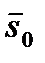 , сонаправленный с
, сонаправленный с  , где
, где 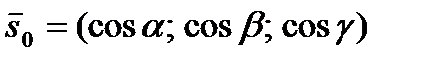 .
. на вектор
на вектор  .
.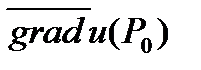 , то есть справедливо равенство:
, то есть справедливо равенство: 
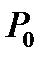 по направлению вектора
по направлению вектора  принимает наибольшее значение по сравнению с производной функции
принимает наибольшее значение по сравнению с производной функции  в точке
в точке  направлен по нормали к поверхности уровня
направлен по нормали к поверхности уровня  , где число
, где число  равно
равно  .
. ) функции
) функции 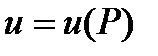 в каждой точке
в каждой точке  . Если
. Если 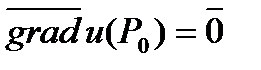 , то
, то 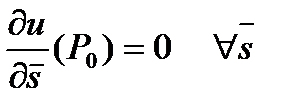 .
.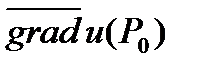 и числом
и числом  :
: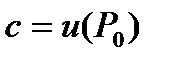 , в точке
, в точке  ;
; | является диаметром;
| является диаметром; угол между векторами
угол между векторами  и
и  (рис.1).
(рис.1).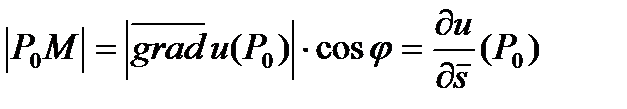 .
.
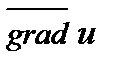

 M
M Рис. 1
Рис. 1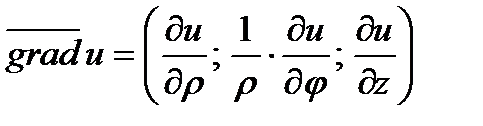 ,
, .
. двух переменных в п о л я р н о й системе координат:
двух переменных в п о л я р н о й системе координат: .
.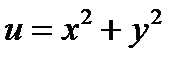 в точке
в точке 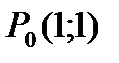 .
.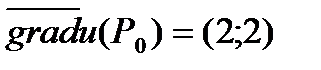 .
. .
.

 (см. пример 3), то по формуле (3) при
(см. пример 3), то по формуле (3) при  находим:
находим:

 в точке
в точке 
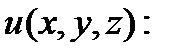

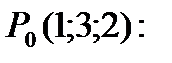
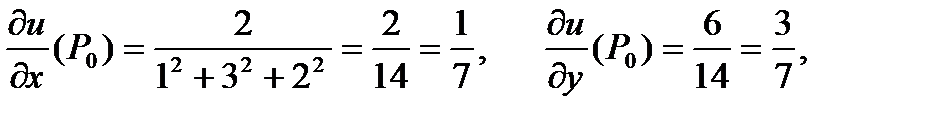
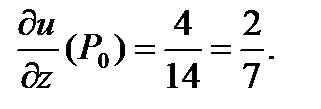
 и
и
 изменения функции
изменения функции  в точке
в точке 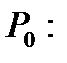
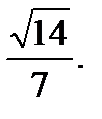

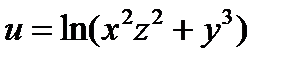 в точке
в точке 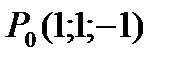 по направлению вектора
по направлению вектора 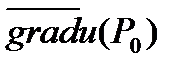 .
. :
: ,
, 
 ,
, .
. .
. .
. .
. в точках
в точках  и
и 
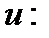



 где
где  . Вычисляем:
. Вычисляем:
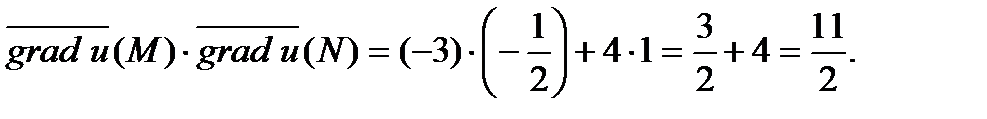
 где
где 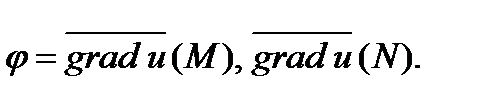
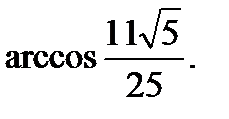
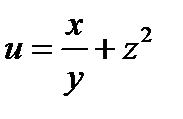 в точке
в точке  .
. и вычислению числа
и вычислению числа  .
. ;
;  ;
; 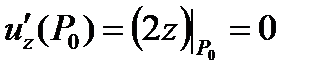 .
. ,
, 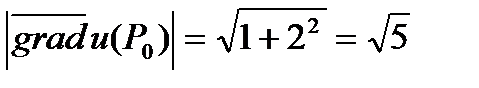 .
.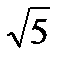 ; направление наибольшего роста функции
; направление наибольшего роста функции 
 .
. по направлению вектора
по направлению вектора  в точках
в точках 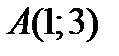 и
и 
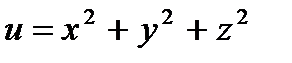 в точке
в точке  по направлению вектора а)
по направлению вектора а)  б)
б) 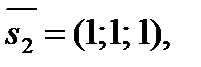 в)
в) 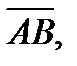 если
если  и
и 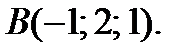
 в точке
в точке  и определить в точке
и определить в точке  производную функции
производную функции  по направлению вектора
по направлению вектора 
 найти градиент в точке
найти градиент в точке 
 в точке
в точке  по направлению ее градиента в этой точке.
по направлению ее градиента в этой точке. в точках
в точках  и
и  если а)
если а)  б)
б) 
 в точке
в точке  в направлении, составляющем с осью
в направлении, составляющем с осью 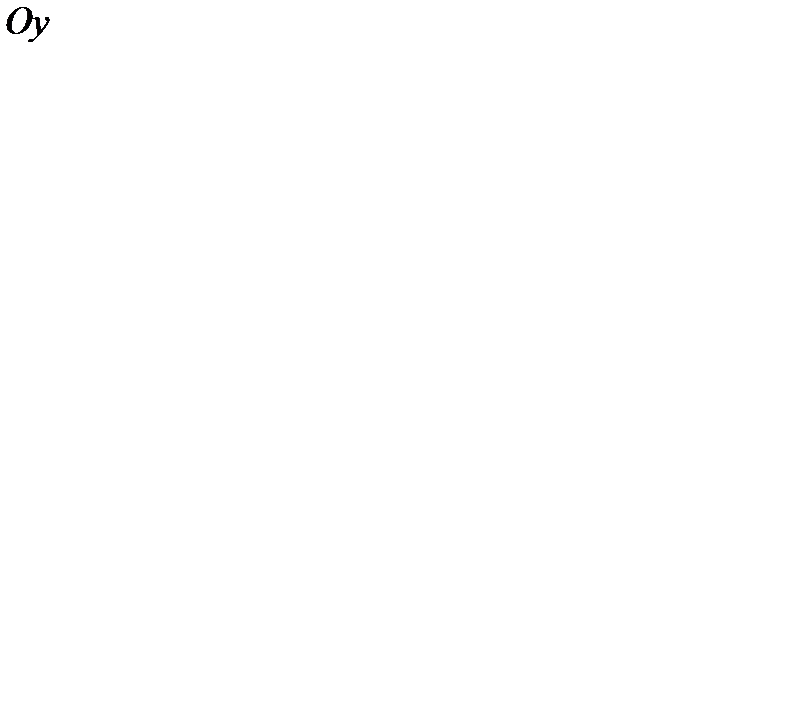 угол
угол 
 производная функции
производная функции  в любом направлении равна нулю.
в любом направлении равна нулю. в точках
в точках  и
и 
 при переходе через точку
при переходе через точку  чтобы функция
чтобы функция  возрастала с наибольшей скоростью.
возрастала с наибольшей скоростью. в точке
в точке  в направлении градиента к поверхности
в направлении градиента к поверхности  в точке
в точке 
 в точке
в точке  в направлении, составляющем с осями координат равные острые углы.
в направлении, составляющем с осями координат равные острые углы. в точках
в точках  и
и  в направлении: а)
в направлении: а)  б)
б)  в) отрицательной полуоси Оу.
в) отрицательной полуоси Оу. в точке
в точке  в направлении, идущем от
в направлении, идущем от  к точке
к точке 
 в направлении:
в направлении: и
и  градиент функции: а)
градиент функции: а)  б)
б) 
 найти точки, в которых ее производная по любому направлению равна нулю.
найти точки, в которых ее производная по любому направлению равна нулю. 2. а)
2. а)  б)
б)  в)
в)  3.
3.  4.
4.  5.
5. 
 В точке
В точке  линия уровня
линия уровня  градиент см. на рис. 2.
градиент см. на рис. 2. линия уровня
линия уровня  градиент в точке
градиент в точке 
 В точке
В точке  градиент см. на рис. 4.
градиент см. на рис. 4. градиент в точке
градиент в точке  9.
9.  10.
10.  11. 5. 12.
11. 5. 12. 
 б)
б)  в)
в)  14.
14.  15. а)
15. а)  б)
б) 

 б)
б)  17.
17. 
 где
где  , определенная на некотором множестве
, определенная на некотором множестве 
 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  если в области D существует такая окрестность с центром в точке
если в области D существует такая окрестность с центром в точке  во всех
во всех


