В ЗАМКНУТОЙ ОБЛАСТИ
В замкнутой области 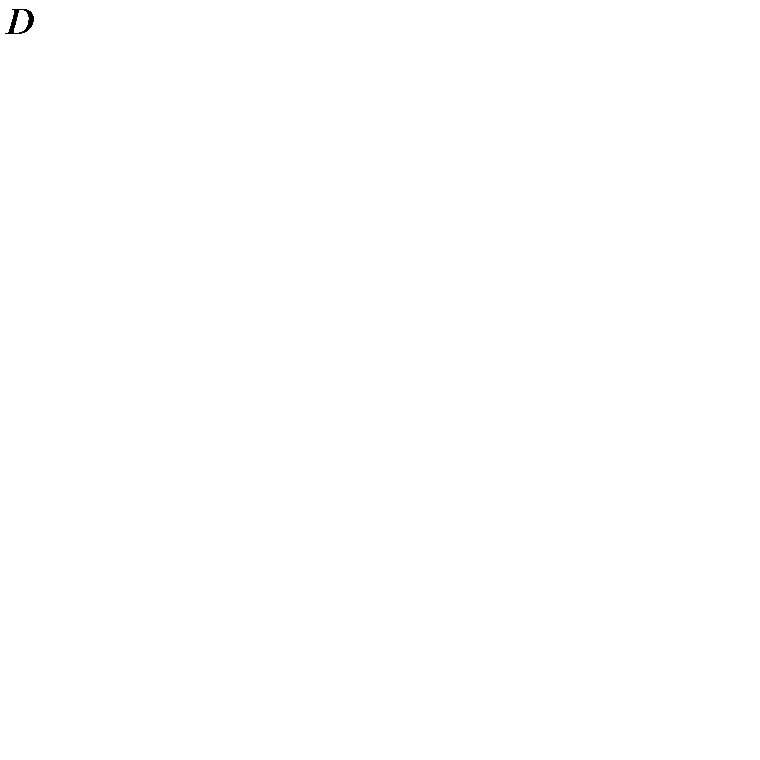 непрерывная функция
непрерывная функция  достигает наибольшего и наименьшего значений, называемых глобальными экстремумами функции
достигает наибольшего и наименьшего значений, называемых глобальными экстремумами функции  в
в 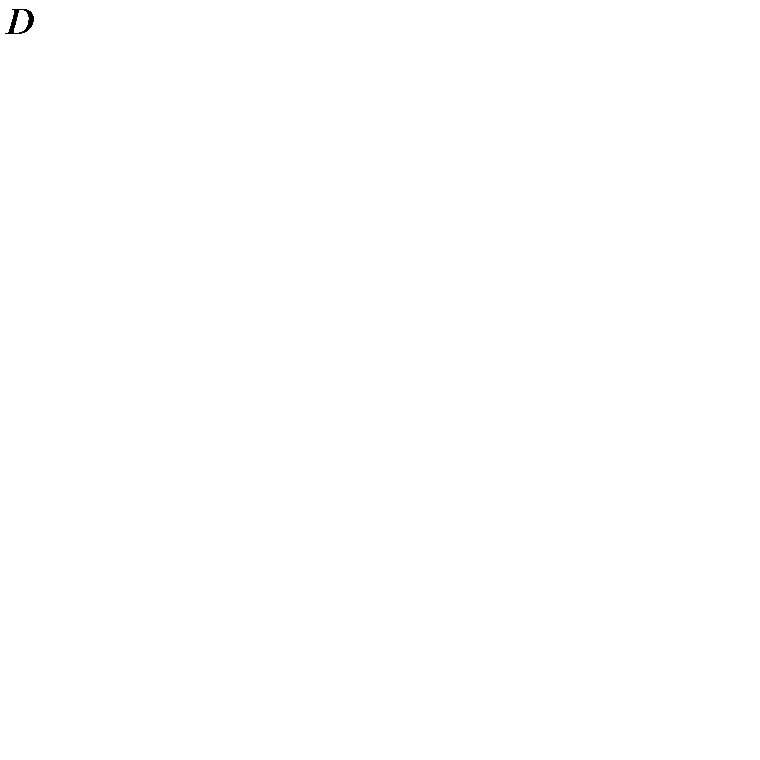 . Они достигаются либо во внутренних точках области (тогда это критические точки функции
. Они достигаются либо во внутренних точках области (тогда это критические точки функции  ), либо на границе (тогда это одни из точек, претендующих на условный экстремум функции
), либо на границе (тогда это одни из точек, претендующих на условный экстремум функции  ).
).
Схема поиска глобальных экстремумов:
· Найти критические точки функции  , являющиеся внутренними точками области
, являющиеся внутренними точками области 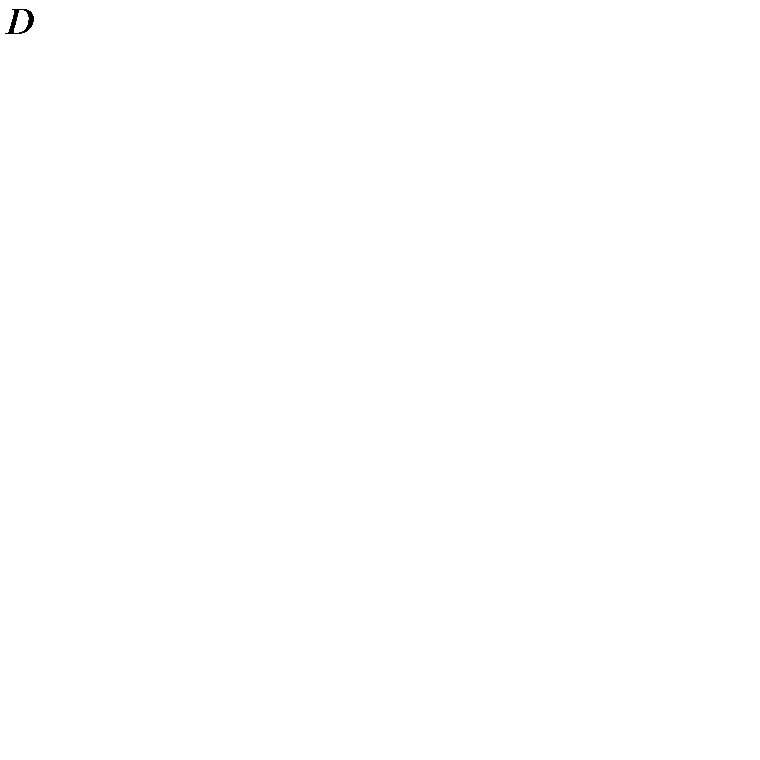 ;
;
· найти точки на границе области 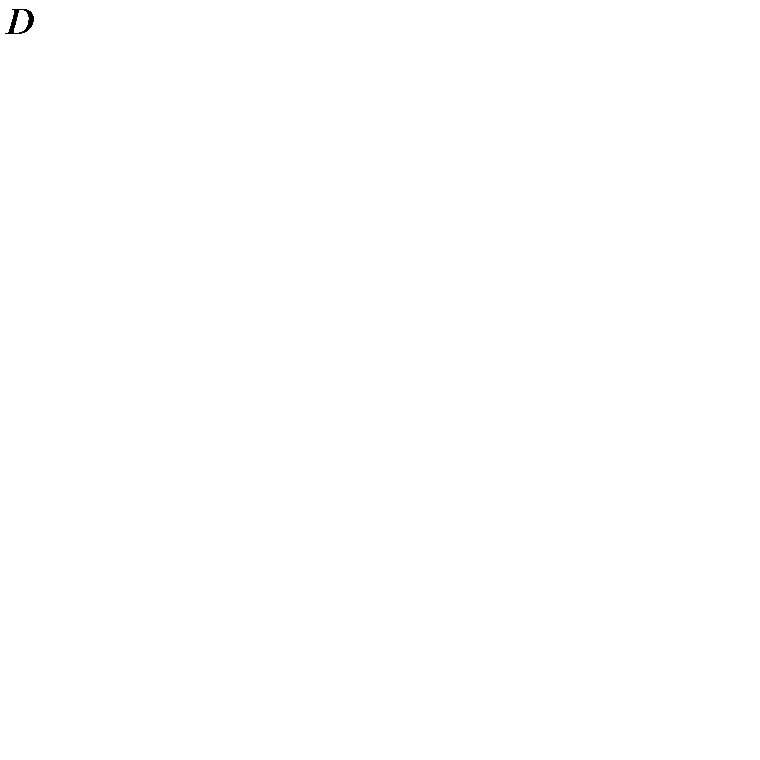 , «подозрительные» на условный экстремум функции
, «подозрительные» на условный экстремум функции 
· вычислить значения функции  в каждой из найденных точек;
в каждой из найденных точек;
· из полученных чисел выбрать наибольшее (обозначаемое  или
или  ) и наименьшее (обозначаемое
) и наименьшее (обозначаемое  или
или  ).
).
П р и м е р 5. Найти наибольшее и наименьшее значения функции

в области 
Р е ш е н и е. Область  изображена на рисунке.
изображена на рисунке.
у
3
х=0 у =3- х
О у =0 3 х
1) Найдем критические точки функции  внутри области
внутри области 
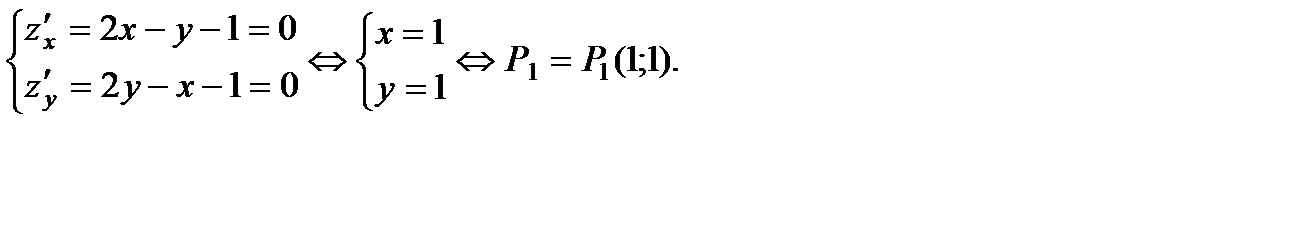
2) Найдем критические точки сужения функции  на границе
на границе 
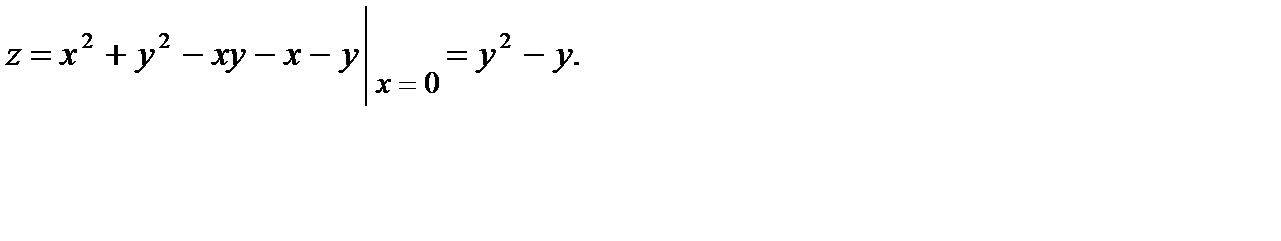
Поэтому  откуда
откуда 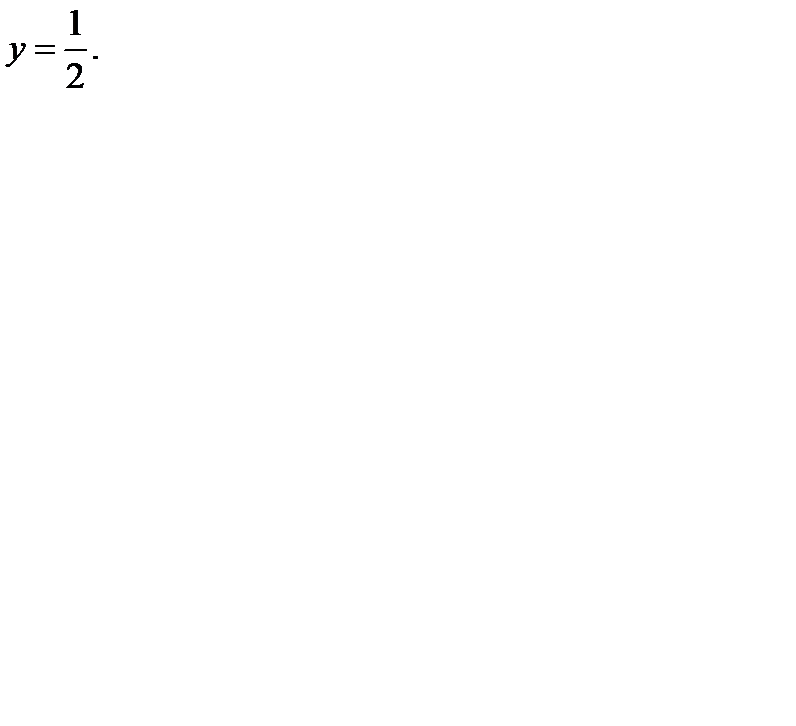 Следовательно,
Следовательно, 
3) Найдем критические точки сужения функции  на границе
на границе 
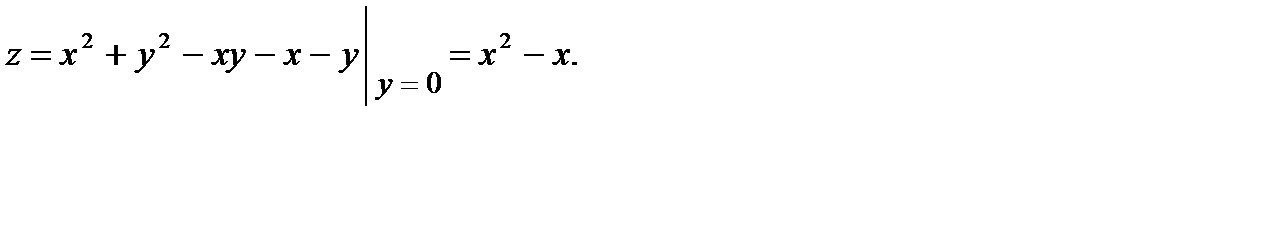
Поэтому  откуда
откуда 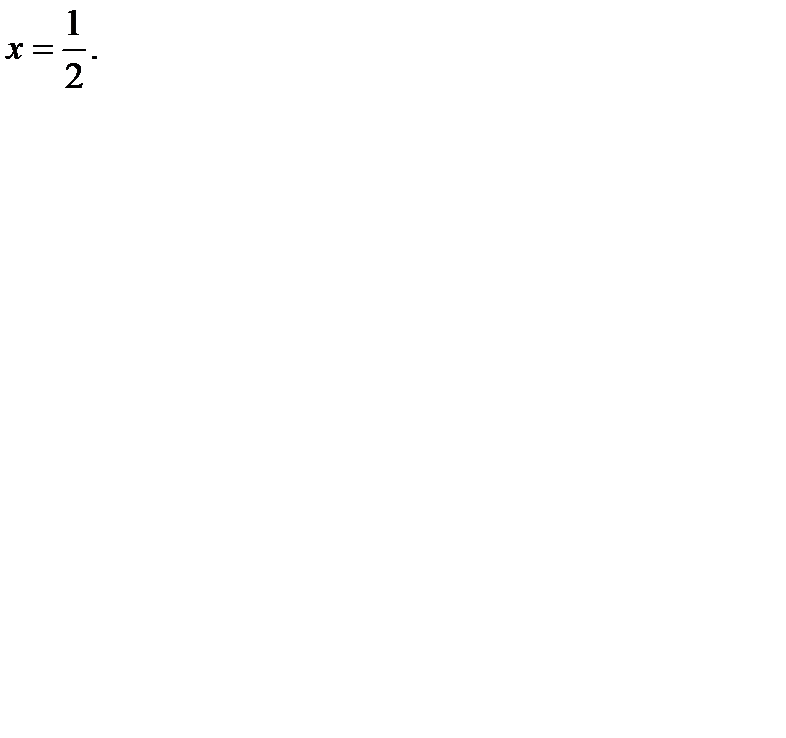 Следовательно,
Следовательно, 
4) Найдем критические точки сужения функции  на границе
на границе 
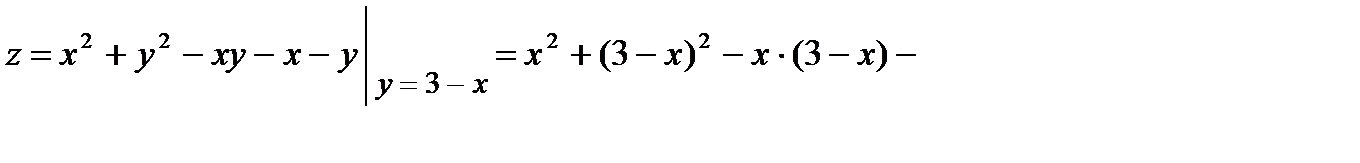

Так как  , то
, то  . При этом
. При этом  Следовательно,
Следовательно, 
5) Вычислим функцию  в точках
в точках  и «угловых» точках границы:
и «угловых» точках границы: 




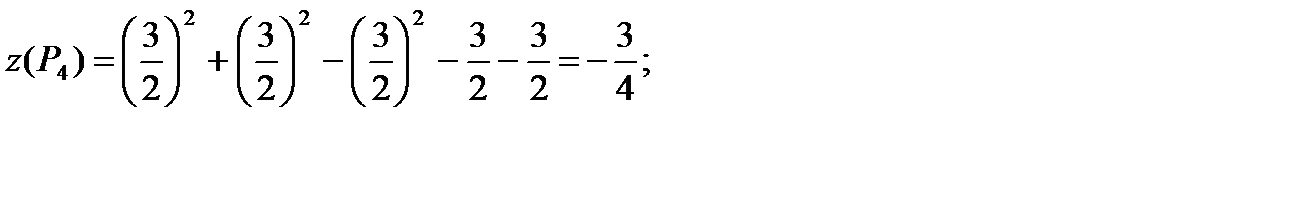



Из полученных семи чисел выбираем наибольшее и наименьшее:


О т в е т: наибольшее значение функции  в области
в области  равно 6 и достигается в точках
равно 6 и достигается в точках  наименьшее значение функции
наименьшее значение функции  в области
в области  равно -1 и достигается в точке
равно -1 и достигается в точке 
ПРИМЕРЫ
Определить условные экстремумы функций:
1.  при
при  2.
2.  при
при 
3.  при
при  4.
4. 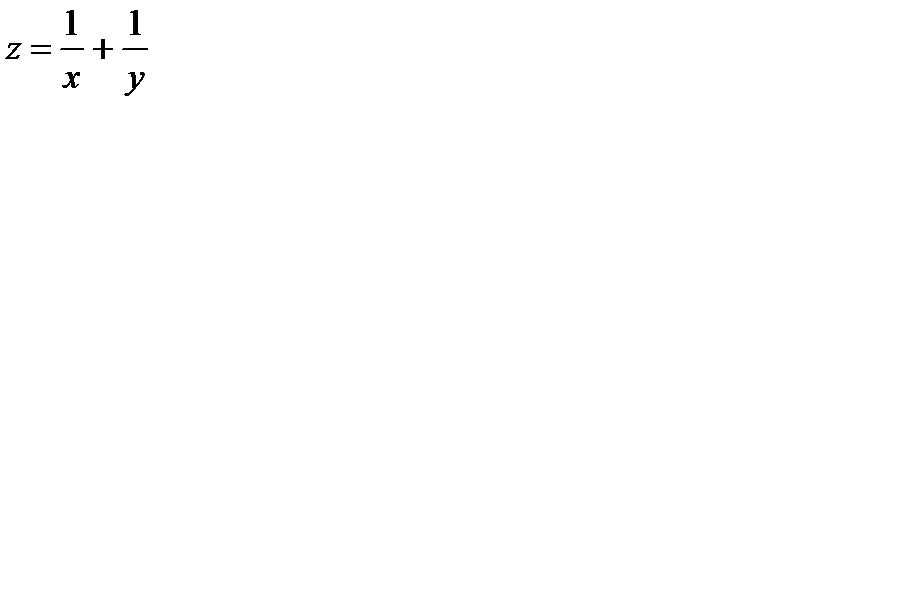 при
при 
5..  при
при  6.
6.  при
при 
7. Из всех треугольников с одинаковым периметром  определить тот, площадь которого наибольшая.
определить тот, площадь которого наибольшая.
8. Найти наибольшее и наименьшее значения функции  в треугольнике
в треугольнике  если
если 
9. Найти наибольшее и наименьшее значения функции  в области
в области  и
и  .
.
ОТВЕТЫ
1.  при
при  2.
2.  при
при 
3.  при
при 
 при
при 
4.  при
при  5.
5.  при
при 
 при
при 
6.  при
при  7. Равносторонний треугольник со стороной
7. Равносторонний треугольник со стороной 
8.  во всех точках отрезков
во всех точках отрезков  и
и 
 при
при 
9.  при
при 
 при
при 
§ 9. ДВОЙНОЙ ИНТЕГРАЛ
1. ОПРЕДЕЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Рассмотрим функцию 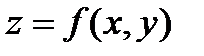 (или
(или 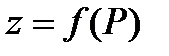 ), определенную в некоторой замкнутой области
), определенную в некоторой замкнутой области 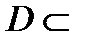
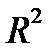 . Разобьем область
. Разобьем область 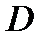 какими-нибудь линиями на
какими-нибудь линиями на 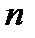 областей
областей 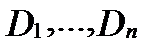 , которые могут пересекаться только по своим границам. Обозначим площадь области
, которые могут пересекаться только по своим границам. Обозначим площадь области 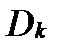 через
через 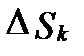 . Тогда
. Тогда
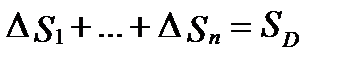 , где
, где 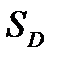 - площадь области
- площадь области 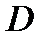 .
.
В каждой из областей 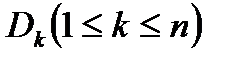 выберем произвольным образом точку
выберем произвольным образом точку 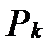 . Вычислим значение
. Вычислим значение 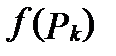 функции
функции 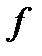 в точке
в точке 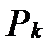 .
.
Определение 1. Сумма вида
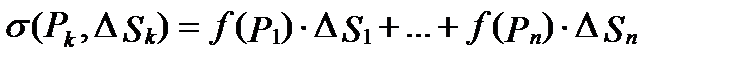 (1)
(1)
называется двойной интегральной суммой для функции 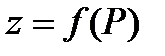 в области
в области 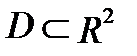 . Число
. Число 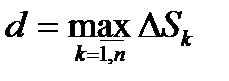 называется диаметром разбиения области
называется диаметром разбиения области 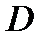 на части.
на части.
Определение 2. Если существует конечный предел двойной интегральной суммы (1) при стремлении диаметра разбиения к нулю и этот предел не зависит ни от способа разбиения области 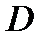 на части, ни от выбора в них промежуточных точек
на части, ни от выбора в них промежуточных точек 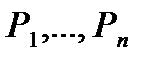 , то этот предел называется двойным интегралом от функции
, то этот предел называется двойным интегралом от функции 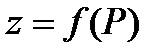 по области
по области 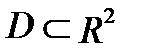 , а сама функция называется интегрируемой в области
, а сама функция называется интегрируемой в области 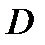 .
.
Для двойного интеграла используется обозначение: 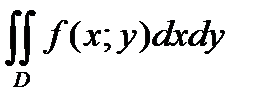 . Тогда
. Тогда
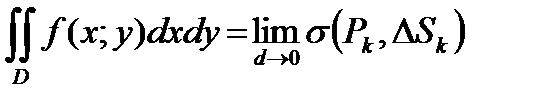 . (2)
. (2)
Теорема 1 (достаточное условие существования двойного интеграла).Пусть функция 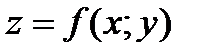 непрерывна в замкнутой области
непрерывна в замкнутой области 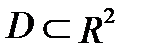 . Тогда она интегрируема на области
. Тогда она интегрируема на области 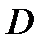 и существует ее двойной интеграл по области
и существует ее двойной интеграл по области 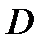 .
.
Пусть функция 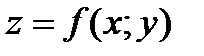 непрерывна в области
непрерывна в области 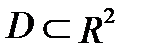 и
и
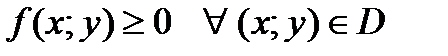 .
.
Тогда в формуле (1) слагаемое 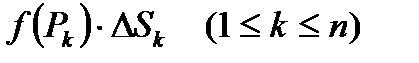 представляет собой с геометрической точки зрения объем цилиндрического тела с основанием
представляет собой с геометрической точки зрения объем цилиндрического тела с основанием 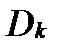 , площадь которого
, площадь которого 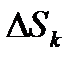 , и высотой
, и высотой 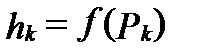 .
.
Двойная интегральная сумма (1), как сумма объемов указанных элементарных цилиндров, равна объему 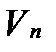 некоторого ступенчатого цилиндрического тела. Тогда предел (2) при
некоторого ступенчатого цилиндрического тела. Тогда предел (2) при 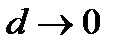 (то есть
(то есть 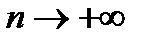 ) совпадает с объемом
) совпадает с объемом 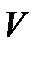 тела, ограниченного снизу областью
тела, ограниченного снизу областью 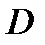 , сверху – поверхностью
, сверху – поверхностью 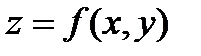 , сбоку - цилиндрической поверхностью, образующие которой параллельны оси
, сбоку - цилиндрической поверхностью, образующие которой параллельны оси 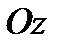 , а направляющей служит граница области
, а направляющей служит граница области 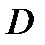 .
.
Замечание 1. Если непрерывная функция 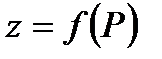 не сохраняет знак в области
не сохраняет знак в области 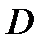 , то двойной интеграл
, то двойной интеграл 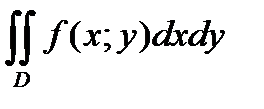 с геометрической точки зрения есть алгебраическая сумма объемов, учитываемых с «+» или «-» в зависимости от того, лежит поверхность
с геометрической точки зрения есть алгебраическая сумма объемов, учитываемых с «+» или «-» в зависимости от того, лежит поверхность 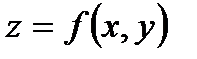 выше или ниже плоскости
выше или ниже плоскости 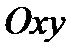 .
.
СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
На двойные интегралы переносятся все основные свойства обыкновенного (однократного) определенного интеграла.
Свойство 1. Пусть функция 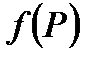 интегрируема в области
интегрируема в области 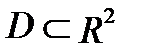 , где
, где 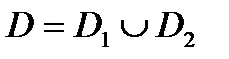 и
и 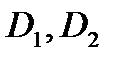 пересекаются только по своим границам. Тогда функция
пересекаются только по своим границам. Тогда функция 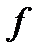 интегрируема отдельно в
интегрируема отдельно в 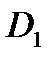 и в
и в 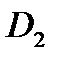 , причем справедливо равенство:
, причем справедливо равенство:
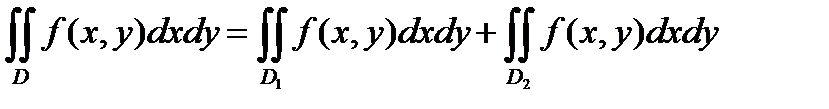 .
.
Свойство 2. Если функции 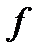 и
и 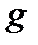 интегрируемы в области
интегрируемы в области 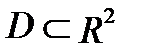 , то в
, то в 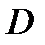 будут интегрируемы также следующие функции:
будут интегрируемы также следующие функции:
1) 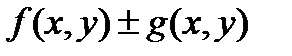 ;
;
2) 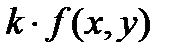 , где
, где 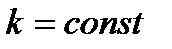 ;
;
3) 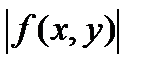 ;
;
4) 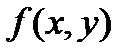
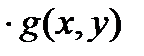 ;
;
5) 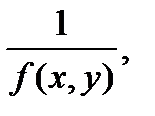 если
если 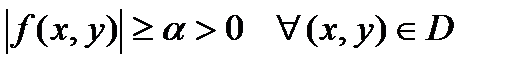 .
.
При этом для функций 1) – 3) справедливы соотношения:
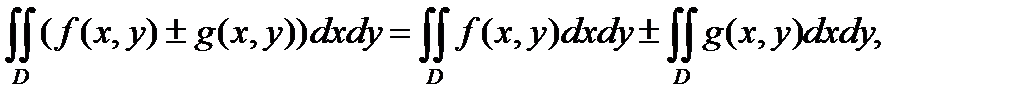
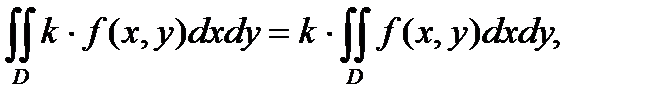
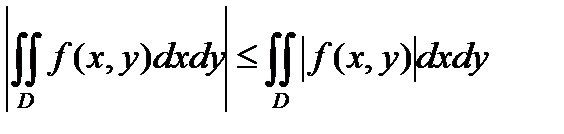 .
.
С в о й с т в о 3. Если функции 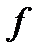 и
и 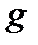 интегрируемы в области
интегрируемы в области 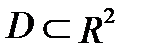 и
и 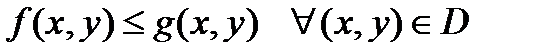 , то справедливо неравенство:
, то справедливо неравенство:
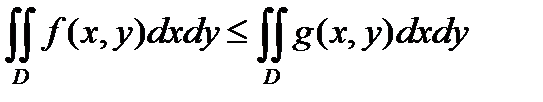 .
.
С в о й с т в о 4. Если функция 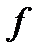 интегрируема в области
интегрируема в области 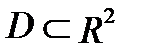 и
и 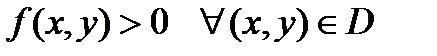 , то справедливо неравенство:
, то справедливо неравенство:
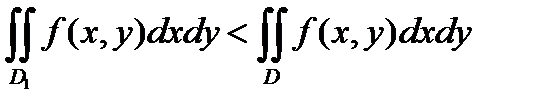 , если
, если 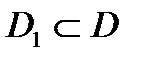 .
.
С в о й с т в о 5. 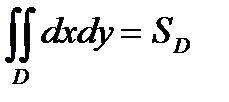 , где
, где 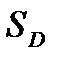 - площадь области
- площадь области 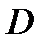 .
.
С в о й с т в о 6. 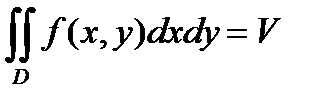 , где
, где 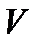 - объем тела, ограниченного снизу областью
- объем тела, ограниченного снизу областью 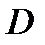 , принадлежащей плоскости
, принадлежащей плоскости 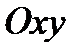 , сверху - поверхностью
, сверху - поверхностью 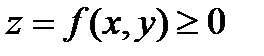 , сбоку - цилиндрической поверхностью, образующие которой параллельны оси
, сбоку - цилиндрической поверхностью, образующие которой параллельны оси 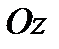 , а направляющей служит граница области
, а направляющей служит граница области 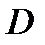 .
.
Свойство 7 (о среднем значении). Пусть функция 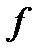 непрерывна в области
непрерывна в области 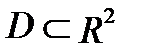 . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка 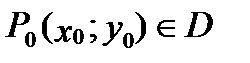 , в которой выполняется равенство:
, в которой выполняется равенство: 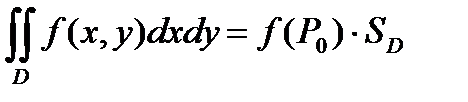 .
.
З а м е ч а н и е 2. Если дополнительно 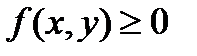
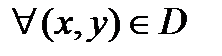 , то с геометрической точки зрения из свойства 7 заключаем: двойной интеграл от функции
, то с геометрической точки зрения из свойства 7 заключаем: двойной интеграл от функции 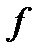 по области
по области 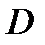 равен объему некоторого цилиндра с основанием
равен объему некоторого цилиндра с основанием 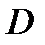 , высотой
, высотой 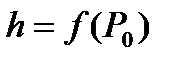 , где
, где 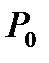 - определенная точка из
- определенная точка из 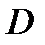 , с образующими, параллельными оси
, с образующими, параллельными оси 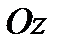 и выходящими из точек границы области
и выходящими из точек границы области 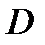 .
.



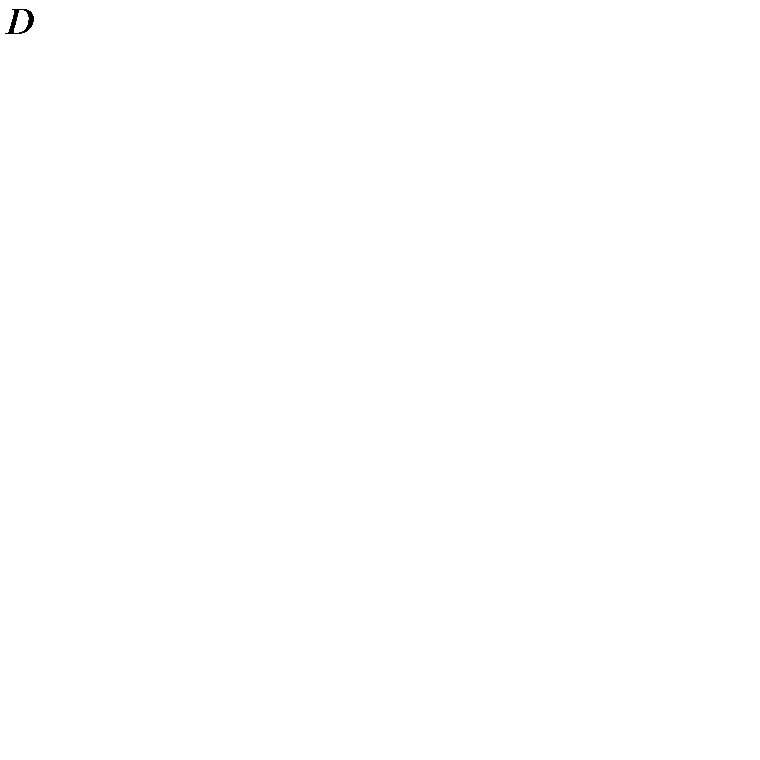 непрерывная функция
непрерывная функция  достигает наибольшего и наименьшего значений, называемых глобальными экстремумами функции
достигает наибольшего и наименьшего значений, называемых глобальными экстремумами функции  в
в 
 или
или  ) и наименьшее (обозначаемое
) и наименьшее (обозначаемое  или
или  ).
).

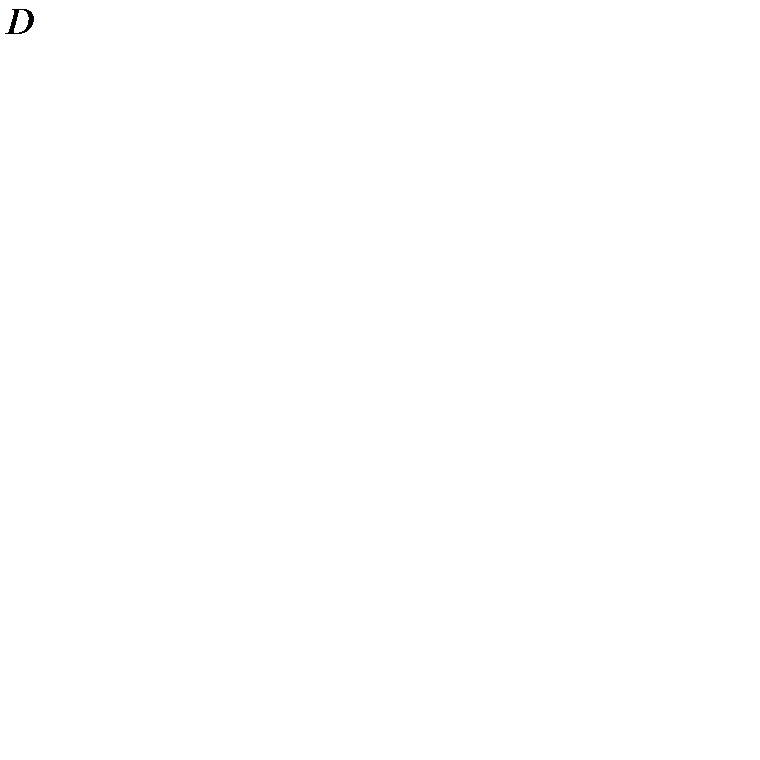 изображена на рисунке.
изображена на рисунке. внутри области
внутри области 
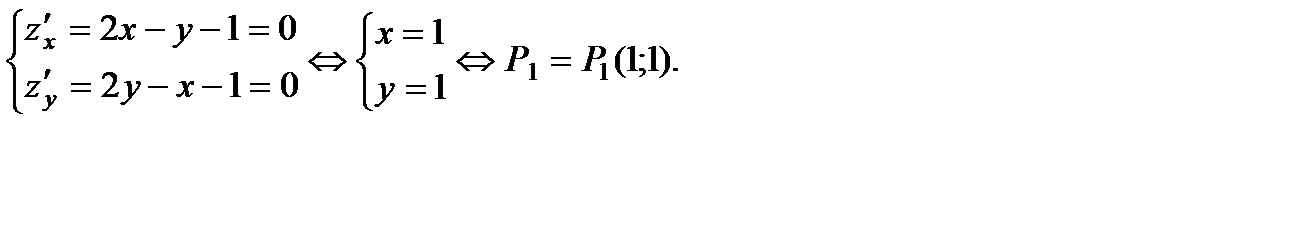

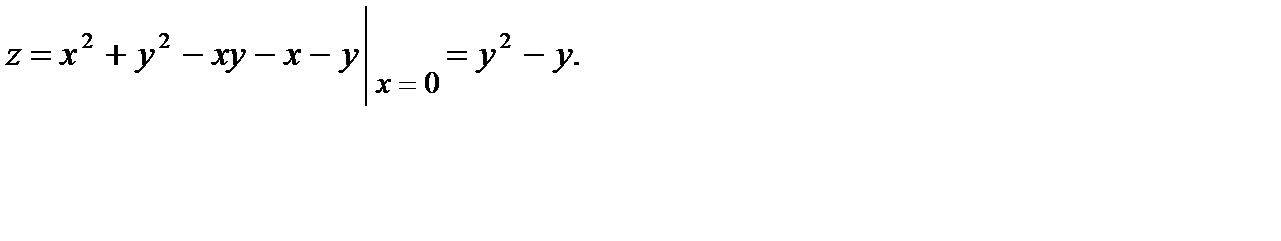
 откуда
откуда 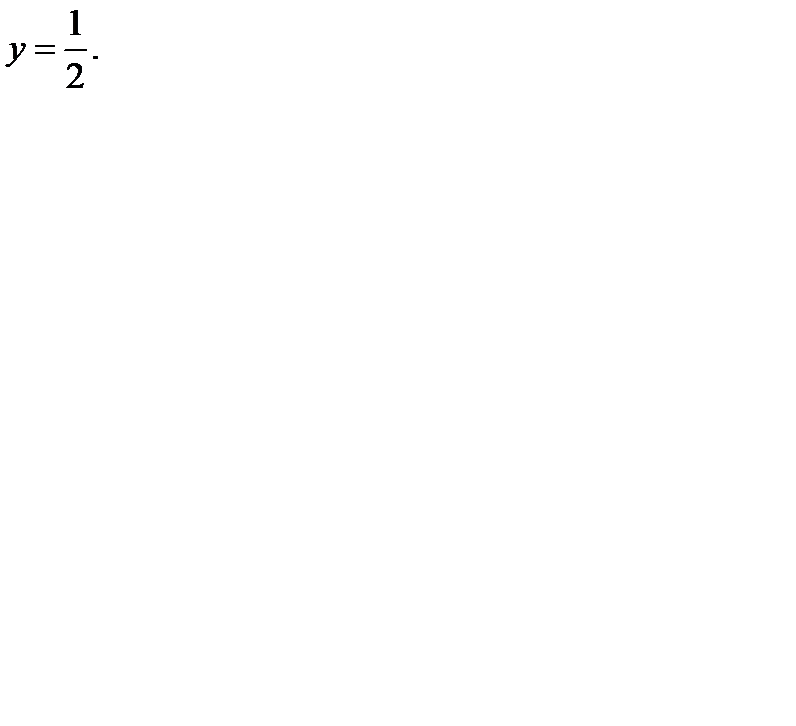 Следовательно,
Следовательно, 

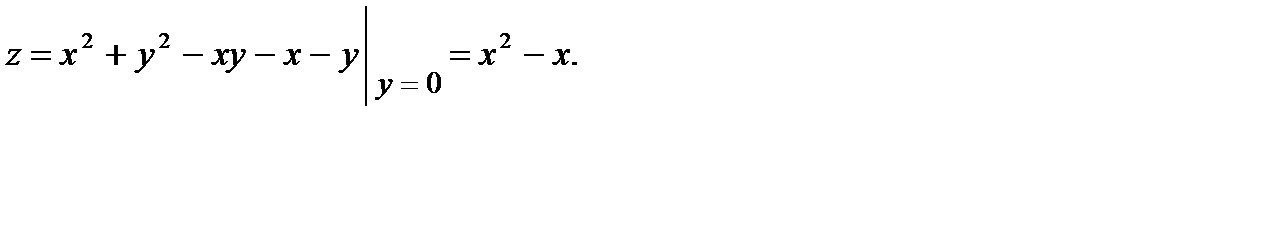
 откуда
откуда 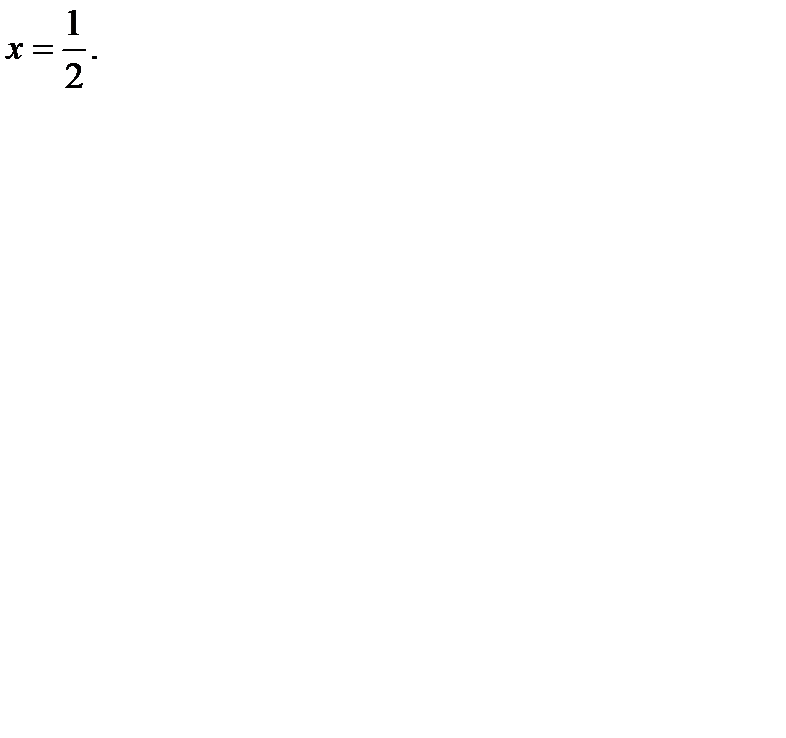 Следовательно,
Следовательно, 

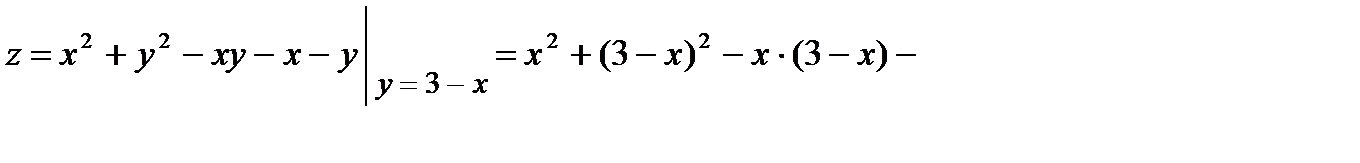

 , то
, то  . При этом
. При этом  Следовательно,
Следовательно, 
 и «угловых» точках границы:
и «угловых» точках границы: 




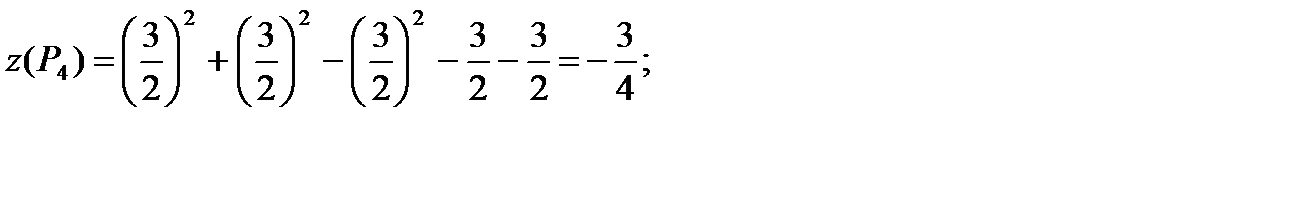





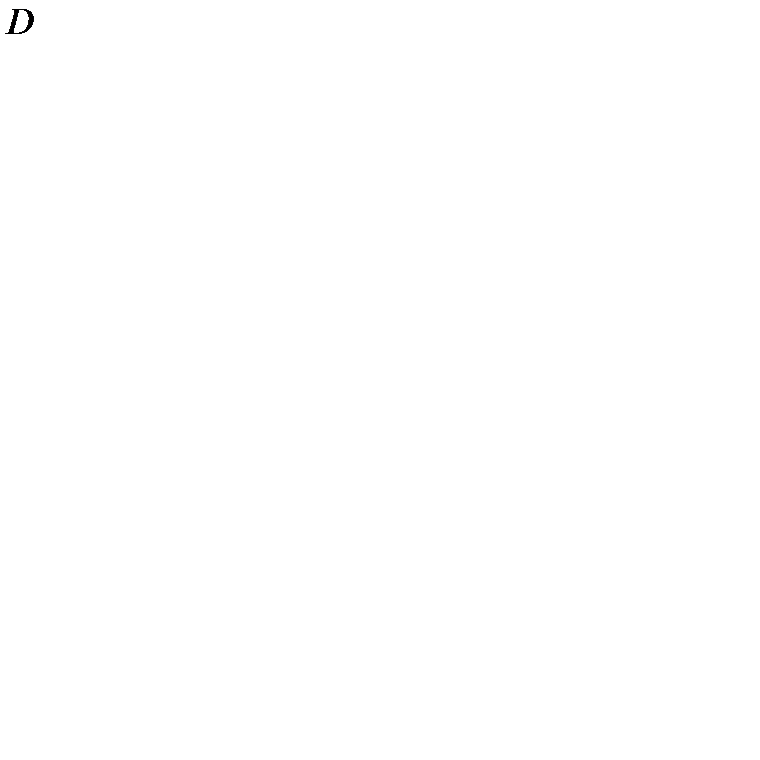 равно 6 и достигается в точках
равно 6 и достигается в точках  наименьшее значение функции
наименьшее значение функции 
 при
при  2.
2.  при
при 
 при
при  4.
4. 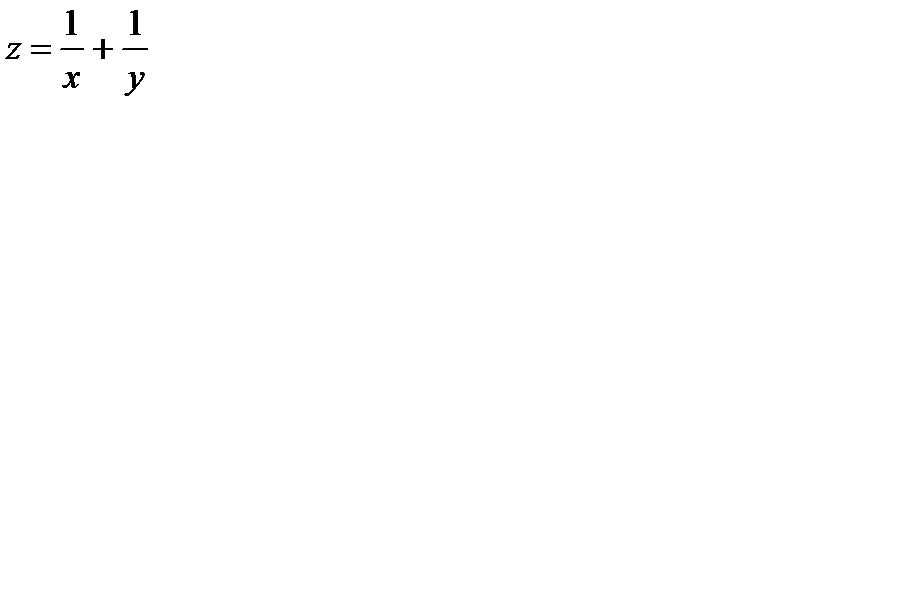 при
при 
 при
при  6.
6.  при
при 
 определить тот, площадь которого наибольшая.
определить тот, площадь которого наибольшая. если
если 
 в области
в области  и
и  .
. при
при  2.
2.  при
при 
 при
при 
 при
при 
 при
при  5.
5.  при
при 
 при
при 
 при
при  7. Равносторонний треугольник со стороной
7. Равносторонний треугольник со стороной 
 во всех точках отрезков
во всех точках отрезков  и
и 
 при
при 
 при
при 
 при
при 
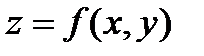 (или
(или 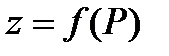 ), определенную в некоторой замкнутой области
), определенную в некоторой замкнутой области 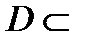
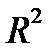 . Разобьем область
. Разобьем область 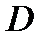 какими-нибудь линиями на
какими-нибудь линиями на 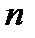 областей
областей 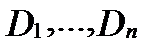 , которые могут пересекаться только по своим границам. Обозначим площадь области
, которые могут пересекаться только по своим границам. Обозначим площадь области 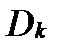 через
через 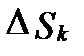 . Тогда
. Тогда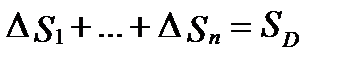 , где
, где 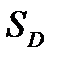 - площадь области
- площадь области 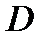 .
.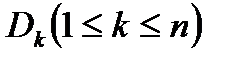 выберем произвольным образом точку
выберем произвольным образом точку 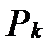 . Вычислим значение
. Вычислим значение 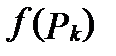 функции
функции 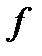 в точке
в точке 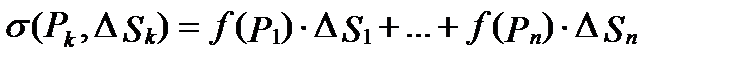 (1)
(1)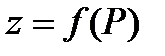 в области
в области 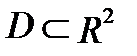 . Число
. Число 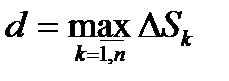 называется диаметром разбиения области
называется диаметром разбиения области 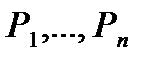 , то этот предел называется двойным интегралом от функции
, то этот предел называется двойным интегралом от функции 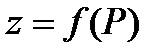 по области
по области 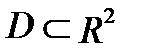 , а сама функция называется интегрируемой в области
, а сама функция называется интегрируемой в области 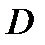 .
.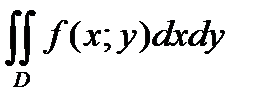 . Тогда
. Тогда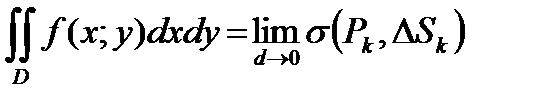 . (2)
. (2)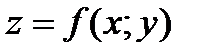 непрерывна в замкнутой области
непрерывна в замкнутой области 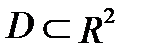 . Тогда она интегрируема на области
. Тогда она интегрируема на области 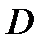 и существует ее двойной интеграл по области
и существует ее двойной интеграл по области 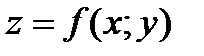 непрерывна в области
непрерывна в области 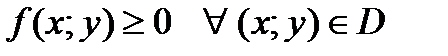 .
.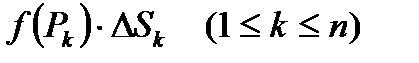 представляет собой с геометрической точки зрения объем цилиндрического тела с основанием
представляет собой с геометрической точки зрения объем цилиндрического тела с основанием 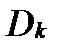 , площадь которого
, площадь которого 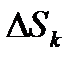 , и высотой
, и высотой 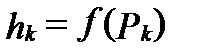 .
.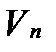 некоторого ступенчатого цилиндрического тела. Тогда предел (2) при
некоторого ступенчатого цилиндрического тела. Тогда предел (2) при 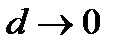 (то есть
(то есть 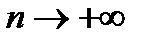 ) совпадает с объемом
) совпадает с объемом 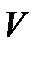 тела, ограниченного снизу областью
тела, ограниченного снизу областью 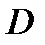 , сверху – поверхностью
, сверху – поверхностью 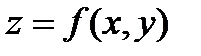 , сбоку - цилиндрической поверхностью, образующие которой параллельны оси
, сбоку - цилиндрической поверхностью, образующие которой параллельны оси 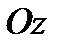 , а направляющей служит граница области
, а направляющей служит граница области 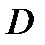 .
.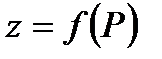 не сохраняет знак в области
не сохраняет знак в области 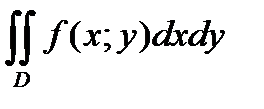 с геометрической точки зрения есть алгебраическая сумма объемов, учитываемых с «+» или «-» в зависимости от того, лежит поверхность
с геометрической точки зрения есть алгебраическая сумма объемов, учитываемых с «+» или «-» в зависимости от того, лежит поверхность 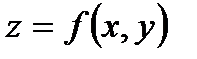 выше или ниже плоскости
выше или ниже плоскости  .
. интегрируема в области
интегрируема в области 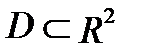 , где
, где 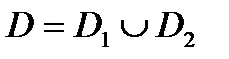 и
и 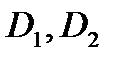 пересекаются только по своим границам. Тогда функция
пересекаются только по своим границам. Тогда функция 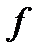 интегрируема отдельно в
интегрируема отдельно в 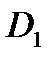 и в
и в 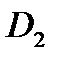 , причем справедливо равенство:
, причем справедливо равенство: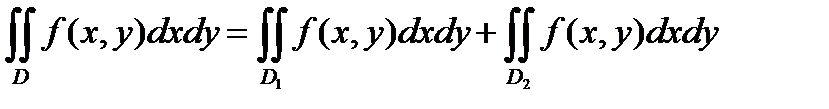 .
. интегрируемы в области
интегрируемы в области 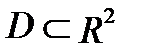 , то в
, то в 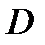 будут интегрируемы также следующие функции:
будут интегрируемы также следующие функции: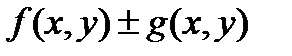 ;
;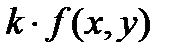 , где
, где 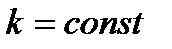 ;
;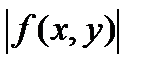 ;
;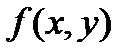
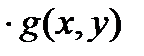 ;
;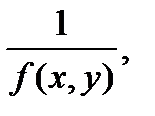 если
если 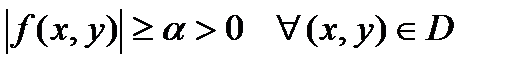 .
.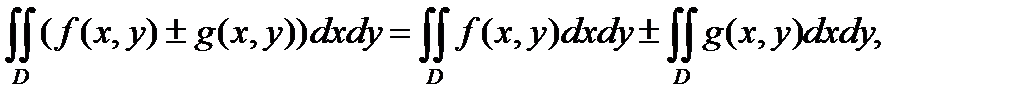
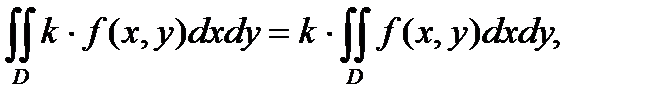
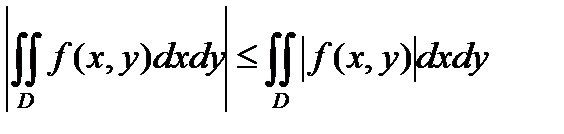 .
.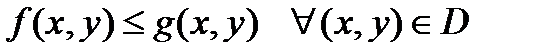 , то справедливо неравенство:
, то справедливо неравенство: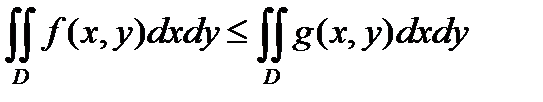 .
. и
и 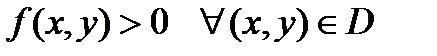 , то справедливо неравенство:
, то справедливо неравенство: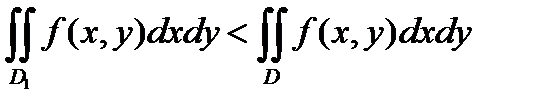 , если
, если 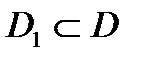 .
.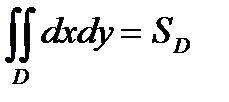 , где
, где 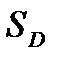 - площадь области
- площадь области 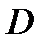 .
.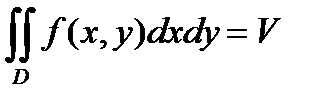 , где
, где 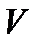 - объем тела, ограниченного снизу областью
- объем тела, ограниченного снизу областью 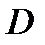 , принадлежащей плоскости
, принадлежащей плоскости 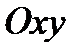 , сверху - поверхностью
, сверху - поверхностью 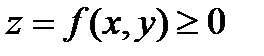 , сбоку - цилиндрической поверхностью, образующие которой параллельны оси
, сбоку - цилиндрической поверхностью, образующие которой параллельны оси 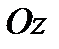 , а направляющей служит граница области
, а направляющей служит граница области 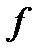 непрерывна в области
непрерывна в области 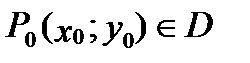 , в которой выполняется равенство:
, в которой выполняется равенство: 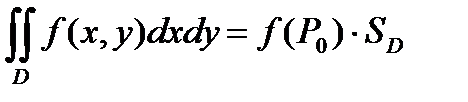 .
.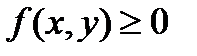
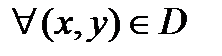 , то с геометрической точки зрения из свойства 7 заключаем: двойной интеграл от функции
, то с геометрической точки зрения из свойства 7 заключаем: двойной интеграл от функции  по области
по области  равен объему некоторого цилиндра с основанием
равен объему некоторого цилиндра с основанием 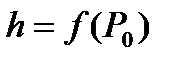 , где
, где 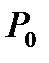 - определенная точка из
- определенная точка из  и выходящими из точек границы области
и выходящими из точек границы области 


