Математическое представление гармонии, как правило, выражается в виде определенных числовых пропорций. Древние понимали пропорцию следующим образом: «Две части или две величины не могут быть ...связаны между собой без посредства третьей....Достигается это...пропорцией (аналогией), в которой из трех чисел..., среднее так относится ко второму, как первое к среднему, а также второе к среднему, как среднее к первому» [121, с. 435]. Пропорция такого рода получила у древних название «деление в среднем и крайнем отношении», а в дальнейшем – «золотая пропорция». В приведенном высказывании Платон четко указал на «золотую пропорцию», хотя и не использовал это название. Под пропорцией здесь понимается отношение частей целого между собой и с целым; очевидна особая роль среднего пропорционального (Ф=1,618…). Важная особенность золотой пропорции заключается в том, что это результат согласования двух соотношений, поэтому необходимо иметь три элемента в отличие от отношения, где достаточно двух: да – нет, хорошо – плохо, порядок – беспорядок и т.д. Среднее пропорциональное содержит в себе «качественное обобщение, т.к. оно выражается одним числом, а не множеством» (отмечено нами. В.Ц.) [105, с. 162]. Таким образом, отдельные конкретные числа и отношения способны выражать не только количество, но и «качество». Золотое сечение является самым известным примером «качества», представленного в отношении.
Учение о золотом сечении возникло в результате тщательного исследования природы чисел. Считается, что деление отрезка в среднем и крайнем отношении впервые было осуществлено великим философом и геометром Древней Греции Пифагором (570-500 до н.э.). Возможно, по мнению Вардена [28], Пифагор позаимствовал деление отрезка в среднем и крайнем отношении у древних египтян и вавилонян. В форме алгебраического выражения это соотношение можно представить следующим образом. Отрезок единичной длины AB можно разделить на две части точкой С так, что отношение большей части (CB=x) к меньшей (AС=1-x) будет равняться отношению всего отрезка (AB=1) к его большей части (CB): СB/AC=(AC+CB)/CB, т.е. x/(1-x) =1/x. Отсюда имеем выражение:
x2 + x - 1 = 0. (1.1)
Положительным корнем этого уравнения является (-1+ 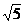 )/2, так что отношение 1/х в рассматриваемой пропорции равно иррациональному числу:
)/2, так что отношение 1/х в рассматриваемой пропорции равно иррациональному числу:
Ф= 1/х = 1,618033989...
Число 1,618… получило обозначение Ф (PHI) в честь древнегреческого зодчего Фидия (ок. 490-430 до н. э.), который использовал золотую пропорцию в создании скульптур и строительстве храмов. Об этом числе писали Поликлет (5в. до н. э.), Платон (428-348 до н. э.), Евклид (325-265 до н. э.), Витрувий (1в. до н. э.) и др. Величину 1/Ф=0,618…, обратную Ф, обозначают φ. Для реальных вычислений обычно используют Ф=1,618 и φ=0,618. Помимо алгебраического представления, величина Ф может быть вычислена с достаточной точностью по двум процедурам:
по рациональным числам,


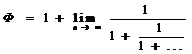
и по иррациональным числам,
Ф= 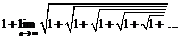
А.П. Стахов обращает внимание на то, что эти «формулы… вызывают неосознанное чувство ритма и гармонии, когда мы начинаем задумываться над бесконечной повторяемостью одних и тех же простых математических элементов» [160, с. 34].
«Золотая» точка разделяет единичный отрезок в соответствии с золотой пропорцией:
1 : 0,618 = 0,618 : 0,382 = 1,618…
«Долевое» деление единичного отрезка по золотой пропорции имеет вид:
0,382 + 0,618 = 1.
Отметим, что в первом из этих двух выражениий представлена симметрия подобия, где число 1,618 является инвариантом. Во втором выражении представлена асимметрия деления единичного отрезка. Очевидно, что структура представленных выражений не изменится при умножении их элементов на некоторое число А, имеющее любую размерность (см, сек, кал, см3 и т.п.), что имеет большое значение при анализе структуры объектов самой различной «природы».
Следующий важнейший вклад в сокровищницу Математики Гармонии был сделан в 13 веке итальянским ученым Леонардо Пизанским (1170-1240), более известным как Фибоначчи. Фибоначчи был первым крупным математиком средневековой Европы. Ученый изучал труды математиков стран ислама, по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки. В 1202 г. вышло в свет его сочинение «Liber abaci» («Трактат по арифметике»). В книге излагается множество задач. Одна из них ставится и решается следующим образом: «Сколько пар кроликов в один год от одной пары рождается? Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как 1-я пара в 1-м месяце дает потомство, удвой, и в этом месяце окажется две пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце окажется 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родится еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5 и т. д». Свое решение задачи Фибоначчи представляет так: «Мы складываем первое число со вторым, т.е. 1 и 2; и второе с третьим; и третье с четвертым; и так одно за другим, пока не сложим десятое с одиннадцатым, т.е. 144 и 233; и мы получим общее число кроликов, т.е. 377; и так можно делать по порядку до бесконечного числа месяцев». Таким образом, получилась последовательность чисел: 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т. д. Этот ряд чисел в дальнейшем получил название ряда Фибоначчи. Числа ряда Фибоначчи обычно обозначают буквой F. Обозначив число кроликов в n-ый месяц через Fn, а в следующие месяцы - Fn+1, Fn+2 и т.д., последовательность чисел ряда Фибоначчи можно представить обобщенной рекуррентной формулой:
Fn+2 = Fn + Fn+1.
В дальнейшем И. Кеплер (1571-1630) впервые установил, что Fn+1/Fn ® Ф, а Р. Симпсон (1687-1768) строго доказал, что при достаточном удалении от начала ряда  Fn+1/Fn=Ф. Отметим при этом, что при таком удалении в тройке соседних чисел имеет место и симметрия, и асимметрия. Следует добавить, что для любой числовой последовательности с начальными a>0 и b>0 при некотором удалении от начала отношение соседних чисел сходится к величине Ф. Однако наибольшей скоростью сходимости к золотой пропорции обладает последовательность, построенная по числам Фибоначчи [115].
Fn+1/Fn=Ф. Отметим при этом, что при таком удалении в тройке соседних чисел имеет место и симметрия, и асимметрия. Следует добавить, что для любой числовой последовательности с начальными a>0 и b>0 при некотором удалении от начала отношение соседних чисел сходится к величине Ф. Однако наибольшей скоростью сходимости к золотой пропорции обладает последовательность, построенная по числам Фибоначчи [115].
В 19 веке в математике вновь проявляется значительный интерес к золотому сечению. У истоков этого направления стояли два известных французских математика Ф. Люка (1842-1891) и Ж.Ф. Бине (1786-1856). Главным достижением Люка являются его исследования в области «теории чисел Фибоначчи». Он впервые ввел название «числа Фибоначчи». Кроме того, он ввел так называемые «обобщенные числа Фибоначчи», которые формируются по тем же правилам, что и числа Фибоначчи, но при других начальных условиях. Он показал, что среди «обобщенных чисел Фибоначчи», кроме чисел Фибоначчи, особую роль играет еще одна числовая последовательность, названная впоследствии рядом чисел Люка Ln: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76…
Бине является автором знаменитых формул Бине:
Fn=(Фn-(-1)nФ-n)/ 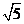 ,
,
Ln=Фn+(-1)nФ-n .
В этих формулах целые числа рядов Фибоначчи Fn и Люка Ln получены с использованием иррациональных чисел Ф и 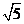 . Ряд Фибоначчи Fn: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… An-2, An-1, An,…и ряд Люка Ln: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,… An-2, An-1, An,… можно представить обобщенным уравнением:
. Ряд Фибоначчи Fn: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… An-2, An-1, An,…и ряд Люка Ln: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,… An-2, An-1, An,… можно представить обобщенным уравнением:
An-1=An-1+An-2.
Золотое число Ф=1,618… можно представить как фрактальную функцию от рядов Фибоначчи и Люка:
Ф = (Ln+1+Fn+1 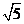 )/(Ln+Fn
)/(Ln+Fn 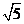 ) = (Ln- Fn
) = (Ln- Fn 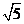 )/(-Ln+1+Fn+1
)/(-Ln+1+Fn+1 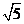 ),
),
где n = 1, 2, 3, 4,…..¥.
Отметим, формулы Бине являются как бы связующим звеном между целыми и иррациональными числами. На основании формул Бине украинскими учеными А.П. Стаховым и И.С. Ткаченко [156] были открыты гиперболические функции Фибоначчи и Люка. Основу нового класса гиперболических функций представляет анализ формул Бине и Люка. В отличие от классических гиперболических функций, основанием которых является число е=2,718 (основание натуральных логарифмов), основанием нового класса является число Ф=1,618:
sFs(x) = (Ф2х-Ф-2х)/ 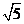 ,
,
cFs(x)= (Ф2х+Ф-2х)/ 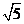 .
.
Эти функции имеют прямое отношение к теоретическому естествознанию. Как показано в исследованиях О.Я. Боднара [20, 21], гиперболические функции Фибоначчи лежат в основе геометрической теории ботанического явления филотаксиса, который известен в науке еще со времен Кеплера.
Нами отмечена [201] полная аналогия между геометрической прогрессией золотых чисел f1=Ф0, f2=Ф1, f3=Ф2, f4=Ф3,..., fn=Фn-1, fn+1=Фn, fn+2=Фn+1,…и арифметическим рядом, построенным по рекуррентной формуле fn+2=fn+fn+1…, где первыми членами ряда являются числа Ф0 и Ф1. «Геометрический» и «арифметический» ряды «золотых» чисел обладают замечательным свойством: числа этих рядов, начиная с первого и дальше, полностью совпадают. Отметим, что подобное совпадение имеет место только для арифметической и геометрической последовательностей с начальными членами Ф0=1 и Ф1=1,618. Аналогично можно представить нисходящую прогрессию Ф0, Ф-1, Ф-2, Ф-3,..., Ф-(n-1), Ф-n, Ф-(n+1) и т. д. и нисходящий арифметический ряд золотых чисел fn-2 = fn - fn-1,.., в которых свойство равенства также соблюдается. Естественно, эти отношения сохраняются и при умножении восходящих и нисходящих «золотых» рядов на любую величину A как безразмерную, так и имеющую какую-либо размерность (сек, см, эрг, см3 и т. д.). Любые три соседних числа этих последовательностей заключают в себе симметрию подобия и асимметрию «противоположностей». Отметим, восходящие и нисходящие ряды золотых чисел отражают реальные биофизические и биохимические процессы (см. разделы 2.2 и 2.3).
В 20 веке были получены новые крупные результаты, изменившие сложившиеся представления в современной математике.
Американский математик Дж. Бергман [243] в 12 лет предложил необычный способ позиционного представления чисел:
A=  ,
,
где А – действительное число, ai – двоичная цифра {0,1} i-разряда, i = 0, 1, 2, 3,…, Фi – вес – i-разряда, Ф=1,618 – основание счисления. Основная отличительная особенность «системы Бергмана» состояла в том, что ее основанием является золотое число Ф. С помощью иррационального числа Ф можно представить все действительные числа. Это означает, что любое натуральное число может быть представлено в виде конечного числа степеней Ф. Система Бергмана переворачивает классическое представление о позиционных системах счисления, исторически сложившееся представление о связи рациональных и иррациональных чисел. До открытия Бергмана считалось, что основанием позиционной системы счисления может быть только целое число (10 – для десятичной системы, 2 – для двоичной, 60 – для Вавилонской 60-ричной системы). В «системе Бергмана» основанием системы, т. е. началом исчисления явлется иррациональное число Ф = (1+ 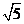 )/2, с помощью которого можно представить все действительные числа, включая натуральные и иррациональные.
)/2, с помощью которого можно представить все действительные числа, включая натуральные и иррациональные.
В последней четверти 20 века А.П. Стаховым было сделано важное открытие [153]. Объектом открытия были обобщенные золотые р-пропорции, где классическое золотое сечение является лишь частным случаем. Геометрическая интерпретация рекуррентного соотношения для р-чисел Фибоначчи может быть получена, если мы разделим отрезок АВ точкой С в таком отношении, чтобы AB/CB=x, а CB/ACp =xp. Значение искомого отношения АВ/СВ сводится к решению алгебраического уравнения:
xp+1+ xp - 1 = 0. (1.2)
Ниже приведены приближенные значения золотых р-пропорций, соответствующие начальным значениям р:
| p
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
|
| Фp
| 2
| 1,618
| 1,465
| 1,380
| 1,324
| 1,285
| 1,255
| 1,232
| 1,213
|
При p=1 уравнение принимает классический «золотой» вид:
x2 + x - 1 = 0.
Корнем данного уравнения является число 1/Ф=(-1+ 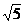 )/2=0,618. По аналогии с классической золотой пропорцией положительный р-корень уравнения называется обобщенной золотой пропорцией или р-пропорцией, а соответствующее деление отрезка - золотым р-сечением.
)/2=0,618. По аналогии с классической золотой пропорцией положительный р-корень уравнения называется обобщенной золотой пропорцией или р-пропорцией, а соответствующее деление отрезка - золотым р-сечением.
Значительный интерес к золотым р-сечениям был проявлен в философской науке. Э.М. Сороко возвел их в ранг «закона структурной гармонии систем», который он формулирует следующим образом: «Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоническое строение, стационарный режим существования, структурно-функциональную ...устойчивость» [151]. Эти золотые сечения по отношению к нормированию противоположностей к единице образуют своего рода интерференционную решетку («узлы») - 0,500+0,500; 0,382+0,618; 0,318+0,682;0,276+0,724 и т.д. Их разделяют «пучности» - 0,430+0,570; 0,346+0,654; 0,295+0,705 и т. д. «Узлы» представляют зоны согласованности, устойчивости, а, следовательно, и гармонии самоорганизующихся систем, а «пучности» - зоны неустойчивости и дисгармонии. В качестве обобщения Сороко представил следующий вывод: «Структурная гармония систем природы, т. е. гармония их внутреннего строения, подчиняется четкому математическому закону».
В конце 20 и в начале 21 века аргентинский математик В. Шпинагель [325], французский математик и инженер М. Газале [255], американский математик Д. Каппраф [274] и российский инженер А. Татаренко (167) независимо друг от друга пришли к новому классу математических констант, названных «металлическими пропорциями». Эти пропорции заключены в уравнении
x2 -lx-1 = 0, (1.3)
корнями которого являются
Фλ=  /2,
/2,
где λ>0 – любое действительное число. Формула задает бесконечное количество новых математических констант. «Металлические» пропорции или «золотые λ-пропорции» обладают рядом замечательных свойств. Заметим, что при λ=1 «металлическая пропорция» сводится к классической золотой пропорции (1.1). А.П. Стахов пришел к выводу, что «в современной Математике Гармонии успешно развиваются две обобщенные теории золотого сечения: первая основана на «золотых» р-пропорциях, вторая на «металлических» пропорциях» [164]. Классическая золотая пропорция (1.1) является частным случаем пропорций (1.2) и (1.3).
Итак, в основе Математики Гармонии лежит «золотая» парадигма. Ее суть состоит в том что, «начиная какое-либо фундаментальное исследование, мы должны взять за основу «золотую» парадигму, то есть Платоновы тела, золотое сечение, числа Фибоначчи и их обобщения – золотое р-сечение, «металлические» пропорции и вообще всю Математику Гармонии» [205]. Все представленные выше математические соотношения, где отражено «присутствие» числа Ф=1,618, связаны с фундаментальными проблемами современной науки; они представляют Математику Гармонии во многих явлениях окружающего нас мира. По мнению А.П. Стахова, «Интерес к числам Фибоначчи, золотому сечению и проблемам гармонии систем, возникший в современной науке, является подтверждением «естественного» хода развития современной науки, которая приближается к раскрытию законов гармонии, созданию новой научной картины мира, основанной на идеях гармонии, симметрии и золотого сечения (отмечено нами. В.Ц.). Это приведет к восстановлению и углублению связей между Наукой и Искусством как двух взаимно дополняющих методов раскрытия и отображения объективной гармонии Мироздания» [158, с. 212].



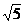 )/2, так что отношение 1/х в рассматриваемой пропорции равно иррациональному числу:
)/2, так что отношение 1/х в рассматриваемой пропорции равно иррациональному числу:
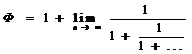
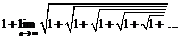
 Fn+1/Fn=Ф. Отметим при этом, что при таком удалении в тройке соседних чисел имеет место и симметрия, и асимметрия. Следует добавить, что для любой числовой последовательности с начальными a>0 и b>0 при некотором удалении от начала отношение соседних чисел сходится к величине Ф. Однако наибольшей скоростью сходимости к золотой пропорции обладает последовательность, построенная по числам Фибоначчи [115].
Fn+1/Fn=Ф. Отметим при этом, что при таком удалении в тройке соседних чисел имеет место и симметрия, и асимметрия. Следует добавить, что для любой числовой последовательности с начальными a>0 и b>0 при некотором удалении от начала отношение соседних чисел сходится к величине Ф. Однако наибольшей скоростью сходимости к золотой пропорции обладает последовательность, построенная по числам Фибоначчи [115].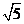 ,
, ,
, /2,
/2,

