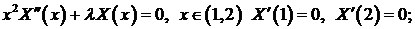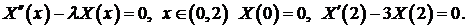Задача Штурма – Лиувилля
А). Постановка задачи
Применение метода Фурье к решению задач математической физики (уравнений любого из трех типов) приводит к краевым задачам для обыкновенного линейного дифференциального однородного уравнения второго порядка, содержащего параметр. С нулевыми граничными условиями такие задачи, как правило, при любом значении параметра имеют тождественно равное нулю решение. Но при некоторых значениях параметра возможны и нетривиальные решения. В этих задачах требуется найти такие значения параметра, при которых существует отличное от нуля решение однородного уравнения, удовлетворяющее на концах отрезка однородным граничным условиям.
Сформулируем задачу Штурма-Лиувилля (Ш. – Л.):
Найти значения параметра  при которых уравнение
при которых уравнение
 (1)
(1)
имеет нетривиальные решения 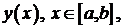 удовлетворяющие однородным краевым условиям
удовлетворяющие однородным краевым условиям
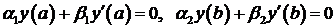 , (2)
, (2)
и найти эти решения.
Б). Нахождение собственных значений и собственных функций.
Пусть выполнены условия регулярности: 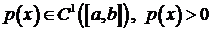 при
при 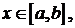
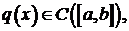

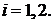 Предполагается, что решение задачи
Предполагается, что решение задачи 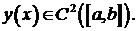 Значение параметра
Значение параметра  при котором существует нетривиальное решение задачи Ш. – Л., называется собственным значением, а соответствующее нетривиальное решение
при котором существует нетривиальное решение задачи Ш. – Л., называется собственным значением, а соответствующее нетривиальное решение 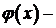 собственной функцией.
собственной функцией.
При сделанных предположениях существует фундаментальная система решений 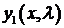 ,
, 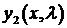 уравнения (1). Общее решение этого уравнения имеет вид
уравнения (1). Общее решение этого уравнения имеет вид
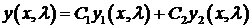 (3)
(3)
Здесь  – произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть
– произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть 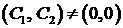 .
.
Подставим функцию (3) в краевые условия (2):
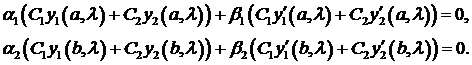
Получим алгебраическую линейную однородную систему относительно 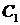 и
и 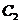 :
:
 (4)
(4)
Однородная система имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю:
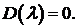 (5)
(5)
Значит, те значения 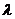 , при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни
, при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни  этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде
этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде 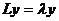 , то совокупность собственных значений – это спектр линейного оператора
, то совокупность собственных значений – это спектр линейного оператора  .
.
Пусть 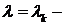 корень уравнения (5), тогда имеем ненулевое решение системы (4)
корень уравнения (5), тогда имеем ненулевое решение системы (4)  ,
, 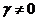 ,
, 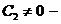 свободное неизвестное. Соответствующие собственные функции
свободное неизвестное. Соответствующие собственные функции 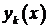 определяем по формуле (3) при
определяем по формуле (3) при  :
:

Собственные (спектральные) функции определены с точностью до постоянного множителя 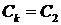 .
.
В) Свойства собственных значений и собственных функций.
Свойство 1. Краевая задача (1) – (2) имеет счетное множество собственных значений и все они вещественны. Если собственные значения рассматривать в порядке возрастания:  , то
, то 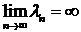 .
.
Свойство 2. Все собственные значения задачи Штурма – Лиувилля (1) – (2) простые, то есть каждому собственному значению соответствует одна собственная функция.
Свойство 3. Собственные функции, соответствующие различным собственным значениям, ортогональны на 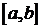 , то есть удовлетворяют равенству
, то есть удовлетворяют равенству
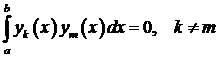 .
.
Свойство 4. Если краевые условия таковы, что
 ,
,
то все собственные числа задачи (1) – (2) неотрицательны.
Свойство 5. (Теорема Стеклова). Пусть функция  и удовлетворяет на концах отрезка условиям (2). Тогда
и удовлетворяет на концах отрезка условиям (2). Тогда 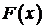 разлагается в равномерно и абсолютно сходящийся при
разлагается в равномерно и абсолютно сходящийся при 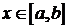 ряд Фурье по собственным функциям краевой задачи (1) – (2)
ряд Фурье по собственным функциям краевой задачи (1) – (2)
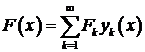 ,
,
где 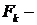 коэффициенты Фурье, определяемые по формуле:
коэффициенты Фурье, определяемые по формуле:

Задача 1. Найти собственные значения и собственные функции задачи Ш. – Л.
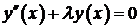 ,
, 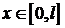
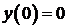 ,
, 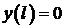 .
.
Решение. Ищем решение уравнения в виде  . Запишем характеристическое уравнение:
. Запишем характеристическое уравнение: 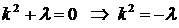 .
.
1. Пусть 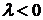 , тогда корни характеристического уравнения действительны и различны:
, тогда корни характеристического уравнения действительны и различны:  . Фундаментальная система решений
. Фундаментальная система решений 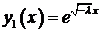 ,
, 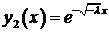 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид:
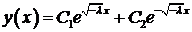 ,
,
где 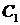 и
и  произвольные постоянные. Используя заданные краевые условия, получим систему для определения
произвольные постоянные. Используя заданные краевые условия, получим систему для определения 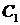 ,
, 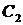 :
:
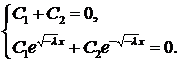
Определитель этой системы 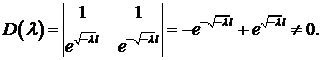 Значит, система имеет единственное решение
Значит, система имеет единственное решение 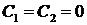 . Поэтому в случае
. Поэтому в случае 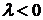 данная задача собственных значений и собственных функций не имеет.
данная задача собственных значений и собственных функций не имеет.
2. Пусть 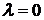 . Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений
. Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений 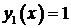 ,
,  . Общее решение уравнения – линейная функция
. Общее решение уравнения – линейная функция 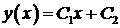 . Подставляя краевые условия, получим
. Подставляя краевые условия, получим 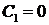 ,
, 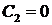 . Значит,
. Значит, 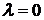 не является собственным значением рассматриваемой задачи Ш. – Л.
не является собственным значением рассматриваемой задачи Ш. – Л.
3. Пусть 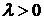 . Корни характеристического уравнения мнимые:
. Корни характеристического уравнения мнимые: 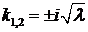 . Фундаментальная система решений
. Фундаментальная система решений 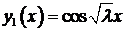 ,
,  . Общее решение уравнения
. Общее решение уравнения
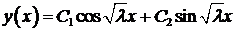 .
.
Определим 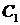 ,
, 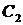 из краевых условий. При
из краевых условий. При  (на левом конце)
(на левом конце) 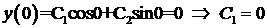 . При
. При 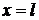 (на правом конце) получаем
(на правом конце) получаем 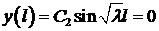 . Нас интересует нетривиальное решение, то есть
. Нас интересует нетривиальное решение, то есть 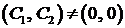 , поэтому
, поэтому 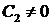 . Тогда должен быть равен нулю второй множитель
. Тогда должен быть равен нулю второй множитель

Итак, 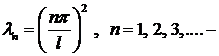 собственные значения, тогда решения
собственные значения, тогда решения 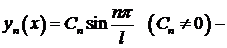 собственные функции данной задачи Ш. – Л. ●
собственные функции данной задачи Ш. – Л. ●
Замечание. Иногда в уравнении 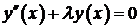 удобнее вместо
удобнее вместо 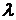 брать
брать 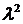 . Тогдасобственные значения задачи 1 можно записать в виде
. Тогдасобственные значения задачи 1 можно записать в виде 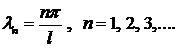
Задача 2. Найти собственные значения и собственные функции задачи Штурма – Лиувилля
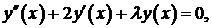
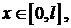
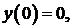

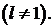
Решение. Составим характеристическое уравнение 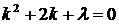 и найдем его корни
и найдем его корни 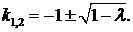
1. Пусть 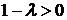 , то есть
, то есть  . Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
. Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
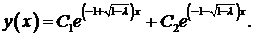
Краевые условия приводят к системе для определения 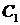 ,
, 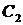 :
:
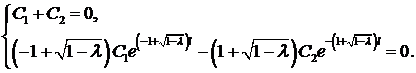
Определитель этой системы

Тривиальное решение является единственным. Значит, задача в случае 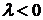 не имеет собственных значений и собственных функций.
не имеет собственных значений и собственных функций.
2. Пусть 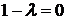 . У характеристического уравнения кратные корни
. У характеристического уравнения кратные корни 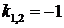 . Общее решение
. Общее решение 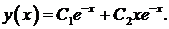 Из краевых условий получим систему
Из краевых условий получим систему

Отсюда 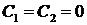 , так как по условию
, так как по условию 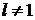 . Значит,
. Значит, 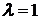 не является собственным значением.
не является собственным значением.
3. Пусть 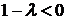 , то есть
, то есть 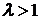 . Характеристическое уравнение имеет комплексно сопряженные корни
. Характеристическое уравнение имеет комплексно сопряженные корни 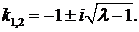 Общее решение уравнения
Общее решение уравнения
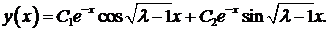
Из краевых условий получаем

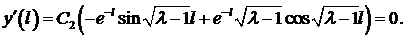
Случай 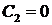 дает тривиальное решение, то есть нас не интересует. Выясним, при каком значении
дает тривиальное решение, то есть нас не интересует. Выясним, при каком значении 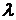 может обращаться в нуль выражение в скобках
может обращаться в нуль выражение в скобках
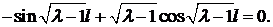
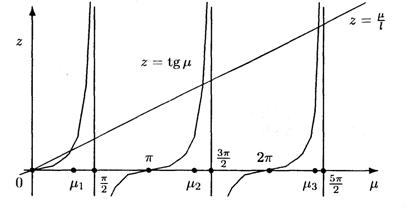 Приходим к уравнению
Приходим к уравнению 
Обозначим  , тогда уравнение для определения собственных значений запишется так:
, тогда уравнение для определения собственных значений запишется так:

Это трансцендентное уравнение, которое можно решить, например, графически. Обозначим последовательные положительные корни этого уравнения  Тогда
Тогда  и
и 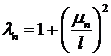 ,
,  собственные значения, а
собственные значения, а 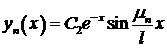 ,
, 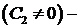 собственные функции этой задачи. ●
собственные функции этой задачи. ●
Задача 3. Найти собственные значения и собственные функции задачи Штурма – Лиувилля:
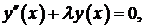
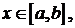
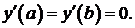
Решение. Запишем характеристическое уравнение 
1. Пусть  Тогда корни характеристического уравнения действительны и различны:
Тогда корни характеристического уравнения действительны и различны: 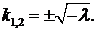 Общее решение уравнения
Общее решение уравнения
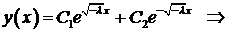
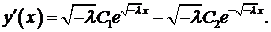
Краевые условия приводят к системе
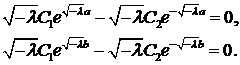
Определитель этой системы
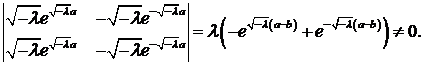
Система имеет единственное решение 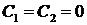 , поэтому в случае
, поэтому в случае 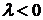 задача Ш. – Л. не имеет собственных значений и собственных функций.
задача Ш. – Л. не имеет собственных значений и собственных функций.
2. Пусть 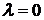 . Корни характеристического уравнения
. Корни характеристического уравнения 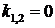 . Тогда
. Тогда

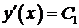 .
.
Из краевых условий находим 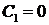 , тогда решение имеет вид
, тогда решение имеет вид 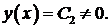 Таким образом,
Таким образом,  собственное значение,
собственное значение, 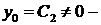 собственная функция рассматриваемой задачи Ш. – Л.
собственная функция рассматриваемой задачи Ш. – Л.
3. Пусть 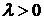 . Корни характеристического уравнения
. Корни характеристического уравнения 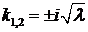 . Тогда
. Тогда

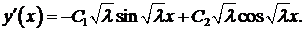
Вычислим значения производной на концах отрезка
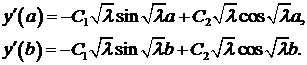
Используя краевые условия, получим систему для 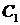 и
и 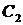 :
:

Определитель системы

Найдем те значения 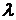 , при которых определитель равен нулю.
, при которых определитель равен нулю.
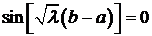

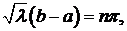
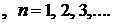 .
.
Собственные значения задачи 
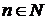 . Подставляя найденные
. Подставляя найденные 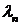 в первое (например) уравнение системы, находим
в первое (например) уравнение системы, находим
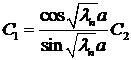 .
.
Из общего решения получаем собственные функции
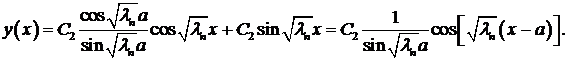
Итак, рассматриваемая задача Ш. – Л. имеет собственные значения 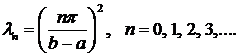 (подключили сюда
(подключили сюда 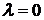 ) и собственные функции
) и собственные функции
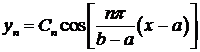 ,
, 
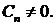
В частности, если  , собственные значения и собственные функции выглядят так:
, собственные значения и собственные функции выглядят так:
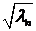 :
: 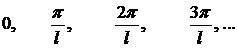
 :
: 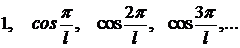 ●
●
Задачи для самостоятельного решения
- Показать, что
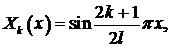
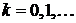 суть собственные функции задачи Штурма – Лиувилля:
суть собственные функции задачи Штурма – Лиувилля:
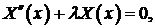
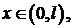
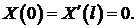
- Убедиться, что
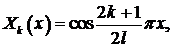
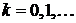 – собственные функции задачи Штурма –Лиувилля:
– собственные функции задачи Штурма –Лиувилля:
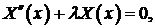

- Показать, что
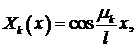
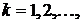 где
где 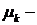 положительные корни трансцендентного уравнения
положительные корни трансцендентного уравнения  являются собственными функциями задачи Штурма-Лиувилля:
являются собственными функциями задачи Штурма-Лиувилля:
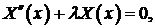
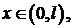

- Решить следующие задачи Штурма-Лиувилля:
a) 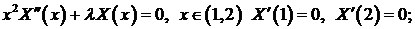
b) 
c) 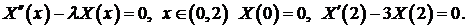



 при которых уравнение
при которых уравнение (1)
(1)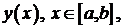 удовлетворяющие однородным краевым условиям
удовлетворяющие однородным краевым условиям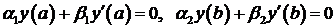 , (2)
, (2)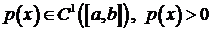 при
при 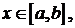
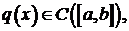

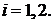 Предполагается, что решение задачи
Предполагается, что решение задачи 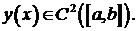 Значение параметра
Значение параметра 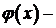 собственной функцией.
собственной функцией.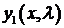 ,
, 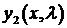 уравнения (1). Общее решение этого уравнения имеет вид
уравнения (1). Общее решение этого уравнения имеет вид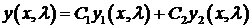 (3)
(3) – произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть
– произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть 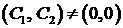 .
.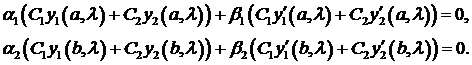
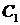 и
и 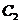 :
: (4)
(4)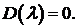 (5)
(5)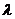 , при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни
, при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни  этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде
этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде 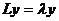 , то совокупность собственных значений – это спектр линейного оператора
, то совокупность собственных значений – это спектр линейного оператора  .
.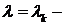 корень уравнения (5), тогда имеем ненулевое решение системы (4)
корень уравнения (5), тогда имеем ненулевое решение системы (4)  ,
, 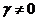 ,
, 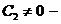 свободное неизвестное. Соответствующие собственные функции
свободное неизвестное. Соответствующие собственные функции 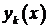 определяем по формуле (3) при
определяем по формуле (3) при  :
:
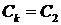 .
. , то
, то 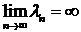 .
.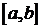 , то есть удовлетворяют равенству
, то есть удовлетворяют равенству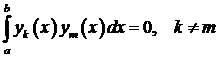 .
. ,
, и удовлетворяет на концах отрезка условиям (2). Тогда
и удовлетворяет на концах отрезка условиям (2). Тогда 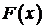 разлагается в равномерно и абсолютно сходящийся при
разлагается в равномерно и абсолютно сходящийся при 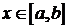 ряд Фурье по собственным функциям краевой задачи (1) – (2)
ряд Фурье по собственным функциям краевой задачи (1) – (2)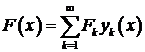 ,
,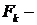 коэффициенты Фурье, определяемые по формуле:
коэффициенты Фурье, определяемые по формуле:
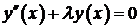 ,
, 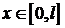
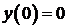 ,
, 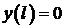 .
. . Запишем характеристическое уравнение:
. Запишем характеристическое уравнение: 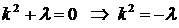 .
.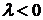 , тогда корни характеристического уравнения действительны и различны:
, тогда корни характеристического уравнения действительны и различны:  . Фундаментальная система решений
. Фундаментальная система решений 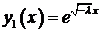 ,
, 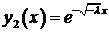 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид: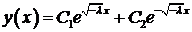 ,
, произвольные постоянные. Используя заданные краевые условия, получим систему для определения
произвольные постоянные. Используя заданные краевые условия, получим систему для определения 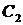 :
: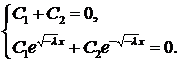
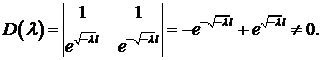 Значит, система имеет единственное решение
Значит, система имеет единственное решение 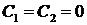 . Поэтому в случае
. Поэтому в случае 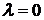 . Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений
. Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений 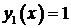 ,
,  . Общее решение уравнения – линейная функция
. Общее решение уравнения – линейная функция 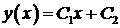 . Подставляя краевые условия, получим
. Подставляя краевые условия, получим 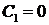 ,
, 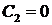 . Значит,
. Значит, 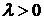 . Корни характеристического уравнения мнимые:
. Корни характеристического уравнения мнимые: 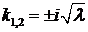 . Фундаментальная система решений
. Фундаментальная система решений 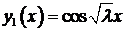 ,
,  . Общее решение уравнения
. Общее решение уравнения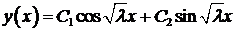 .
. (на левом конце)
(на левом конце) 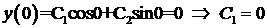 . При
. При 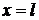 (на правом конце) получаем
(на правом конце) получаем 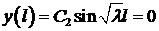 . Нас интересует нетривиальное решение, то есть
. Нас интересует нетривиальное решение, то есть 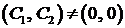 , поэтому
, поэтому 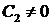 . Тогда должен быть равен нулю второй множитель
. Тогда должен быть равен нулю второй множитель
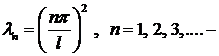 собственные значения, тогда решения
собственные значения, тогда решения 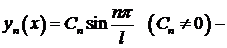 собственные функции данной задачи Ш. – Л. ●
собственные функции данной задачи Ш. – Л. ●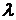 брать
брать 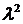 . Тогдасобственные значения задачи 1 можно записать в виде
. Тогдасобственные значения задачи 1 можно записать в виде 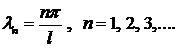
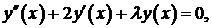
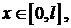
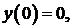

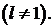
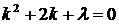 и найдем его корни
и найдем его корни 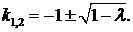
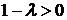 , то есть
, то есть  . Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
. Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид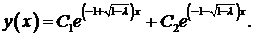
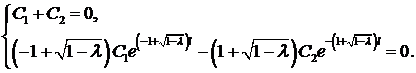

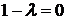 . У характеристического уравнения кратные корни
. У характеристического уравнения кратные корни 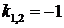 . Общее решение
. Общее решение 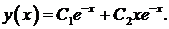 Из краевых условий получим систему
Из краевых условий получим систему
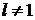 . Значит,
. Значит, 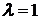 не является собственным значением.
не является собственным значением.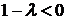 , то есть
, то есть 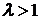 . Характеристическое уравнение имеет комплексно сопряженные корни
. Характеристическое уравнение имеет комплексно сопряженные корни 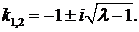 Общее решение уравнения
Общее решение уравнения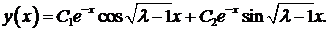

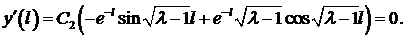
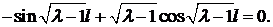
 Приходим к уравнению
Приходим к уравнению 
 , тогда уравнение для определения собственных значений запишется так:
, тогда уравнение для определения собственных значений запишется так:
 Тогда
Тогда  и
и 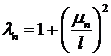 ,
,  собственные значения, а
собственные значения, а 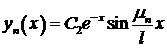 ,
, 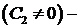 собственные функции этой задачи. ●
собственные функции этой задачи. ●

 Тогда корни характеристического уравнения действительны и различны:
Тогда корни характеристического уравнения действительны и различны: 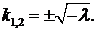 Общее решение уравнения
Общее решение уравнения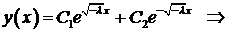
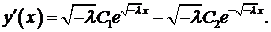
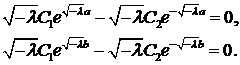
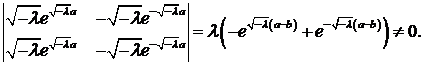
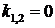 . Тогда
. Тогда
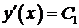 .
.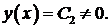 Таким образом,
Таким образом,  собственное значение,
собственное значение, 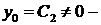 собственная функция рассматриваемой задачи Ш. – Л.
собственная функция рассматриваемой задачи Ш. – Л.
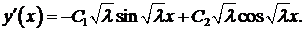
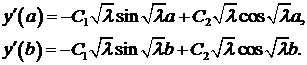


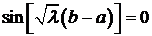

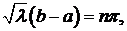
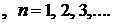 .
.
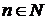 . Подставляя найденные
. Подставляя найденные 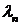 в первое (например) уравнение системы, находим
в первое (например) уравнение системы, находим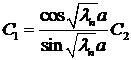 .
.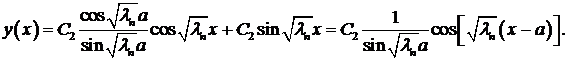
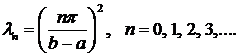 (подключили сюда
(подключили сюда 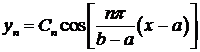 ,
, 
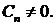
 , собственные значения и собственные функции выглядят так:
, собственные значения и собственные функции выглядят так: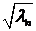 :
: 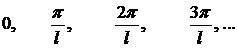
 :
: 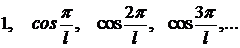 ●
●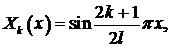
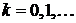 суть собственные функции задачи Штурма – Лиувилля:
суть собственные функции задачи Штурма – Лиувилля: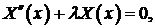
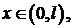
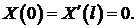
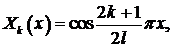

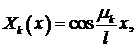
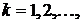 где
где 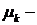 положительные корни трансцендентного уравнения
положительные корни трансцендентного уравнения  являются собственными функциями задачи Штурма-Лиувилля:
являются собственными функциями задачи Штурма-Лиувилля: