Рассмотрим задачу о свободных колебаниях бесконечной струны при заданных начальных условиях (задачу Коши):


 (1)
(1)
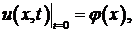

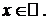 (2)
(2)
Приведем уравнение 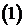 к каноническому виду. Уравнение характеристик
к каноническому виду. Уравнение характеристик  распадается на два уравнения:
распадается на два уравнения:  и
и 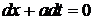 . Общие интегралы этих уравнений суть семейства прямых
. Общие интегралы этих уравнений суть семейства прямых 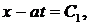
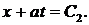 Вводим новые переменные
Вводим новые переменные 
 и пересчитываем производные:
и пересчитываем производные:
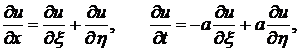

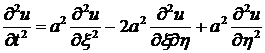
После подстановки в исходное уравнение 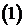 и приведения подобных членов получаем канонический вид
и приведения подобных членов получаем канонический вид  Интегрирование уравнение
Интегрирование уравнение  по
по  при фиксированном
при фиксированном  даёт общий интеграл в виде
даёт общий интеграл в виде  . Здесь
. Здесь  произвольная функция. Повторно интегрируем по
произвольная функция. Повторно интегрируем по  при фиксированном
при фиксированном  :
:
 .
.
Здесь 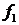 и
и  произвольные функции. Возвращаясь к старым переменным, получаем, что общим решением уравнения
произвольные функции. Возвращаясь к старым переменным, получаем, что общим решением уравнения 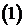 является функция
является функция
 (3)
(3)
Вид функций 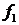 и
и 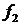 определяется из начальных условий
определяется из начальных условий 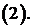
Подставим в общее решение (3)  . В силу первого начального условия
. В силу первого начального условия 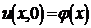 получаем
получаем
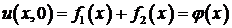 .
.
Чтобы воспользоваться вторым начальным условием, продифференцируем функцию  по переменной
по переменной 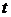 :
:

В силу условия  получаем
получаем
 .
. 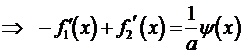 .
.
Проинтегрируем полученное соотношение

Здесь  фиксированное значение независимой переменной
фиксированное значение независимой переменной 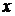 ,
, 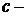 произвольная постоянная.
произвольная постоянная.
Таким образом, вид произвольных функций 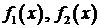 определяется из системы уравнений
определяется из системы уравнений
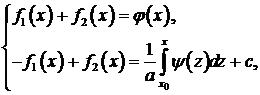



Осталось вспомнить, что у функции 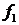 аргументом служит
аргументом служит 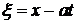 , а функция
, а функция 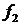 зависит от аргумента
зависит от аргумента  , и подставить найденные функции в представление
, и подставить найденные функции в представление 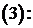
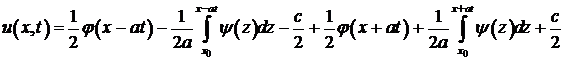
Замечая, что 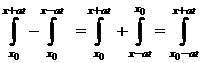 , получим окончательно
, получим окончательно
 (4)
(4)
Формула  носит название формулы Даламбера.
носит название формулы Даламбера.
Задача 1. Найти решение уравнения
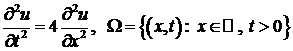 ,
,
удовлетворяющее условиям

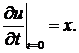
Решение. Воспользуемся формулой Даламбера. У нас 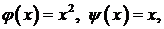
 , тогда
, тогда 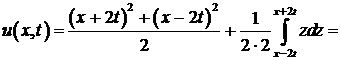
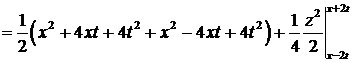 .
.
Окончательно получаем 
Легко проверить, что полученная функция  действительно есть решение задачи Коши, т.е. удовлетворяет и уравнению, и начальным условиям. ●
действительно есть решение задачи Коши, т.е. удовлетворяет и уравнению, и начальным условиям. ●
Задача 2. Найти решение уравнения
 (5)
(5)
удовлетворяющее начальным условиям
 (6)
(6)
Решение. Составим уравнение характеристик
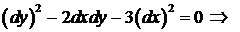
 .
.
Оно распадается на два уравнения:  и
и 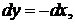 общие интегралы которых удобно записать в виде:
общие интегралы которых удобно записать в виде:  . Вводим новые переменные
. Вводим новые переменные 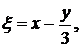
 и пересчитываем производные функции
и пересчитываем производные функции  :
:
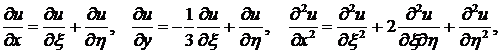
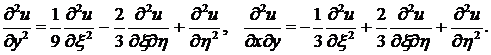
Уравнение приводится к каноническому виду  Общее его решение, как показано выше, представляется в виде
Общее его решение, как показано выше, представляется в виде 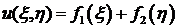 , где
, где  – произвольные функции. Значит, для исходного уравнения
– произвольные функции. Значит, для исходного уравнения
 (7)
(7)
Для определения функций  следует использовать начальные условия.
следует использовать начальные условия.
При 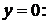
 .
.
Замечание. Теперь очевидно преимущество записи 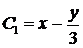 , т.е.
, т.е.  – при
– при 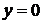 получаем
получаем  . Если бы
. Если бы  , то
, то 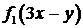 и при
и при 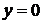 получили бы
получили бы  .
.
Дифференцируем функцию  по
по 
 .
.
При 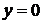 :
: 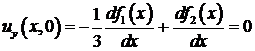

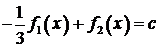 .
.
Из системы уравнений 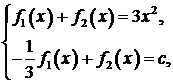 находим вид функций
находим вид функций 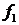 и
и 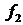 :
:
 ,
, 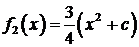 .
.
Осталось 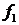 и
и 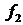 подставить в общее решение
подставить в общее решение 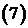 . При этом следует помнить, что у функция
. При этом следует помнить, что у функция 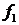 зависит от аргумента
зависит от аргумента 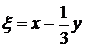 , а у функции
, а у функции 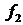 – от аргумента
– от аргумента  . Получаем:
. Получаем:
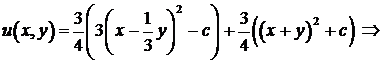
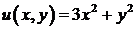 .
.
Легко убедиться, что эта функция действительно есть решение задачи Коши, т.е. удовлетворяет и уравнению, и начальным условиям. ●
Задача 3. Найти решение уравнения

удовлетворяющее начальным условиям 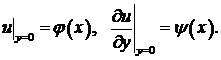
Рассмотреть частный случай 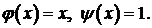
Решение. Уравнение характеристик  распадается на два уравнения:
распадается на два уравнения: 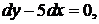 и
и  . Общие интегралы удобнее записать в виде:
. Общие интегралы удобнее записать в виде: 
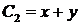 . Новые переменные
. Новые переменные  . Дифференцируем сложную функцию
. Дифференцируем сложную функцию 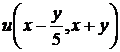 :
:

Уравнение в результате замены приводится к каноническому виду

Перепишем уравнение в виде  и найдем его общее решение. Обозначим
и найдем его общее решение. Обозначим 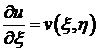 , тогда уравнение примет вид
, тогда уравнение примет вид  . Полагая
. Полагая  фиксированным, проинтегрируем уравнение
фиксированным, проинтегрируем уравнение
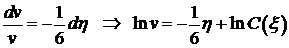

 .
.
Осталось при фиксированном  проинтегрировать уравнение
проинтегрировать уравнение
 .
.
Значит, общее решение можно записать в виде
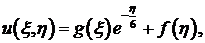
где  произвольные функции.
произвольные функции.
Возвращаясь к переменным 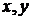 , запишем общее решение уравнения в виде:
, запишем общее решение уравнения в виде:
 (*)
(*)
Найдем
 (**)
(**)
Полагая 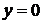 в выражениях (*) и (**) и используя начальные условия, получаем систему для определения вида функций
в выражениях (*) и (**) и используя начальные условия, получаем систему для определения вида функций 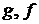 :
:
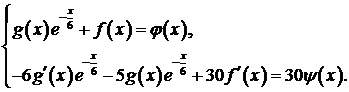
Дифференцируем первое уравнение: 
и прибавляем к нему второе, записанное в виде

Получим 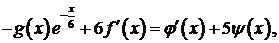 что позволяет во втором уравнении системы два слагаемых в левой части заменить известными функциями:
что позволяет во втором уравнении системы два слагаемых в левой части заменить известными функциями:
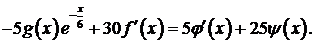
В результате второе уравнение системы принимает вид
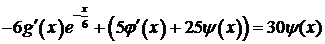 ,
,
откуда определяем  . Интегрируя, находим
. Интегрируя, находим 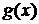 :
:

Из первого уравнения системы определяем функцию  :
:

Остается подставить функции 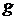 и
и 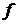 с аргументами соответственно
с аргументами соответственно 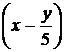 и
и 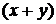 в (*) и записать решение задачи Коши:
в (*) и записать решение задачи Коши:
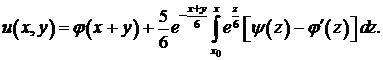
В частном случае при 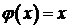 ,
,  решение принимает вид
решение принимает вид  .
.
Непосредственной проверкой убеждаемся, что эта функция удовлетворяет и уравнению, и начальным условиям.●
Задача 4. Найти решение уравнения
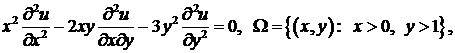
удовлетворяющее начальным условиям 
Решение. Здесь  в
в 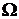 (гиперболический тип в
(гиперболический тип в 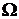 ). Составляем уравнение характеристик
). Составляем уравнение характеристик


Оно распадается на два: 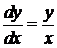 и
и 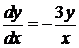 . Находим общие интегралы:
. Находим общие интегралы:
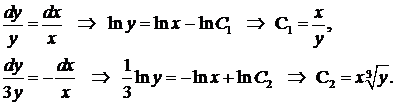
После введения новых переменных 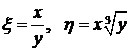 и пересчета производных уравнение принимает вид
и пересчета производных уравнение принимает вид 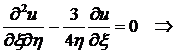

Найдем общее решение этого уравнения. Если введем обозначение 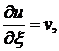 то
то  Уравнение
Уравнение  интегрируем по
интегрируем по  при фиксированном
при фиксированном  .
.
 ,
, 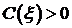

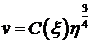
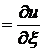 .
.
Затем фиксируем  и интегрируем по
и интегрируем по  :
:

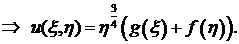
Осталось вернуться к старым переменным и записать общее решение в виде:
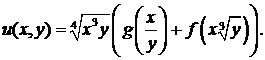
Здесь 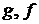 – произвольные функции, определяемые из начальных условий.
– произвольные функции, определяемые из начальных условий.
Найдем 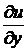 :
: 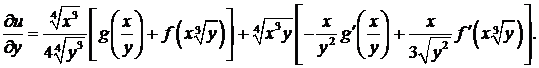
Воспользуемся начальными условиями:
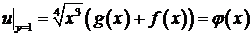
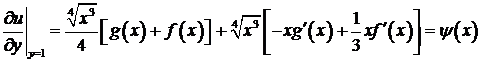
Для определения вида функций  получили систему
получили систему
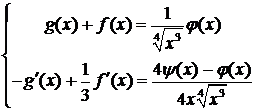
из которой находим
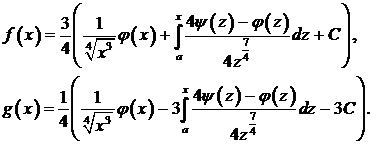
Теперь решение задачи Коши запишется (следим за аргументами!) в виде:


После несложных преобразований получаем ответ:
 ●
●
Физическая интерпретация
А). Распространение волны отклонения
При нулевой начальной скорости 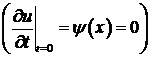 из формулы Даламбера получаем
из формулы Даламбера получаем
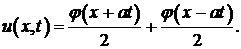
В этом случае колебания представляют собой процесс распространения начального отклонения 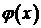 .
.
Функция вида 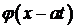 в физике называется распространяющейся волной – неизменный профиль
в физике называется распространяющейся волной – неизменный профиль 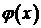 перемещается вправо со скоростью
перемещается вправо со скоростью  . Аналогично функция
. Аналогично функция 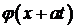 представляет неизменный профиль
представляет неизменный профиль 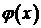 , перемещающийся влево со скоростью
, перемещающийся влево со скоростью  .
.
Значит, решение 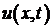 представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью
представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью  , и обратной, бегущей влево с той же скоростью. При этом начальная форма обеих волн определяется функцией
, и обратной, бегущей влево с той же скоростью. При этом начальная форма обеих волн определяется функцией 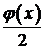 – половиной начального отклонения
– половиной начального отклонения 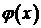 .
.
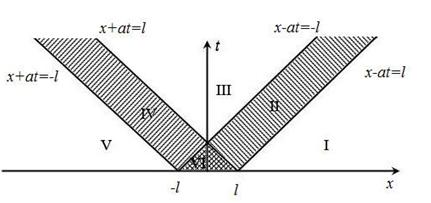 Рассмотрим фазовую плоскость
Рассмотрим фазовую плоскость  .
.
Линии  суть характеристики. Функция
суть характеристики. Функция 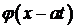 сохраняет постоянное значение на характеристиках
сохраняет постоянное значение на характеристиках 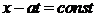 , а функция
, а функция 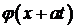 – на характеристиках
– на характеристиках 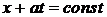 .
.
Предположим, что начальное отклонение отлично от нуля только в промежутке 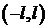 , а вне этого промежутка равно нулю.
, а вне этого промежутка равно нулю.
Характеристики 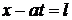 и
и 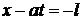 представляют собой передний и задний фронты прямой волны, а характеристики
представляют собой передний и задний фронты прямой волны, а характеристики 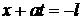 и
и 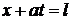 – соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область
– соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область 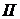
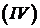 проходит прямая (обратная) волна, а в области
проходит прямая (обратная) волна, а в области 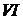 взаимодействуют обе волны. В область
взаимодействуют обе волны. В область 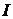 (и
(и 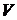 ) до некоторого момента времени
) до некоторого момента времени 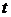 еще не дошла прямая (обратная) волна; через область
еще не дошла прямая (обратная) волна; через область 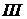 с некоторого момента
с некоторого момента 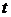 волны уже прошли и наступил покой.
волны уже прошли и наступил покой.
Б). Распространение волны импульса
При нулевом начальном отклонении 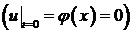 колебания вызываются начальной скоростью (или импульсом)
колебания вызываются начальной скоростью (или импульсом) 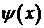 и решение задачи Коши можно представить в виде разности обратной и прямой волны:
и решение задачи Коши можно представить в виде разности обратной и прямой волны:
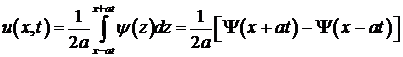
Здесь 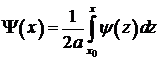 – первообразная функции
– первообразная функции 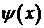 .
.
Например, пусть 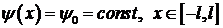 и
и 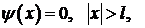 тогда
тогда
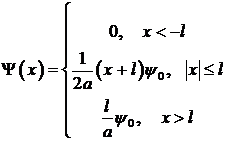
Графики функций 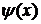 и
и 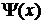 приведены на рисунке.
приведены на рисунке.
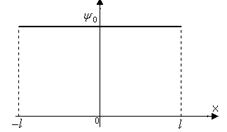
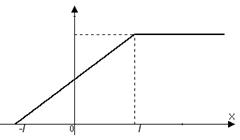
Начальный импульс 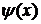 Функция
Функция 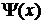 – профиль волны
– профиль волны





 (1)
(1)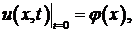

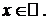 (2)
(2)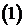 к каноническому виду. Уравнение характеристик
к каноническому виду. Уравнение характеристик  распадается на два уравнения:
распадается на два уравнения:  и
и 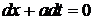 . Общие интегралы этих уравнений суть семейства прямых
. Общие интегралы этих уравнений суть семейства прямых 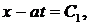
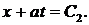 Вводим новые переменные
Вводим новые переменные 
 и пересчитываем производные:
и пересчитываем производные: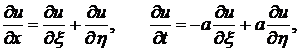

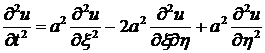
 Интегрирование уравнение
Интегрирование уравнение  по
по  при фиксированном
при фиксированном  даёт общий интеграл в виде
даёт общий интеграл в виде  . Здесь
. Здесь  произвольная функция. Повторно интегрируем по
произвольная функция. Повторно интегрируем по  .
. и
и  произвольные функции. Возвращаясь к старым переменным, получаем, что общим решением уравнения
произвольные функции. Возвращаясь к старым переменным, получаем, что общим решением уравнения  (3)
(3) определяется из начальных условий
определяется из начальных условий 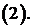
 . В силу первого начального условия
. В силу первого начального условия 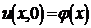 получаем
получаем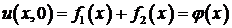 .
. по переменной
по переменной 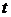 :
:
 получаем
получаем .
. 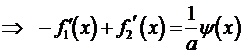 .
.
 фиксированное значение независимой переменной
фиксированное значение независимой переменной 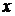 ,
, 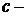 произвольная постоянная.
произвольная постоянная.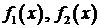 определяется из системы уравнений
определяется из системы уравнений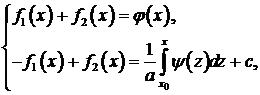



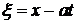 , а функция
, а функция  , и подставить найденные функции в представление
, и подставить найденные функции в представление 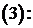
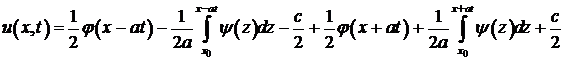
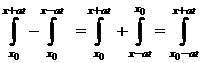 , получим окончательно
, получим окончательно (4)
(4) носит название формулы Даламбера.
носит название формулы Даламбера.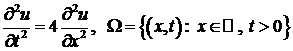 ,
,
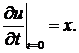
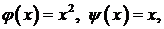
 , тогда
, тогда 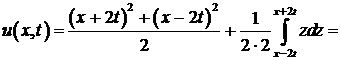
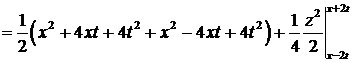 .
.
 действительно есть решение задачи Коши, т.е. удовлетворяет и уравнению, и начальным условиям. ●
действительно есть решение задачи Коши, т.е. удовлетворяет и уравнению, и начальным условиям. ● (5)
(5) (6)
(6)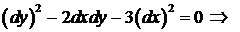
 .
. и
и 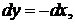 общие интегралы которых удобно записать в виде:
общие интегралы которых удобно записать в виде:  . Вводим новые переменные
. Вводим новые переменные 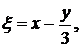
 и пересчитываем производные функции
и пересчитываем производные функции  :
: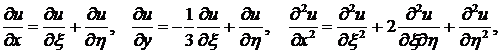
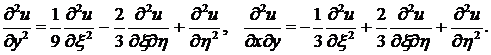
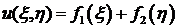 , где
, где  – произвольные функции. Значит, для исходного уравнения
– произвольные функции. Значит, для исходного уравнения (7)
(7)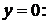
 .
.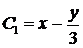 , т.е.
, т.е.  – при
– при 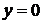 получаем
получаем  . Если бы
. Если бы  , то
, то 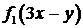 и при
и при  .
. по
по 
 .
.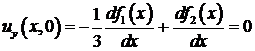
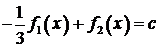 .
.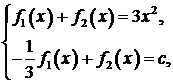 находим вид функций
находим вид функций 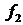 :
: ,
, 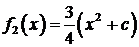 .
.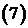 . При этом следует помнить, что у функция
. При этом следует помнить, что у функция 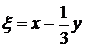 , а у функции
, а у функции  . Получаем:
. Получаем: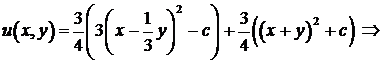
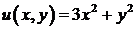 .
.
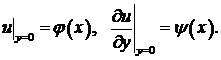
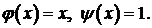
 распадается на два уравнения:
распадается на два уравнения: 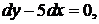 и
и  . Общие интегралы удобнее записать в виде:
. Общие интегралы удобнее записать в виде: 
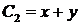 . Новые переменные
. Новые переменные  . Дифференцируем сложную функцию
. Дифференцируем сложную функцию 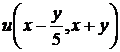 :
:

 и найдем его общее решение. Обозначим
и найдем его общее решение. Обозначим 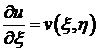 , тогда уравнение примет вид
, тогда уравнение примет вид  . Полагая
. Полагая 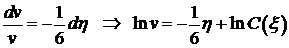
 .
. .
.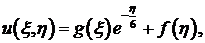
 произвольные функции.
произвольные функции.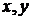 , запишем общее решение уравнения в виде:
, запишем общее решение уравнения в виде: (*)
(*) (**)
(**)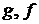 :
: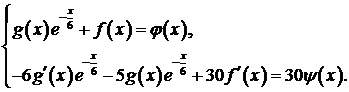


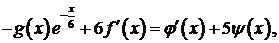 что позволяет во втором уравнении системы два слагаемых в левой части заменить известными функциями:
что позволяет во втором уравнении системы два слагаемых в левой части заменить известными функциями: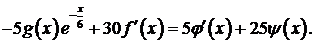
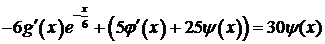 ,
, . Интегрируя, находим
. Интегрируя, находим 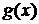 :
:
 :
:
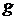 и
и 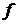 с аргументами соответственно
с аргументами соответственно 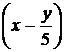 и
и 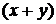 в (*) и записать решение задачи Коши:
в (*) и записать решение задачи Коши: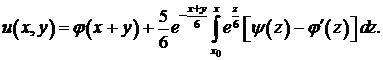
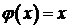 ,
,  решение принимает вид
решение принимает вид  .
.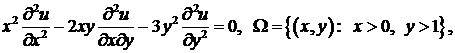

 в
в 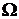 (гиперболический тип в
(гиперболический тип в 

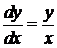 и
и 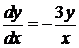 . Находим общие интегралы:
. Находим общие интегралы: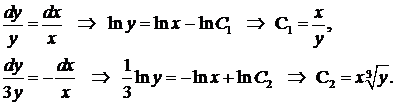
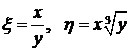 и пересчета производных уравнение принимает вид
и пересчета производных уравнение принимает вид 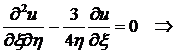

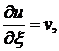 то
то  Уравнение
Уравнение  интегрируем по
интегрируем по  ,
, 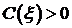
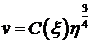
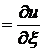 .
.
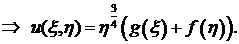
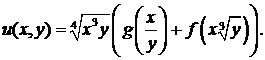
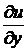 :
: 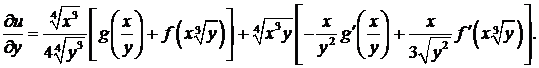
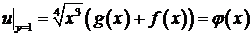
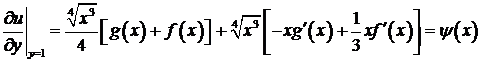
 получили систему
получили систему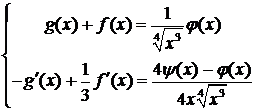
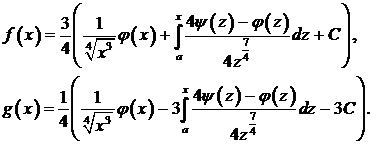


 ●
● из формулы Даламбера получаем
из формулы Даламбера получаем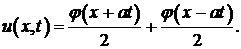
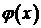 .
.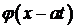 в физике называется распространяющейся волной – неизменный профиль
в физике называется распространяющейся волной – неизменный профиль  . Аналогично функция
. Аналогично функция 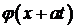 представляет неизменный профиль
представляет неизменный профиль 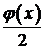 – половиной начального отклонения
– половиной начального отклонения  Рассмотрим фазовую плоскость
Рассмотрим фазовую плоскость  .
.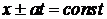 суть характеристики. Функция
суть характеристики. Функция 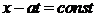 , а функция
, а функция 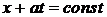 .
.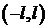 , а вне этого промежутка равно нулю.
, а вне этого промежутка равно нулю.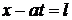 и
и 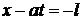 представляют собой передний и задний фронты прямой волны, а характеристики
представляют собой передний и задний фронты прямой волны, а характеристики 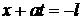 и
и 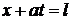 – соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область
– соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область 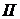
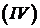 проходит прямая (обратная) волна, а в области
проходит прямая (обратная) волна, а в области 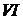 взаимодействуют обе волны. В область
взаимодействуют обе волны. В область 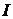 (и
(и 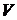 ) до некоторого момента времени
) до некоторого момента времени 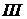 с некоторого момента
с некоторого момента 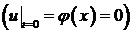 колебания вызываются начальной скоростью (или импульсом)
колебания вызываются начальной скоростью (или импульсом) 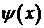 и решение задачи Коши можно представить в виде разности обратной и прямой волны:
и решение задачи Коши можно представить в виде разности обратной и прямой волны: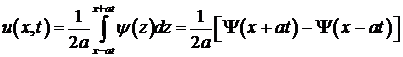
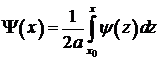 – первообразная функции
– первообразная функции 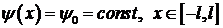 и
и 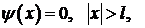 тогда
тогда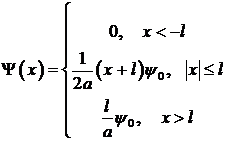
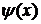 и
и 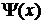 приведены на рисунке.
приведены на рисунке.




