Сходимость приближенного решения к точному означает, что
(1)  ,
,
однако более информативным является оценка вида:
(2)  .
.
Предполагаем, что сетка 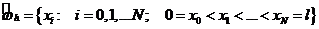 уже построена и
уже построена и 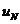 определена в
определена в  и поставлена задача (3).
и поставлена задача (3).
(3)  ,
,  .
.
Тогда имеет место следующая теорема.
Теорема 1
Пусть  и
и 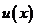 точное решение задачи:
точное решение задачи:
В классической постановке:
(4) 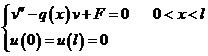
В обобщенной постановке:
(5) 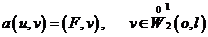 ,
,
(6)  ,
,

Тогда, если 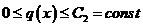 , то выполняется неравенство:
, то выполняется неравенство:
(7) 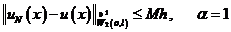 ,
,  и не зависит от шага сетки.
и не зависит от шага сетки.
Доказательство:
(8) 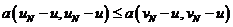 .
.
Идея доказательства эксплуатирует в первую очередь неравенство (8), где вместо  выбирается функция
выбирается функция 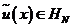 , являющаяся кусочно-линейным восполнением точного решения
, являющаяся кусочно-линейным восполнением точного решения 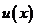 , т.е.
, т.е.  , где
, где 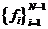 - базис. Также используются неравенства (10), (11) и (12).
- базис. Также используются неравенства (10), (11) и (12).
Согласно леммам 1 и 2 §1 “Кусочно-линейные восполнения сеточных функций”, имеем:
(9)  .
.
(10)  .
.
Справедливо:


учитывая (9) и (10) получаем:
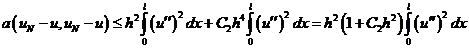
(11)  .
.
Напомним, неравенство (11) предыдущего параграфа:
(12) 
Преобразуем левую часть полученного неравенства с учетом неравенства (12).
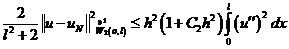 .
.
Имеем:
(13)  .
.
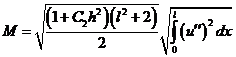 , требуемая оценка (7) получена.
, требуемая оценка (7) получена.
Оценка (13) которая была компактно записана как (7) означает сходимость построенной схемы в среднем. Опираясь на нее, а также на неравенство (9), (10) предыдущего параграфа можно получить оценку для равномерной сходимости последовательности 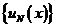 к
к 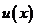 . Справедливо следствие.
. Справедливо следствие.
Следствие
Последовательность 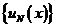 приближенных решений сходится равномерно на отрезке
приближенных решений сходится равномерно на отрезке  при
при 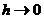 ,
, 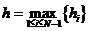 к точному решению с первым порядком, т.е. справедлива оценка:
к точному решению с первым порядком, т.е. справедлива оценка:
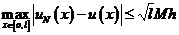
Заключение по модулю
Первый модуль учебника является основным для дальнейшего понимания курса. Показаны и исследованы методы аппроксимации непрерывных физических моделей конечно-разностными и конечно-элементными аналогами. Исследуется корректность операторных уравнений. Приводятся основные определения и теоремы.
При изложении материала данного модуля использовались разделы линейной алгебры, функционального анализа и математической физики.
Вопросы для самоконтроля
1) Понятие консервативной разностной схемы.
2) Понятие погрешности аппроксимации, устойчивости и сходимости разностной схемы. Теорема Лакса- Филиппова.
3) Основные разностные тождества. Формулы разностного дифференцирования произведения. Разностные формулы Грина.
4) Свойства собственных чисел оператора разностной производной второго порядка.
5) Разностные схемы для уравнения теплопроводности. Исследование устойчивости. Условие FCL для явных разностных схем.
6) Принцип максимума сеточных функций. Следствия.
7) Теорема сравнения. Мажоранта.
8) Определение корректно поставленной разностной модели.
9) Теорема о равномерной устойчивости двухслойных разностных схем. Основное энергетическое тождество.
10) Экономичные разностные схемы для нестационарных задач.
11) Понятие о методе конечных элементов.
1.10. Проектное задание
Упражнение 1. Найдите решение краевой задачи:
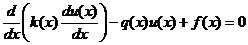 , с переменными коэффициентами
, с переменными коэффициентами
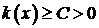 ,
, 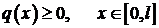 и граничными условиями
и граничными условиями


на основе решения задач Коши.
Упражнение 2. Постройте схему четвертого порядка аппроксимации
для уравнения
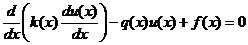 , k(x)=1 на равномерной сетке
, k(x)=1 на равномерной сетке
при использовании трехточечного шаблона.
Упражнение 3. Сформулируйте условие устойчивости явной трехслойной
схемы второго порядка аппроксимации по времени и пространству для задачи
u(x,t) = v0 (x), 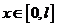
 ,
, 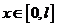 .
.
Контрольная работа №1.
Вариант №1.
1. Интегро-интерполяционным методом построить консервативную разностную схему для краевой задачи
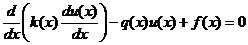 ,
, 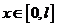
г.у. 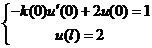
 ,
,  ,
, 
на равномерной сетке 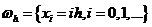 , где
, где  ,
,  .
.
2. Методом гармоник исследовать устойчивость разностной схемы
 ,
,
на равномерной сетке  , при 1)
, при 1)  2)
2) 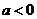 .
.
3*. Построить непрерывный аналог схемы
 ,
,
имеющей следующий порядок аппроксимации  .
.
Вариант №2.
1. Интегро-интерполяционным методом построить консервативную разностную схему для краевой задачи
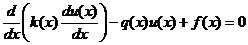 ,
, 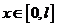
г.у. 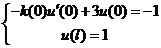
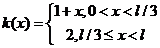 ,
,  ,
, 
на равномерной сетке 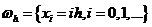 , где
, где 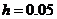 ,
, 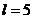 .
.
2. Методом гармоник исследовать устойчивость разностной схемы
 ,
,
на равномерной сетке  , при 1)
, при 1)  2)
2) 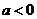 .
.
3*. Найти условие применимости прогонки для решения разностной задачи
 ,
, 
на равномерной сетке 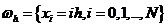 , где
, где  .
.
Вариант №3.
1. Интегро-интерполяционным методом построить консервативную разностную схему для краевой задачи
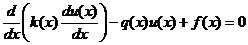 ,
, 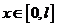
г.у. 
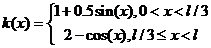 ,
,  ,
, 
на равномерной сетке 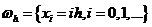 , где
, где 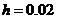 ,
,  .
.
2. Методом гармоник исследовать устойчивость разностной схемы
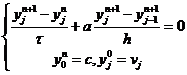 ,
,
на равномерной сетке  , при 1)
, при 1)  2)
2) 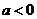 .
.
3*. Найти условие применимости прогонки для решения разностной задачи
 ,
, 
на равномерной сетке 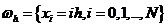 , где
, где  .
.
Вариант №4.
1. Интегро-интерполяционным методом построить консервативную разностную схему для краевой задачи
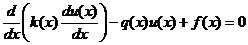 ,
, 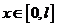
г.у. 
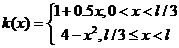 ,
, 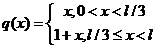 ,
, 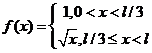
на равномерной сетке 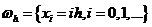 , где
, где 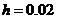 ,.
,. 
2. Методом гармоник исследовать устойчивость разностной схемы
 ,
,
на равномерной сетке  , при 1)
, при 1)  2)
2) 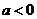 .
.
3*. Найти условие применимости прогонки для решения разностной задачи
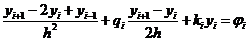 ,
, 
на равномерной сетке 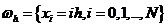 , где
, где  .
.
Вариант №5.
1. Интегро-интерполяционным методом построить консервативную разностную схему для краевой задачи
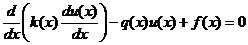 ,
, 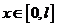
г.у. 
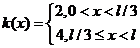 ,
,  ,
, 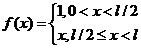
на равномерной сетке 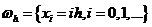 , где
, где 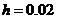 ,
,  .
.
2. Методом гармоник исследовать устойчивость разностной схемы
 ,
,
на равномерной сетке  , при 1)
, при 1)  2)
2) 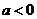 .
.
3*. Построить непрерывный аналог схемы
 ,
,  ,
,
имеющей следующий порядок аппроксимации  .
.
Контрольная работа №2.
Вариант №1.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.
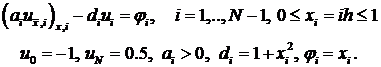
2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным.
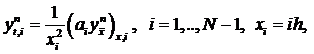
где  , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые
3. Используя шаблон 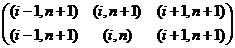 построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения 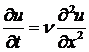 , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Вариант №2.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.

2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным

где  ,
,  , н.у. заданы, г.у. нулевые.
, н.у. заданы, г.у. нулевые.
3. На шаблоне  построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Вариант №3.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.
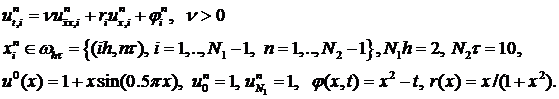
2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным.

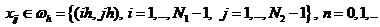 , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые
3. Используя шаблон  построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Вариант №4.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.
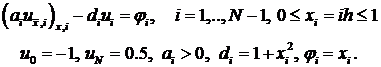
2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным

где  ,
,  , н.у. заданы, г.у. нулевые.
, н.у. заданы, г.у. нулевые.
3. Используя шаблон  построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Вариант №5.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.
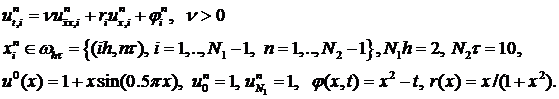
2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным.
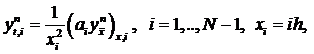
где  , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые
3. На шаблоне  построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Вариант №6.
1. Оценить решение и найти условие устойчивости разностной схемы, используя принцип максимума и следствия из него.

2. Привести разностную схему к каноническому виду и исследовать устойчивость по начальным данным.

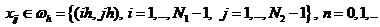 , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые
2. Используя шаблон 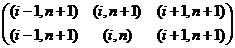 построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения 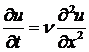 , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.
Тест рубежного контроля
1) Вопрос: Какое из приведенных выражений является скалярным произведением сеточных функций:
1.  2.
2.  3.
3. 
2) Вопрос: Какая из приведенных ниже разностных схем для уравнения теплопроводности является неявной:
1. 
2. 
3. 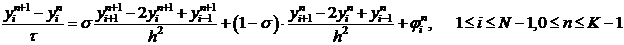
3) Вопрос: Что означает принцип максимума для  :
:
1. Сеточная функция y (P) не может достигать наименьшего отрицательного значения во внутренних узлах сетки.
2. Сеточная функция y (P) не может достигать наибольшего положительного значения во внутренних узлах сетки.
3. Сеточная функция y (P) постоянная.
4) Вопрос: Оператор A называется кососимметричным, если:
1. 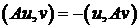 2.
2. 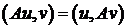 3.
3. 
5) Вопрос: Для равномерной устойчивости схемы вида:
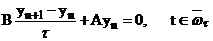 ,
, 

Необходимо и достаточно выполнение следующего операторного неравенства:
1.  2.
2. 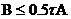 3.
3. 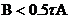
6) Вопрос: оператор А называется строго положительно определенным, если:
1.  2.
2.  3.
3. 
7) Вопрос: операторное уравнение называется корректным, если:
1. Решение существует, единственно и непрерывно зависит от начальных данных.
2. Уравнение имеет повышенный порядок аппроксимации.
3. Решение операторного уравнения сходится к решению дифференциальной задачи.
8) Вопрос: для линейных разностных задач из аппроксимации и устойчивости следует:
1. Консервативность разностной схемы.
2. Сходимость разностной схемы.
3. Монотонность разностной схемы.
9) Вопрос: из принципа максимума следует, что сеточное уравнение
 с граничными условиями
с граничными условиями 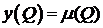 имеет:
имеет:
1. Единственное решение.
2. Тривиальное решение.
3. Положительное решение.
10) Вопрос: достаточным условием ρ – сходимости схемы является:
1. Корректность поставленной задачи.
2. Обычная устойчивость задачи.
3. Ограниченность оператора перехода.
Бланк правильных ответов
| № вопрс. / № отв.
| 1
| 2
| 3
|
| 1
|
| *
|
|
| 2
|
| *
|
|
| 3
|
| *
|
|
| 4
| *
|
|
|
| 5
| *
|
|
|
| 6
|
|
| *
|
| 7
| *
|
|
|
| 8
|
| *
|
|
| 9
| *
|
|
|
| 10
|
|
| *
|
Оценка: за девять или десять правильных ответов – отлично.
За семь правильных ответов - хорошо.
За шесть правильных ответов – удовлетворительно.
Остальное число ответов оценивается неудовлетворительно.



 ,
, .
.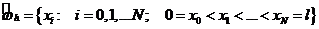 уже построена и
уже построена и 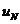 определена в
определена в  и поставлена задача (3).
и поставлена задача (3). ,
,  .
. и
и 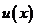 точное решение задачи:
точное решение задачи: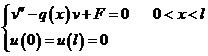
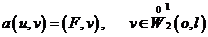 ,
, ,
,
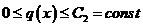 , то выполняется неравенство:
, то выполняется неравенство: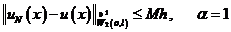 ,
,  и не зависит от шага сетки.
и не зависит от шага сетки.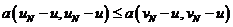 .
. выбирается функция
выбирается функция 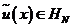 , являющаяся кусочно-линейным восполнением точного решения
, являющаяся кусочно-линейным восполнением точного решения  , где
, где 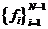 - базис. Также используются неравенства (10), (11) и (12).
- базис. Также используются неравенства (10), (11) и (12). .
. .
.

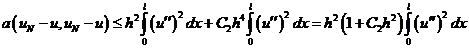
 .
.
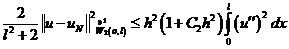 .
. .
.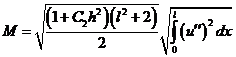 , требуемая оценка (7) получена.
, требуемая оценка (7) получена.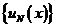 к
к  при
при 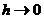 ,
, 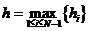 к точному решению с первым порядком, т.е. справедлива оценка:
к точному решению с первым порядком, т.е. справедлива оценка: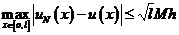
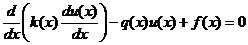 , с переменными коэффициентами
, с переменными коэффициентами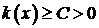 ,
, 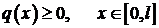 и граничными условиями
и граничными условиями

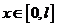
 ,
, 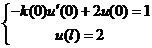
 ,
,  ,
, 
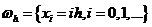 , где
, где  ,
,  .
. ,
,  , при 1)
, при 1)  2)
2) 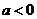 .
. ,
, .
.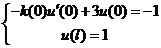
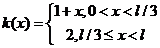 ,
,  ,
, 
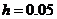 ,
, 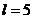 .
. ,
,  ,
, 
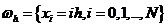 , где
, где  .
.
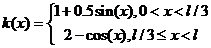 ,
,  ,
, 
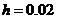 ,
,  .
.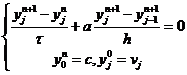 ,
,  ,
, 
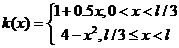 ,
, 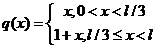 ,
, 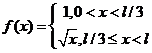

 ,
, 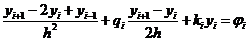 ,
, 
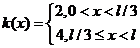 ,
,  ,
, 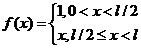
 ,
,  ,
,  ,
, .
.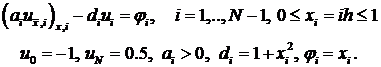
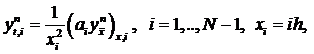
 , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые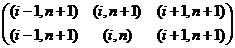 построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения 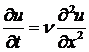 , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.

 ,
,  , н.у. заданы, г.у. нулевые.
, н.у. заданы, г.у. нулевые. построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
.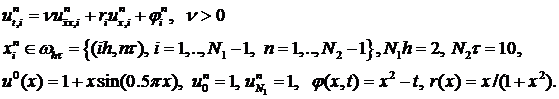

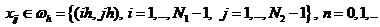 , н.у. заданы, г.у. нулевые
, н.у. заданы, г.у. нулевые построить компактную разностную схему для уравнения
построить компактную разностную схему для уравнения  , имеющую погрешность аппроксимации
, имеющую погрешность аппроксимации  .
. 2.
2.  3.
3. 


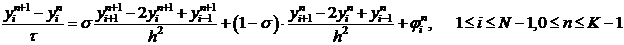
 :
: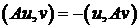 2.
2. 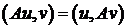 3.
3. 
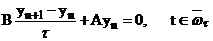 ,
, 

 2.
2. 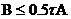 3.
3. 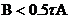
 2.
2.  3.
3. 
 с граничными условиями
с граничными условиями 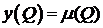 имеет:
имеет:


