

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Как правило, дискретизация пространственных производных первого и второго порядка приводит к несамосопряженным операторам. Например, в задачах диффузии – конвекции, конвективная часть задачи порождает несамосопряженный оператор.
Рассмотрим частный случай схемы с весами с несамосопряженным оператором.
(1) 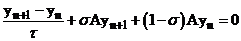
(2)  ,
, 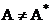 .
.
 - весовой параметр.
- весовой параметр.
Достаточное условие устойчивости по начальным данным с  .
.
Теорема 1
Схема (1), (2) 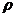 - устойчива с
- устойчива с  , если
, если
1. оператор 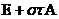 имеет обратный, т.е. существует оператор
имеет обратный, т.е. существует оператор
(3) 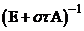 . Достаточным условием является
. Достаточным условием является 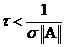 .
.
2. 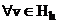 выполняется неравенство
выполняется неравенство
(4) 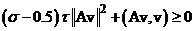 .
.
Для начала докажем вспомогательное утверждение.
Пусть заданы два перестановочных оператора 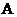 и
и 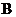 , такие, что
, такие, что 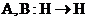 и существует обратный оператор
и существует обратный оператор 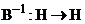 . Тогда операторы
. Тогда операторы 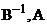 также являются перестоновочными, т.е.
также являются перестоновочными, т.е.
(5) 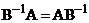
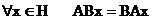 умножим слева на
умножим слева на 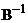 , тогда
, тогда 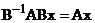 , обозначим
, обозначим 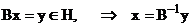 , тогда
, тогда 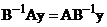 . Элемент
. Элемент 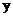 произвольный за счет выбора
произвольный за счет выбора 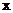 .
.
Доказательство:
Для задачи (1) требуется доказать оценку 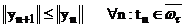 .
.
Надо получить: 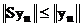 , а, следовательно, и
, а, следовательно, и 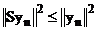 . Т.е. надо доказать
. Т.е. надо доказать
(6)  при выполнении (3), (4).
при выполнении (3), (4).
 - оператор перехода от
- оператор перехода от 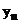 к
к  , т.е.
, т.е. 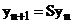 .
.
Далее задача (1), (2) будет записана в канонической форме двухслойных схем, а именно:
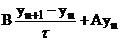
 ;
;
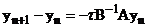 ;
;
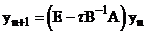 .
.
Итак, оператор 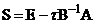 .
.
С учетом (6) мы хотим доказать (4).
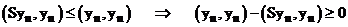 .
.
Вычислим
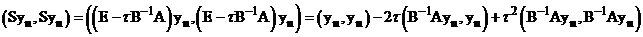 .
.
Очевидно, соотношение (7), с учетом (6) приводит к неравенству:
 .
.
(8) 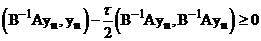 .
.
Так как 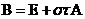 , то операторы
, то операторы  перестановочные
перестановочные 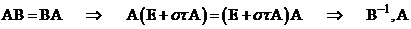 - перестоновочные.
- перестоновочные.
Неравенство (8) запишется
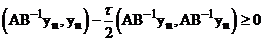 .
.
Введем вектор 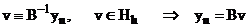 , тогда
, тогда
 ,
,
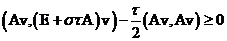
 ,
,
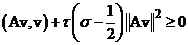 что и требовалось доказать.
что и требовалось доказать.
Получим, что если 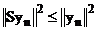 , то выполняется (4) с
, то выполняется (4) с  .
.
Замечание.
1. Заметим, что неравенство (4) выполняется, если 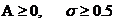 . В частности, если оператор
. В частности, если оператор 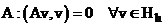 , т.е. кососимметрический, то (4) выполняется для любого параметра
, т.е. кососимметрический, то (4) выполняется для любого параметра 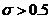 .
.
|
|
2. Условие обратимости оператора 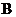 может оказаться достаточно жестким в случае произвольного оператора
может оказаться достаточно жестким в случае произвольного оператора 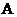 . В случае
. В случае 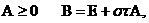
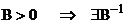 . Если оператор
. Если оператор 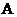 незнакоопределен, тогда вопрос обратимости оператора
незнакоопределен, тогда вопрос обратимости оператора 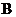 решается на основе известной теоремы функционального анализа:
решается на основе известной теоремы функционального анализа:
Теорема.
С – оператор из банахова пространства в банахово. Е и С – линейные операторы. Оператор  имеет обратный оператор
имеет обратный оператор 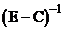 , если
, если 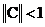 . При этом выполняется оценка:
. При этом выполняется оценка: 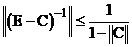 .
.
В нашем случае 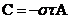 .
.
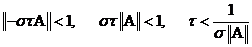 , что является жестким ограничением на шаг по времени.
, что является жестким ограничением на шаг по времени.
И в случае явной схемы для уравнения теплопроводности 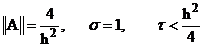 .
.
Если использовать неравенство  , то
, то 
Иногда обратимость оператора В является более жестким ограничением на шаг по времени, чем условие (4).
Пример 1.
Рассмотрим уравнение теплопроводности.
(*) 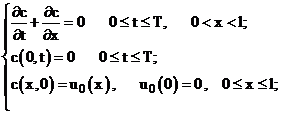
поставим в соответствие непрерывной задаче дискретную задачу:
(**) 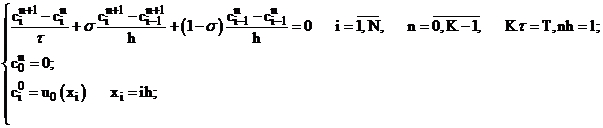
Дискретную задачу можно записать в операторной форме для уравнения с весами с несамосопряженным оператором.
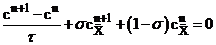 .
.
Оператор 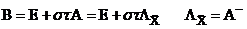 .
.
Заметим, что
1. 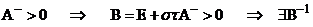 ;
;
2. было вычислено соотношение
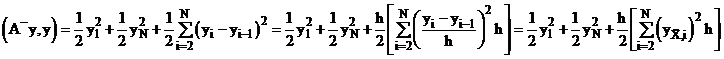 (9)
(9) 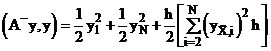 .
.
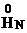 -гильбертово пространство сеточных функций, определенных на сетке
-гильбертово пространство сеточных функций, определенных на сетке 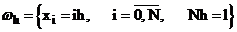 , таких, что обращаются в ноль при i=0.
, таких, что обращаются в ноль при i=0.
Формула (9) может быть преобразована, если учесть что  .
.
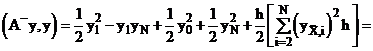
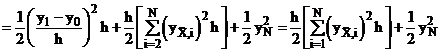 .
.
Получили
(10) 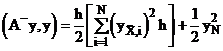 ,
,  .
.
Можно воспользоваться неравенством (4).
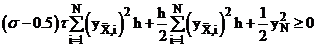 ,
,
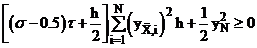 неравенство выполняется для любых
неравенство выполняется для любых 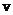 тогда и только тогда, когда
тогда и только тогда, когда 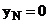 , получим,
, получим,
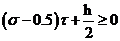 , из этого неравенства получаем допустимые
, из этого неравенства получаем допустимые 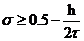 .
.
__________________________________________________________
‼ Доказать самостоятельно что схема при 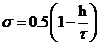 имеет порядок аппроксимации
имеет порядок аппроксимации 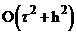 .
.
__________________________________________________________
На практике очень часто встречаются схемы вида:
(11) 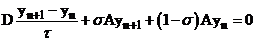
(12)  .
.
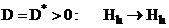 .
.
Если 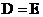 то мы получаем схему с весами (1), (2) из теоремы 1.
то мы получаем схему с весами (1), (2) из теоремы 1.
Введем пространство 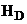 в котором норма унифицирована оператором
в котором норма унифицирована оператором 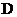 .
.
(13) 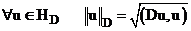 .
.
Сформулируем теорему о равномерной устойчивости с 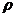 - устойчивостью для схемы (11), (12) с
- устойчивостью для схемы (11), (12) с  .
.
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!