Эти схемы сочетают достоинства явных и неявных схем:
ü Абсолютно устойчивы, т.е. устойчивы при любых значениях шага по времени;
ü Являются экономичными схемами. Это означает, что затраты арифметических операций на получение значения функции  , если все значения
, если все значения  известны, есть величина
известны, есть величина  арифметических операций.
арифметических операций.
Рассмотрим смешанную задачу Коши для уравнения теплопроводности в прямоугольнике.
В области 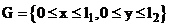 требуется найти решение уравнения:
требуется найти решение уравнения:
(1) 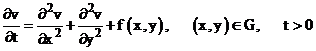 ,
,
если заданы граничные условия:
(2) 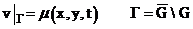
(3) 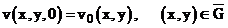 .
.
Рассматриваем случай, когда  .
.
Для аппроксимации задачи (1), (2), область  покроем равномерной сеткой с шагами
покроем равномерной сеткой с шагами  по оси Ох и
по оси Ох и  по оси Оу.
по оси Оу.
 ,
,
 ,
,
 .
.
Так как уравнение с постоянными коэффициентами, то будем использовать непосредственную аппроксимацию специального вида.
Введем вспомогательную сетку
 .
.
Будем использовать так называемую схему Писмена – Рекфорда.
Схема Писмена – Рекфорда.
(4)  ,
,
(5) 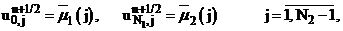
(6)  ,
,
(7)  ,
,
(8)  .
.
Задача (4) представляет собой систему трех точечных уравнений относительно функции  . Если все
. Если все  известны, то система (4) может быть решена методом прогонки. Данный метод является экономичным
известны, то система (4) может быть решена методом прогонки. Данный метод является экономичным  операций. Прогонки выполняются вдоль строк. Если все
операций. Прогонки выполняются вдоль строк. Если все  найдены, то решая задачу (8) относительно функции
найдены, то решая задачу (8) относительно функции  , задача которая также представляет собой систему трех точечных уравнений, заканчивая цикл вычислений к переходу на
, задача которая также представляет собой систему трех точечных уравнений, заканчивая цикл вычислений к переходу на  временной слой. Затраты на арифметические операции составят
временной слой. Затраты на арифметические операции составят  , прогонки выполняются вдоль столбцов. Тогда общее число операций составит порядка
, прогонки выполняются вдоль столбцов. Тогда общее число операций составит порядка 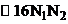 операций.
операций.
Исследуем устойчивость схемы (6), (7) энергетическим методом. Попутно установим вид функций  .
.
Запишем уравнения (4), (6) в операторном виде относительно пространственных переменных.
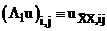 ,
,
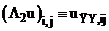 .
.
(4′) 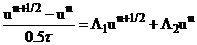 ,
,
(6′) 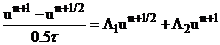 .
.
Операторы 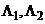 в гильбертовом пространстве сеточных функций определенных на сетке
в гильбертовом пространстве сеточных функций определенных на сетке 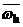 и обращающихся в ноль в узлах
и обращающихся в ноль в узлах 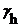 являются самосопряженными, и отрицательно определенными, т.е.
являются самосопряженными, и отрицательно определенными, т.е.  .
.
Кроме того, не трудно показать, что эти операторы коммутативны, т.е.  .
.
Свойство коммутативности выполняется только для специальной геометрии области. Область  должна быть односвязной областью ступенчатой формы, границы которой являются отрезками прямых параллельных координатным осям. Также накладываются ограничения на тип граничных условий. Для граничных условий 3-го рода коммутативность не выполняется.
должна быть односвязной областью ступенчатой формы, границы которой являются отрезками прямых параллельных координатным осям. Также накладываются ограничения на тип граничных условий. Для граничных условий 3-го рода коммутативность не выполняется.
Вычтем из (4) равенство (6).
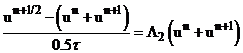 , выразим
, выразим 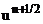
(9) 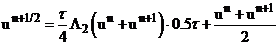 .
.
Последнее равенство позволяет нам определить вид функций  .
.
Положим в (9) 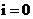 , тогда
, тогда
 .
.
Примем во внимание граничное условие (2) исходной задачи.
(10) 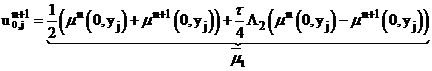
(11)  .
.
Используя соотношения (4), (6) и (9), получим каноническую форму двухслойной схемы.
Сложим (4) и (6).
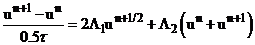 , подставим (9) – выраженное ранее
, подставим (9) – выраженное ранее 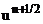 .
.
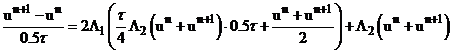 ,
,
 ,
,
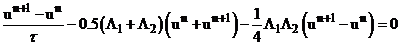 .
.
Общий вид канонической формы:
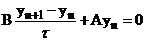 .
.
Выполним очевидные преобразования.
 ,
,
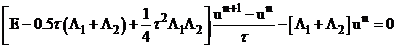 .
.
Введем оператор 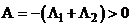 ,
,  ,
, 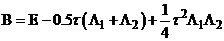 ,
, 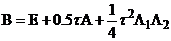 .
.
Проверим операторное неравенство  .
.
 , т.к.
, т.к. 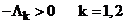 , то
, то  .
.
Поскольку  и
и  , то
, то  неравенство выполняется. Следовательно, схема параллельных направлений устойчива в энергетическом пространстве
неравенство выполняется. Следовательно, схема параллельных направлений устойчива в энергетическом пространстве  , где
, где 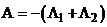 .
.
Замечание.
В явном виде нигде не использовалась коммутативность операторов  , а только положительноопределенность оператора
, а только положительноопределенность оператора 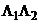 , однако это можно требовать при выполнении коммутативности этих операторов.
, однако это можно требовать при выполнении коммутативности этих операторов.
Лемма.
Пусть  произвольный вектор из
произвольный вектор из 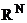 ,
,  - некоторые действительные числа.
- некоторые действительные числа.
Тогда для выполнения неравенства 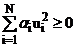 необходимо и достаточно чтобы все
необходимо и достаточно чтобы все 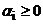 .
.
Факторизованные схемы
Пример 1.
Рассмотренная в предыдущем параграфе схема Писмена – Рекфорда после исключения функции 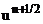 имеет вид:
имеет вид:
(1) 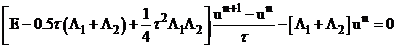 .
.
Выражение  можно представить в виде произведения операторов. Слагаемое
можно представить в виде произведения операторов. Слагаемое  поправляет некорректность задачи.
поправляет некорректность задачи.
(2) 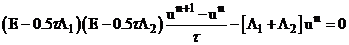
(3)  .
.
Такую запись принято называть факторизованной формой записи схемы.
В некоторых случаях удобно сразу перейти к факторизованной записи двухслойной схемы.
 .
.
Операторы же  должны удовлетворять условиям:
должны удовлетворять условиям: 
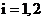 ,
, 
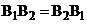 , тогда можно будет применять теорему 1.
, тогда можно будет применять теорему 1.
Имеется еще одно ограничение: операторы  должны быть легко обратимы.
должны быть легко обратимы.
Ограничения на применение факторизованных схем такие же как и для схем переменных направлений.
Замечание.
Формальное обобщение схем переменных направлений на случай трех пространственных координат может приводить, как в схемах Писмена – Рекфорда, к абсолютно неустойчивым схемам.
Стремление уйти от ограничений характерных для схем переменных направлений привело к построению аддитивных схем.
Эти схемы сводят решение многомерных задач к решению цепочки пространственно-одномерных задач.
Рассмотрим задачу Коши для уравнения теплопроводности в  при
при 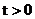 .
.
(1)  ,
,
(2) 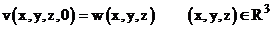 ,
,
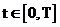 ,рассмотрим вспомогательную сетку
,рассмотрим вспомогательную сетку  наряду с основной.
наряду с основной.
Рассмотрим цепочку одномерных задач вида (3)-(8),  :
:
(3) 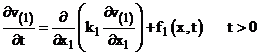 ;
;
(4) 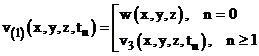
(5) 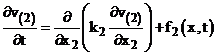 ;
;
(6)  ;
;
(7)  ;
;
(8)  .
.
Аппроксимация данной системы проводится интегро–интерполяционным методом, а сама система экономично решается методом прогонки, в результате получается экономичный метод решения задачи порядка 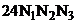 операций.
операций.
К аппроксимации одномерных задач предъявляются следующие требования:
1). 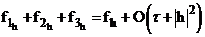 ,
,
2). При этом каждая из правых частей должна быть равномерно ограничена, т.е.  .
.
3). Сумма трех дискретных операторов, являющихся разностными (дискретными) аналогами дифференциальных операторов в (3), (5), (7), должна давать с погрешностью  дискретный аналог задачи (1).
дискретный аналог задачи (1).
Важно отметить, что в отличии от схем переменных направлений, каждая из элементарных задач не приближает исходную задачу (1). Кроме того не требуется перестановочности операторов 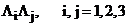 .
.
Замечание.
В общем случае решение задачи (1), (2) и функция 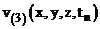 отличается в некоторой норме для
отличается в некоторой норме для  на величину
на величину  .
.
Эти схемы называются аддитивными потому, что свойства выполняются в суммарном смысле.
Схемы применимы для достаточно произвольных областей с кусочно-гладкими границами и переменными коэффициентами.
Рассмотренные выше схемы: переменных направлений, эквивалентные им факторизованные схемы и, наконец, аддитивные схемы, являются представителями схем расщепления по направлению. Наряду с этим активно используются схемы расщепления по физическим процессам.
Рассмотрим для примера нестационарную одномерную задачу диффузии-конвекции.
(9) 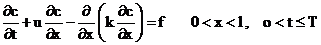 ,
,
(10)  ,
,
(11)  .
.
Предполагается необходимая гладкость функции  и правой части.
и правой части.
Оператор конвективного переноса, что достаточно плохо, не является самосопряженным. Дополнительными усилиями можно добиться его кососимметричности. Этот оператор преобладает над оператором диффузии, т.е. оператор конвективного переноса вносит основной вклад в решение задачи. Таким образом, если приравнять влияние диффузии к нулю, то решение при дополнительных усилиях не сильно изменится.
Математически такие задачи называются сингулярно –возмущенными и и имеют вид:  .
.
Таким образом, плохие качества оператора конвективного переноса в случае преобладания конвекции над диффузией и несамосопряженности оператора конвективного переноса, обуславливаются наличием пограничного слоя в решении задачи.
Построим временную сетку  .
.
На каждом временном интервале будем последовательно решать две задачи.
(12)  ,
,
(13) 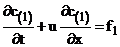 ,
,
(14) 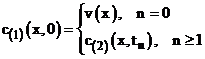
(15) 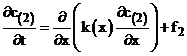 ,
,
(16) 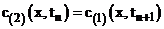 .
.
Дискретизация применяется к каждой из задач таким образом, чтобы на временной сетке для каждого фиксированного времени получалась СЛАУ со знакоопределенной матрицей.
 .
.
Записанная аппроксимация обладает порядком точности  .
.
Задача (15) дискретизируется стандартным образом, как уравнение теплопроводности.
1.7.9. Понятие о монотонных схемах
Формально монотонными схемами называются схемы которые могут быть записаны в канонической форме сеточного уравнения общего вида из исходного семейства.

(1) 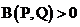 ,
,  .
.
С арифметической точки зрения, принадлежность схемы к исходному семейству приводит к монотонному профилю решения.
График может быть пилообразным, т.е. модель показывает рябь. При нарушении условий (1) возникает пилообразные профили решения ничего общего не имеющие с настоящим решением задачи. Выполнение неравенств (1) добиваются, в частности, искусственными способами, например, введением членов с наиболее высоким порядком и малыми коэффициентами.



 , если все значения
, если все значения  известны, есть величина
известны, есть величина  арифметических операций.
арифметических операций.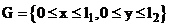 требуется найти решение уравнения:
требуется найти решение уравнения: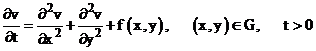 ,
,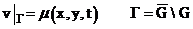
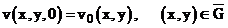 .
. .
. покроем равномерной сеткой с шагами
покроем равномерной сеткой с шагами  по оси Ох и
по оси Ох и  по оси Оу.
по оси Оу. ,
, ,
, .
. .
. ,
,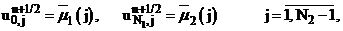
 ,
, ,
, .
.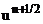 . Если все
. Если все  известны, то система (4) может быть решена методом прогонки. Данный метод является экономичным
известны, то система (4) может быть решена методом прогонки. Данный метод является экономичным  операций. Прогонки выполняются вдоль строк. Если все
операций. Прогонки выполняются вдоль строк. Если все 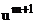 , задача которая также представляет собой систему трех точечных уравнений, заканчивая цикл вычислений к переходу на
, задача которая также представляет собой систему трех точечных уравнений, заканчивая цикл вычислений к переходу на  временной слой. Затраты на арифметические операции составят
временной слой. Затраты на арифметические операции составят  , прогонки выполняются вдоль столбцов. Тогда общее число операций составит порядка
, прогонки выполняются вдоль столбцов. Тогда общее число операций составит порядка 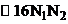 операций.
операций. .
.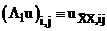 ,
,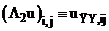 .
.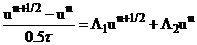 ,
,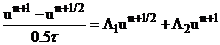 .
.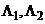 в гильбертовом пространстве сеточных функций определенных на сетке
в гильбертовом пространстве сеточных функций определенных на сетке 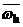 и обращающихся в ноль в узлах
и обращающихся в ноль в узлах 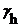 являются самосопряженными, и отрицательно определенными, т.е.
являются самосопряженными, и отрицательно определенными, т.е.  .
. .
. должна быть односвязной областью ступенчатой формы, границы которой являются отрезками прямых параллельных координатным осям. Также накладываются ограничения на тип граничных условий. Для граничных условий 3-го рода коммутативность не выполняется.
должна быть односвязной областью ступенчатой формы, границы которой являются отрезками прямых параллельных координатным осям. Также накладываются ограничения на тип граничных условий. Для граничных условий 3-го рода коммутативность не выполняется.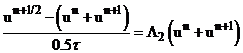 , выразим
, выразим 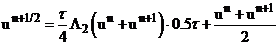 .
. , тогда
, тогда .
.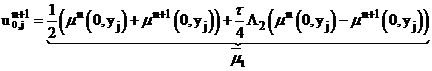
 .
.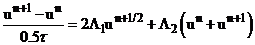 , подставим (9) – выраженное ранее
, подставим (9) – выраженное ранее 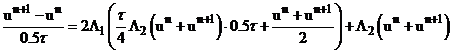 ,
, ,
,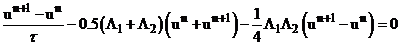 .
.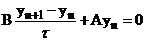 .
. ,
,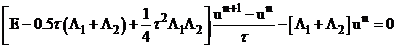 .
.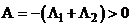 ,
,  ,
, 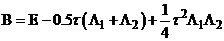 ,
, 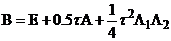 .
. .
. , т.к.
, т.к. 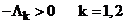 , то
, то  .
. , то
, то  неравенство выполняется. Следовательно, схема параллельных направлений устойчива в энергетическом пространстве
неравенство выполняется. Следовательно, схема параллельных направлений устойчива в энергетическом пространстве  , где
, где 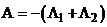 .
. , а только положительноопределенность оператора
, а только положительноопределенность оператора 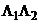 , однако это можно требовать при выполнении коммутативности этих операторов.
, однако это можно требовать при выполнении коммутативности этих операторов. произвольный вектор из
произвольный вектор из 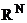 ,
,  - некоторые действительные числа.
- некоторые действительные числа.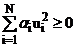 необходимо и достаточно чтобы все
необходимо и достаточно чтобы все 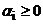 .
. можно представить в виде произведения операторов. Слагаемое
можно представить в виде произведения операторов. Слагаемое  поправляет некорректность задачи.
поправляет некорректность задачи.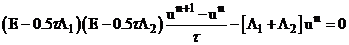
 .
. .
. должны удовлетворять условиям:
должны удовлетворять условиям: 
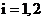 ,
, 
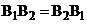 , тогда можно будет применять теорему 1.
, тогда можно будет применять теорему 1. при
при 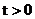 .
. ,
,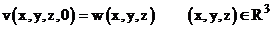 ,
,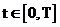 ,рассмотрим вспомогательную сетку
,рассмотрим вспомогательную сетку  наряду с основной.
наряду с основной. :
: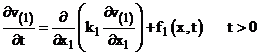 ;
;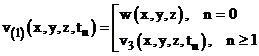
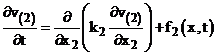 ;
; ;
; ;
; .
. операций.
операций.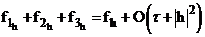 ,
, .
. дискретный аналог задачи (1).
дискретный аналог задачи (1).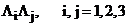 .
. отличается в некоторой норме для
отличается в некоторой норме для  на величину
на величину  .
.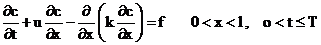 ,
, ,
, .
. и правой части.
и правой части. .
. .
. ,
,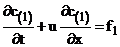 ,
,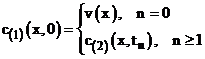
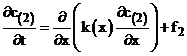 ,
,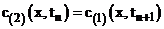 .
. .
. .
.
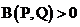 ,
,  .
.


