

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В ряде задач возникает проблема расчета на длительные времена. В таких случаях применение явных схем не целесообразно, т.к. выполнение расчетов на большом числе временных слоев как правило приводит к накоплению погрешности на временных шагах. Использование неявных схем теоретически позволит выбрать любой шаг по времени. Практически этот шаг не может быть слишком большим, например, не следует для уравнений параболического типа выбирать временной шаг больше чем 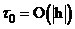 . Одна из рекомендаций состоит в том, чтобы ориентироваться на условие Куранта
. Одна из рекомендаций состоит в том, чтобы ориентироваться на условие Куранта  , если решается задача диффузии – конвекции, где
, если решается задача диффузии – конвекции, где 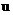 - скорость распространения.
- скорость распространения.
Понятие о трехслойных разностных схемах.
Трехслойные разностные схемы появляются в случае дискретизации начально-краевых задач уравнений гиперболического типа.
Рассмотрим общий вид трехслойных схем.
(1)  ,
,
операторы 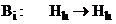 , оператор
, оператор  имеет обратный.
имеет обратный.
Начальные условия:
(2) 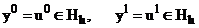
Общий вид трехслойных разностных схем задается формулами (1) и(2).
Для исследования устойчивости (1), (2) по начальным данным трехслойную схему удобно записать в канонической форме трехслойных разностных схем.
Запись (1), (2) означает, что введены сетки по пространству, а также временная сетка  .
.
Будем использовать разностные производные:
(3) 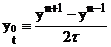 ,
, 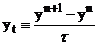 ,
,  ,
, 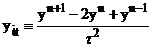 .
.
(4)  ,
,
(5) 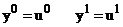 .
.
Операторы 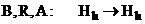 .
.
Покажем, что от общей формы (1) можно перейти к канонической форме (4). Заметим, что справедливы следующие тождества.
(6)  ,
,
(7)  .
.
Подставим (3) в (6) и (7).
(8) 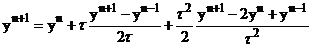 ,
,
(9)  .
.
Если привести подобные члены, то получим доказательство тождеств (6) и (7).
Подставив соотношения (6) и (7) в (1), мы покажем, что из (1) вытекает (4).
|
|
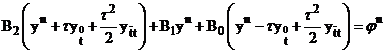 ,
,
 .
.
Сравнивая последнее равенство с канонической формой (4), получаем:
(10) 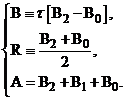
Схему (4), (5) можно преобразовать к двухслойной схеме, записанной в форме:
(11)  ,
,
(12)  .
.
Операторы  .
.
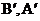 являются операторными матрицами размерности
являются операторными матрицами размерности 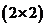 , элементами которых являются операторы, сконструированные из операторов канонической формы (4).
, элементами которых являются операторы, сконструированные из операторов канонической формы (4).
Как обычно в пространстве  вводятся линейные операции над векторами: сложение векторов, умножение векторов на число.
вводятся линейные операции над векторами: сложение векторов, умножение векторов на число.
 , причем матрица
, причем матрица 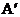 имеет диагональную форму.
имеет диагональную форму.
__________________________________________________________
‼ Определить в явном виде элементы 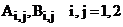 , если
, если 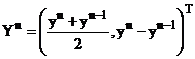 .
.
__________________________________________________________
Схемы (11), (12) при определенных ограничениях на операторы 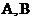 позволяют получить необходимые и достаточные условия устойчивости по начальным данным в
позволяют получить необходимые и достаточные условия устойчивости по начальным данным в 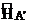 .
.
Достаточное условие:
(13) 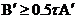 .
.
Операторное неравенство (13) конкретизируется, если определена структура операторов 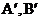 .
.
Приведем без доказательства теорему, которая дает конструктивные ограничения на операторы 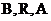 гарантирующие устойчивость по начальным данным. Доказательство теоремы получается естественным образом после определения структуры операторов
гарантирующие устойчивость по начальным данным. Доказательство теоремы получается естественным образом после определения структуры операторов 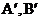 и применения неравенства (13).
и применения неравенства (13).
Теорема 3
Для устойчивости трехслойной схемы (4), (5) по начальным данным достаточно выполнение:
1. 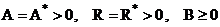 ,
,
2. 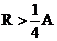 .
.
При этом справедлива оценка 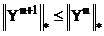 , где
, где  - какая-то норма в
- какая-то норма в  .
.
Пример 1.
Исследовать устойчивость трехслойной схемы с весами.

1). Преобразуем к канонической форме (4).
 ,
,
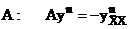 ,
,
 ,
,
 ,
,
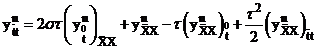 ,
,
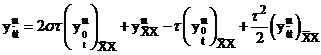 ,
,
 .
.
 ,
, 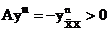 ,
,
 .
.
2). Проверим операторные неравенства.
Выберем такие значения параметров 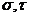 , при которых условия теоремы 3 выполняются.
, при которых условия теоремы 3 выполняются.
1.  .
.
2.  .
.
Проверим 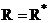 ,
, 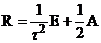 .
.
 ,
,
3. Поверим выполнение 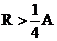 .
.
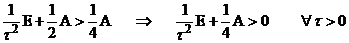 .
.
Итак, все неравенства выполняются, следовательно,схема устойчива.
Пример 2.
Исследовать устойчивость трехслойной схемы.
 .
.
Воспользуемся тождествами (6) и (7).
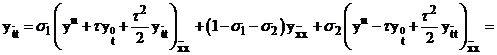

 ,
,  ,
,
Проверим выполнение неравенств достаточных для устойчивости схемы.
1). 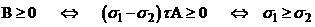 .
.
2).  , что было доказано ранее.
, что было доказано ранее.
|
|
3). 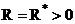 ,
,  .
.
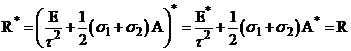 .
.
Так как 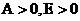 , то
, то  .
.
Рассмотрим два случая:
1. 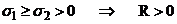 ,
,
2. 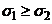 и их знаки произвольны, следовательно,
и их знаки произвольны, следовательно,  .
.
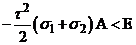 ,
,
 ,
,
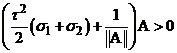 , следовательно,
, следовательно, 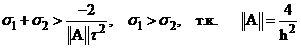 , то
, то 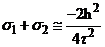 .
.
3. Проверим выполнение неравенства 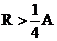 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Итак, получаем ограничения на итерационные параметры:  .
.
Замечание.
Если взять 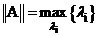 , то получим,
, то получим, 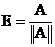 .
.
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!