Лекция 8. Проверка статистических гипотез. Критерий согласия Пирсона

Статистической называется гипотеза о виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) гипотезой 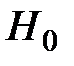 называется выдвинутая гипотеза. Конкурирующей (альтернативной) называется гипотеза , которая противоречит нулевой.

Пример 1. Если 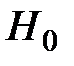 состоит в том, что математическое ожидание  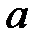нормального распределения равно 100, то конкурирующая гипотеза может иметь вид: , , , .

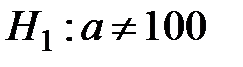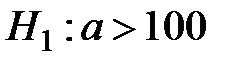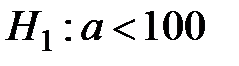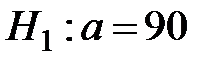В результате проверки статистической гипотезы может быть: 1) принята гипотеза 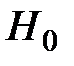; 2) отвергнута гипотеза  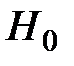(то есть принята альтернативная ей гипотеза ).

При этом могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута гипотеза 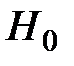, тогда как на самом деле она верна. Ошибка второго рода состоит в том, что будет принята 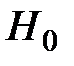, тогда как на самом деле она неверна.

Вероятность совершить ошибку первого рода называется уровнем значимости и обозначается 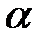. Чаще всего принимают  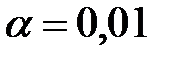или 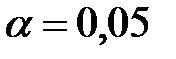. Вероятность ошибки второго рода обозначается .

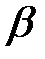Правильное решение также может быть принято в двух случаях:

1) гипотеза 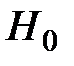 принимается, причем и в действительности она верна (вероятность этого  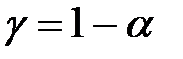называется уровнем доверия);

2) гипотеза 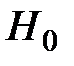 отвергается, причем и в действительности она неверна (вероятность этого  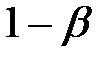называется мощностью критерия).

Статистическим критерием называется случайная величина 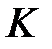, которая служит для проверки гипотезы .

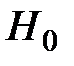По имеющимся данным выборки находят наблюдаемое значение критерия .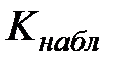

Множество всех возможных значений критерия разбивают на два непересекающихся подмножества: критическую область и областьпринятия гипотезы, которые отделяются друг от друга критическими точками 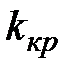. Для каждого конкретного критерия существуют таблицы, по которым находятся критические точки.

Основной принцип проверки статистической гипотезы: если 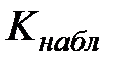 принадлежит критической области, то гипотезу  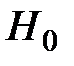отвергают; если  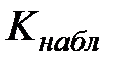принадлежит области принятия гипотезы, то гипотезу  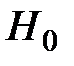принимают.

Принятие нулевой гипотезы не означает, что она доказана. Это означает, что при заданном уровне доверия 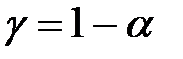 она не противоречит имеющимся данным выборки. На практике для большей уверенности гипотезу проверяют другими способами или повторяют эксперимент, увеличив объем выборки.

Одной из главных задач математической статистики является установление истинного закона распределения генеральной совокупности на основании данных выборки. Предположение о виде этого закона может быть основано на результатах предварительной обработки данных выборки, на аналогии с проведенными ранее исследованиями или на теоретических предпосылках. Например, если в результате предварительной обработки данных выборки была построена гистограмма частот или полигон частот, и их форма напоминает нормальную кривую, то есть основания полагать, что генеральная совокупность имеет нормальный закон распределения.

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Одним из критериев согласия является критерий К. Пирсона или 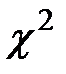 («хи квадрат»). Его сущность состоит в сравнении эмпирических (наблюдаемых) и теоретических (вычисленных в предположении конкретного закона распределения) частот.

Рассмотрим применение критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.

Пусть эмпирическое распределение выборки объема 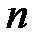 задано в виде последовательности интервалов одинаковой длины и соответствующих им частот:

			…
			…

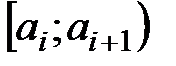
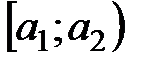
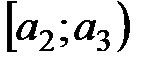
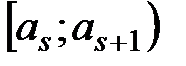
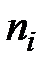
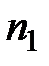
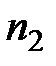
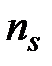
Требуется проверить при уровне значимости 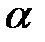 нулевую гипотезу 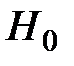: генеральная совокупность  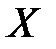распределена нормально.

В качестве критерия проверки гипотезы 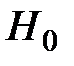 принимается случайная величина , где 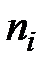 - эмпирические частоты,  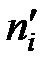- теоретические частоты, 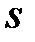- число групп (частичных интервалов) выборки.

Очевидно, что чем меньше различаются 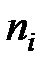 и 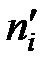, тем меньше величина критерия 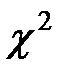, то есть критерий характеризует близость эмпирических и теоретических распределений.

Для того чтобы при заданном уровне значимости 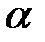 проверить гипотезу 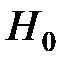, необходимо:

1) Вычислить выборочную среднюю 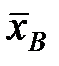и выборочное среднее квадратическое отклонение 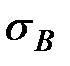, приняв в качестве вариант  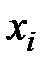середины интервалов .

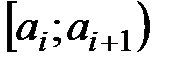2) Нормировать случайную величину 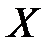, то есть перейти к величине  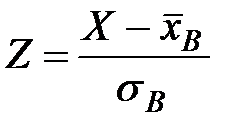и вычислить концы интервалов :

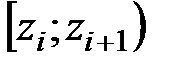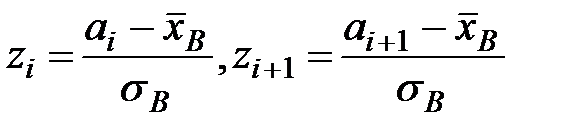, где .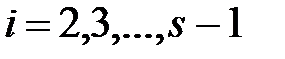

При этом наименьшее значение 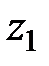 полагают равным 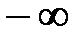, а наибольшее значение  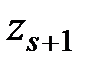полагают равным .

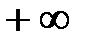3) Вычислить теоретические частоты по формул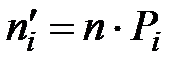е , где

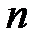– объем выборки,  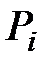– теоретические вероятности попадания случайной величины  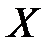в интервалы .

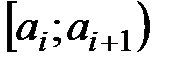При этом 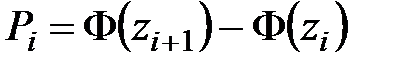, где 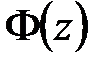 – функция Лапласа, значения которой приведены в специальной таблице (приложение 2).

Для контроля правильности вычислений проверяют выполнение условий: , .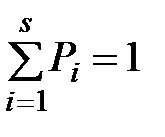

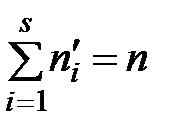4) Найти наблюдаемое значение критерия .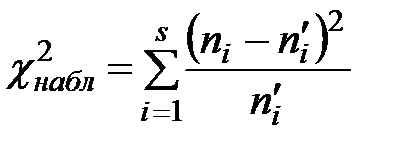

5) По таблице критических точек распределения 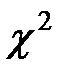(приложение 5), по заданному уровню значимости  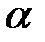и числу степеней свободы  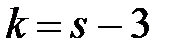найти критическую точку .

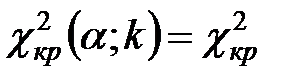6) Если 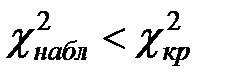, то гипотеза о нормальном распределении генеральной совокупности принимается. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). При этом вероятность того, что принятая гипотеза верна, равна .

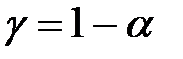Если же 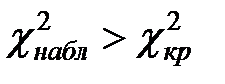, то гипотезу о нормальном распределении отвергают, то есть эмпирические и теоретические частоты различаются значимо (гипотеза не согласуется с экспериментальными данными). Отвергая эту гипотезу, мы совершаем ошибку с вероятностью .

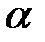Пример 2. При уровне доверия 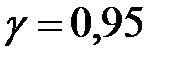 проверить гипотезу о нормальном распределении генеральной совокупности 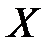, если известно эмпирическое распределение выборки, заданное в виде интервальной таблицы частот (табл. 1). В верхней строке табл. 1 указан номер интервала.

Таблица 1

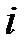
	1	2	3	4	5	6	7
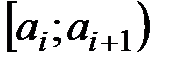
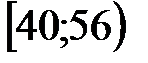
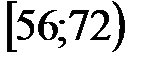
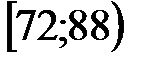
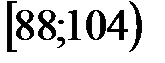
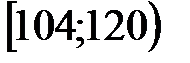
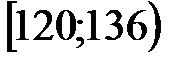
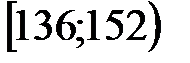
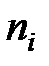
	5	2	10	13	11	6	3

1)В нашем случае 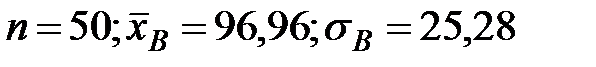 (п. 3.3, пример 2).

2) Найдем интервалы 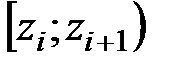. Для этого составим расчетную таблицу (табл. 2).

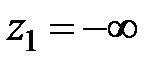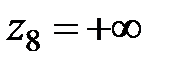При заполнении первого, второго и третьего столбцов табл. 2 используется табл. 1. Числа, стоящие в остальных столбцах табл. 2, вычисляются по указанным формулам, кроме  и . Округление производится до второго знака после запятой.

Таблица 2

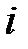
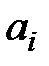
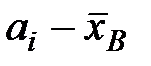
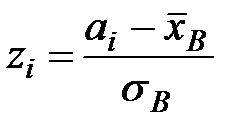
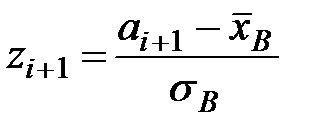
1	40	56	--	-40,96		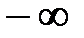-1,62
2	56	72	-40,96	-24,96	-1,62	-0,99
3	72	88	-24,96	-8,96	-0,99	-0,35
4	88	104	-8,96	7,04	-0,35	0,28
5	104	120	7,04	23,04	0,28	0,91
6	120	136	23,04	39,04	0,91	1,54
7	136	152	39,04	--	1,54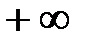

3) Вычислим теоретические частоты 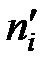. Для этого составим вспомогательную таблицу (табл. 3). Второй и третий столбцы табл. 3 заполняются на основе табл. 2. При заполнении четвертого и пятого столбцов учтем, что функция Лапласа – нечетная, то есть, например, 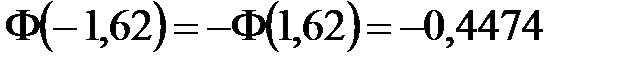. Кроме того, , .

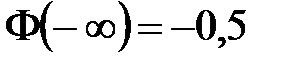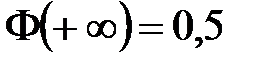Таблица 3

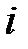
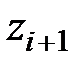
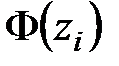
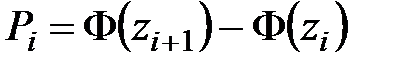
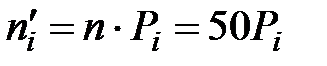
1		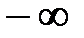-1,62	-0,5000	-0,4474	0,0526	2,630
2	-1,62	-0,99	-0,4474	-0,3389	0,1085	5,425
3	-0,99	-0,35	-0,3389	-0,1368	0,2021	10,105
4	-0,35	0,28	-0,1368	0,1103	0,2471	12,355
5	0,28	0,91	0,1103	0,3186	0,2083	10,415
6	0,91	1,54	0,3186	0,4382	0,1196	5,980
7	1,54		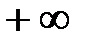0,4382	0,5000	0,0618	3,090
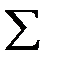
					1	50

Для контроля правильности вычислений следует сложить найденные теоретические вероятности 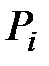 и теоретические частоты 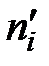. Суммы, записанные в нижней строке таблицы, показывают, что вычисления проведены без ошибок.

    4) Следующая таблица (табл. 4) предназначена для нахождения наблюдаемого значения критерия 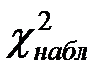. Во втором столбце табл. 4 записаны эмпирические частоты, взятые из табл. 1, а в третьем столбце табл. 4 – теоретические частоты, взятые из табл. 3 и округленные для простоты вычислений до двух знаков после запятой.

Таблица 4

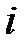
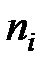
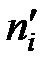
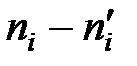
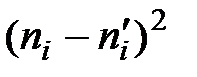
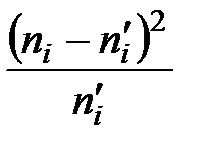
1	5	2,63	2,37	5,6169	2,1357
2	2	5,43	-3,43	11,7649	2,1666
3	10	10,11	-0,11	0,0121	0,0012
4	13	12,36	0,64	0,4096	0,0331
5	11	10,42	0,58	0,3364	0,0323
6	6	5,98	0,02	0,0004	0,0001
7	3	3,09	-0,09	0,0081	0,0026
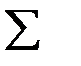
	50	50			4,3716

    Таким образом, .

5) Найдем 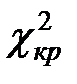. В рассматриваемом примере число интервалов 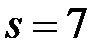, значит число степеней свободы 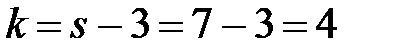. По условию, уровень доверия 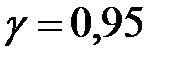, следовательно, уровень значимости 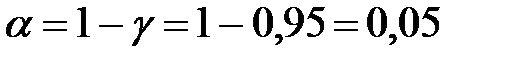. Тогда по таблице критических точек распределения 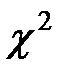находим, что .

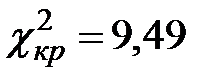6) Так как 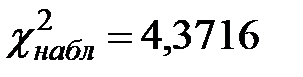, , 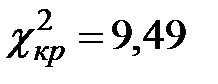то 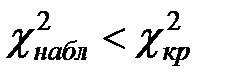. Следовательно, гипотеза о нормальном распределении генеральной совокупности принимается. При этом вероятность того, что принятая нами гипотеза верна, равна заданному числу .

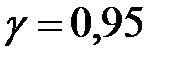Задачи

1. Используя критерий согласия Пирсона, при уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности 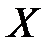, если известно эмпирическое распределение выборки:

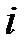
	1	2	3	4	5	6	7	8
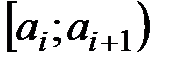
	[2;8)	[8;14)	[14;20)	[20;26)	[26;32)	[32;38)	[38;44)	[44;50)
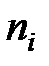
	15	26	25	30	26	21	24	20

2. Используя критерий согласия Пирсона, при уровне доверия 0,99 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности 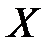 с эмпирическим распределением выборки, приведенным в таблице:

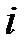
	1	2	3	4	5	6	7	8	9
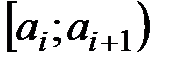
	[1;3)	[3;5)	[5;7)	[7;9)	[9;11)	[11;13)	[13;15)	[15;17)	[17;19)
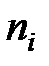
	7	8	15	18	24	19	13	10	6

3. Эмпирическое распределение выборки задано в виде интервальной таблицы частот, содержащей 8 интервалов одинаковой длины. По этому распределению найдено 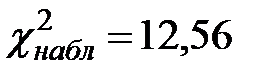. Проверить гипотезу о нормальном распределении генеральной совокупности, если: а) 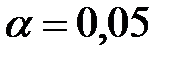; б) .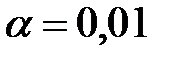

Ответы

1. Гипотеза отвергается. 2. Гипотеза принимается. 3. а) Гипотеза отвергается; б) гипотеза принимается.

 Функциональная, стохастическая и корреляционная зависимость. Выборочный коэффициент корреляции

Две случайные величины  и  могут быть связаны функциональной или стохастической зависимостью, либо быть независимыми.

Зависимость  от  называется функциональной, если каждому значению  соответствует единственное значение .

Зависимость  от  называется стохастической, если каждому значению  соответствует множество значений , причем заранее сказать, какое именно значение примет , нельзя.

В окружающем мире обычно встречается не функциональная, а стохастическая зависимость, так как на случайную величину  влияет не только контролируемый фактор , но и множество других неконтролируемых случайных факторов.

Пусть имеется стохастическая зависимость  от . Если при изменении значения  изменяется среднее значение (условное математическое ожидание) , то зависимость  от  называется корреляционной.

В теории вероятностей под условным математическим ожиданием 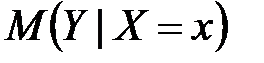 понимается математическое ожидание случайной величины , вычисленное в предположении, что случайная величина  приняла определенное возможное значение, равное .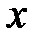

Условное математическое ожидание 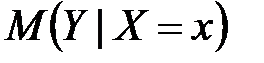 является функцией от 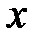. Эту функцию называют функцией регрессии  на . Таким образом, корреляционная зависимость  от  описывается функцией регрессии  на :

.

Пример 1. Пусть  - скорость чтения,  - возраст ребенка. Дети одного возраста , обучающиеся в школе по одинаковой программе, демонстрируют разную скорость чтения , то есть каждому значению  соответствует множество значений . Значит, зависимость  от  не является функциональной, но является стохастической. Это объясняется влиянием на скорость чтения  случайных факторов (дошкольная подготовка, способности ребенка, мастерство учителя и т.п.). Однако при изменении возраста ребенка средняя скорость чтения также изменяется (очевидно, что она возрастает с увеличением возраста), то есть зависимость  от  является корреляционной.

Выявление зависимостей между случайными величинами и количественная оценка этих зависимостей является основной задачей корреляционного анализа – одного из разделов математической статистики.

Для измерения силы линейной зависимости  от  используется коэффициент корреляции .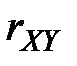

Коэффициент корреляции обладает следующими свойствами:

1. 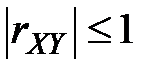 или .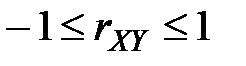

2. .

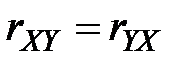3. Если 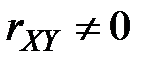, то имеется корреляционная зависимость  от .

4. Если корреляционная зависимость  от  отсутствует, то .

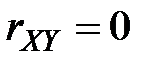5. Если 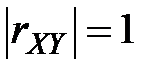, то  и  связаны линейной функциональной зависимостью, и обратно, если  и  связаны линейной функциональной зависимостью, то .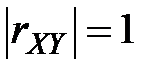

Обратное утверждение для свойства 4 в общем случае неверно, то есть из равенства 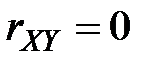 не всегда следует отсутствие корреляционной зависимости  от .

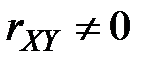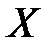Если , то из свойств 2 и 3 следует, что одновременно имеются корреляционные зависимости  от  и  от 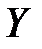, то есть можно говорить о зависимости между  и .

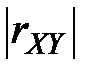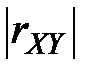Таким образом, чем ближе  к 1, тем ближе стохастическая зависимость между величинами  и  к линейной функциональной. И, наоборот, чем ближе зависимость к линейной функциональной, тем ближе  к 1.

Точечной статистической оценкой коэффициента корреляции 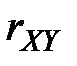 генеральной совокупности (его часто обозначают 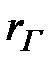) является выборочный коэффициент корреляции 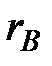. Он находится по формуле:

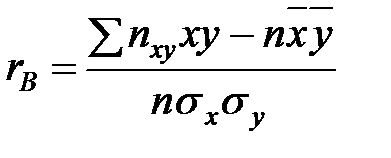, где

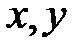 – варианты (наблюдавшиеся значения) случайных величин  и ;  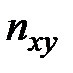– частота пары вариант 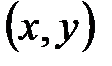;  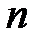– объем выборки;  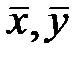– выборочные средние;  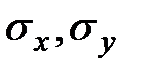– выборочные средние квадратические отклонения.

Выборочный коэффициент корреляции 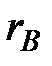 обладает всеми свойствами коэффициента корреляции генеральной совокупности 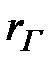, и, следовательно, также характеризует силу линейной зависимости (или, как часто говорят, тесноту линейной связи) между случайными величинами  и .

Для вычисления 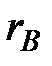 данные наблюдений должны быть сгруппированы и записаны в виде корреляционной таблицы.

Пример 2. Для исследования зависимости годовой выручки 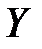 (млн. руб.) от объема капиталовложений  (млн. руб.) получены статистические данные по 100 предприятиям розничной торговли. Найти выборочный коэффициент корреляции и оценить тесноту линейной связи между  и , если статистические данные записаны в виде корреляционной таблицы:

	20	25	30	35	40
16	4	6				10
26		8	10			18
36			32	3	9	44
46			4	12	6	22
56				1	5	6
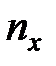
	4	14	46	16	20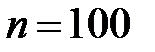

В верхней части корреляционной таблицы записаны наблюдавшиеся значения 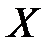, в первом столбце – наблюдавшиеся значения 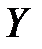. Центральную часть таблицы занимают частоты 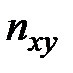. Например, частота 8 означает, что в выборке оказалось восемь предприятий, которые при объеме капиталовложений  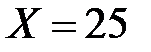получили годовую прибыль 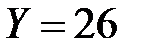. В последней строке и последнем столбце записаны, соответственно, суммы по столбцам и строкам.

Найдем выборочные средние 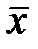 и :

;

.

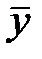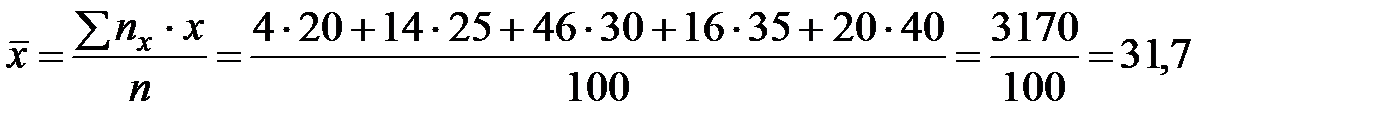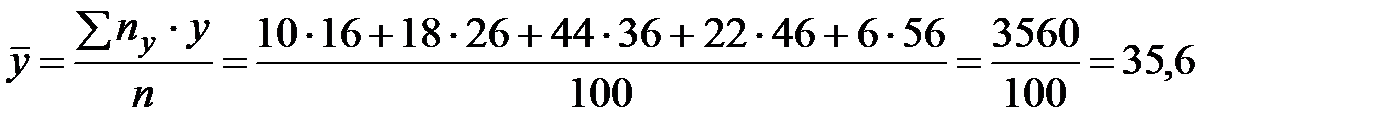Найдем выборочные дисперси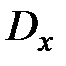и  и :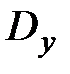

;

.

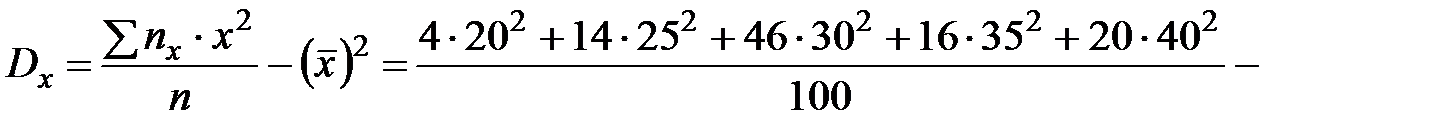
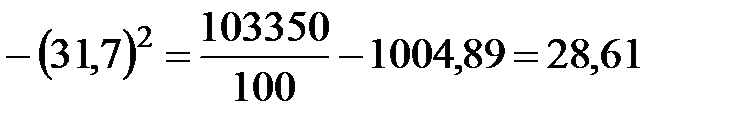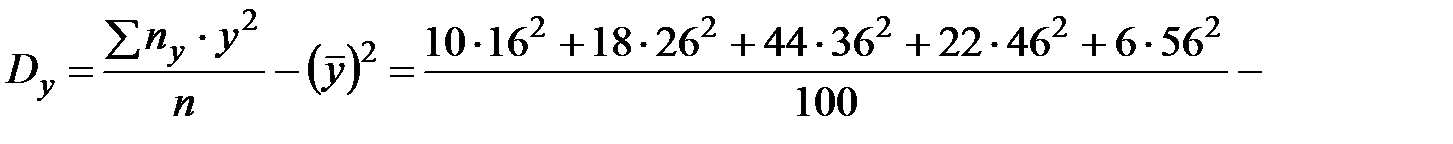
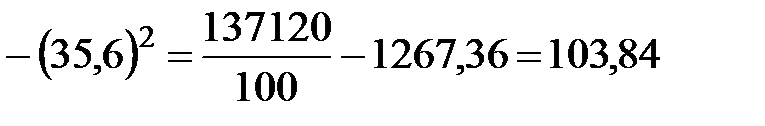Найдем выборочные средние квадратические отклонения :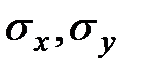

; .

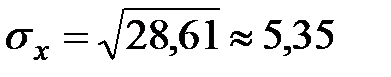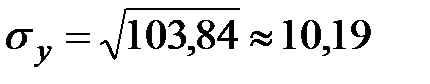Найдем сумму :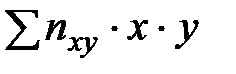

.

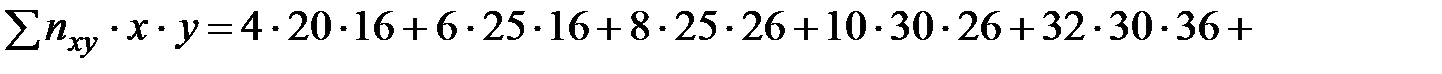
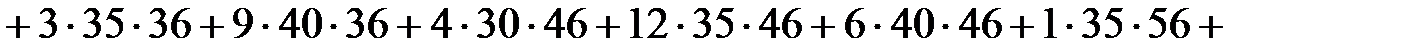
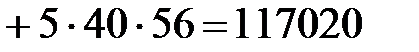Тогда .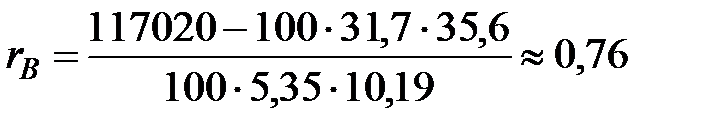

Так как 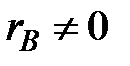, то корреляционная зависимость между  и  имеется. Найденный коэффициент корреляции близок к 1, значит зависимость между  и  достаточно близка к линейной.

Задачи

1. Для исследования зависимости между результатами выполнения учащимися проверочного теста по математике 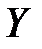 (в баллах) и отметками по математике за год  получены данные, которые приведены в таблице:

 

 

Отметка ()	4	5	3	4	3	3	5	5	4	3	4	3	2
Тест. балл ()	7	10	5	8	6	5	10	8	6	6	9	6	7
Отметка ()	4	3	2	3	5	4	3	3	5	4	3	3	4
Тест. балл ()	8	5	6	5	9	7	6	5	9	10	5	6	8
Отметка ()	5	4	3	3	5	3	5	3	2	3	3	5	2
Тест. балл ()	10	9	5	5	10	6	8	6	5	7	5	10	5
Отметка ()	3	4	2	3	4	3	5	4	3	4	2
Тест. балл ()	6	6	6	5	8	5	10	7	8	8	7

Построить корреляционную таблицу. Найти выборочный коэффициент корреляции и оценить тесноту линейной связи между  и .

2. Для изучения зависимости урожайности сельскохозяйственной культуры от почвенной влаги были исследованы 40 одинаковых участков земли в пойме реки. Результаты представлены в корреляционной таблице, где  – расстояние участка до реки (км),  – урожайность культуры (т/га):

	0,4 – 0,8	0,8 – 1,2	1,2 – 1,6	1,6 – 2,0	2,0 – 2,4
1,5 – 2,5				4	2
2,5 – 3,5			2	6	3
3,5 – 4,5		4	8	1
4,5 – 5,5	4	6

Найти выборочный коэффициент корреляции и оценить тесноту линейной связи между величинами  и .

Указание: Найти середины интервалов и принять их в качестве вариант.

Ответы

1. 0,79. 2. -0,85.