Случайной называется величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
В теории вероятностей рассматривают дискретные и непрерывные случайные величины.
Дискретной называется случайная величина, которая принимает отдельные, изолированные возможные значения (то есть между двумя соседними возможными значениями нет других возможных значений) с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным).
Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число ее возможных значений бесконечно.
Пример 1. Число мальчиков среди 10 новорожденных есть дискретная случайная величина, поскольку она может принимать только значения 0,1,2, …., 9, 10.
Пример 2. Время ожидания автобуса на остановке есть непрерывная случайная величина, так как она может принимать любые значения из промежутка 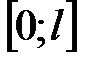 , где
, где  – интервал движения автобусов.
– интервал движения автобусов.
Случайные величины принято обозначать заглавными буквами латинского алфавита  , а их значения – строчными буквами с индексами.
, а их значения – строчными буквами с индексами.
Законом распределения дискретной случайной величины называется соответствие между ее возможными значениями и их вероятностями.
Закон распределения может быть задан таблично, аналитически (то есть с помощью формулы) и графически. В частности, если множество возможных значений дискретной случайной величины  конечно, то ее закон распределения можно задать таблицей вида:
конечно, то ее закон распределения можно задать таблицей вида:
Здесь 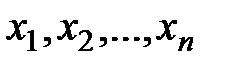 – все возможные значения случайной величины
– все возможные значения случайной величины  , а
, а 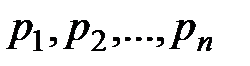 – соответствующие им вероятности.
– соответствующие им вероятности.
При этом  .
.
Пример 3. Монета брошена два раза. Случайная величина  – число выпадений герба. Составить закон распределения
– число выпадений герба. Составить закон распределения  .
.
Дискретная случайная величина  имеет следующие возможные значения:
имеет следующие возможные значения: 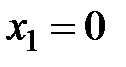 (герб не выпал ни разу),
(герб не выпал ни разу), 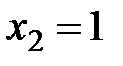 (герб выпал один раз),
(герб выпал один раз), 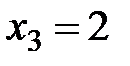 (герб выпал два раза).
(герб выпал два раза).
Найдем вероятность того, что случайная величина  примет значение
примет значение 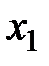 , то есть вероятность события
, то есть вероятность события 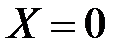 . Поскольку вероятность выпадения герба при каждом подбрасывании монеты одинакова (
. Поскольку вероятность выпадения герба при каждом подбрасывании монеты одинакова ( ) и не зависит от исхода другого подбрасывания, то можно воспользоваться формулой Бернулли:
) и не зависит от исхода другого подбрасывания, то можно воспользоваться формулой Бернулли:
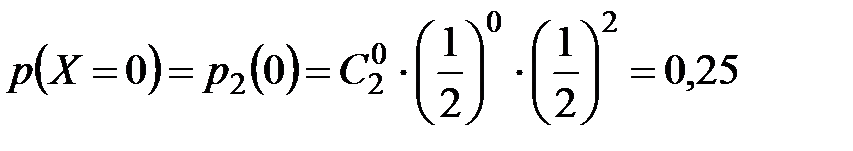 .
.
Рассуждая аналогично, получим:
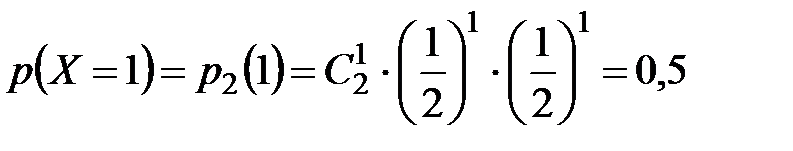 ;
;
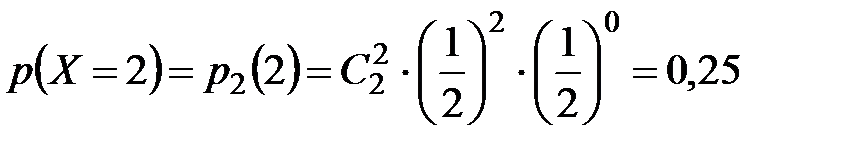 .
.
Закон распределения случайной величины  имеет вид:
имеет вид:
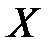
| 0
| 1
| 2
|
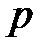
| 0,25
| 0,5
| 0,25
|
Заметим, что 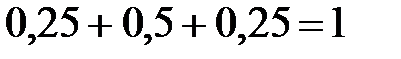 .
.
Биномиальным называется закон распределения дискретной случайной величины  – числа появлений события в
– числа появлений события в 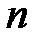 независимых испытаниях, в каждом из которых вероятность появления этого события равна
независимых испытаниях, в каждом из которых вероятность появления этого события равна 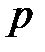 . Случайная величина
. Случайная величина  , распределенная по биномиальному закону, имеет
, распределенная по биномиальному закону, имеет  возможных значений:
возможных значений: 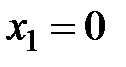 ,
, 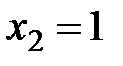 ,
, 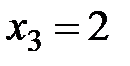 , …,
, …, 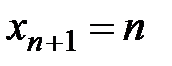 . Вероятности, с которыми
. Вероятности, с которыми  принимает эти значения, вычисляются по формуле Бернулли. В частности, биномиальный закон распределения имеет случайная величина
принимает эти значения, вычисляются по формуле Бернулли. В частности, биномиальный закон распределения имеет случайная величина  – число выпадений герба при двух бросаниях монеты, рассмотренная в примере 3.
– число выпадений герба при двух бросаниях монеты, рассмотренная в примере 3.
Если же для нахождения вероятностей можно использовать формулу Пуассона (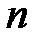 велико, а вероятность
велико, а вероятность 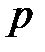 появления события в каждом испытании мала), то говорят, что случайная величина распределена по закону Пуассона.
появления события в каждом испытании мала), то говорят, что случайная величина распределена по закону Пуассона.
При составлении закона распределения дискретной случайной величины, в зависимости от условия задачи, могут использоваться разные способы нахождения вероятностей.
Пример 4. Три стрелка делают по одному выстрелу по учебной цели с разного расстояния. Вероятности их попадания равны, соответственно, 0,3; 0,6; 0,9. Дискретная случайная величина  – число промахов. Составить закон распределения
– число промахов. Составить закон распределения  .
.
Очевидно, что случайная величина  имеет следующие возможные значения:
имеет следующие возможные значения: 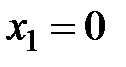 (не произошло ни одного промаха, то есть все стрелки попали в цель),
(не произошло ни одного промаха, то есть все стрелки попали в цель), 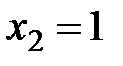 (промахнулся один стрелок),
(промахнулся один стрелок), 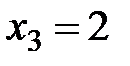 (промахнулись два стрелка),
(промахнулись два стрелка), 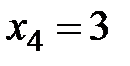 (промахнулись все три стрелка).
(промахнулись все три стрелка).
Используя теоремы сложения и умножения вероятностей (п. 2.4), найдем вероятности того, что случайная величина  примет указанные значения:
примет указанные значения:
 ;
;
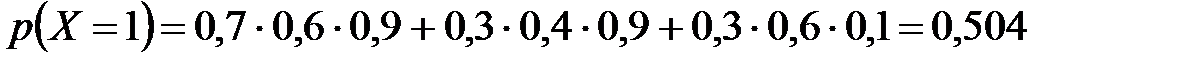 ;
;
 ;
;
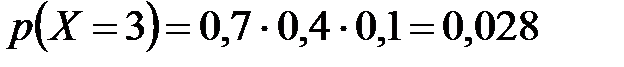 .
.
Закон распределения случайной величины  запишем в виде таблицы:
запишем в виде таблицы:
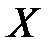
| 0
| 1
| 2
| 3
|
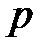
| 0,162
| 0,504
| 0,306
| 0,028
|
Контроль: 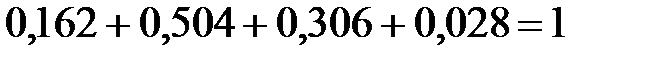 .
.
Пример 5. В урне 10 белых и 2 черных шара. Наудачу извлекаются 5 шаров. Составить закон распределения случайной величины  – числа белых шаров среди извлеченных.
– числа белых шаров среди извлеченных.
Из условия задачи вытекает, что случайная величина может принимать только три значения: 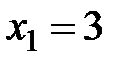 ,
,  ,
,  .
.
Найдем вероятность того, что среди пяти случайным образом извлеченных шаров окажется три белых шара. Воспользуемся классическим определением вероятности. В данном случае общее число элементарных исходов равно числу способов извлечь 5 шаров из 12 имеющихся. Так как порядок извлечения шаров не имеет значения, то 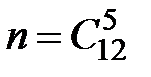 . Число элементарных исходов, благоприятствующих появлению 3 белых шаров, равно
. Число элементарных исходов, благоприятствующих появлению 3 белых шаров, равно  (п. 2.3, пример 2). Значит,
(п. 2.3, пример 2). Значит,
 .
.
Рассуждая аналогично, получим:
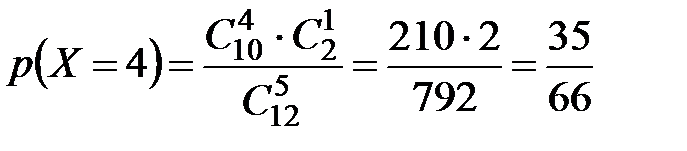 ;
;
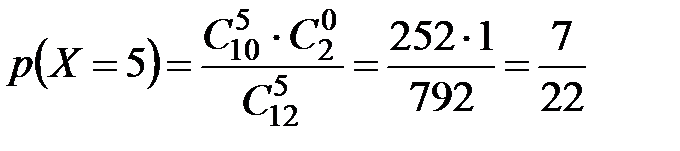 .
.
Закон распределения случайной величины  имеет вид:
имеет вид:
Контроль: 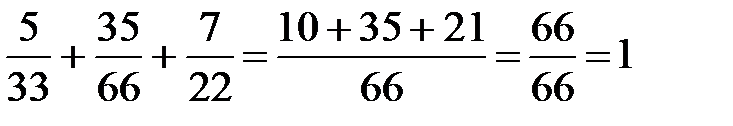 .
.
Пример 6. Вероятность того, что посетитель магазина сделает покупку, равна 0,8. В течение некоторого промежутка времени магазин посетили четыре человека. Составить закон распределения случайной величины  – числа посетителей, сделавших покупку.
– числа посетителей, сделавших покупку.
Очевидно, что случайная величина  распределена по биномиальному закону с параметрами
распределена по биномиальному закону с параметрами 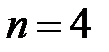 ,
, 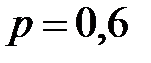 .
.
Возможные значения случайной величины: 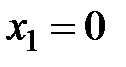 ,
, 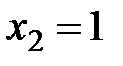 ,
, 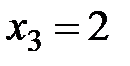 ,
, 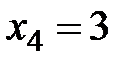 ,
, 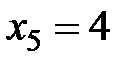 . По формуле Бернулли:
. По формуле Бернулли:
 ;
;
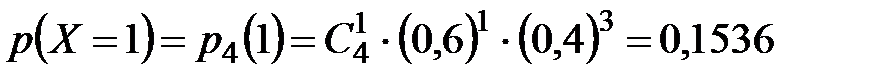 ;
;
 ;
;
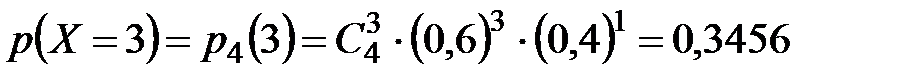 ;
;
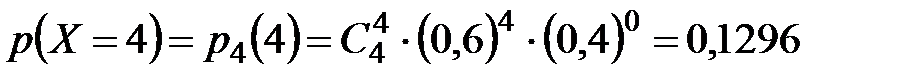 .
.
Закон распределения случайной величины  :
:
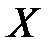
| 0
| 1
| 2
| 3
| 4
|
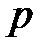
| 0,0256
| 0,1536
| 0,3456
| 0,3456
| 0,1296
|
Контроль: 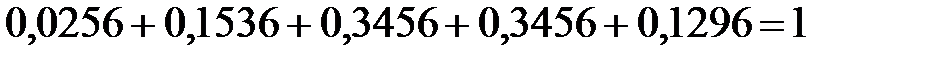 .
.
Задачи
1. В данной местности белые грибы составляют в среднем 20% от общего числа всех съедобных грибов, которые можно найти в лесу. Грибник в течение некоторого промежутка времени нашел 4 съедобных гриба. Составить закон распределения дискретной случайной величины  – числа белых грибов среди найденных.
– числа белых грибов среди найденных.
2. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа не отказавших элементов в одном опыте.
3. Составить закон распределения дискретной случайной величины  – числа мальчиков в семьях с четырьмя детьми (рождение мальчиков и девочек предполагается равновероятным).
– числа мальчиков в семьях с четырьмя детьми (рождение мальчиков и девочек предполагается равновероятным).
4. Три орудия делают по одному выстрелу по учебной цели с разного расстояния. Вероятности их попадания равны, соответственно, 0,4; 0,6; 0,8. Случайная величина  - число попаданий в цель. Составить закон распределения
- число попаданий в цель. Составить закон распределения  .
.
5. Юноша, успешно сдавший ЕГЭ и желающий стать военным летчиком, должен пройти два дополнительных испытания. Вероятность успешного выполнения им заданий первого испытания равна 0,7, второго – 0,4. Случайная величина  - число дополнительных испытаний, не пройденных абитуриентом. Составить закон распределения
- число дополнительных испытаний, не пройденных абитуриентом. Составить закон распределения  .
.
6. В туристическом агентстве работают 10 человек, из них 7 человек владеют иностранными языками. Наудачу выбраны три сотрудника. Составить закон распределения случайной величины  – числа не владеющих иностранными языками сотрудников среди отобранных.
– числа не владеющих иностранными языками сотрудников среди отобранных.
7. В урне 6 белых и 2 черных шара. Наудачу извлекаются 3 шара. Составить закон распределения числа черных шаров среди извлеченных.
Ответы
1.  ;
; 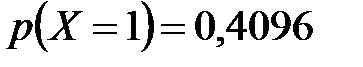 ;
; 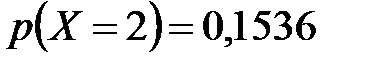 ;
; 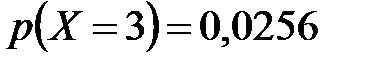 ;
; 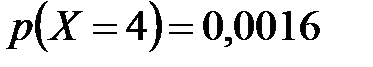 . 2.
. 2.  ;
;  ;
; 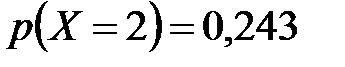 ;
; 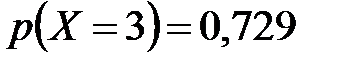 . 3.
. 3. 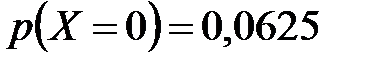 ;
;  ;
; 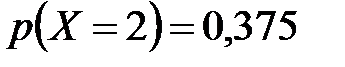 ;
; 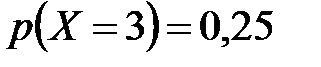 ;
; 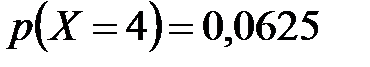 . 4.
. 4.  ;
; 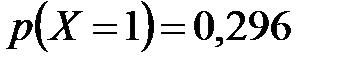 ;
; 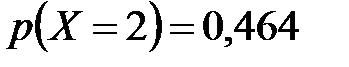 ;
; 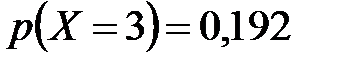 . 5.
. 5.  ;
;  ;
; 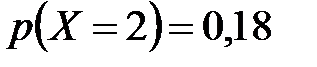 . 6.
. 6. 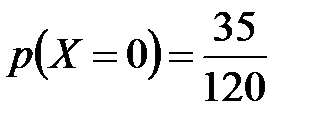 ;
; 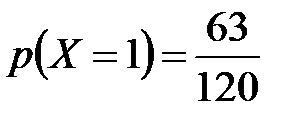 ;
;  ;
; 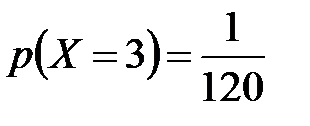 . 7.
. 7. 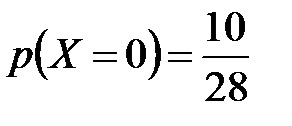 ;
;  ;
; 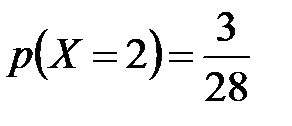 .
.
Числовые характеристики дискретных случайных величин
Математическим ожиданием дискретной случайной величины  называется сумма произведений всех ее возможных значений на их вероятности.
называется сумма произведений всех ее возможных значений на их вероятности.
Если множество возможных значений дискретной случайной величины  конечно, то
конечно, то
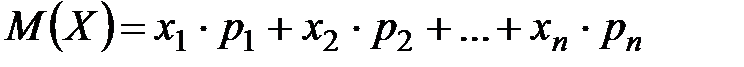 .
.
Пример 1. Найти математическое ожидание дискретной случайной величины  , которая имеет закон распределения:
, которая имеет закон распределения:
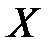
| 2
| 4
| 6
| 8
|
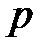
| 0,1
| 0,2
| 0,4
| 0,3
|
По определению математического ожидания
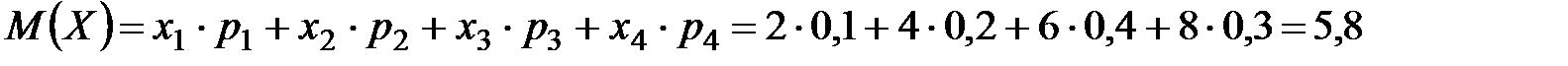 .
.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной: 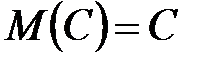 .
.
2. Постоянный множитель можно выносить за знак математического ожидания: 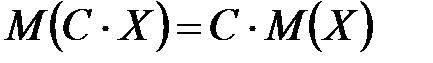 .
.
3. Если случайные величины 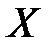 и
и  независимы, то
независимы, то  .
.
4. 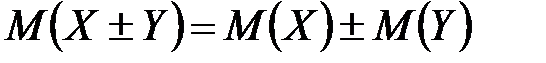 .
.
Пример 2. Найти математическое ожидание случайной величины 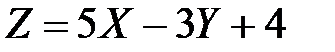 , если известно, что
, если известно, что  ,
, 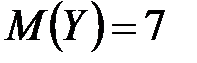 .
.
Используя свойства математического ожидания, получим:
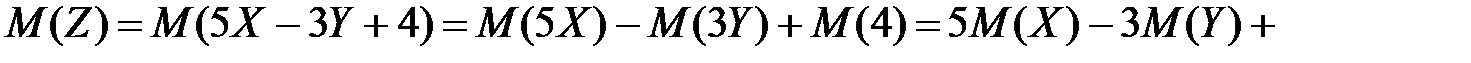
 .
.
Дисперсией случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть
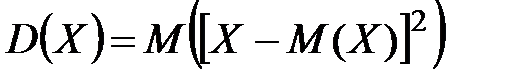 .
.
Для вычисления дисперсии удобно использовать следующую формулу: 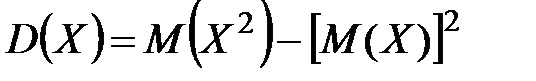 .
.
Пример 3. Найти дисперсию дискретной случайной величины  , которая имеет закон распределения:
, которая имеет закон распределения:
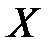
| 2
| 3
| 5
|
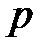
| 0,1
| 0,6
| 0,3
|
Найдем математическое ожидание случайной величины  :
:
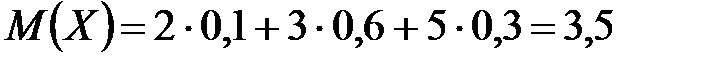 .
.
Напишем закон распределения случайной величины  :
:

| 4
| 9
| 25
|
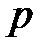
| 0,1
| 0,6
| 0,3
|
Найдем математическое ожидание 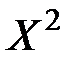 :
:
 .
.
Тогда 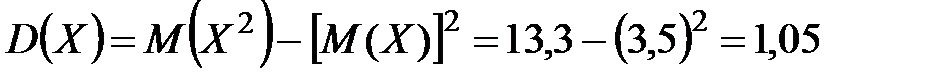 .
.
Дисперсия характеризует степень рассеивания возможных значений случайной величины вокруг ее математического ожидания (среднего значения).
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю: 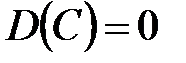 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 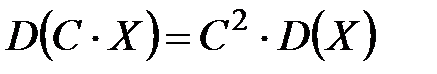 .
.
3. Дисперсия суммы (разности) двух независимых случайных величин равна сумме дисперсий этих величин: 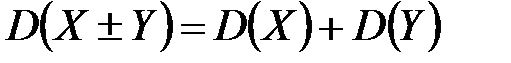 .
.
Средним квадратическим отклонением случайной величины  называется квадратный корень из дисперсии, то есть
называется квадратный корень из дисперсии, то есть
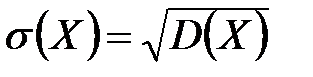 .
.
Величина 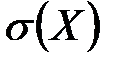 , как и дисперсия, является оценкой степени рассеивания случайной величины
, как и дисперсия, является оценкой степени рассеивания случайной величины  .
.
Пример 4. Случайные величины 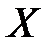 и
и  независимы. Найти среднее квадратическое отклонение случайной величины
независимы. Найти среднее квадратическое отклонение случайной величины 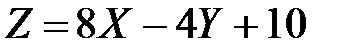 , если известно, что
, если известно, что 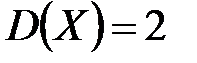 ,
, 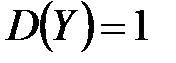 .
.
Используя свойства дисперсии, сначала найдем  :
:
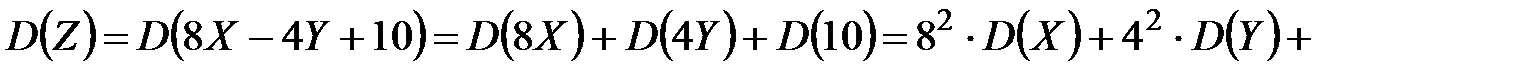
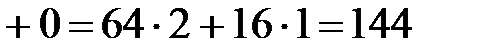 .
.
Значит, 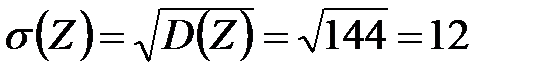 .
.
В некоторых случаях для вычисления математического ожидания и дисперсии можно применять более простые формулы.
Если дискретная случайная величина  распределена по биномиальному закону с параметрами
распределена по биномиальному закону с параметрами  и
и  , то
, то
 ,
, 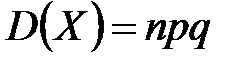 .
.
Пример 5. Вероятность правильного заполнения налоговой декларации налогоплательщиком равна 0,7. Пятнадцать человек независимо друг от друга заполнили налоговые декларации. Найти математическое ожидание и дисперсию случайной величины  – числа правильно заполненных деклараций.
– числа правильно заполненных деклараций.
Нетрудно заметить, что случайная величина  имеет биномиальный закон распределения с параметрами
имеет биномиальный закон распределения с параметрами  и
и 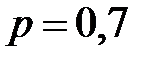 .
.
Следовательно,
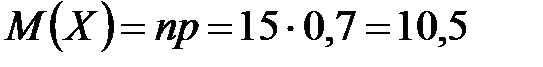 ;
; 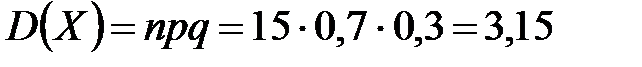 .
.
Задачи
1. Найти математическое ожидание дискретной случайной величины  , имеющей закон распределения:
, имеющей закон распределения:

| 10
| 15
| 20
|

| 0,3
| 0,5
| 0,2
|
2. Найти математическое ожидание дискретной случайной величины  , имеющей закон распределения:
, имеющей закон распределения:

| 1
| 3
| 5
| 7
|
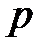
| 0,2
| 0,6
| 0,1
| 0,1
|
3. Найти математическое ожидание случайной величины 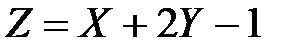 , если
, если  ,
, 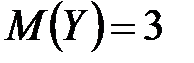 .
.
4. Случайные величины 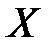 и
и  независимы. Найти математическое ожидание случайной величины
независимы. Найти математическое ожидание случайной величины 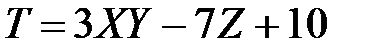 , если известно, что
, если известно, что 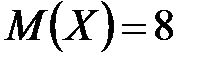 ,
, 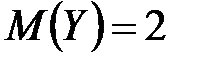 ,
, 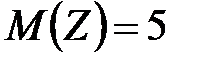 .
.
5. Найти дисперсию дискретной случайной величины  , имеющей закон распределения:
, имеющей закон распределения:

| 4
| 5
| 6
| 7
|
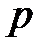
| 0,3
| 0,4
| 0,1
| 0,2
|
6. Найти среднее квадратическое отклонение дискретной случайной величины  ,имеющей закон распределения:
,имеющей закон распределения:

| 3
| 4
| 8
|

| 0,3
| 0,4
| 0,3
|
7. Случайные величины 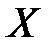 и
и  независимы. Найти дисперсию случайной величины
независимы. Найти дисперсию случайной величины 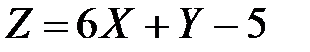 , если известно, что
, если известно, что 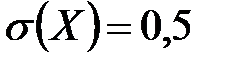 ,
, 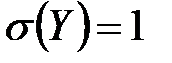 .
.
8. Случайные величины 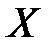 и
и  независимы. Найти среднее квадратическое отклонение случайной величины
независимы. Найти среднее квадратическое отклонение случайной величины  , если известно, что
, если известно, что  ,
, 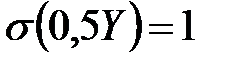 .
.
9. Дискретная случайная величина  принимает три возможных значения:
принимает три возможных значения:  с вероятностью
с вероятностью 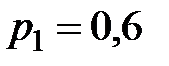 ,
, 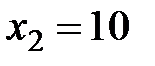 с вероятностью
с вероятностью 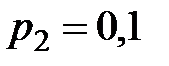 и
и  с вероятностью
с вероятностью 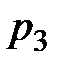 . Найти
. Найти  и
и 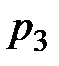 , зная, что
, зная, что 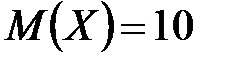 .
.
10. Дискретная случайная величина  принимает два значения:
принимает два значения: 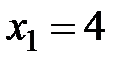 ,
, 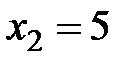 , а ее математическое ожидание равно 4,6. Найти закон распределения
, а ее математическое ожидание равно 4,6. Найти закон распределения  .
.
11. Дискретная случайная величина  принимает значения
принимает значения  и
и  с вероятностями 0,2 и 0,8 соответственно. Математическое ожидание случайной величины
с вероятностями 0,2 и 0,8 соответственно. Математическое ожидание случайной величины  равно 1,3, а ее дисперсия равна 0,16. Найти значения случайной величины
равно 1,3, а ее дисперсия равна 0,16. Найти значения случайной величины  .
.
12. Дискретная случайная величина  принимает три возможных значения:
принимает три возможных значения: 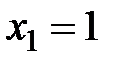 ,
, 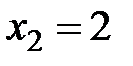 ,
, 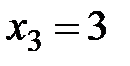 . Известно также, что
. Известно также, что 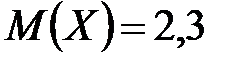 ,
, 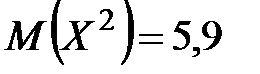 . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  .
.
13. Дискретная случайная величина  имеет только два возможных значения:
имеет только два возможных значения: 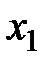 и
и 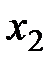 , причем
, причем 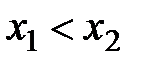 . Вероятность того, что
. Вероятность того, что  примет значение
примет значение 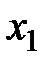 , равна 0,5. Найти закон распределения
, равна 0,5. Найти закон распределения  , если
, если 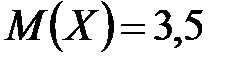 и
и  .
.
14. Бросается игральный кубик. Найти математическое ожидание и дисперсию дискретной случайной величины  , равной числу выпавших очков.
, равной числу выпавших очков.
15. Найти математическое ожидание и среднее квадратическое отклонение дискретной случайной величины  , имеющей биномиальное распределение с параметрами
, имеющей биномиальное распределение с параметрами  и
и  , если: а)
, если: а) 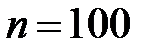 ,
, 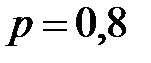 ; б)
; б)  ,
,  .
.
16. Найти математическое ожидание и дисперсию дискретной случайной величины  – числа попаданий в мишень при 20 независимых выстрелах, если вероятность попадания при одном выстреле равна 0,4.
– числа попаданий в мишень при 20 независимых выстрелах, если вероятность попадания при одном выстреле равна 0,4.
17. Вероятность выигрыша по одному лотерейному билету равна 0,15. Найти математическое ожидание и среднее квадратическое отклонение дискретной случайной величины  – числа выигрышных лотерейных билетов из 12 купленных.
– числа выигрышных лотерейных билетов из 12 купленных.
18. Найти дисперсию дискретной случайной величины  – числа появлений события
– числа появлений события 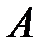 в десяти независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в десяти независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что  .
.
Ответы
1. 14,5. 2. 3,2. 3. 15. 4. 23. 5. 1,16. 6. 2,07. 7. 10. 8. 13,42. 9. 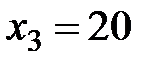 ,
, 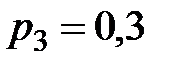 . 10.
. 10.  ;
;  . 11.
. 11. 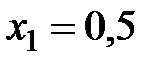 ;
; 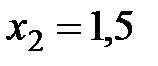 . 12.
. 12.  ;
;  ;
; 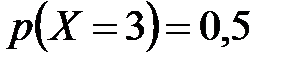 . 13.
. 13. 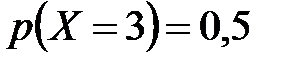 ;
; 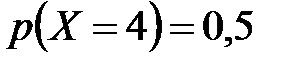 . 14.
. 14. 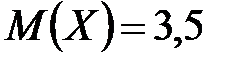 ;
; 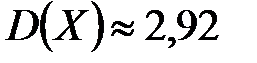 . 15. а)
. 15. а) 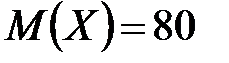 ,
,  ; б)
; б) 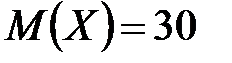 ,
,  . 16.
. 16. 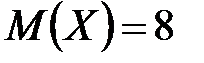 ;
;  . 17.
. 17.  ;
; 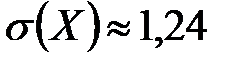 . 18. 2,4.
. 18. 2,4.
Функция распределения вероятностей случайной величины
Функцией распределения случайной величины  называется функция
называется функция 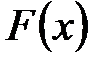 , определяющая для каждого действительного значения
, определяющая для каждого действительного значения 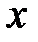 вероятность того, что случайная величина
вероятность того, что случайная величина  в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее 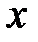 , то есть
, то есть
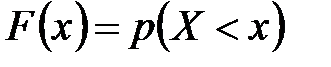 .
.
Свойства функции распределения:
1. Значения функции распределения 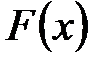 принадлежат отрезку
принадлежат отрезку 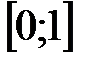 , то есть
, то есть 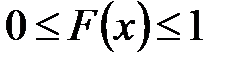 для любого
для любого  .
.
2. Функция распределения 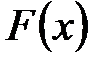 является неубывающей, то есть если
является неубывающей, то есть если 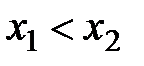 , то
, то 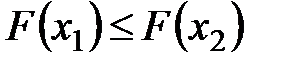 .
.
3. Для функции распределения 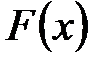 справедливы следующие предельные соотношения:
справедливы следующие предельные соотношения:  ,
, 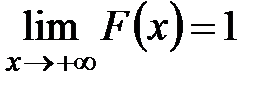 .
.
4. Функция распределения 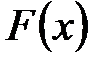 непрерывна слева в каждой точке, то есть
непрерывна слева в каждой точке, то есть 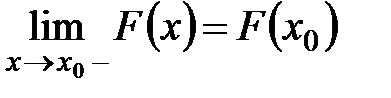 .
.
Справедливы также следующие утверждения:
1. Вероятность того, что случайная величина  примет значение, принадлежащее полуинтервалу
примет значение, принадлежащее полуинтервалу 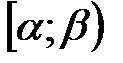 , равна разности значений ее функции распределения
, равна разности значений ее функции распределения 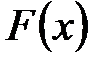 на концах этого полуинтервала:
на концах этого полуинтервала: 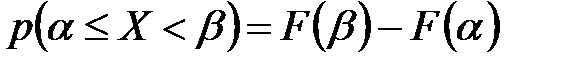 .
.
2. Вероятность того, что непрерывная случайная величина  примет одно определенное значение
примет одно определенное значение 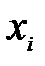 , равна нулю, то есть
, равна нулю, то есть  .
.
Из двух последних утверждений следует, что если  – непрерывная случайная величина, то
– непрерывная случайная величина, то
 .
.
График функции распределения непрерывной случайной величины представляет собой непрерывную кривую. График функции распределения дискретной случайной величины имеет вид разрывной ступенчатой линии.
Пример 1. Дискретная случайная величина 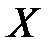 имеет закон распределения:
имеет закон распределения:
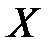
| 3
| 5
| 11
|
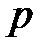
| 0,3
| 0,1
| 0,6
|
Найти функцию распределения случайной величины и построить ее график.
1) Если 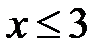 , то
, то 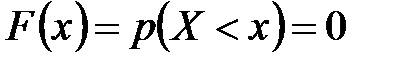 , так как случайная величина
, так как случайная величина  не принимает значений, меньших 3.
не принимает значений, меньших 3.
2) Если 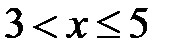 , то
, то  .
.
3) Если 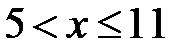 , то
, то 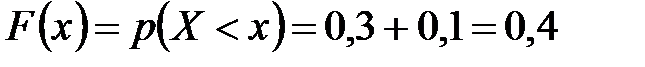 .
.
4) Если  , то
, то  .
.
Таким образом, функция распределения дискретной случайной величины  имеет вид:
имеет вид:

График этой функции изображен на рис. 1.
Рис.1. График функции распределения
Рассмотренный пример иллюстрирует важное свойство функции распределения дискретной случайной величины: точками разрыва функции распределения  являются возможные значения случайной величины
являются возможные значения случайной величины  , причем величина «скачка» в каждой точкеразрыва равна вероятности, с которой случайная величина принимает соответствующее значение.
, причем величина «скачка» в каждой точкеразрыва равна вероятности, с которой случайная величина принимает соответствующее значение.
Пример 2. Дискретная случайная величина  задана функцией распределения:
задана функцией распределения:
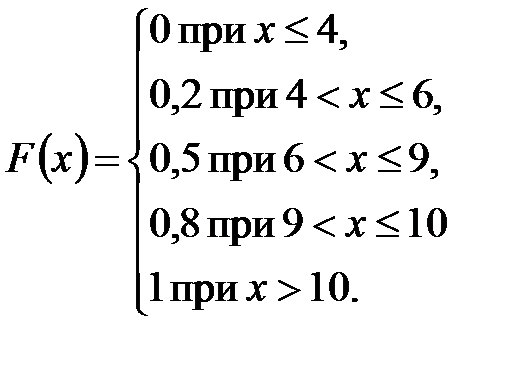
1) Найти закон распределения  .
.
2) Найти следующие вероятности: а) 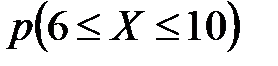 ; б)
; б) 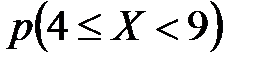 ; в)
; в) 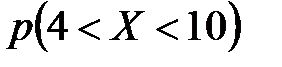 ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
1) В данном случае точками разрыва функции распределения являются точки 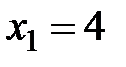 ,
,  ,
, 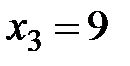 и
и  . Значит, случайная величина
. Значит, случайная величина  имеет четыре возможных значения.
имеет четыре возможных значения.
Величина «скачка» в каждой из перечисленных точек равна вероятности, с которой случайная величина принимает соответствующее значение, поэтому:
 ;
; 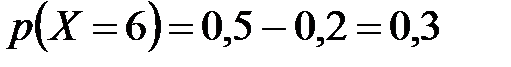 ;
;
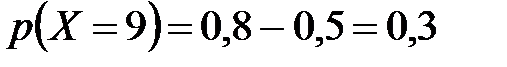 ;
; 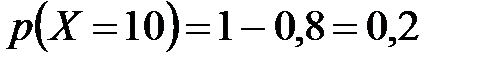 .
.
Таким образом, закон распределения величины  имеет вид:
имеет вид:

| 4
| 6
| 9
| 10
|
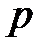
| 0,2
| 0,3
| 0,3
| 0,2
|
2) Найдем вероятности:
а) Так как случайная величина  может принимать только четыре указанных в таблице значения, то событие, состоящее в том, что
может принимать только четыре указанных в таблице значения, то событие, состоящее в том, что 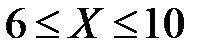 , является суммой следующих несовместных событий:
, является суммой следующих несовместных событий: 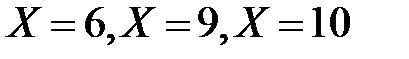 . Тогда по теореме сложения вероятностей
. Тогда по теореме сложения вероятностей
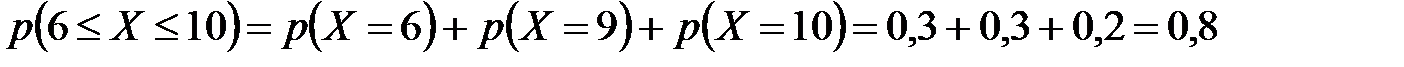 .
.
б) 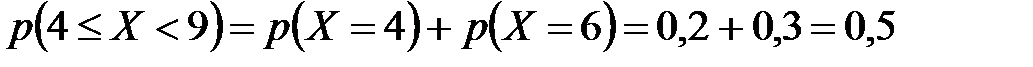 .
.
в)  .
.
г) 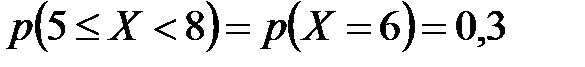 .
.
д) 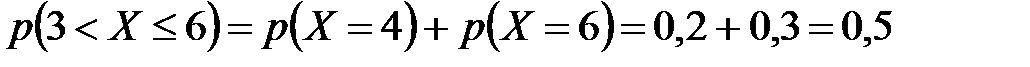 .
.
е) 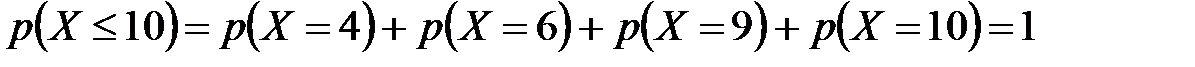 .
.
ж) Поскольку случайная величина  не принимает значений, меньших 4, то
не принимает значений, меньших 4, то 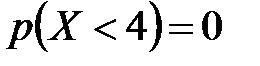 .
.
з)  .
.
В некоторых случаях для вычисления вероятности удобно использовать тот факт, что 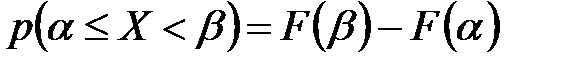 .
.
Например,
 ;
;
 .
.
Задачи
1. Дискретная случайная величина  имеет закон распределения:
имеет закон распределения:

| 3
| 6
| 9
|

| 0,3
| 0,5
| 0,2
|
Найти функцию распределения 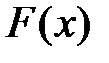 и построить ее график. Найти: а)
и построить ее график. Найти: а)  ; б)
; б) 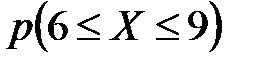 ; в)
; в)  ; г)
; г) 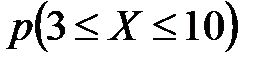 ; д)
; д)  ; е)
; е) 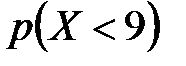 ; ж)
; ж)  ; з)
; з) 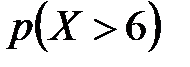 .
.
2. Дискретная случайная величина  имеет закон распределения:
имеет закон распределения:

| 0
| 4
| 7
| 8
|
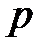
| 0,2
| 0,6
| 0,1
| 0,1
|
Найти функцию распределения 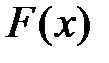 и построить ее график. Найти: а)
и построить ее график. Найти: а) 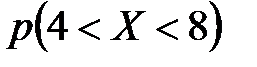 ; б)
; б)  ;
;



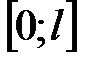 , где
, где  – интервал движения автобусов.
– интервал движения автобусов. , а их значения – строчными буквами с индексами.
, а их значения – строчными буквами с индексами. конечно, то ее закон распределения можно задать таблицей вида:
конечно, то ее закон распределения можно задать таблицей вида: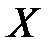
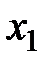
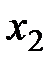

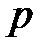
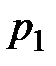
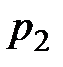
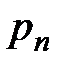
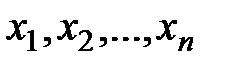 – все возможные значения случайной величины
– все возможные значения случайной величины 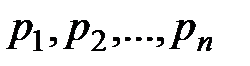 – соответствующие им вероятности.
– соответствующие им вероятности. .
.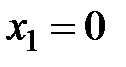 (герб не выпал ни разу),
(герб не выпал ни разу), 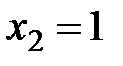 (герб выпал один раз),
(герб выпал один раз), 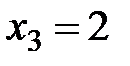 (герб выпал два раза).
(герб выпал два раза).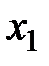 , то есть вероятность события
, то есть вероятность события 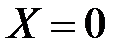 . Поскольку вероятность выпадения герба при каждом подбрасывании монеты одинакова (
. Поскольку вероятность выпадения герба при каждом подбрасывании монеты одинакова ( ) и не зависит от исхода другого подбрасывания, то можно воспользоваться формулой Бернулли:
) и не зависит от исхода другого подбрасывания, то можно воспользоваться формулой Бернулли: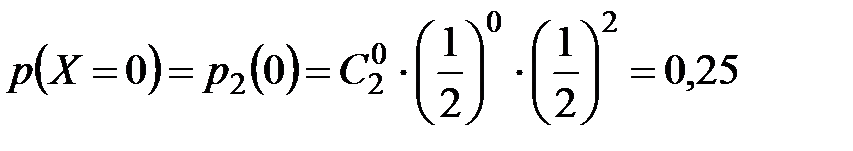 .
.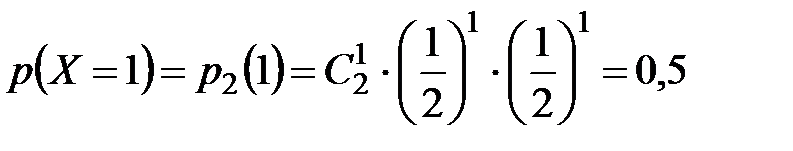 ;
;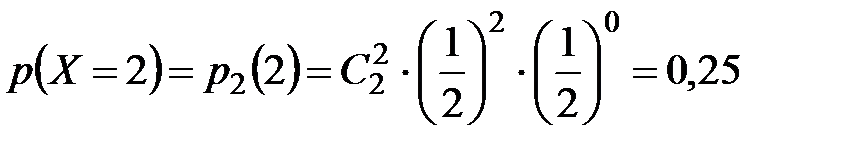 .
.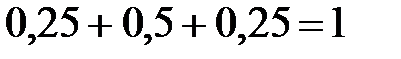 .
.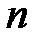 независимых испытаниях, в каждом из которых вероятность появления этого события равна
независимых испытаниях, в каждом из которых вероятность появления этого события равна 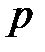 . Случайная величина
. Случайная величина  возможных значений:
возможных значений: 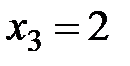 , …,
, …, 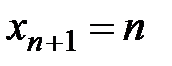 . Вероятности, с которыми
. Вероятности, с которыми 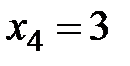 (промахнулись все три стрелка).
(промахнулись все три стрелка). ;
;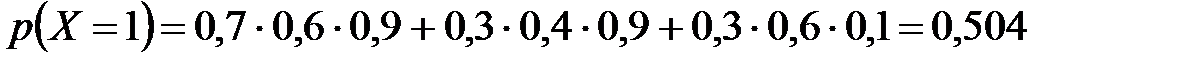 ;
; ;
;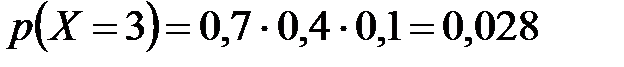 .
.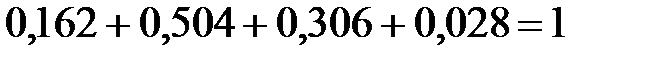 .
.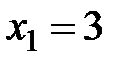 ,
,  ,
,  .
.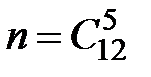 . Число элементарных исходов, благоприятствующих появлению 3 белых шаров, равно
. Число элементарных исходов, благоприятствующих появлению 3 белых шаров, равно  (п. 2.3, пример 2). Значит,
(п. 2.3, пример 2). Значит, .
.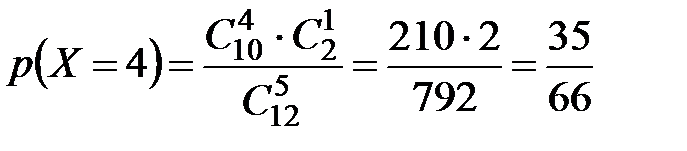 ;
;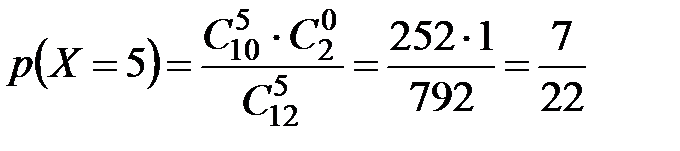 .
.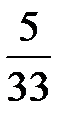
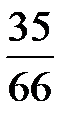
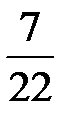
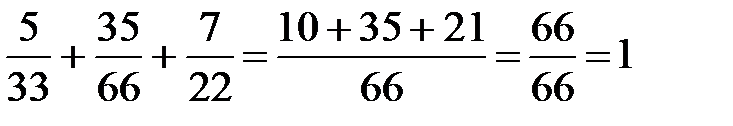 .
.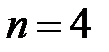 ,
, 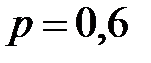 .
.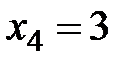 ,
, 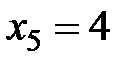 . По формуле Бернулли:
. По формуле Бернулли: ;
;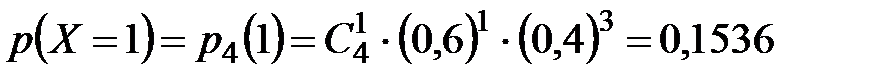 ;
; ;
;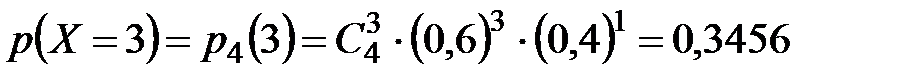 ;
;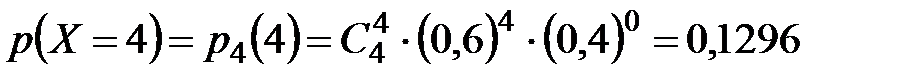 .
.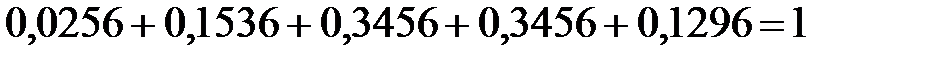 .
. ;
; 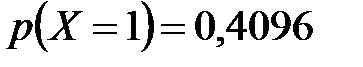 ;
; 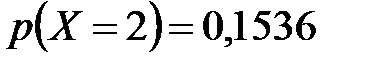 ;
; 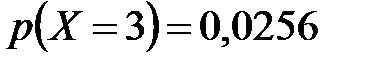 ;
; 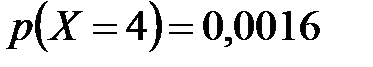 . 2.
. 2.  ;
;  ;
; 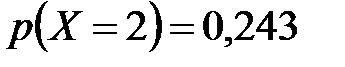 ;
; 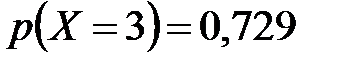 . 3.
. 3. 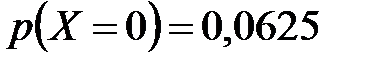 ;
;  ;
; 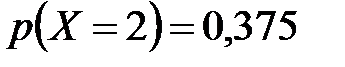 ;
; 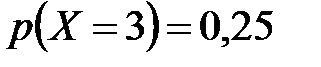 ;
; 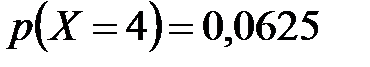 . 4.
. 4.  ;
; 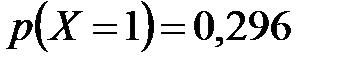 ;
; 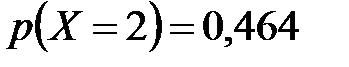 ;
; 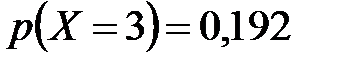 . 5.
. 5.  ;
;  ;
; 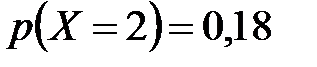 . 6.
. 6. 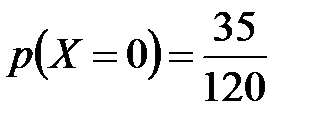 ;
; 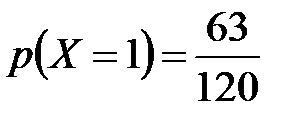 ;
;  ;
; 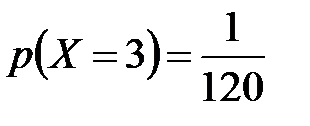 . 7.
. 7. 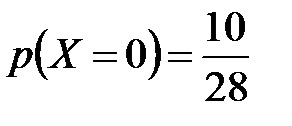 ;
;  ;
; 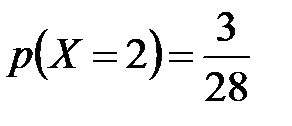 .
.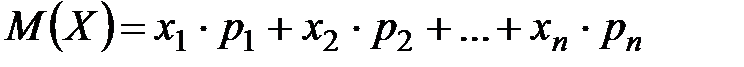 .
.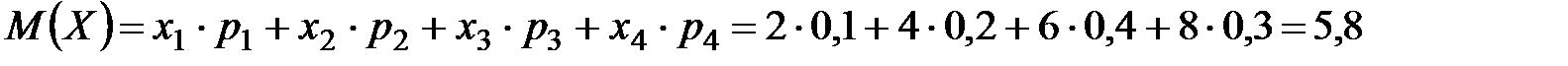 .
.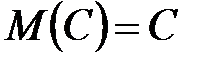 .
.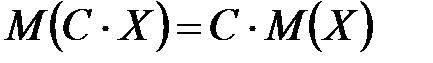 .
.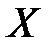 и
и  независимы, то
независимы, то  .
.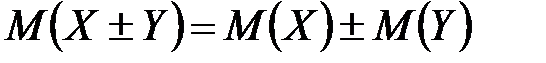 .
.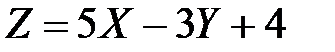 , если известно, что
, если известно, что  ,
, 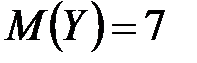 .
.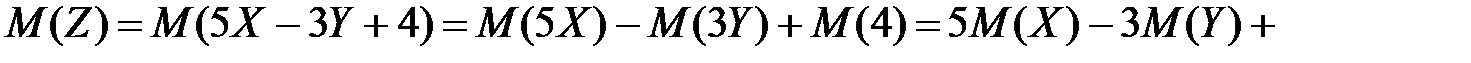
 .
.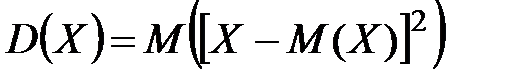 .
.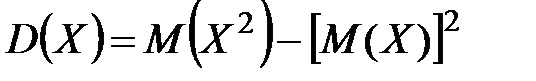 .
.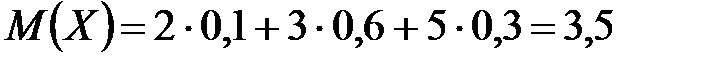 .
. :
:
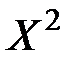 :
: .
.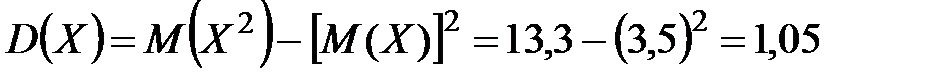 .
.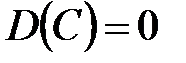 .
.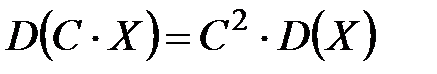 .
.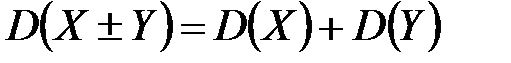 .
.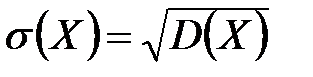 .
.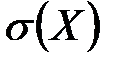 , как и дисперсия, является оценкой степени рассеивания случайной величины
, как и дисперсия, является оценкой степени рассеивания случайной величины 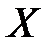 и
и  независимы. Найти среднее квадратическое отклонение случайной величины
независимы. Найти среднее квадратическое отклонение случайной величины 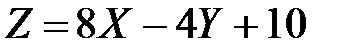 , если известно, что
, если известно, что 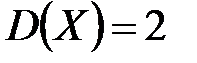 ,
, 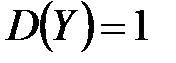 .
.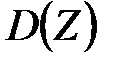 :
: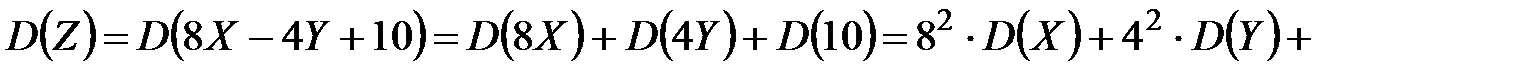
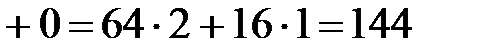 .
.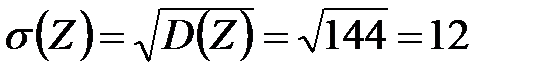 .
. и
и  , то
, то ,
, 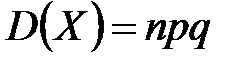 .
. и
и 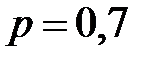 .
.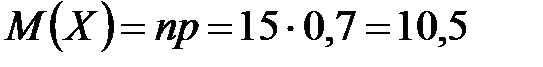 ;
; 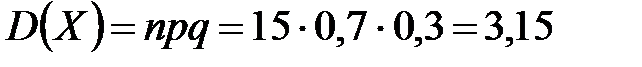 .
.
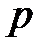
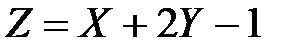 , если
, если  ,
, 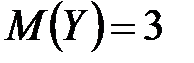 .
.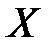 и
и  независимы. Найти математическое ожидание случайной величины
независимы. Найти математическое ожидание случайной величины 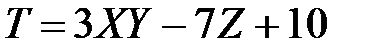 , если известно, что
, если известно, что 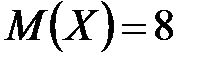 ,
, 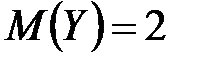 ,
, 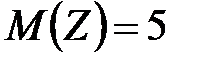 .
.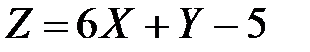 , если известно, что
, если известно, что 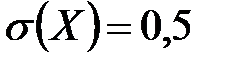 ,
, 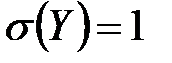 .
. , если известно, что
, если известно, что  ,
, 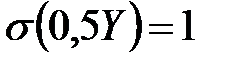 .
. с вероятностью
с вероятностью 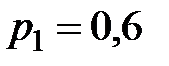 ,
, 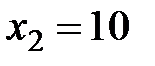 с вероятностью
с вероятностью 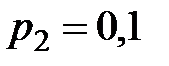 и
и  с вероятностью
с вероятностью 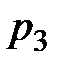 . Найти
. Найти 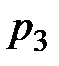 , зная, что
, зная, что 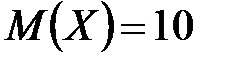 .
.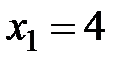 ,
, 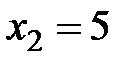 , а ее математическое ожидание равно 4,6. Найти закон распределения
, а ее математическое ожидание равно 4,6. Найти закон распределения  и
и  с вероятностями 0,2 и 0,8 соответственно. Математическое ожидание случайной величины
с вероятностями 0,2 и 0,8 соответственно. Математическое ожидание случайной величины 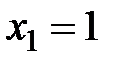 ,
, 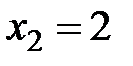 ,
, 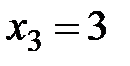 . Известно также, что
. Известно также, что 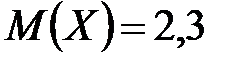 ,
, 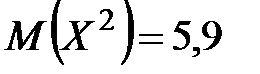 . Найти закон распределения случайной величины
. Найти закон распределения случайной величины 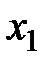 и
и 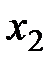 , причем
, причем 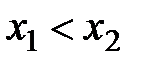 . Вероятность того, что
. Вероятность того, что 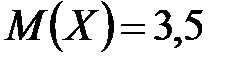 и
и  .
.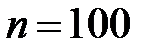 ,
, 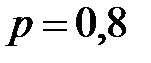 ; б)
; б)  ,
,  .
. в десяти независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в десяти независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что  .
.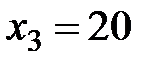 ,
, 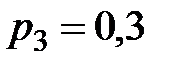 . 10.
. 10.  ;
;  . 11.
. 11. 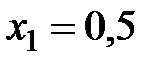 ;
; 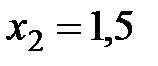 . 12.
. 12.  ;
;  ;
; 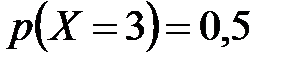 . 13.
. 13. 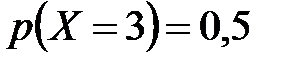 ;
; 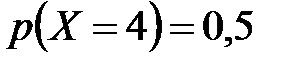 . 14.
. 14. 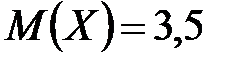 ;
; 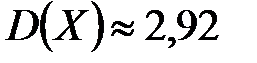 . 15. а)
. 15. а) 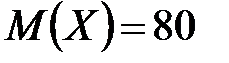 ,
,  ; б)
; б) 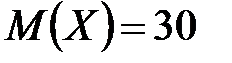 ,
,  . 16.
. 16. 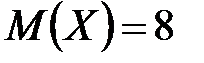 ;
;  . 17.
. 17.  ;
; 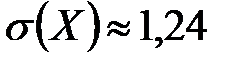 . 18. 2,4.
. 18. 2,4.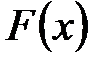 , определяющая для каждого действительного значения
, определяющая для каждого действительного значения 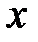 вероятность того, что случайная величина
вероятность того, что случайная величина 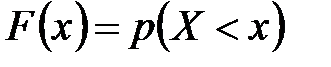 .
.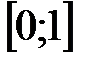 , то есть
, то есть 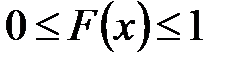 для любого
для любого  .
.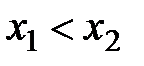 , то
, то 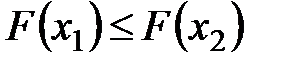 .
. ,
, 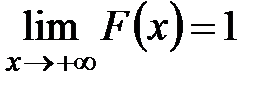 .
.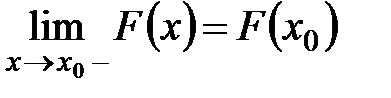 .
. , равна разности значений ее функции распределения
, равна разности значений ее функции распределения 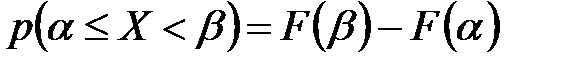 .
.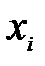 , равна нулю, то есть
, равна нулю, то есть  .
. .
.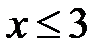 , то
, то 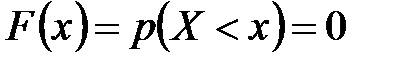 , так как случайная величина
, так как случайная величина 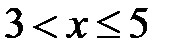 , то
, то  .
.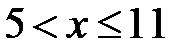 , то
, то 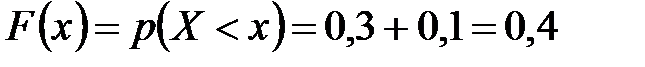 .
. , то
, то  .
.
 являются возможные значения случайной величины
являются возможные значения случайной величины 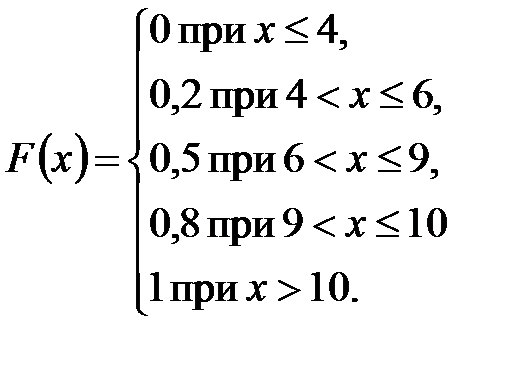
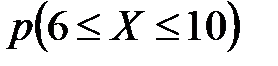 ; б)
; б) 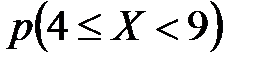 ; в)
; в) 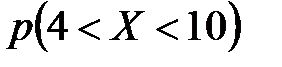 ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.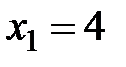 ,
,  ,
, 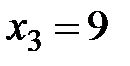 и
и  . Значит, случайная величина
. Значит, случайная величина  ;
; 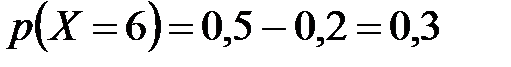 ;
;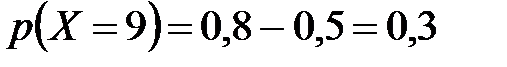 ;
; 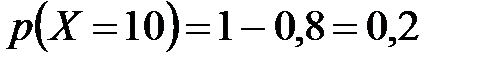 .
.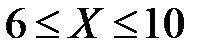 , является суммой следующих несовместных событий:
, является суммой следующих несовместных событий: 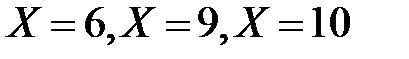 . Тогда по теореме сложения вероятностей
. Тогда по теореме сложения вероятностей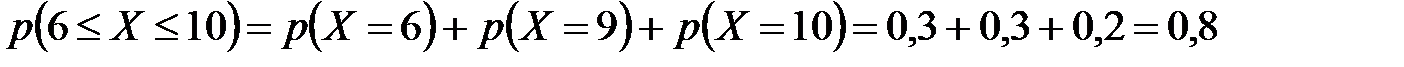 .
.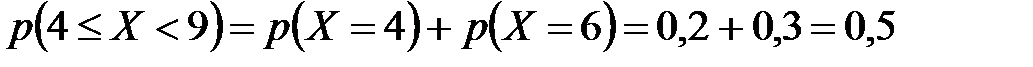 .
. .
.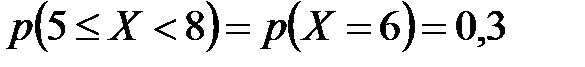 .
.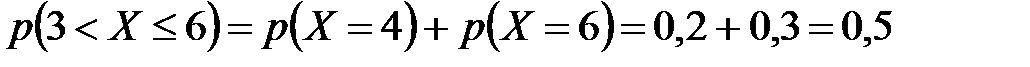 .
.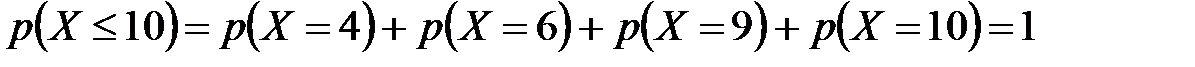 .
.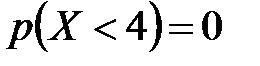 .
. .
. ;
; .
.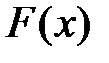 и построить ее график. Найти: а)
и построить ее график. Найти: а)  ; б)
; б) 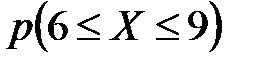 ; в)
; в)  ; г)
; г) 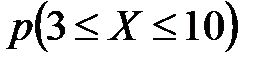 ; д)
; д)  ; е)
; е) 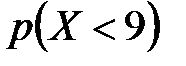 ; ж)
; ж)  ; з)
; з) 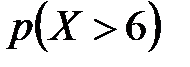 .
.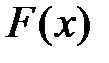 и построить ее график. Найти: а)
и построить ее график. Найти: а) 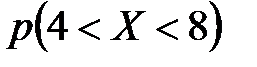 ; б)
; б)  ;
;


