

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Плотностью распределения вероятностей непрерывной случайной величины  называется функция
называется функция 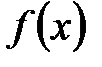 , которая является первой производной от функции распределения
, которая является первой производной от функции распределения 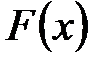 , то есть
, то есть
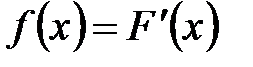 .
.
График плотности распределения вероятностей называется кривой распределения.
Иногда плотность распределения вероятностей 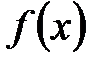 называют дифференциальной функцией распределения, а функцию распределения
называют дифференциальной функцией распределения, а функцию распределения 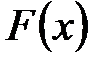 – интегральной функцией распределения.
– интегральной функцией распределения.
Свойства плотности распределения вероятностей:
1. Для любых  плотность распределения вероятностей
плотность распределения вероятностей 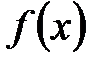 неотрицательна, то есть
неотрицательна, то есть  .
.
2. Для плотности распределения вероятностей имеет место равенство: 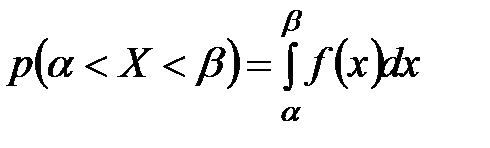 .
.
3. Для плотности распределения вероятностей имеет место равенство:  .
.
4. Для функции распределения и плотности распределения вероятностей имеет место равенство:  .
.
Свойство 2 геометрически означает, что площадь фигуры, ограниченной осью  , кривой распределения
, кривой распределения 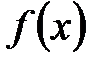 и прямыми
и прямыми 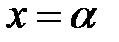 и
и 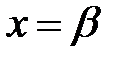 , равна вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу
, равна вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу 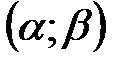 .
.
Свойство 3 означает, что площадь фигуры, ограниченной осью  и кривой распределения
и кривой распределения 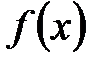 , равна единице.
, равна единице.
Свойство 4 позволяет найти функцию распределения 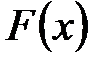 , зная плотность распределения
, зная плотность распределения 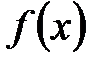 .
.
Пример 1. Непрерывная случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:

Найти вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  .
.
Воспользуемся для нахождения вероятности свойством 2 плотности распределения вероятностей.
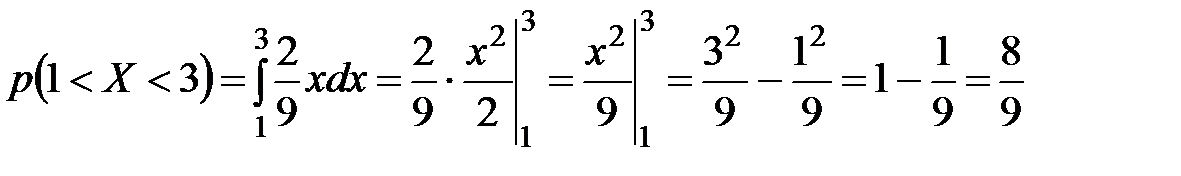 .
.
Пример 2. Непрерывная случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
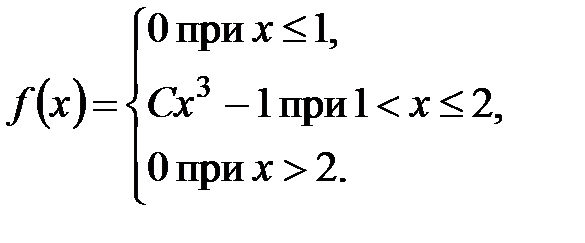
Найти постоянный параметр  .
.
Используя свойство 3 плотности распределения вероятностей, можем записать: 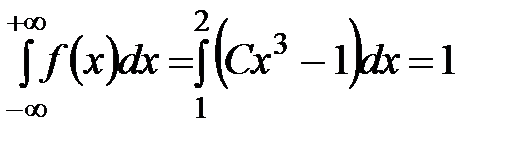 .
.
|
|
Вычислим определенный интеграл:
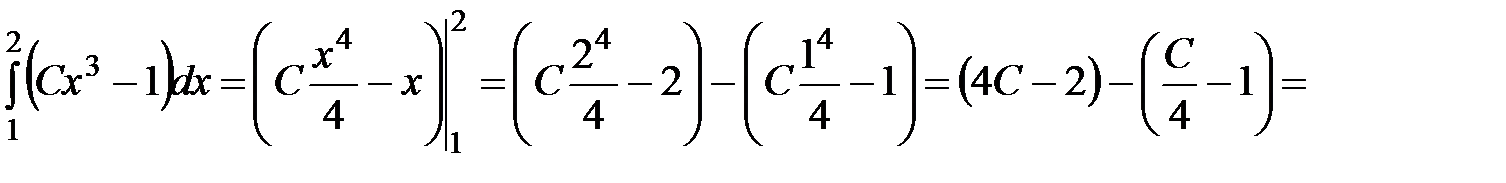
 .
.
Значит,  . Окончательно получаем
. Окончательно получаем 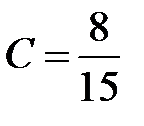 .
.
Задачи
1. Непрерывная случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
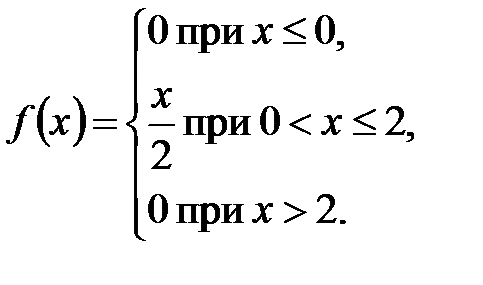
Найти вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 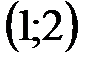 .
.
2. Задана плотность распределения вероятностей непрерывной случайной величины  :
:
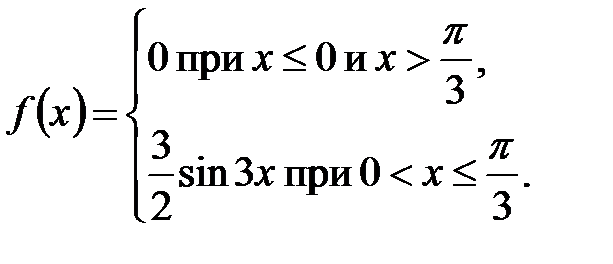
Найти вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 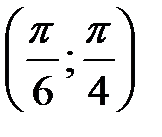 .
.
3. Непрерывная случайная величина  задана функцией распределения:
задана функцией распределения:
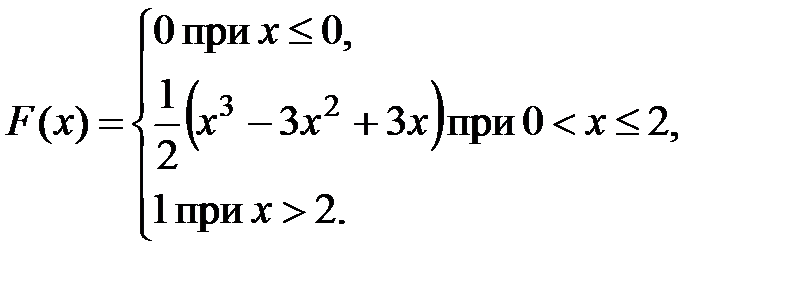
Найти вероятность того, что  примет значение, принадлежащее интервалу: а)
примет значение, принадлежащее интервалу: а) 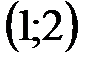 ; б)
; б)  ; в)
; в)  ; г)
; г) 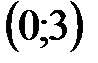 .
.
4. Является ли плотностью распределения вероятностей некоторой случайной величины каждая из следующих функций:
а) 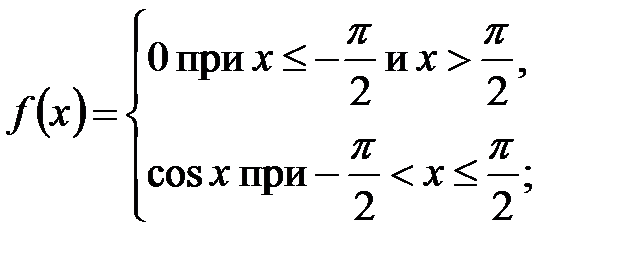
б) 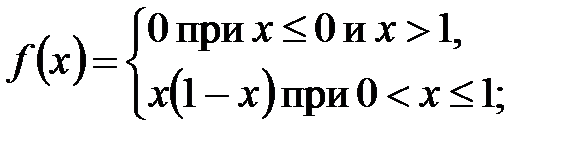
5. Задана плотность распределения вероятностей непрерывной случайной величины  :
:
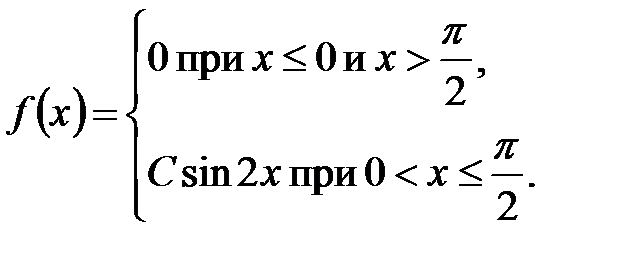
Найти постоянный параметр С.
6. Случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:

Найти постоянный параметр С.
Ответы
1. 0,75. 2. 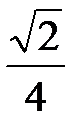 . 3. а) 0,5; б) 0,5; в)
. 3. а) 0,5; б) 0,5; в)  ; г) 1. 4. а) нет; б) нет. 5. 1. 6.
; г) 1. 4. а) нет; б) нет. 5. 1. 6. 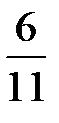 .
.
Числовые характеристики непрерывных случайных величин
Пусть непрерывная случайная величина 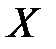 задана плотностью распределения вероятностей
задана плотностью распределения вероятностей 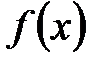 .
.
Математическое ожиданиенепрерывной случайной величины 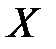 определяется равенством:
определяется равенством:
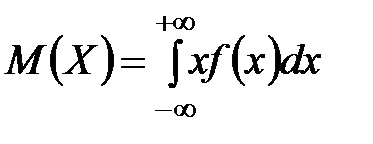 .
.
Дисперсия непрерывной случайной величины 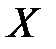 определяется равенством:
определяется равенством:
 .
.
Дисперсию удобно вычислять по формуле:
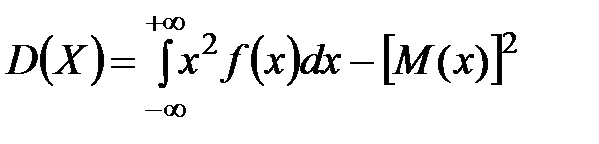 .
.
Предполагается, что все несобственные интегралы сходятся абсолютно.
Свойства математического ожидания и дисперсии, рассмотренные для дискретных случайных величин (п. 2.8), справедливы и для непрерывных случайных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для дискретной величины, равенством 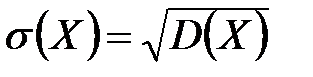 .
.
Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины  , заданной функцией распределения:
, заданной функцией распределения:
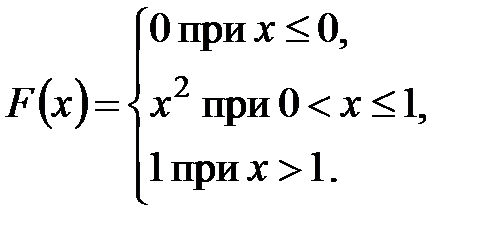
Найдем плотность распределения вероятностей величины 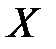 :
:
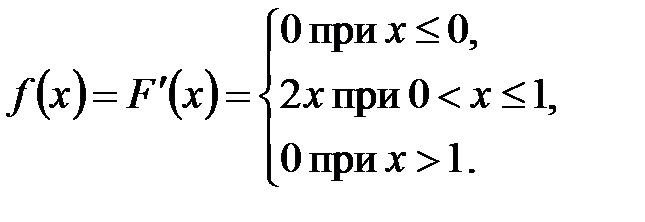
Найдем математическое ожидание:
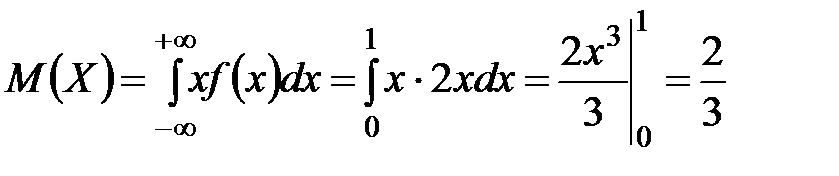 .
.
Найдем дисперсию и среднее квадратическое отклонение:
|
|
 ;
;
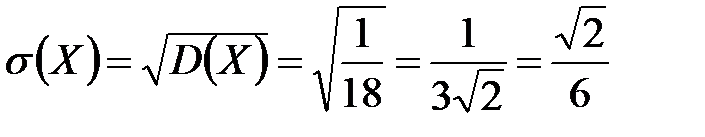 .
.
Задачи
1. Найти математическое ожидание и дисперсию случайной величины 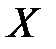 , заданной функцией распределения:
, заданной функцией распределения:
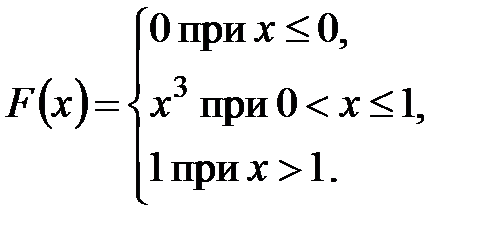
2. Найти математическое ожидание и среднее квадратическое отклонение случайной величины 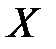 , заданной плотностью распределения вероятностей:
, заданной плотностью распределения вероятностей:
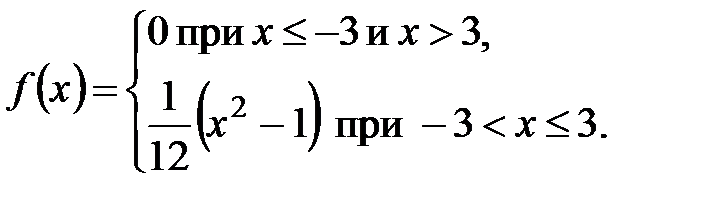
3. Задана плотность распределения вероятностей случайной величины  :
:
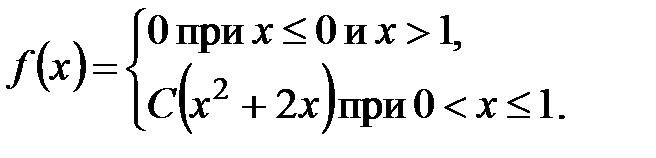
Найти: а) постоянный параметр С; б) математическое ожидание величины  .
.
4. Случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
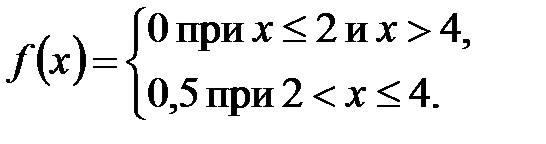
Найти: а) 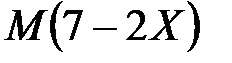 ; б)
; б) 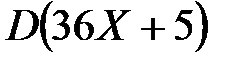 .
.
5. Случайная величина  задана функцией распределения:
задана функцией распределения:

Найти 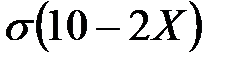 .
.
Ответы
1.  ,
, 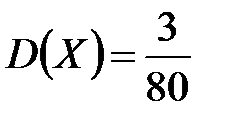 . 2.
. 2.  ,
,  . 3. а)
. 3. а) 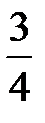 ; б)
; б)  . 4. а) 1; б) 12. 5.
. 4. а) 1; б) 12. 5. 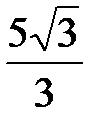 .
.
|
|
|

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!