Случайные величины                                                            18

А.А. Кудлаев

Учебное пособие

Технологии обработки информации средствами табличных процессоров. Теория вероятности

 

Москва

2018

Составитель: А. А. Кудлаев

Технологии обработки информации средствами электронных таблиц EXCEL Теория вероятностей. М. МИИГАиК, 2018.-42с.

Учебное пособие «Технологии обработки информации средствами электронных таблиц. Теория вероятностей» предназначено для студентов Высших учебных заведений, обучающихся по направлениям 120100 «Геодезия и дистанционное зондирование». Также может быть рекомендовано для студентов, обучающихся по направлениям 230400 «Информационные системы и технологии», 021300 «Картография и геоинформатика», 120700 «Землеустройство и кадастр», 230700 «Прикладная информатика».

Изложенный материал соответствует программе по информатике для технических и экономических специальностей ВУЗов. Теоретический материал сопровождается примерами, нацеленными на развитие у студентов навыков решения практических задач, а также вопросами и упражнениями для самостоятельного выполнения.

Рецензенты:

ОГЛАВЛЕНИЕ

Введение                                                                                               3

Основные понятия теории вероятностей                             4

Основные понятия комбинаторики                                      11

Случайные величины                                                            18

Законы распределения вероятностей                                   25

Литература                                                                                           42

Введение

Теория вероятностей – это математическая наука, изучающая закономерности случайных событий.

Случайные события – это события (явления), которые могут произойти, а могут и не произойти.

Примеры неслучайных событий:

· рождение – смерть,

· прилив – отлив,

· восход и закат солнца.

Не всегда можно предсказать наблюдаемые явления с помощью точных правил. Часто предположения делаются на основе статистических данных.

Например, нельзя точно предсказать погоду. Можно говорить о прогнозе лишь с некоторой долей уверенности. Занимаясь прогнозированием, человек оперирует событиями, которые могут иметь несколько различных исходов. Эти исходы и связанные с ними события имеют неодинаковые шансы на появление.

Количественное описание правдоподобия отдельных исходов и событий основывается на понятии вероятности. Каждому событию, возможному в данном случайном испытании, может быть приписана числовая мера его правдоподобия, называемая его вероятностью.

Анализом таких событий занимается теория вероятностей.

Основные понятия теории вероятностей

Понятие случайного события

Наблюдение какого-либо явления, происходящего при определенных условиях, в теории вероятностей принято называть испытанием (случайным испытанием).

Результат испытания является событием. Например, выполнение одиннадцатиметрового штрафного удара в футболе есть испытание, а попадание (или непопадание) в ворота – событие.

Все события делятся на элементарные и составные. Элементарные события содержат один исход, составные – несколько возможных исходов.

Говорят, что событие произошло, если свершился один из исходов, входящих в событие. Те исходы, при которых интересующее нас событие наступает, называются благоприятными исходами.

Особо выделяется невозможное событие, не содержащее ни одного исхода, то есть событие, которое никогда не сможет произойти.

Если появление одного из событий исключает появление других событий в этом же испытании, события называются несовместными.

Множество всех допускаемых исходов называется пространством элементарных событий.

Событие, состоящее в реализации какого-либо из всех элементарных событий пространства, – достоверное событие, которое произойдет обязательно, так как в нем содержится любой возможный исход.

События образуют полную группу, если в результате испытания появление хотя бы одного из них является достоверным. Например, при бросании игральной кости событие, состоящее в том, что в результате бросания кости выпадет 1, 2, 3, 4, 5 или 6 очков, является достоверным, а событие, состоящее в том, что в результате выпадет 7 или 8 очков, является невозможным.

Сумма событий

Произведение событий

Отрицание

Событие А является отрицанием или называется противоположным событию А, если оно содержит все исходы пространства событий, не вошедшие в А. Возвращаясь к рассматриваемому примеру, получим, что отрицание события А состоит в том, что в результате бросания кости выпадет 4, 5 или 6 очков.

Разность

Разностью С = А - В называется событие С, содержащее все исходы А, не входящие в B. В условиях предыдущего примера разностью А - В является событие, состоящее в том, что в результате бросания кости выпадет 1 или 2 очка.

Вероятность события

Каждому элементарному событию A пространства ставится в соответствие числовая мера его правдоподобия, называемая вероятностью этого события Р(А). Вероятностью события А называется отношение числа благоприятных элементарных исходов к числу всех возможных исключающих друг друга исходов. Здесь A – событие, n – число всех возможных исходов, m – число благоприятных исходов, P(A) – вероятность события А.

События, вероятности которых одинаковы, называются равновероятными. Для равновероятных событий вероятности вычисляются по формуле Р(A) = 1/k, где k – число элементарных событий пространства.

Например, бросание игральной кости приводит к выпадению одной из шести граней. Это шесть элементарных исходов, которые являются равновероятными. Следовательно, вероятность каждого из них равна 1/6.

Свойства вероятности

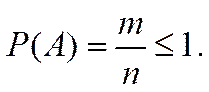
1. Вероятность любого случайного события неотрицательна и не больше 1. Пусть А – случайное событие и m £ n. Следовательно, 0 £ Р(A)£ 1 для любого события A.

2. 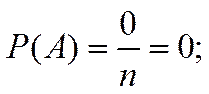Вероятность достоверного события равна единице. Если А – достоверное событие, то m = n

3. Вероятность невозможного события равна нулю. Если А – невозможное событие, то m = 0

 

4. Вероятностью Р(A + В) составного события А + В называется сумма вероятностей элементарных событий (исходов), составляющих A и В:

P(A+B)=P(A)+P(B)

5. Если события A и В несовместны, то в общем случае:

P(A+B)=P(A)+P(B)-P(AB)

Пример. Какова вероятность того, что наугад вырванный из календаря листок соответствует 30 числу, если в году 365 дней?

Решение. Событие А – на листке календаря число 30. Количество всех возможных исходов n = 365. Количество благоприятных исходов m = 11.

Получаем, что вероятность события А:

Ответ: вероятность того, что вырванный наугад из календаря листок соответствует 30 числу, равна

P (А) = 0,03.

Условная вероятность

Если на событие А влияет исход некоторого события В (произошло ли событие В и с каким именно исходом, наступает или не наступает определенный исход А), речь идет об условной вероятности А при условии В.

Например, если известны доли учеников школы, знающих французский и немецкий языки, а также доля учеников, знающих оба эти языка. То доля учеников, знающих французский язык среди учеников, знающих немецкий язык, на языке теории вероятностей называется условной вероятностью события «знать французский» при условии события «знать немецкий»

Условной вероятностью события А при условии события В называется отношение вероятностей:

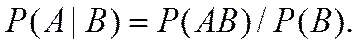
Количество информации

Информацию можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности знаний, то говорят, что такое сообщение содержит информацию. Количество информации для событий с различными вероятностями определяется по формуле:

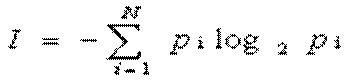
где I – количество информации, N – количество возможных событий,
p_i- вероятности отдельных событий.

Если события равновероятны, то количество информации определяется по формуле: I = log₂N или из показательного уравнения: N = 2^I.

Упражнения:

1. Бросают два кубика: красный и синий. Считая все комбинации цифр на красном и синем кубиках равновозможными, определите вероятность того, что цифры на красном и синем кубиках будут одинаковы.

2. Бросают два кубика: красный и синий. Считая все комбинации цифр на красном и синем кубиках равновозможными, определите, какая из сумм будет наиболее вероятной.

3. Бросают два кубика: красный и синий. Считая все комбинации цифр на красном и синем кубиках равновозможными, определите, какая из сумм будет иметь наибольшую вероятность: 3 или 10?

4. Опыт состоит в одновременном бросании четырех кубиков (красного, синего, зеленого, желтого). Найдите вероятность того, что

а) выпадут четыре шестерки;

б) выпадут три шестерки и одна пятерка;

в) выпадут две шестерки и две пятерки;

г) выпадет ровно одна шестерка;

д) выпадут четыре разные цифры;

е) не выпадет ни одной шестерки;

ж) выпадет хотя бы одна шестерка.

5. В очередь в случайном порядке становятся четыре человека А, Б, В, Г. Считая все варианты расположения их равновозможными, определите вероятность следующих событий:

а) А будет первым в очереди;

б) Б не будет последним в очереди;

в) А будет стоять раньше Б;

г) А будет стоять рядом с Б (до или после него);

д) А будет стоять раньше Б и раньше В;

е) А будет стоять раньше Б, а В будет стоять раньше Г.

6. Среди учеников школы 15% знают французский язык и 20% знают немецкий язык. Доля учеников, знающих оба эти языка, составляет 5%. Какова доля учеников, знающих французский язык, среди учеников, знающих немецкий язык?

Основные понятия комбинаторики

Перестановки

Перестановкой n элементов множества называется их комбинация, отличающаяся порядком расположения.

В комбинаторике принято обозначение: если в множестве имеется n элементов, то П_n — число перестановок элементов этого множества.

Рассмотрим конкретные множества:

n = 0: П₀ = 1 - по определению;

n = 1: П₁ = 1;

n = 2: есть множество {1,2}, возможны числа 12 и 21, значит, П₂ = 2;

n = 3: сколько различных трехзначных чисел можно составить из множества {1, 2, 3}?

Начнем с тех, которые начинаются с 1: 123, 132, затем с 2: 213, 231 и
с 3: 312 и 321. Всего получается 6 чисел. Это значит, что П₃ = 6.

Можно предположить, что П_n = n ´ П_n-1

Вычислить

1	2	3

 

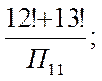
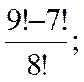
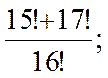
Сочетания

Пример: какие наборы можно составить из различного количества предметов, если всего их 4 — шампанское, печенье, конфеты, апельсины?

Были составлены наборы из 1 предмета, из 2, из 3, из 4, на основе исходных 4 предметов. Иначе можно сказать: были составлены подмножества из 1, 2, 3, 4 предметов, из 4 элементов данного множества. Такие подмножества называются сочетаниями.

По одному предмету	По два предмета	По три предмета	По четыре предмета
Ш	Ш, А	Ш, А, П	Ш, А, П, К
А	Ш, К	Ш, А, К
П	Ш, П	П, К, А
К	К, П	П, К, Ш
	К, А
	П, А
Всего 4	Всего 6	Всего 4	Всего 1

Сочетаниями называются конечные подмножества, составленные из элементов данного множества. Если в множестве элементов - n, а в подмножестве m, то общее количество всех сочетаний обозначается и читается как число сочетаний из n элементов по m, при этом n >.

Формула для вычисления числа сочетаний:

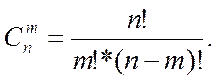
Для нахождения числа сочетаний в Excel используется функция — ЧИСЛКОМБ. В функции ЧИСЛКОМБ (число; число_выбранных) должны быть заданы следующие параметры: число -число объектов n; число_выбранных - число объектов в каждой комбинации m.

Упражнения:

Размещения

Из Санкт-Петербурга в Москву можно добираться самолетом, поездом, на автомобиле. Из Москвы во Владивосток можно долететь, доплыть, доехать поездом. Сколькими способами можно добраться из Санкт-Петербурга до Владивостока через Москву?

Случайные величины

Переменная величина, принимающая различные числовые значения, называется случайной величиной. Допустим, что некоторая величина X может принимать значения: x ₁, x ₂,…, x_{k .} Каждый раз, как выполняется некоторое сочетание условий, величина X принимает одно из этих значений. Вероятности для X принять то или иное значение равны p ₁, p ₂,…, p_{k .} Очевидно, должно выполняться равенство:

поскольку x ₁, x ₂,…, x_{k .} - полная группа событий.

Если вероятности p ₁, p ₂,…, p_k известны, то говорят, что распределение случайной величины X известно и случайная величина X задана.

Числовые характеристики распределения вероятностей помогают составить наглядное представление об этом распределении. Наиболее часто употребляемыми характеристиками случайной величины служат моменты и квантили.

Первый момент случайной величины X, называемый также математическим ожиданием, или средним значением обозначается М X.

Математическим ожиданием дискретной случайной величины со значениями x ₁, x ₂,..., имеющими вероятности p ₁, p ₂,..., является

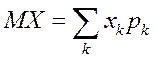
Биномиальное распределение

Биномиальное распределение - одно из самых распространенных дискретных распределений. Оно возникает в тех случаях, когда ищут, сколько раз происходило некоторое событие в серии из известного числа независимых наблюдений, выполняемых в одинаковых условиях. При этом распределении разброс вариант является следствием влияния ряда независимых и случайно сочетающихся факторов.

Примером дискретной случайной величины, подчиняющейся биномиальному закону распределения, является число появлений события А при выполнении n испытаний. Возможными значениями этой случайной величины m являются 0,1,2,..., п.

Если для каждого отдельного испытания ввести случайную величину x, которая может принимать только два значения: 1 с вероятностью р и 0 с вероятностью q = (1 - р),то соответствующие вероятности появления т успешных случайных величин x вычисляются по формуле:

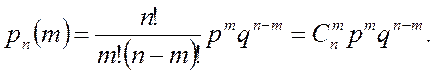
Эта формула называется формулой Бернулли, которая определяет распределение случайной величины - числа появлений события А при n испытаниях, называемое биномиальным распределением.

Если число испытаний n велико, а вероятность р реализации события А в одном испытании не близка ни к 0 и ни к 1, то маловероятно, чтобы событие А при n испытаниях случилось очень малое число раз или число раз, близкое к п.

Очевидно, что при т, равном малому числу, вероятность p_n(m) растет с увеличением т, а для т, близких к n, она убывает при увеличении т.

Математическое ожидание и дисперсия случайной величины, имеющей биномиальное распределение, равны:

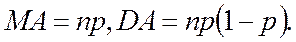
Примером практического использования биномиального распределения является контроль качества партии изделий, когда сплошная проверка качества не возможна (изделие, прошедшее испытание, не подлежит дальнейшему использованию).

Для контроля из партии наудачу выбирают определенное количество образцов изделий (n). Эти образцы проверяют и регистрируют число бракованных изделий (m). Теоретически число бракованных изделий может быть любым, от 0 до n, но вероятности этих чисел различны.

В основе принятия решения лежит сравнение распределения результатов контроля, полученных опытным путем, и теоретического распределения, при котором гарантируется необходимое качество всей партии - низкая вероятность брака P(m £ k), где k - предельное число бракованных изделий.

В Excel для вычисления вероятности отдельного значения биномиального распределения или значения случайной величины по заданной вероятности используются функции БИНОМРАСП и КРИТБИНОМ.

Функция БИНОМРАСП применяется для вычисления вероятности в задачах с фиксированным числом испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, и вероятность успеха постоянна на протяжении всего эксперимента.

Функция КРИТБИНОМ вычисляет наименьшее значение числа успешных исходов случайной величины, для которого интегральное биномиальное распределение больше или равно заданной величине (критерию). Эта функция наиболее часто используется в приложениях, связанных с контролем качества.

Пример 1. Какова вероятность того, что трое из четырех следующих новорожденных будут мальчиками?

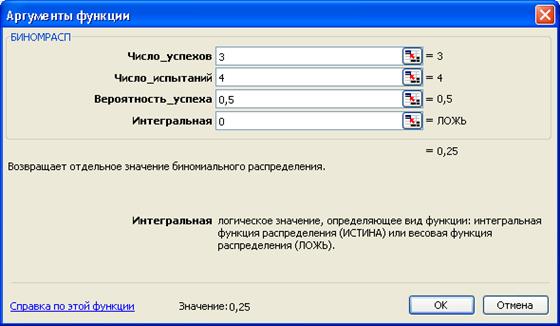
Таким образом, ровно трое мальчиков из четырех новорожденных могут появиться с вероятностью p = 0,25.

Пример 2. Какова вероятность того, что появится не более трех мальчиков из четырех следующих новорожденных?

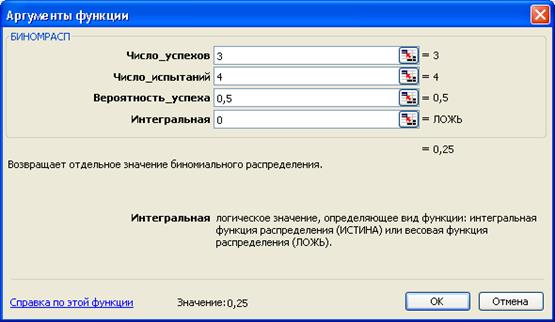
Вероятность этого события будет равна p = 0,9375.

Пример 3. Построить диаграмму биномиальной функции плотности вероятности Р (А= m)при n = 10 и p = 0,2.

В ячейку А1 вводим «m» - количества успешных исходов, в ячейку В1
«p» - вероятность. Заполняем диапазон А2:А12 возможными значениями исходов: 0, 1, 2,…,10.

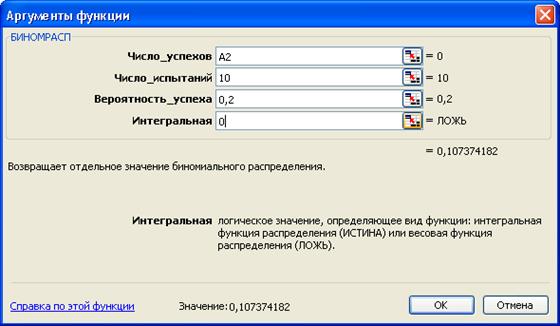
Из ячейки В2 копируем функцию БИНОМРАСП в диапазон ВЗ:В12. По полученным данным строим искомую диаграмму биномиальной функции распределения.

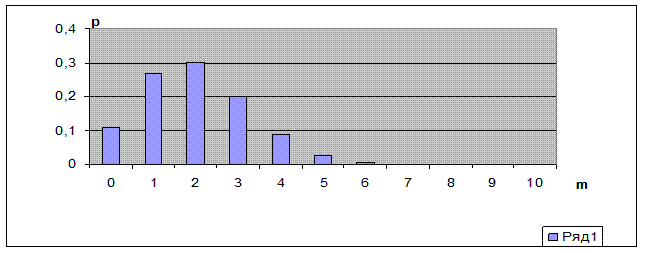
Пример 4. Для биномиальной функции плотности вероятности из примера 3. найти значение числа m, для которого вероятность интегральногораспределения P ≥ 0,3.

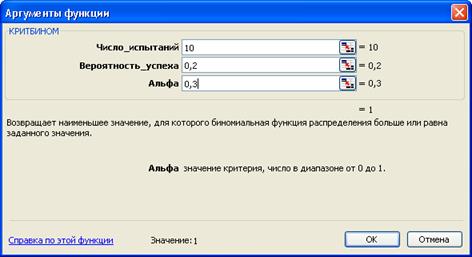
Число успешных событий m = 1.

Упражнения:

29. При бросании монеты может выпасть орел или решка. Вероятность того, что при очередном бросании выпадет орел, равна 0,5. Найти вероятность того, что орел выпадет в точности 6 раз из 10.

30. Построить диаграмму биномиальной функции плотности вероятности Р(А=т) при n = 10 и р = 0,5.

31. Построить диаграмму биномиальной интегральной функции распределения Р (A £ m)при n = 10 и p = 0,2.

При выборочном контроле продукции из партии в 100 изделий выбирается 20 и при обнаружении в этой выборке хотя бы одного дефектного изделия вся партия бракуется. В партии имеется 10 дефектных изделий. Какова вероятность того, что хотя бы одно дефектное изделие попадет в выборку?

Большинство экспериментальных исследований связаны с измерениями, результаты которых могут принимать любые значения в заданном интервале, и описываются моделью непрерывных случайных величин. Одним из важнейших непрерывных распределений является нормальное, или гауссово распределение.

Нормальное распределение получило широкое распространение для приближенного описания многих случайных явлений, в которых на результат воздействует большое количество независимых случайных факторов. Многие распределения, связанные со случайной выборкой, при увеличении ее объема переходят в нормальные.

Плотность вероятностей нормально распределенной случайной величины задается формулой:

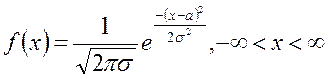
Здесь а и s - параметры распределения. Иногда используют краткое обозначение N (a, s ²).

График плотности (нормальная кривая):

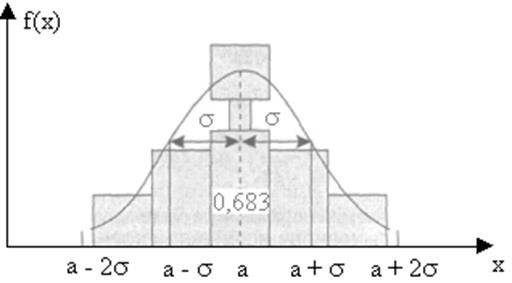
Воспользуемся функцией НОРМСТРАСП для вычисления стандартного нормального интегрального распределения. Это распределение имеет среднее равное нулю и стандартное отклонение равное единице. Эта функция может использоваться вместо таблицы для стандартной нормальной кривой.

Функция имеет параметры:

вероятность - вероятность, соответствующая нормальному распределению;

среднее - среднее арифметическое распределения;

стандартное_отклонение - стандартное отклонение распределения.

НОРМОБР (0,75;24,3;1,5) = 25,31174 – верхняя квартиль

НОРМОБР (0,25;24,3;1,5) = 23,28826 – нижняя квартиль

Упражнения:

34. Найти вероятность того, что появится случайная величина х £42 при нормальном законе распределения вероятностей с М = 40 и s = 1,5.

35. Построить диаграмму нормальной функции плотности вероятности f(x) при М = 10 и s = 2.

36. Построить диаграмму интегральной нормальной функции распределения вероятности f(x) при М = 30 и s = 3.

37. Найти квантиль для p = 0,908789 и нормального распределения с
М = 40 и s = 1,5.

38. Найти нормализованное значение х, если x = 21, М = 20, s = 1,5.

Другие законы распределения

На практике помимо биномиального и нормального распределений приходится сталкиваться со случайными величинами, распределенными по:

· равномерному закону,

· закону Пуассона,

· закону с показательным распределением,

· законам, связанным с нормальным: Хи-квадрат, Стьюдента и Фишера.

Равномерное распределение

Распределение Пуассона

Показательное распределение

Распределение хи-квадрат

Это непрерывное распределение, связанное с нормальным распределением. Если случайные величины x ₁, x ₂, …, x_n независимы, и каждая из них имеет стандартное нормальное распределение N (0,1), то случайная величина 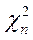, определенная как:

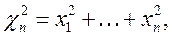
имеет распределение хи-квадрат с n степенями свободы. Математическое ожидание и дисперсия случайной величины равны:

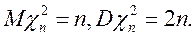
В Excel для вычисления значений распределения хи-квадрат используются функции:

ХИ2РАСП (х; степени_свободы)
ХИ20БР (вероятность; степени _ свободы)

Распределение Стьюдента

Непрерывное распределение, связанное с нормальным. Если случайные величины x₁, x₂, …, x_n - независимы, и каждая из них имеет стандартное нормальное распределение N (0,1), то случайная величина:

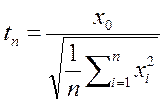
имеет распределение, называемое распределением Стьюдента. Математическое ожидание и дисперсия случайной величины равны:

В Excel для вычисления значений распределения Стьюдента используются функции:

СТЬЮДРАСП (x;степени свободы;хвосты)

СТЬЮДРАСПОБР (вероятность;степени_свободы),

которые при заданном числе степеней свободы вычисляют вероятность (по заданному численному значению х, для которого требуется вычислить распределение) и t - значение распределения Стьюдента (по заданной вероятности), соответственно.

F-распределение (Фишера)

Непрерывное распределение, связанное с нормальным. Если случайные величины x ₁, x ₂, …, x _m и y ₁, y ₂, …, y _n (n и m - натуральные числа) - независимы, и каждая из них имеет стандартное нормальное распределение N(0,1), то случайная величина F_m,n:

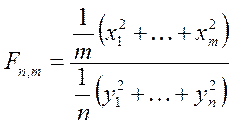
имеет F-распределение с параметрами m и n, называемыми степенями свободы.

Математическое ожидание и дисперсия случайной величины F_m,n равны:

для n > 2,

для n > 4.

В Excel для вычисления значений F-распределения используются функции F РАСП и FРАСПОБР (х;степени_свободы1;степени_свободы2), которые при заданном числе степеней свободы m и n вычисляют вероятность (по заданному численному значению F_{m , n}, для которого требуется вычислить распределение) и численное значение F_{m , n} (по заданной вероятности), соответственно.

ЛИТЕРАТУРА

1. Гаврилова В.В., Кудлаев А.А., Семов А.М. Информационные технологии. Офисные приложения. Учебное пособие. М.: МИИГАиК, 2012. – 60 с.

2. Гельман В.Я. Решение математических задач средствами EXCEL: Практикум. СПб.: Питер, 2003. – 240 с.

3. Ниворожкина Л.И., Морозова З.А. Теория вероятностей и математическая статистика. – М.: Эксмо, 2008. – 432 с. (Техническое образование).

4. Шень А. Вероятность: примеры и задачи. – М.: МЦНМО, 2012. – 72 с.

 

А.А. Кудлаев

Учебное пособие

Технологии обработки информации средствами табличных процессоров. Теория вероятности

 

Москва

2018

Составитель: А. А. Кудлаев

Технологии обработки информации средствами электронных таблиц EXCEL Теория вероятностей. М. МИИГАиК, 2018.-42с.

Учебное пособие «Технологии обработки информации средствами электронных таблиц. Теория вероятностей» предназначено для студентов Высших учебных заведений, обучающихся по направлениям 120100 «Геодезия и дистанционное зондирование». Также может быть рекомендовано для студентов, обучающихся по направлениям 230400 «Информационные системы и технологии», 021300 «Картография и геоинформатика», 120700 «Землеустройство и кадастр», 230700 «Прикладная информатика».

Изложенный материал соответствует программе по информатике для технических и экономических специальностей ВУЗов. Теоретический материал сопровождается примерами, нацеленными на развитие у студентов навыков решения практических задач, а также вопросами и упражнениями для самостоятельного выполнения.

Рецензенты:

ОГЛАВЛЕНИЕ

Введение                                                                                               3

Основные понятия теории вероятностей                             4

Основные понятия комбинаторики                                      11

Случайные величины                                                            18