Системы линейных уравнений
Обратимся к изучений системы линейных дифференциальных уравнений
 (3.1.1)
(3.1.1)
Система (3.1.1) называется однородной, если ¦ i (x) = 0 (i = 1, …, n) в противном случае - неоднородной. Будем предполагать aik(x) и ¦i(x) непрерывными на интервале X. Как было доказано выше, при этих условиях на Х существует единственное решение системы (3.1.1), удовлетворяющее начальному условию
i(x0) = 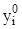 , i = 1, …, n. (3.1.2)
, i = 1, …, n. (3.1.2)
Для системы уравнений справедливы теоремы, аналогичные тем, которые были доказаны для одного уравнения n-го порядка.
Общие свойства системы линейных уравнений. Обратимся системе (3.1.1). Обозначим через у, ¦ и y0 столбцы

а через А (х) обозначим (n ´ n) - матрицу с элементами аij(х):

Тогда систему (3.1.1) можно записать в виде одного уравнения
' = A (x) y + f {x), (3.1.3)
точно так же, как и начальные условия
(x0) = y0. (3.1.4)
Пользуясь правилом умножения 4°, правилом сложения3° иправилом равенства матриц 2°, нетрудно убедиться в том, что (3.1.3) и (3.1.4) то же самое, что и (3.1.1) и (3.1.2).
В силу свойств умножения и дифференцирования матриц для дифференцируемых столбцов имеет место тождество, в котором ai - постоянные числа,
 (3.1.5)
(3.1.5)
выражающее свойство линейности оператора y¢ - Ay º L[y] на множестве дифференцируемых столбцов.
Здесь и в дальнейшем для нумерации столбцов будем употреблять индекс, заключенный в круглые скобки, оставляя индекс без скобок для обозначения элементов (компонент).
Непосредственным следствием этого тождества является принцип суперпозиции.
Теорема 3.1.1. Пусть в уравнении (3.1.3) f (x) является линейной комбинацией f (i)(х),т.е.

где ai - постоянные числа, и пусть y(i)(x)является решением уравненияy'(i) = A(x) y(i) + f (i).
Тогда линейная комбинация y(i) (x) с теми же коэффициентамиai, т.е. столбец у (х) =  ,является решением уравнения (3.1.3).
,является решением уравнения (3.1.3).
Имеют также место теоремы, аналогичные теоремам 1.4-1.6.
Однородное уравнение. Рассмотрим более детально однородное уравнение
у ' = А (х) у. (3.1.6)
Пусть имеется п столбцов

Составим из этих столбцов матрицу W(x):
 (3.1.7)
(3.1.7)
Сопоставим уравнению (3.1.6), правая и левая части которого - столбцы, аналогичное уравнение
¢ = A (x) W, (3.1.8)
правая и левая части которого - матрицы размерности (n ´ n)и в котором неизвестной является матрица W(x).
Теорема 3.1.2. Пусть y(1),..., у(n) есть n решений уравнения (3.1.6). Тогда (n ´ n) - матрица W(x), образованная из них по формуле (3.1.7), является решением матричного уравнения (3.1.8).
Обратно: если W(x) является решением уравнения (3.1.8), то каждый столбец матрицы W(x) является решением уравнения (3.1.6).
Доказательство. Достаточно расписать (3.1.8) и (3.1.6) поэлементно. Действительно, (3.1.8) означает
 (3.1.9)
(3.1.9)
или
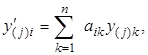 (3.1.10)
(3.1.10)
a (3.1.6) означает
 (3.1.11)
(3.1.11)
Поэтому если у(j) являются решениями (3.1.6), то каждое у(j) удовлетворяет (3.1.11), т.е. справедливо (3.1.10) или, что то же, (3.1.9), а значит, и (3.1.8), и наоборот, если справедливо (3.1.8), то и (3.1.10), а это в сопоставлении с (3.1.11) означает, что у(j) (j = 1,..., n) является решением уравнения (3.1.6).
Отметим еще следующие факты, проверяемые столь же просто.
Теорема 3.1.3. Если W(x) - решение уравнения (3.1.8), то выражение WB является решением уравнения (3.1.6), если В - произвольный постоянный столбец, и решением уравнения (3.1.8), если В - произвольная постоянная (n ´ n) - матрица.
Определение. Будем говорить, что столбцы u(i),..., u(р) линейно зависимы на интервале X, если существуют постоянные C1,..., Ср, не все равные нулю, такие, что имеет место тождество
 (3.1.12)
(3.1.12)
Если же (3.1.12) выполняется только при C1 =... = Ср = 0, то будем говорить, что u(1), …, u(p) линейно независимы.
Рассмотрим n дифференцируемых столбцов у(1),..., у(n). Запишем для них равенство (3.1.12):
 (3.1.13)
(3.1.13)
Введем в рассмотрение постоянный столбец 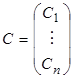 . Пользуясь этим столбцом и матрицей W(x}, составленной из у(i) по правилу (3.1.7), можно (3.1.13) записать в виде
. Пользуясь этим столбцом и матрицей W(x}, составленной из у(i) по правилу (3.1.7), можно (3.1.13) записать в виде
= 0. (3.1.14)
Так как, согласно правилу матричного исчисления, 2° считается С = 0, если все Сi (i = 1,..., n) равны нулю, то определение линейной зависимости и независимости у(i), …, y(n) можно сформулировать следующим образом.
Определение. Будем говорить, что столбцы y(1),..., y(n) линейно зависимы на интервале X, если существует постоянный столбец C ¹ 0 такой, что тождественно на Х имеет место (3.1.14).
В противном случае, т.е. если (3.1.14) справедливо только при С = 0, будем говорить, что y(1),..., y(n) линейно независимы.
Определение. Назовем ∆(x) = Det W(x) определителем Вронского для y(1),..., y(n).
Теперь можно сформулировать и доказать теоремы, аналогичные теоремам 1.7 - 1.9 из теории уравнения n-го порядка. Все эти доказательства записываются весьма компактно, если пользоваться введенной матричной записью, которая очень удобна и требует лишь некоторого навыка.
Теорема 3.1.4. Если решения y(1),..., y(n) уравнения (3.1.6) линейно зависимы на X, то ∆(x) º 0 на X.
Доказательство.
Имеем WC = 0, С ¹ 0. Эта запись является кратким обозначением того факта, что при каждом х величины C1,..., Сn удовлетворяют системе линейных алгебраических уравнений с определителем ∆ (x), и так как решение нетривиальное, то ∆ (x) = 0 при любом х Î X, т.е. ∆(x} º 0.
Теорема 3.1.5. Если ∆ (x) = 0 хотя бы для одного х0 Î X, то, решения y(1),..., y(n) уравнения (3.1.6) линейно зависимы на Г.
Доказательство.
Запишем кратко доказательство этой теоремы, уже не давая дополнительных разъяснений, как в предыдущей. Возьмем x0 Î X, и пусть, ∆ (x0) = 0. Составим уравнение W(x0) C = 0 относительно С. В силу ∆ (x0) = 0 существует решение С ¹ О. Положим у (x) = W (x) С. Согласно теореме 3.1.3 это решение уравнения (3.1.6), причем y (x0) = W (x0) C = 0, а тогда, в силу теоремы единственности, y (x) º 0 и, таким образом, W (х) С º 0, что, означает линейную зависимость y(1),..., y(n).
Теорема 3.1.6. (альтернатива). Определитель Вронского либо тождественно равен нулю, и это означает, что решения y(1),..., y(n) линейно зависимы, либо не обращается в нуль ни в одной точке X, и это означает, что решения y(1),..., y(n) линейно независимы.
Определение. Фундаментальной системой решений уравнения (3.1.6) будем называть n линейно независимых решений y(1),..., y(n) уравнения (3.1.6), а соответствующую им по формуле (3.1.7) матрицу W{x) будем называть фундаментальной матрицей.
На основании теоремы 3.1.5. можно дать другое (эквивалентное) определение фундаментальной матрицы.
Определение. Решение W(x) уравнения (3.1.8), для которого ∆(х} отлично от нуля всюду на X, называется фундаментальной матрицей.
Теорема 3.1.7. Линейная однородная система уравнений имеет фундаментальную матрицу.
В силу теоремы 3.1.6. достаточно взять произвольную матрицу а = const с отличным от пуля определителем и задать для W начальное условие W (x0) = a.
Теорема 3.1.8. Если W (x) - фундаментальная матрица, то любое решение у(х) уравнения (3.1.6) представимо в виде
(x) = W (x) C, (3.1.15)
где С - некоторый постоянный столбец.
Доказательство.
Пусть y (x0) = y0. Определим С уравнением W (x0) C = у0, которое разрешимо в силу ∆ (x0) ¹ 0. Построим  (х) = W (x) C. Так как
(х) = W (x) C. Так как  (xо) = W(x0) C = y0, то в силу теоремы единственности у (х) º
(xо) = W(x0) C = y0, то в силу теоремы единственности у (х) º 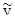 (х) = W (x) C, что и требовалось.
(х) = W (x) C, что и требовалось.
Замечание. На языке линейной алгебры теоремы 3.1.7. и 3.1.8. означают, что, пространство решений уравнения (3.1.6) n-мерно.
Построим решение уравнения (3.1.6), удовлетворяющее условиям (3.1.4), выразив с помощью W (x) величину С через у0. Имеем
(x0) = W (x0) C = y0,
откуда
С = W- 1 (x0) у0
и, следовательно,
y (x) = W (x) W- 1 (x0) y0.
Матрицу Â (х, х0) = W (х) W- 1 (х0), являющуюся функцией двух переменных х и x0, назовем импульсной матрицей, или матрицантом. В силу теоремы 3.1.3. Â (х, х0) как функция х удовлетворяет уравнению (3.1.8). Кроме того, очевидно, что
 (х, х0) = E.
Таким образом, справедлива
Теорема 3.1.9. Решение задачи (3.1.6), (3.1.4) имеет вид
(x) = Â (x, x0) y0, (3.1.16)
где матрица Â (х, x0) удовлетворяет по аргументу х матричному уравнению (3.1.8) и условию Â (х, x0) = Е.
Неоднородное уравнение. Рассмотрим теперь неоднородное уравнение (3.1.3).
Теорема 3.1.10. Если W (х) - фундаментальная матрица, а  (х) - частное решение неоднородного уравнения (3.1.3), то любое решение у (х) уравнения (3.1.3) представило в виде
(х) - частное решение неоднородного уравнения (3.1.3), то любое решение у (х) уравнения (3.1.3) представило в виде
(x) = W (x) C +  (x), (3.1.17)
(x), (3.1.17)
где С - некоторый постоянный столбец.
Доказательство точно такое же, как в случае уравнения n-го порядка, и мы его опускаем.
Построим частное решение  (х), удовлетворяющее нулевым начальным условиям
(х), удовлетворяющее нулевым начальным условиям  (x0) = 0. Будем искать его в виде
(x0) = 0. Будем искать его в виде
 (x) = W (x) C (x),
(x) = W (x) C (x),
где С (x)-неизвестный столбец. Это фактически просто замена переменных. Подставляя  (х) в (3.1.3), получим
(х) в (3.1.3), получим
W' C + W C' = AWC + f.
Так как W удовлетворяет (3.1.8), то W¢ - AW = 0 и, следовательно, WC' = f. Отсюда C' = W- 1 f. А так как 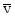 (x0) = W(x0) C(x0) = 0, то С (х0) = 0 и, следовательно,
(x0) = W(x0) C(x0) = 0, то С (х0) = 0 и, следовательно,

Таким образом,

и справедлива
Теорема 3.1.11. Частное решение 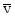 (х)'уравнения (3.1.3), удовлетворяющее условию
(х)'уравнения (3.1.3), удовлетворяющее условию 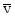 (х0) = 0, имеет вид
(х0) = 0, имеет вид
 (3.1.18)
(3.1.18)
где Â (х, x) - импульсная матрица, или матрицант, - решение матричного уравнения (3.1.8), удовлетворяющее условию Â (x, x) = E.
Замечания. 1. Изложенный метод построения частного решения системы линейных уравнений фактически является вариантом метода вариации постоянных, который для одного уравнения использовался в гл. 1. п. 1.1.
2. В силу принципа суперпозиции решение у (х) задачи (3.1.3), (3.1.4) имеет вид
 (3.1.19)
(3.1.19)



 (3.1.1)
(3.1.1)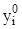 , i = 1, …, n. (3.1.2)
, i = 1, …, n. (3.1.2)

 (3.1.5)
(3.1.5)
 ,является решением уравнения (3.1.3).
,является решением уравнения (3.1.3).
 (3.1.7)
(3.1.7) (3.1.9)
(3.1.9)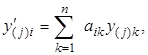 (3.1.10)
(3.1.10) (3.1.11)
(3.1.11) (3.1.12)
(3.1.12) (3.1.13)
(3.1.13)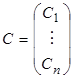 . Пользуясь этим столбцом и матрицей W(x}, составленной из у(i) по правилу (3.1.7), можно (3.1.13) записать в виде
. Пользуясь этим столбцом и матрицей W(x}, составленной из у(i) по правилу (3.1.7), можно (3.1.13) записать в виде (х) = W (x) C. Так как
(х) = W (x) C. Так как 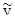 (х) = W (x) C, что и требовалось.
(х) = W (x) C, что и требовалось. (х) - частное решение неоднородного уравнения (3.1.3), то любое решение у (х) уравнения (3.1.3) представило в виде
(х) - частное решение неоднородного уравнения (3.1.3), то любое решение у (х) уравнения (3.1.3) представило в виде (х), удовлетворяющее нулевым начальным условиям
(х), удовлетворяющее нулевым начальным условиям 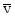 (x0) = W(x0) C(x0) = 0, то С (х0) = 0 и, следовательно,
(x0) = W(x0) C(x0) = 0, то С (х0) = 0 и, следовательно,

 (3.1.18)
(3.1.18) (3.1.19)
(3.1.19)

