Линейное уравнение первого и второго порядка

Введение

 

Актуальность этой темы заключается в том, что многие вопросы физики, химии, экономики, техники и других областей знаний сводятся к следующей задаче: найти функцию ¦¦, имея некоторые уравнения, в которое кроме этой функции и аргументов, от которых она зависит, входят также ее производные до некоторого порядка включительно. Такие уравнения называются дифференциальными уравнениями. Т.е. многие вопросы этих областей знаний решаются с помощью дифференциальных уравнений.

Уравнения, содержащие производные по многим независимым переменным, называются уравнения в частных производных. Уравнения, cодержащие производные лишь по одной из независимых переменных, называются обыкновенными дифференциальными уравнениями.

Независимую переменную, производная по которой входит в обыкновенное дифференциальное уравнение, обычно обозначают буквой x (или буквой t, поскольку во многих случаях роль независимой переменной играет время). Неизвестную функцию обозначают через y(x).

Обыкновенное дифференциальное уравнение можно записать в виде соотношения

 

 

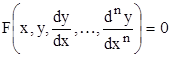
Порядок старшей производной, входящей в это уравнение называется порядком уравнения. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Целью данной дипломной работы является подготовка материалов для методического пособия по теории линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами.

Задачами исследования были: изучение и анализ линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами; рассмотрение свойств уравнений первого, второго и n-го порядков и свойств системы линейных уравнений; рассмотрение методов решения линейных однородны и неоднородных дифференциальных уравнений и применение их при решении физических задач, а также систем линейных дифференциальных уравнений..

Предметом исследования работы: являются линейные обыкновенных дифференциальные уравнения с постоянными коэффициентами и системы линейных уравнений.

Объектом исследования работы являются реальные процессы, описываемые данными дифференциальными уравнениями.

 

Линейное уравнение первого и второго порядка

ЛИНЕЙНОЕ УРАВНЕНИЕ n-го ПОРЯДКА

Доказательство.

Возьмём точку x = x₀ в которой , и составим систему линейных алгебраических уравнений относительно С₁,…, С_n с определением :

 

 (2.2.6)

 

Так как , то эта система имеет нетривиальное решение С₁, …, С_n. Рассмотрим линейную комбинацию

 

.

 

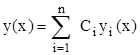Согласно теореме 1.4 у(x) является решением уравнения (2.2.1), а (2.2.6) означает, что это решение удовлетворяет в точке x₀ нулевым начальным условиям у(х₀) = 0,…, у^(n-1)(x₀) = 0. Так как тривиальное решение уравнения (2.2.1) удовлетворяет, очевидно, тем же начальным условиям, то, в силу теоремы единственности, у(x) (x)  0, т.е. 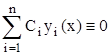, где по настроению не все С₁ равны нулю, а это и означает линейную зависимость у₁(x), …, у_n(x).Что и требовалось.

Из доказанных теорем непосредственно вытекает следующая альтернатива.

Теорема 2.3. Определитель Вронского D(x) либо тождественно равен нулю, и это означает, что решения у₁(x), …, y_n(x) линейно зависимы, либо не обращается в нуль ни в одной точке Х, и это означает, что у₁(x), …, y_n(x) линейно независимы.

Ситуацию можно выразить следующей схемой:

 

D(x)=

 

при любом x Х.

Определение. Фундаментальной системой решений уравнения (2.2.1) будем называть любые n линейно независимых решений уравнения (2.2.1)

Теорема 2.4. Линейное однородное уравнение имеет фундаментальную систему решений.

Доказательство.

Действительно, возьмём произвольный отличный от нуля определитель D⁰ с элементами . Определим решения у₁(x), …, у_n(x) уравнения (1.2.1) следующими начальными условиями:

 

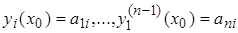 (4.7)

 

Составим определитель Вронского D(x). В силу (2.2.7) D(x₀) = D⁰ 0. А тогда, в силу теоремы 1.3, у₁(x), …, у_n(x) линейно независимы.

Замечание. Так как существует бесконечно много определителей, отличных от нуля, для каждого уравнения существует бесконечно много фундаментальных систем решений. Кроме того, линейное невырожденное преобразование

 

 

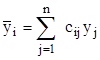
переводит одну фундаментальную систему решений в другую.

Докажем теперь основную теорему данного параграфа.

Теорема 2.5. Если у₁(x), …, у_n(x) - фундаментальная система решений, то любое решение у(x) уравнения (2.2.1) представимо в виде

 

, (2.2.8)

 

где С₁, …, С_n - некоторые постоянные.

Доказательство.

Пусть у(х₀) = у₁⁰, …, у^n-1(х₀) = у_n⁰. Определим постоянные С₁, …, С_n линейной системой уравнений с детерминантом, равным D(х₀)  0:

 

 (2.2.9)

 

и построим . Согласно теореме 1.4. (x) является решением уравнения (2.2.1), а (2.2.9) означает, что это решение удовлетворяет тем же начальным условиям, что и у(x). Тогда, в силу единственности,

 

.Что и требовалось.

Замечание. Формула (2.2.8), где С₁, …, С_n - произвольные постоянные, является общим решением уравнения (2.2.1), т.е. (2.2.8) является формулой, содержащей все решения уравнения (2.2.1) и не содержащей ничего, кроме решений. В самом деле, по теореме 1.4 при любых С₁, …, С_n (2.2.8) является решением уравнения (2.2.1), а согласно только что доказанной теореме в (2.2.8) содержится любое решение уравнения (2.2.1).

Замечание. На языке линейной алгебры теоремы 2.4 и 2.5 означают, что в пространстве решений линейного однородного уравнения (2.2.1) имеется базис из n элементов, т.е. это пространство n-мерное.

Доказательство.

Рассмотрим разность у(x)- 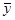(x). Согласно теореме 2.5 эта разность удовлетворяет однородному уравнению (2.2.1), и, значит, по теореме 1.5

 

 

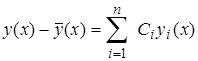
Отсюда и последует (2.3.2).

Таким образом, для построения общего решения неоднородного уравнения нужно помимо фундаментальной системы решений однородного уравнения узнать хотя бы одно частное решение неоднородного уравнения. Покажем сейчас, что зная фундаментальную систему решений, можно найти квадратурой некоторое частное решение 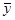(x) неоднородного уравнения.

Зададимся целью построить частное решение 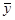(x), удовлетворяющее начальным условиям

 

у(х₀) = 0, …, у^(n-1)(х₀) = 0. (2.3.3)

 

С этой целью воспользуемся следующим эвристическим рассуждением. Представим f(x) приближённо как сумму функций (элементарных воздействий), равных f(x) в промежутке (x - Dx, x) и нулю в остальных точках. Решение у, отвечающее каждому такому элементарному воздействию, имеющее при x = x₀ равные нулю производные до (n-1)-го порядка включительно, является тождественным нулём вплоть до x-Dx, но

 

 

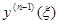
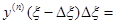
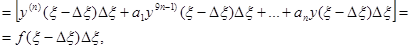
т.е. у^(n-1)(x) равно уже не нулю, а f(x)Dx и, таким образом, далее решение также будет не нулём. В силу принципа суперпозиции достаточно построить решение однородного уравнения (ведь вне (x - Dx, x) правая часть равна нулю), принимающее в точке x нулевое значение вместе с производными до(n-2)-го порядка включительно и с производной (n-1)-го порядка, равной единице (обозначим это решение 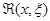, указывая зависимость от начальной точки, и назовём его импульсной функцией), а затем умножить его на f(x)Dx. Итак,  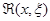строится как решение однородного уравнения, удовлетворяющее условиям

 

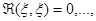
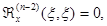
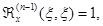 (2.3.4)

 

а решение, отвечающее элементарному воздействию, имеет вид 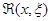f(x)Dx. Суммируя теперь элементарные воздействия на основании того же принципа суперпозиции и перехода от суммы к интегралу, получим решение, удовлетворяющее условию (2.3.3):

 

 

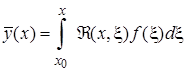. (2.3.5)

 

Формула (2.3.5) получена на основании эвристических соображений, но нетрудно непосредственной проверкой убедиться, что (2.3.5) есть частное решение уравнения (2.3.1). В этой проверке и будет состоять доказательство следующей теоремы:

Теорема 3.2. Выражение (2.3.5), где функция 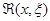, называемая импульсной функцией, удовлетворяет однородному уравнению (2.2.1) и начальным условиям (2.3.4), является частным решением неоднородного уравнения (2.3.1), удовлетворяющим нулевым начальным условиям (2.3.3).

Доказательство.

Найдём из (2.3.5) 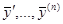. Предварительно заметим, что так как x является параметром, принадлежащим тому же множеству, что и x, то (2.3.4) равносильно записи

 

 

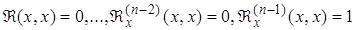
Дифференцируя (2.3.5), имеем

 

=

 

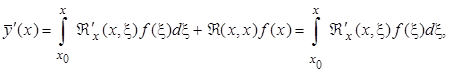
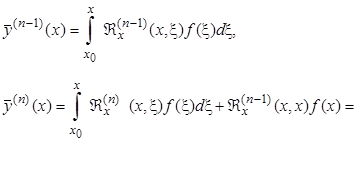
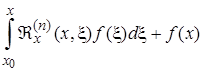
Возможность дифференцирования под знаком интеграла следует из теоремы о непрерывной зависимости решения системы дифференциальных уравнений от x и начального значения переменной x, т.е. в данном случае от x. Подставляя 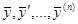 в (2.3.1), получим

 

 

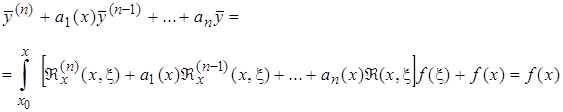
так как 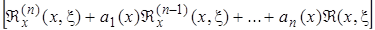под интегралом обращается в нуль в силу определения 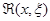. Таким образом,  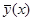действительно является решением уравнения (2.3.1) и, кроме того, очевидно, удовлетворяет (2.3.3).

Замечание. В частности, для уравнения первого порядка формула (2.3.5) совпадает с формулой (1.1.8) при у₀ = 0. В импульсной функцией (1.1.8) является множитель 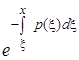, который согласно (1.1.5), удовлетворяет одному уравнению и обращается в единицу при x = x

Доказательство.

Это тождество доказывается непосредственным вычислением с использованием формулы Лейбница для дифференцирования произведения. Имеем

 

 

e^lxf=e^lxf

 

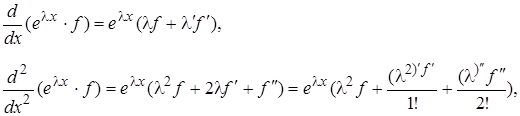
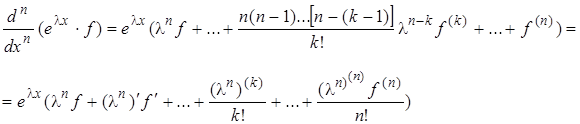
Складывая полученные равенства, умножив их предварительно на соответствующее а_i, приходим к (2.4.2). Что и требовалось.

Замечание. Если ,то (2.4.2) принимает вид

 

 (2.4.3)

Замечание. Тождества (2.4.2) - (2.4.4) можно записать компактнее, если обозначить через D оператор дифференцирования: . Если воспользоваться правилами сложения и умножения операторов, то левую часть уравнения (2.4.1) можно записать в виде

 

(Dⁿ + a₁D^n-1 + … + a_n)y = M(D)y.

 

Оператор M(D) называется операторным многочленом. Он имеет ту же структуру, что и характеристический многочлен M(l).

Введя M(D), можно тождества (2.4.2) - (2.4.4) записать в виде

(D)e^lxf(x)=e^lx (2.4.5)(D) e^lxx^p=e^lx (2.4.6)

M(D) e^lx=e^lxM(l). (2.4.7)

 

Отметим также следующее свойство операторных многочленов, которое понадобится в дальнейшем. Рассмотрим на ряду с M(D) некоторый другой операторный многочлен M(D). Пользуясь правилом сложения и умножения операторов, нетрудно убедиться, что операторные многочлены перемножаются по правилу обычных многочленов:

(D)N(D) = N(D)M(D) = D^n+s +(a₁+b₁)D^n+s+1 + … +а_nb_n.

 

Приравнивая M(l) нулю, получим алгебраическое уравнение n-й степени относительно l - так называемое характеристическое уравнение

 

lⁿ + а₁l^n-1 + … + а_n = 0. (2.4.8)

 

Предположим, что это уравнение имеет корни l₁, …, l_l кратностей m₁…, m_l (m₁ + … + m_l = n).

Теорема 4.1.1. Корню l_k характеристического уравнения (2.4.8) кратности m_k, отвкчают m_k частных решений вида

 

 (2.4.9)

 

2 Решения (2.4.9), где k=1,..., l, образуют фундаментальную систему решений уравнения (2.4.1).

Доказательство.

Воспользуемся (2.4.3) или (2.4.6). Если l_k является корнем характеристического уравнения кратности m_k, то

 

M(l_k)= M¹ (l_k)=…=M^(m_k^{- 1)} (l_k)=0

 

Поэтому правая часть (2.4.3) обращается в нуль для p=0,1,.., m_k-1, а это означает, что x^pe^l_k^x (p=0,1…, m_k-1) удовлетворяет уравнению (2.4.1), что и требуется.

2. Предположим противное, т.е., что решение (2.4.9) (k=1,…,l) линейно зависимы. Это означает, что справедливо тождество

 

R₁ (x) e^l₁^x +…+ R_l (х) e^l_l^x = 0 (2.4.10)

 

через R_j(x) обозначены многочленные степени m_j-1, не все равные нулю. Допустим, что отличным от нуля является R₁ (этого можно добиться соответствующей нумерацией l), а в R₁ старший отличный от нуля член имеет степень p₁(p₁ m₁-1), т.е.

 

R₁(x) = C₁₀ + C₁₁x + … C_1p1 x^p1,

 

причем С_1р1 0.

Умножим (6.10) на е^-l_l ^Х. Получим

 

R₁(х) е^(l₁^{- l}_l^)х + … + R_l-1 (x) e^(l_l-1^{- l}_l^{) х l} + R_l (x) = 0. (2.4.11)

 

Продифференцируем это тождество на единицу большее число раз, нежели степень p_l = m_l-1 многочлена R_l(x). Предварительно заметим, что для выражения А(x) е^ax где a = const, А(x)- многочлен, при произвольном k имеет место тождество

 

,

 

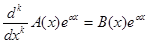где В(х) - многочлен той же степени, что и А(x), причем его старший коэффициент равен старшему коэффициенту А(х), помноженному на a^k. Это тождество легко получить либо из (2.4.5), полагая M(D)=D^k, l=a, ƒ(x)=A(x), либо просто из формулы Лейбница. Итак, дифференцируя (2.4.11) получим

 

Q₁(x)e^(l₁^{- l}_l^)x+…Q_l-1(x)e ^(l_l-1^{- l}_l^)x =0,

 

или

 

Q₁(x)e ^l_l^x+…+Q_l-1(x)e ^l_l-1^x =0, (2.4.12)

 

где Q₁(x),…, Q_l-1(x)- многочлены той же степени, что R₁,…,R_l-1, причем коэффициент старшего члена Q₁(x) есть C_1pl(l1- ll)^p_l⁺¹_. Проделывая с (2.4.12) ту же операцию, что и с (2.4.10), и продолжая этот процесс, приходим к тождеству вида

 

S₁(x)e^l₁^x=0 или S₁(x)=0, (2.4.13)

 

причем коэффициент старшего члена S₁(x) есть C_1pl(l1- ll)^p_l+1…(l₁- l₂)^p_l+1 и в силу (2.4.13) он должен равняться нулю, а это противоречит тому, что С _1р1  0, l₁-l_l 0,…,l₁-l₂ 0. Противоречие приводит к выводу, что решение (2.4.9) линейно независимы, т.е. образуют фундаментальную систему решений, и утверждение 2, таким образом, доказано.

В силу теоремы 4.1 общее решение уравнения 2.4.1 является линейной комбинацией решений (2.4.9) (k-1,…,l). Однако в случае комплексных l_k такое представление не всегда удобно. Можно, однако, вместо фундаментальной системы решений (2.4.9) пользоваться другой фундаментальной системой решений, состоящих из действительных функций.

Пусть l_k=p_k+iq_k. Тогда двум комплексным решениям вида x^r e^l_k^X, соответствуют, в силу теоремы 1.6, два действительных решения:

 

 

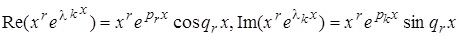
Таким образом, вместо комплексных решений можно построить столько же действительных решений; они образуют другую фундаментальную систему решений, будучи линейно независимы в силу того, что матрица перехода от пары комплексно сопряженных решений к их действительной и мнимой частям имеет вид 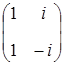 и имеет отличный от нуля определитель, равный

Беря линейную комбинацию полученных действительных решений, приходим к представлению (1.2.25), которое теперь, таким образом доказана.

Рассмотрим теперь неоднородное уравнение

 

 (2.4.14)

 

Зная фундаментальную систему решений (2.4.9), можно построить его частное решение по теореме 3.2. Практически это, однако, требует довольно громоздких выкладок, в связи с чем представляет интерес класс , для которого можно построить частное решение, не обращаясь к формуле (2.3.5), а пользуясь чисто алгебраическими операциями.

Теорема 4.2. Пусть многочлен степени s. Пусть l не совпадает не с одним корнем l_k характеристического уравнения (2.4.8) (так называемый нерезонансный случай). Тогда существует частное решение уравнения (2.4.14), имеющее вид

 

, (2.4.15)

 

где P(x)- многочлен той же степени, что и S(x).

Если l не совпадает с корнем характеристического уравнения l_k кратности m_k (так называемый резонансный случай), то существует частная решение уравнения (2.4.14), имеющее вид

 

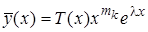, (2.4.16)

 

где Т(x) - многочлен той же степени, что и S(x).

На основании этой теоремы частное решение ищется в указанном виде, где многочлен P(x) или Т(x) записывается с неизвестными коэффициентами. Подставляя в уравнение (2.4.14), сокращая на 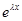 и приравнивая члены с одинаковыми степенями x, получим систему неоднородных алгебраических уравнений относительно неизвестных коэффициентов многочлена Р(x) или Т(x). Эта система будет разрешимой, поскольку существование решения такого вида обеспечена теоремой 4.2.

Доказательство.

Доказательство приведем для резонансного случая (2.4.16), так как (2.4.15) получается их (2.4.16) при m_k =0. Подставим (2.4.16) в (2.4.14):

 

 (2.4.17)

 

и убедимся, что отсюда можно определить последовательно коэффициенты многочлена Т(x), начиная с коэффициента при старшей степени x^s. Выделим в многочленах Т(x) и S(x) старшие члены:

 

 

Имеем тогда

 

 

Распишем первое слагаемое слева, пользуясь формулой (2.4.6) и учитывая, что  Получим

 

 (2.4.18)

 

Заметим, что в выражении стоящем в фигурных скобках, первая слагаемая имеет степень s, а прочие- более низкую. Приравнивая старшие члены и сокращая на будем иметь

 

 

Отсюда определиться b₀ через в силу  После этого (2.4.18) можно записать в виде

 

 (2.4.19)

 

где 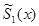- многочлен в степени не выше s-1, полученный в результате перенесения в право всех членов выражения 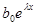умноженного на выражение состоящее в фигурных скобках (кроме первого), который теперь известен.

Соотношение (2.4.19) представляет собой уравнение, аналогичное (2.4.17), но степени многочленов и 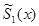на единицу ниже и. Из (2.4.19) аналогична предыдущему определиться старший коэффициент многочлена , т.е. определяться уже два старших члена многочлена . Продолжая процесс, определим последовательно все члены .

Метод отыскания частного решения, основанный на доказанной теореме, будем называть методом неопределенных коэффициентов.

Итак, для уравнения с постоянными коэффициентами фундаментальная система решений, а в случае правой части вида 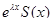также и частное решение неоднородного уравнения могут быть построены в эффективной форме путем алгебраических операций. В заключение укажем один специальный класс уравнений с переменными коэффициентами, для которого фундаментальную систему решений также можно построить эффективно. Это так называемое уравнение Эйлера.

 

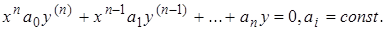 (2.4.20)

 

Непосредственной выкладкой нетрудно убедиться, что заменой независимого переменного уравнение (2.4.20) сводится к уравнению с постоянными коэффициентами, что и решает вопрос об эффективном построении фундаментальной системы решений.

Для отыскания частного решения неоднородного уравнения Эйлера в случае, если правая часть имеет вид , применим метод неопределенных коэффициентов.

 

Системы линейных уравнений

 

Обратимся к изучений системы линейных дифференциальных уравнений

 

 (3.1.1)

 

Система (3.1.1) называется однородной, если ¦ _i (x) = 0 (i = 1, …, n) в противном случае - неоднородной. Будем предполагать a_ik(x) и ¦_i(x) непрерывными на интервале X. Как было доказано выше, при этих условиях на Х существует единственное решение системы (3.1.1), удовлетворяющее начальному условию

_i(x₀) = 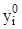, i = 1, …, n. (3.1.2)

 

Для системы уравнений справедливы теоремы, аналогичные тем, которые были доказаны для одного уравнения n-го порядка.

Общие свойства системы линейных уравнений. Обратимся системе (3.1.1). Обозначим через у, ¦ и y⁰ столбцы

 

 

 

а через А (х) обозначим (n ´ n) - матрицу с элементами а_ij(х):

 

 

Тогда систему (3.1.1) можно записать в виде одного уравнения

' = A (x) y + f {x), (3.1.3)

 

точно так же, как и начальные условия

 (x₀) = y⁰. (3.1.4)

 

Пользуясь правилом умножения 4°, правилом сложения3° иправилом равенства матриц 2°, нетрудно убедиться в том, что (3.1.3) и (3.1.4) то же самое, что и (3.1.1) и (3.1.2).

В силу свойств умножения и дифференцирования матриц для дифференцируемых столбцов имеет место тождество, в котором a_i - постоянные числа,

 

 (3.1.5)

 

выражающее свойство линейности оператора y¢ - Ay º L[y] на множестве дифференцируемых столбцов.

Здесь и в дальнейшем для нумерации столбцов будем употреблять индекс, заключенный в круглые скобки, оставляя индекс без скобок для обозначения элементов (компонент).

Непосредственным следствием этого тождества является принцип суперпозиции.

Теорема 3.1.1. Пусть в уравнении (3.1.3) f (x) является линейной комбинацией f _(i)(х),т.е.

 

 

где a_i - постоянные числа, и пусть y_(i)(x)является решением уравненияy'_(i) = A(x) y_(i) + f _(i).

Тогда линейная комбинация y_(i) (x) с теми же коэффициентамиa_i, т.е. столбец у (х) = ,является решением уравнения (3.1.3).

Имеют также место теоремы, аналогичные теоремам 1.4-1.6.

Однородное уравнение. Рассмотрим более детально однородное уравнение

 

у ' = А (х) у. (3.1.6)

 

Пусть имеется п столбцов

 

 

Составим из этих столбцов матрицу W(x):

 

 (3.1.7)

 

Сопоставим уравнению (3.1.6), правая и левая части которого - столбцы, аналогичное уравнение

¢ = A (x) W, (3.1.8)

 

правая и левая части которого - матрицы размерности (n ´ n)и в котором неизвестной является матрица W(x).

Теорема 3.1.2. Пусть y₍₁₎,..., у_(n) есть n решений уравнения (3.1.6). Тогда (n ´ n) - матрица W(x), образованная из них по формуле (3.1.7), является решением матричного уравнения (3.1.8).

Обратно: если W(x) является решением уравнения (3.1.8), то каждый столбец матрицы W(x) является решением уравнения (3.1.6).

Доказательство. Достаточно расписать (3.1.8) и (3.1.6) поэлементно. Действительно, (3.1.8) означает

 

 (3.1.9)

 

или

 

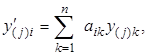 (3.1.10)

 

 

a (3.1.6) означает

 

 (3.1.11)

 

Поэтому если у_(j) являются решениями (3.1.6), то каждое у_(j) удовлетворяет (3.1.11), т.е. справедливо (3.1.10) или, что то же, (3.1.9), а значит, и (3.1.8), и наоборот, если справедливо (3.1.8), то и (3.1.10), а это в сопоставлении с (3.1.11) означает, что у_(j) (j = 1,..., n) является решением уравнения (3.1.6).

Отметим еще следующие факты, проверяемые столь же просто.

Теорема 3.1.3. Если W(x) - решение уравнения (3.1.8), то выражение WB является решением уравнения (3.1.6), если В - произвольный постоянный столбец, и решением уравнения (3.1.8), если В - произвольная постоянная (n ´ n) - матрица.

Определение. Будем говорить, что столбцы u_(i),..., u_(р) линейно зависимы на интервале X, если существуют постоянные C₁,..., С_р, не все равные нулю, такие, что имеет место тождество

 

 (3.1.12)

 

Если же (3.1.12) выполняется только при C₁ =... = С_р = 0, то будем говорить, что u₍₁₎, …, u_(p) линейно независимы.

Рассмотрим n дифференцируемых столбцов у₍₁₎,..., у_(n). Запишем для них равенство (3.1.12):

 

 

 (3.1.13)

 

Введем в рассмотрение постоянный столбец 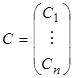. Пользуясь этим столбцом и матрицей W(x}, составленной из у_(i) по правилу (3.1.7), можно (3.1.13) записать в виде

 = 0. (3.1.14)

 

Так как, согласно правилу матричного исчисления, 2° считается С = 0, если все С_i (i = 1,..., n) равны нулю, то определение линейной зависимости и независимости у_(i), …, y_(n) можно сформулировать следующим образом.

Определение. Будем говорить, что столбцы y₍₁₎,..., y_(n) линейно зависимы на интервале X, если существует постоянный столбец C ¹ 0 такой, что тождественно на Х имеет место (3.1.14).

В противном случае, т.е. если (3.1.14) справедливо только при С = 0, будем говорить, что y₍₁₎,..., y_(n) линейно независимы.

Определение. Назовем ∆(x) = Det W(x) определителем Вронского для y₍₁₎,..., y_(n).

Теперь можно сформулировать и доказать теоремы, аналогичные теоремам 1.7 - 1.9 из теории уравнения n-го порядка. Все эти доказательства записываются весьма компактно, если пользоваться введенной матричной записью, которая очень удобна и требует лишь некоторого навыка.

Теорема 3.1.4. Если решения y₍₁₎,..., y_(n) уравнения (3.1.6) линейно зависимы на X, то ∆(x) º 0 на X.

Доказательство.

Имеем WC = 0, С ¹ 0. Эта запись является кратким обозначением того факта, что при каждом х величины C₁,..., С_n удовлетворяют системе линейных алгебраических уравнений с определителем ∆ (x), и так как решение нетривиальное, то ∆ (x) = 0 при любом х Î X, т.е. ∆(x} º 0.

Теорема 3.1.5. Если ∆ (x) = 0 хотя бы для одного х₀ Î X, то, решения y₍₁₎,..., y_(n) уравнения (3.1.6) линейно зависимы на Г.

Доказательство.

Запишем кратко доказательство этой теоремы, уже не давая дополнительных разъяснений, как в предыдущей. Возьмем x₀ Î X, и пусть, ∆ (x₀) = 0. Составим уравнение W(x₀) C = 0 относительно С. В силу ∆ (x₀) = 0 существует решение С ¹ О. Положим у (x) = W (x) С. Согласно теореме 3.1.3 это решение уравнения (3.1.6), причем y (x₀) = W (x₀) C = 0, а тогда, в силу теоремы единственности, y (x) º 0 и, таким образом, W (х) С º 0, что, означает линейную зависимость y₍₁₎,..., y_(n).

Теорема 3.1.6. (альтернатива). Определитель Вронского либо тождественно равен нулю, и это означает, что решения y₍₁₎,..., y_(n) линейно зависимы, либо не обращается в нуль ни в одной точке X, и это означает, что решения y₍₁₎,..., y_(n) линейно независимы.

Определение. Фундаментальной системой решений уравнения (3.1.6) будем называть n линейно независимых решений y₍₁₎,..., y_(n) уравнения (3.1.6), а соответствующую им по формуле (3.1.7) матрицу W{x) будем называть фундаментальной матрицей.

На основании теоремы 3.1.5. можно дать другое (эквивалентное) определение фундаментальной матрицы.

Определение. Решение W(x) уравнения (3.1.8), для которого ∆(х} отлично от нуля всюду на X, называется фундаментальной матрицей.

Теорема 3.1.7. Линейная однородная система уравнений имеет фундаментальную матрицу.

В силу теоремы 3.1.6. достаточно взять произвольную матрицу а = const с отличным от пуля определителем и задать для W начальное условие W (x₀) = a.

Теорема 3.1.8. Если W (x) - фундаментальная матрица, то любое решение у(х) уравнения (3.1.6) представимо в виде

 (x) = W (x) C, (3.1.15)

 

где С - некоторый постоянный столбец.

Доказательство.

Пусть y (x₀) = y⁰. Определим С уравнением W (x₀) C = у⁰, которое разрешимо в силу ∆ (x₀) ¹ 0. Построим (х) = W (x) C. Так как  (x_о) = W(x₀) C = y⁰, то в силу теоремы единственности у (х) º 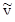 (х) = W (x) C, что и требовалось.

Замечание. На языке линейной алгебры теоремы 3.1.7. и 3.1.8. означают, что, пространство решений уравнения (3.1.6) n-мерно.

Построим решение уравнения (3.1.6), удовлетворяющее условиям (3.1.4), выразив с помощью W (x) величину С через у⁰. Имеем

(x₀) = W (x₀) C = y⁰,

 

откуда

 

С = W^{- 1} (x₀) у⁰

и, следовательно,

 

y (x) = W (x) W^{- 1} (x₀) y⁰.

 

Матрицу Â (х, х₀) = W (х) W^{- 1} (х₀), являющуюся функцией двух переменных х и x₀, назовем импульсной матрицей, или матрицантом. В силу теоремы 3.1.3. Â (х, х₀) как функция х удовлетворяет уравнению (3.1.8). Кроме того, очевидно, что

 

 (х, х₀) = E.

 

Таким образом, справедлива

Теорема 3.1.9. Решение задачи (3.1.6), (3.1.4) имеет вид

 (x) = Â (x, x₀) y⁰, (3.1.16)

 

где матрица Â (х, x₀) удовлетворяет по аргументу х матричному уравнению (3.1.8) и условию Â (х, x₀) = Е.

Неоднородное уравнение. Рассмотрим теперь неоднородное уравнение (3.1.3).

Теорема 3.1.10. Если W (х) - фундаментальная матрица, а  (х) - частное решение неоднородного уравнения (3.1.3), то любое решение у (х) уравнения (3.1.3) представило в виде

 (x) = W (x) C +  (x), (3.1.17)

 

где С - некоторый постоянный столбец.

Доказательство точно такое же, как в случае уравнения n-го порядка, и мы его опускаем.

Построим частное решение  (х), удовлетворяющее нулевым начальным условиям (x₀) = 0. Будем искать его в виде

 

 (x) = W (x) C (x),

 

где С (x)-неизвестный столбец. Это фактически просто замена переменных. Подставляя  (х) в (3.1.3), получим

 

 

W' C + W C' = AWC + f.

 

Так как W удовлетворяет (3.1.8), то W¢ - AW = 0 и, следовательно, WC' = f. Отсюда C' = W^{- 1} f. А так как 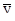 (x₀) = W(x₀) C(x₀) = 0, то С (х₀) = 0 и, следовательно,

 

 

Таким образом,

 

 

и справедлива

Теорема 3.1.11. Частное решение 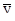(х)'уравнения (3.1.3), удовлетворяющее условию 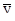(х₀) = 0, имеет вид

 

 (3.1.18)

 

где Â (х, x) - импульсная матрица, или матрицант, - решение матричного уравнения (3.1.8), удовлетворяющее условию Â (x, x) = E.

Замечания. 1. Изложенный метод построения частного решения системы линейных уравнений фактически является вариантом метода вариации постоянных, который для одного уравнения использовался в гл. 1. п. 1.1.

2. В силу принципа суперпозиции решен