Линейное уравнение n-го порядка с постоянными коэффициентами

Знание фундаментальной системы решений обеспечивает возможность найти любое решение однородного уравнения, а с применением квадратуры - также и решение неоднородного уравнения. Существование фундаментальной системы решений было доказано в теореме 2.4, однако вопрос о её эффективном построении остался открытым.

Пусть в (2.2.1)

 

а_i = соnst:

у⁽ⁿ⁾ + a₁у^(n-1) + … + а_ny = 0. (2.4.1)

 

Этот класс уравнений замечателен тем, что для него нахождения фундаментальной системы решений сводится к алгебраическим операциям, а именно к решению алгебраического уравнения n-ой степени.

Сопоставим уравнению (2.4.1) многочлен относительно l, называемый характеристическим многочленом уравнения (2.4.1):

(l)=lⁿ+a₁l^n-1+...+a_n..

Лемма 4.1. Справедлтво тождество

 

 (2.4.2.)

Доказательство.

Это тождество доказывается непосредственным вычислением с использованием формулы Лейбница для дифференцирования произведения. Имеем

 

 

e^lxf=e^lxf

 

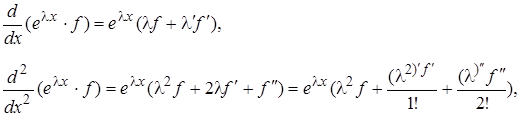
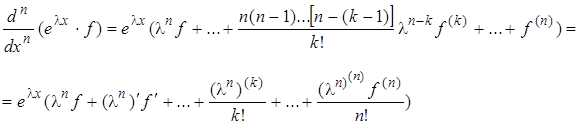
Складывая полученные равенства, умножив их предварительно на соответствующее а_i, приходим к (2.4.2). Что и требовалось.

Замечание. Если ,то (2.4.2) принимает вид

 

 (2.4.3)

Замечание. Тождества (2.4.2) - (2.4.4) можно записать компактнее, если обозначить через D оператор дифференцирования: . Если воспользоваться правилами сложения и умножения операторов, то левую часть уравнения (2.4.1) можно записать в виде

 

(Dⁿ + a₁D^n-1 + … + a_n)y = M(D)y.

 

Оператор M(D) называется операторным многочленом. Он имеет ту же структуру, что и характеристический многочлен M(l).

Введя M(D), можно тождества (2.4.2) - (2.4.4) записать в виде

(D)e^lxf(x)=e^lx (2.4.5)(D) e^lxx^p=e^lx (2.4.6)

M(D) e^lx=e^lxM(l). (2.4.7)

 

Отметим также следующее свойство операторных многочленов, которое понадобится в дальнейшем. Рассмотрим на ряду с M(D) некоторый другой операторный многочлен M(D). Пользуясь правилом сложения и умножения операторов, нетрудно убедиться, что операторные многочлены перемножаются по правилу обычных многочленов:

(D)N(D) = N(D)M(D) = D^n+s +(a₁+b₁)D^n+s+1 + … +а_nb_n.

 

Приравнивая M(l) нулю, получим алгебраическое уравнение n-й степени относительно l - так называемое характеристическое уравнение

 

lⁿ + а₁l^n-1 + … + а_n = 0. (2.4.8)

 

Предположим, что это уравнение имеет корни l₁, …, l_l кратностей m₁…, m_l (m₁ + … + m_l = n).

Теорема 4.1.1. Корню l_k характеристического уравнения (2.4.8) кратности m_k, отвкчают m_k частных решений вида

 

 (2.4.9)

 

2 Решения (2.4.9), где k=1,..., l, образуют фундаментальную систему решений уравнения (2.4.1).

Доказательство.

Воспользуемся (2.4.3) или (2.4.6). Если l_k является корнем характеристического уравнения кратности m_k, то

 

M(l_k)= M¹ (l_k)=…=M^(m_k^{- 1)} (l_k)=0

 

Поэтому правая часть (2.4.3) обращается в нуль для p=0,1,.., m_k-1, а это означает, что x^pe^l_k^x (p=0,1…, m_k-1) удовлетворяет уравнению (2.4.1), что и требуется.

2. Предположим противное, т.е., что решение (2.4.9) (k=1,…,l) линейно зависимы. Это означает, что справедливо тождество

 

R₁ (x) e^l₁^x +…+ R_l (х) e^l_l^x = 0 (2.4.10)

 

через R_j(x) обозначены многочленные степени m_j-1, не все равные нулю. Допустим, что отличным от нуля является R₁ (этого можно добиться соответствующей нумерацией l), а в R₁ старший отличный от нуля член имеет степень p₁(p₁ m₁-1), т.е.

 

R₁(x) = C₁₀ + C₁₁x + … C_1p1 x^p1,

 

причем С_1р1 0.

Умножим (6.10) на е^-l_l ^Х. Получим

 

R₁(х) е^(l₁^{- l}_l^)х + … + R_l-1 (x) e^(l_l-1^{- l}_l^{) х l} + R_l (x) = 0. (2.4.11)

 

Продифференцируем это тождество на единицу большее число раз, нежели степень p_l = m_l-1 многочлена R_l(x). Предварительно заметим, что для выражения А(x) е^ax где a = const, А(x)- многочлен, при произвольном k имеет место тождество

 

,

 

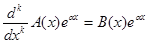где В(х) - многочлен той же степени, что и А(x), причем его старший коэффициент равен старшему коэффициенту А(х), помноженному на a^k. Это тождество легко получить либо из (2.4.5), полагая M(D)=D^k, l=a, ƒ(x)=A(x), либо просто из формулы Лейбница. Итак, дифференцируя (2.4.11) получим

 

Q₁(x)e^(l₁^{- l}_l^)x+…Q_l-1(x)e ^(l_l-1^{- l}_l^)x =0,

 

или

 

Q₁(x)e ^l_l^x+…+Q_l-1(x)e ^l_l-1^x =0, (2.4.12)

 

где Q₁(x),…, Q_l-1(x)- многочлены той же степени, что R₁,…,R_l-1, причем коэффициент старшего члена Q₁(x) есть C_1pl(l1- ll)^p_l⁺¹_. Проделывая с (2.4.12) ту же операцию, что и с (2.4.10), и продолжая этот процесс, приходим к тождеству вида

 

S₁(x)e^l₁^x=0 или S₁(x)=0, (2.4.13)

 

причем коэффициент старшего члена S₁(x) есть C_1pl(l1- ll)^p_l+1…(l₁- l₂)^p_l+1 и в силу (2.4.13) он должен равняться нулю, а это противоречит тому, что С _1р1  0, l₁-l_l 0,…,l₁-l₂ 0. Противоречие приводит к выводу, что решение (2.4.9) линейно независимы, т.е. образуют фундаментальную систему решений, и утверждение 2, таким образом, доказано.

В силу теоремы 4.1 общее решение уравнения 2.4.1 является линейной комбинацией решений (2.4.9) (k-1,…,l). Однако в случае комплексных l_k такое представление не всегда удобно. Можно, однако, вместо фундаментальной системы решений (2.4.9) пользоваться другой фундаментальной системой решений, состоящих из действительных функций.

Пусть l_k=p_k+iq_k. Тогда двум комплексным решениям вида x^r e^l_k^X, соответствуют, в силу теоремы 1.6, два действительных решения:

 

 

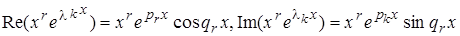
Таким образом, вместо комплексных решений можно построить столько же действительных решений; они образуют другую фундаментальную систему решений, будучи линейно независимы в силу того, что матрица перехода от пары комплексно сопряженных решений к их действительной и мнимой частям имеет вид 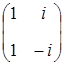 и имеет отличный от нуля определитель, равный

Беря линейную комбинацию полученных действительных решений, приходим к представлению (1.2.25), которое теперь, таким образом доказана.

Рассмотрим теперь неоднородное уравнение

 

 (2.4.14)

 

Зная фундаментальную систему решений (2.4.9), можно построить его частное решение по теореме 3.2. Практически это, однако, требует довольно громоздких выкладок, в связи с чем представляет интерес класс , для которого можно построить частное решение, не обращаясь к формуле (2.3.5), а пользуясь чисто алгебраическими операциями.

Теорема 4.2. Пусть многочлен степени s. Пусть l не совпадает не с одним корнем l_k характеристического уравнения (2.4.8) (так называемый нерезонансный случай). Тогда существует частное решение уравнения (2.4.14), имеющее вид

 

, (2.4.15)

 

где P(x)- многочлен той же степени, что и S(x).

Если l не совпадает с корнем характеристического уравнения l_k кратности m_k (так называемый резонансный случай), то существует частная решение уравнения (2.4.14), имеющее вид

 

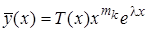, (2.4.16)

 

где Т(x) - многочлен той же степени, что и S(x).

На основании этой теоремы частное решение ищется в указанном виде, где многочлен P(x) или Т(x) записывается с неизвестными коэффициентами. Подставляя в уравнение (2.4.14), сокращая на 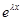 и приравнивая члены с одинаковыми степенями x, получим систему неоднородных алгебраических уравнений относительно неизвестных коэффициентов многочлена Р(x) или Т(x). Эта система будет разрешимой, поскольку существование решения такого вида обеспечена теоремой 4.2.

Доказательство.

Доказательство приведем для резонансного случая (2.4.16), так как (2.4.15) получается их (2.4.16) при m_k =0. Подставим (2.4.16) в (2.4.14):

 

 (2.4.17)

 

и убедимся, что отсюда можно определить последовательно коэффициенты многочлена Т(x), начиная с коэффициента при старшей степени x^s. Выделим в многочленах Т(x) и S(x) старшие члены:

 

 

Имеем тогда

 

 

Распишем первое слагаемое слева, пользуясь формулой (2.4.6) и учитывая, что  Получим

 

 (2.4.18)

 

Заметим, что в выражении стоящем в фигурных скобках, первая слагаемая имеет степень s, а прочие- более низкую. Приравнивая старшие члены и сокращая на будем иметь

 

 

Отсюда определиться b₀ через в силу  После этого (2.4.18) можно записать в виде

 

 (2.4.19)

 

где 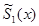- многочлен в степени не выше s-1, полученный в результате перенесения в право всех членов выражения 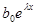умноженного на выражение состоящее в фигурных скобках (кроме первого), который теперь известен.

Соотношение (2.4.19) представляет собой уравнение, аналогичное (2.4.17), но степени многочленов и 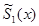на единицу ниже и. Из (2.4.19) аналогична предыдущему определиться старший коэффициент многочлена , т.е. определяться уже два старших члена многочлена . Продолжая процесс, определим последовательно все члены .

Метод отыскания частного решения, основанный на доказанной теореме, будем называть методом неопределенных коэффициентов.

Итак, для уравнения с постоянными коэффициентами фундаментальная система решений, а в случае правой части вида 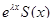также и частное решение неоднородного уравнения могут быть построены в эффективной форме путем алгебраических операций. В заключение укажем один специальный класс уравнений с переменными коэффициентами, для которого фундаментальную систему решений также можно построить эффективно. Это так называемое уравнение Эйлера.

 

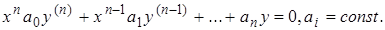 (2.4.20)

 

Непосредственной выкладкой нетрудно убедиться, что заменой независимого переменного уравнение (2.4.20) сводится к уравнению с постоянными коэффициентами, что и решает вопрос об эффективном построении фундаментальной системы решений.

Для отыскания частного решения неоднородного уравнения Эйлера в случае, если правая часть имеет вид , применим метод неопределенных коэффициентов.