Рассмотрим теперь уравнение
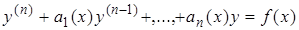 (2.3.1)
(2.3.1)
где 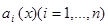 непрерывны на интервале X.
непрерывны на интервале X.
Теорема 3.1 Если у1(x), …, уn(x) - фундаментальная система решений однородного уравнения (4.1), а 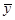 (x) - частное решение неоднородного уравнения (2.3.1), то любое решение у(x) неоднородного уравнения (2.3.1) представляется в виде
(x) - частное решение неоднородного уравнения (2.3.1), то любое решение у(x) неоднородного уравнения (2.3.1) представляется в виде
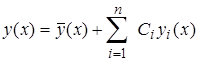 (2.3.2)
(2.3.2)
где С1, …, Сn некоторые постоянные.
Замечание. Теорема справедлива при любом выборе частного решения 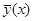 .
.
Замечание. Теорему 3.1 можно сформулировать и так: общее решение неоднородного уравнения есть сумма частного решения неоднородного уравнения и общего решения однородного уравнения.
Доказательство.
Рассмотрим разность у(x)- 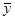 (x). Согласно теореме 2.5 эта разность удовлетворяет однородному уравнению (2.2.1), и, значит, по теореме 1.5
(x). Согласно теореме 2.5 эта разность удовлетворяет однородному уравнению (2.2.1), и, значит, по теореме 1.5
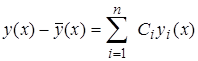
Отсюда и последует (2.3.2).
Таким образом, для построения общего решения неоднородного уравнения нужно помимо фундаментальной системы решений однородного уравнения узнать хотя бы одно частное решение неоднородного уравнения. Покажем сейчас, что зная фундаментальную систему решений, можно найти квадратурой некоторое частное решение 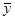 (x) неоднородного уравнения.
(x) неоднородного уравнения.
Зададимся целью построить частное решение 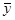 (x), удовлетворяющее начальным условиям
(x), удовлетворяющее начальным условиям
у(х0) = 0, …, у(n-1)(х0) = 0. (2.3.3)
С этой целью воспользуемся следующим эвристическим рассуждением. Представим f(x) приближённо как сумму функций (элементарных воздействий), равных f(x) в промежутке (x - Dx, x) и нулю в остальных точках. Решение у, отвечающее каждому такому элементарному воздействию, имеющее при x = x0 равные нулю производные до (n-1)-го порядка включительно, является тождественным нулём вплоть до x-Dx, но
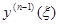
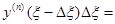

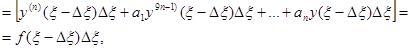
т.е. у(n-1)(x) равно уже не нулю, а f(x)Dx и, таким образом, далее решение также будет не нулём. В силу принципа суперпозиции достаточно построить решение однородного уравнения (ведь вне (x - Dx, x) правая часть равна нулю), принимающее в точке x нулевое значение вместе с производными до(n-2)-го порядка включительно и с производной (n-1)-го порядка, равной единице (обозначим это решение 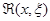 , указывая зависимость от начальной точки, и назовём его импульсной функцией), а затем умножить его на f(x)Dx. Итак,
, указывая зависимость от начальной точки, и назовём его импульсной функцией), а затем умножить его на f(x)Dx. Итак, 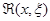 строится как решение однородного уравнения, удовлетворяющее условиям
строится как решение однородного уравнения, удовлетворяющее условиям
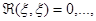
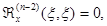
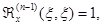 (2.3.4)
(2.3.4)
а решение, отвечающее элементарному воздействию, имеет вид 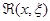 f(x)Dx. Суммируя теперь элементарные воздействия на основании того же принципа суперпозиции и перехода от суммы к интегралу, получим решение, удовлетворяющее условию (2.3.3):
f(x)Dx. Суммируя теперь элементарные воздействия на основании того же принципа суперпозиции и перехода от суммы к интегралу, получим решение, удовлетворяющее условию (2.3.3):
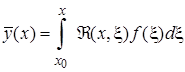 . (2.3.5)
. (2.3.5)
Формула (2.3.5) получена на основании эвристических соображений, но нетрудно непосредственной проверкой убедиться, что (2.3.5) есть частное решение уравнения (2.3.1). В этой проверке и будет состоять доказательство следующей теоремы:
Теорема 3.2. Выражение (2.3.5), где функция 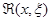 , называемая импульсной функцией, удовлетворяет однородному уравнению (2.2.1) и начальным условиям (2.3.4), является частным решением неоднородного уравнения (2.3.1), удовлетворяющим нулевым начальным условиям (2.3.3).
, называемая импульсной функцией, удовлетворяет однородному уравнению (2.2.1) и начальным условиям (2.3.4), является частным решением неоднородного уравнения (2.3.1), удовлетворяющим нулевым начальным условиям (2.3.3).
Доказательство.
Найдём из (2.3.5) 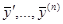 . Предварительно заметим, что так как x является параметром, принадлежащим тому же множеству, что и x, то (2.3.4) равносильно записи
. Предварительно заметим, что так как x является параметром, принадлежащим тому же множеству, что и x, то (2.3.4) равносильно записи
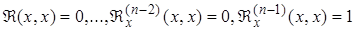
Дифференцируя (2.3.5), имеем
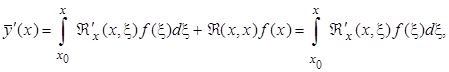
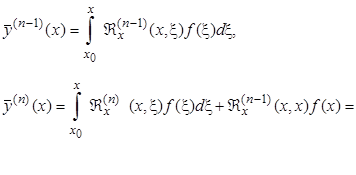
= 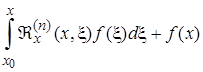
Возможность дифференцирования под знаком интеграла следует из теоремы о непрерывной зависимости решения системы дифференциальных уравнений от x и начального значения переменной x, т.е. в данном случае от x. Подставляя 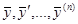 в (2.3.1), получим
в (2.3.1), получим
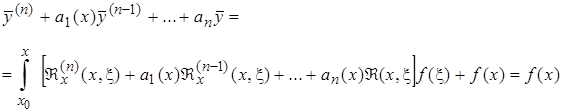
так как 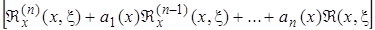 под интегралом обращается в нуль в силу определения
под интегралом обращается в нуль в силу определения 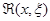 . Таким образом,
. Таким образом, 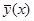 действительно является решением уравнения (2.3.1) и, кроме того, очевидно, удовлетворяет (2.3.3).
действительно является решением уравнения (2.3.1) и, кроме того, очевидно, удовлетворяет (2.3.3).
Замечание. В частности, для уравнения первого порядка формула (2.3.5) совпадает с формулой (1.1.8) при у0 = 0. В импульсной функцией (1.1.8) является множитель 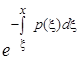 , который согласно (1.1.5), удовлетворяет одному уравнению и обращается в единицу при x = x
, который согласно (1.1.5), удовлетворяет одному уравнению и обращается в единицу при x = x



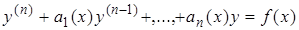 (2.3.1)
(2.3.1)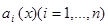 непрерывны на интервале X.
непрерывны на интервале X.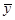 (x) - частное решение неоднородного уравнения (2.3.1), то любое решение у(x) неоднородного уравнения (2.3.1) представляется в виде
(x) - частное решение неоднородного уравнения (2.3.1), то любое решение у(x) неоднородного уравнения (2.3.1) представляется в виде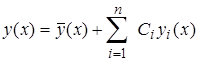 (2.3.2)
(2.3.2)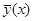 .
.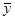 (x). Согласно теореме 2.5 эта разность удовлетворяет однородному уравнению (2.2.1), и, значит, по теореме 1.5
(x). Согласно теореме 2.5 эта разность удовлетворяет однородному уравнению (2.2.1), и, значит, по теореме 1.5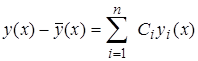
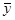 (x), удовлетворяющее начальным условиям
(x), удовлетворяющее начальным условиям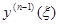
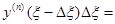

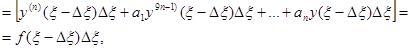
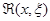 , указывая зависимость от начальной точки, и назовём его импульсной функцией), а затем умножить его на f(x)Dx. Итак,
, указывая зависимость от начальной точки, и назовём его импульсной функцией), а затем умножить его на f(x)Dx. Итак, 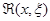 строится как решение однородного уравнения, удовлетворяющее условиям
строится как решение однородного уравнения, удовлетворяющее условиям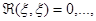
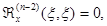
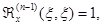 (2.3.4)
(2.3.4)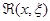 f(x)Dx. Суммируя теперь элементарные воздействия на основании того же принципа суперпозиции и перехода от суммы к интегралу, получим решение, удовлетворяющее условию (2.3.3):
f(x)Dx. Суммируя теперь элементарные воздействия на основании того же принципа суперпозиции и перехода от суммы к интегралу, получим решение, удовлетворяющее условию (2.3.3):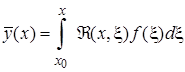 . (2.3.5)
. (2.3.5)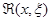 , называемая импульсной функцией, удовлетворяет однородному уравнению (2.2.1) и начальным условиям (2.3.4), является частным решением неоднородного уравнения (2.3.1), удовлетворяющим нулевым начальным условиям (2.3.3).
, называемая импульсной функцией, удовлетворяет однородному уравнению (2.2.1) и начальным условиям (2.3.4), является частным решением неоднородного уравнения (2.3.1), удовлетворяющим нулевым начальным условиям (2.3.3).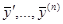 . Предварительно заметим, что так как x является параметром, принадлежащим тому же множеству, что и x, то (2.3.4) равносильно записи
. Предварительно заметим, что так как x является параметром, принадлежащим тому же множеству, что и x, то (2.3.4) равносильно записи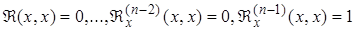
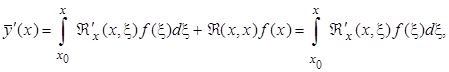
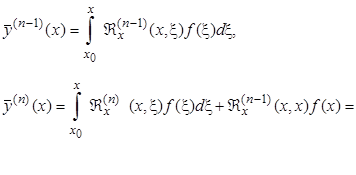
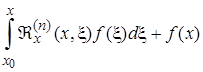
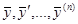 в (2.3.1), получим
в (2.3.1), получим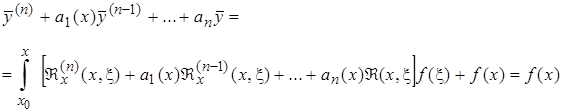
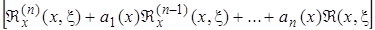 под интегралом обращается в нуль в силу определения
под интегралом обращается в нуль в силу определения 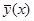 действительно является решением уравнения (2.3.1) и, кроме того, очевидно, удовлетворяет (2.3.3).
действительно является решением уравнения (2.3.1) и, кроме того, очевидно, удовлетворяет (2.3.3).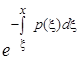 , который согласно (1.1.5), удовлетворяет одному уравнению и обращается в единицу при x = x
, который согласно (1.1.5), удовлетворяет одному уравнению и обращается в единицу при x = x

