Дифференциальные уравнения. Рассмотрим задачу Коши для линейного дифференциального уравнения
 (18.1)
(18.1)
(здесь  ) с начальными условиями
) с начальными условиями
 . (18.2)
. (18.2)
Переходя в (18.1) к изображениям, в силу линейности преобразования Лапласа будем иметь
 . (18.3)
. (18.3)
Изображения производных, используя теорему 3 § 16 и начальные условия (18.2), запишем в виде
 . (18.4)
. (18.4)
Подставив (18.4) в (18.3), после несложных преобразований получим операторное уравнение
 , (18.5)
, (18.5)
где  (характеристический многочлен);
(характеристический многочлен); 
 .
.
Из уравнения (18.5) найдем операторное решение
 . (18.6)
. (18.6)
Решением задачи Коши (18.1), (18.2) является оригинал операторного решения (18.6):

Для задачи Коши  в принятых обозначениях можно записать
в принятых обозначениях можно записать
 ;
;
 ;
;
 .
.
Операторное уравнение имеет вид
 .
.
разложим операторное решение на простейшие дроби:

 .
.
С помощью формул, полученных в § 15, получим оригиналы:
 .
.
Таким образом, решение задачи Коши будет иметь вид
 .
.
Пример 1. Решить задачу Коши для дифференциального уравнения  с начальными условиями
с начальными условиями  , где
, где  .
.
Решение. Запишем операторное уравнение
 .
.
Его решение имеет вид
 .
.
Используя теорему 2 § 16, последовательно найдем:


 .
.
Пример 2. Решить задачу Коши для дифференциального уравнения  с нулевыми начальными условиями, где
с нулевыми начальными условиями, где  – ступенчатая импульсная функция.
– ступенчатая импульсная функция.
Решение. Запишем операторное уравнение

и его решение
 .
.
Из теоремы 2 § 16 следует
 ;
;
в соответствии с теоремой запаздывания (§ 15)
 .
.
Окончательно,
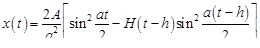 .
.
Пример 3. На точку массой т, прикрепленную к пружине жесткостью с и находящуюся на гладкой горизонтальной плоскости, действует периодически меняющаяся сила 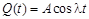 . В момент времени t точка подверглась удару, несущему импульс
. В момент времени t точка подверглась удару, несущему импульс  . Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.
. Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.
Решение. Уравнение движения запишем в виде
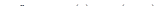 ,
,
где  – упругая сила;
– упругая сила; 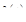 – функция Дирака. Решим операторное уравнение
– функция Дирака. Решим операторное уравнение
 ,
,
где  . При
. При 

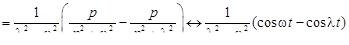 .
.
Если  (случай резонанса), то
(случай резонанса), то
 .
.
По теореме запаздывания
 .
.
Окончательно,

Интеграл (формула) Дюамеля. Рассмотрим задачу Коши для уравнения (18.1) при начальных условиях 
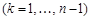 . Операторное решение в этом случае имеет вид
. Операторное решение в этом случае имеет вид
 .
.
Пусть весовая функция  – оригинал для
– оригинал для  . тогда по теореме 1 § 16 получим
. тогда по теореме 1 § 16 получим
 . (18.7)
. (18.7)
Соотношение (18.7) называется интегралом (формулой) Дюамеля.
Замечание. При ненулевых начальных условиях формула Дюамеля непосредственно неприменима. В этом случае необходимо предварительно преобразовать исходную задачу к задаче с однородными (нулевыми) начальными условиями. Для этого введем новую функцию  , полагая
, полагая
 (18.8)
(18.8)
где  – начальные значения искомого решения
– начальные значения искомого решения  .
.
Как легко видеть,  , и следовательно,
, и следовательно,  .
.
Таким образом, функция  – решение уравнения (18.1) с правой частью
– решение уравнения (18.1) с правой частью 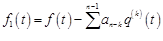 , полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.
, полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.
Используя (18.7), найдем  и
и 
 .
.
Пример 4. С помощью интеграла Дюамеля найти решение задачи Коши

с начальными условиями  .
.
Решение. Начальные данные ненулевые. Полагаем, в соответствии с (18.8),  . Тогда
. Тогда 
 , и для определения
, и для определения  получим уравнение
получим уравнение  с однородными начальными условиями.
с однородными начальными условиями.
Для рассматриваемой задачи характеристический многочлен  , весовая функция
, весовая функция  . По формуле Дюамеля
. По формуле Дюамеля

 .
.
Окончательно,
 .
.
Системы линейных дифференциальных уравнений с постоянными коэффициентами. Задача Коши для системы линейных дифференциальных уравнений в матричной записи имеет вид
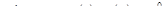 , (18.9)
, (18.9)
где  – вектор искомых функций;
– вектор искомых функций;  – вектор правых частей;
– вектор правых частей;  – матрица коэффициентов;
– матрица коэффициентов;  – вектор начальных данных.
– вектор начальных данных.
Переходя в (18.9) к изображениям, получим операторную систему
 , (18.10)
, (18.10)
где  – Лаплас-образы векторов искомых функций и правых частей соответственно.
– Лаплас-образы векторов искомых функций и правых частей соответственно.
Из (18.10) находим операторное решение
 , (18.11)
, (18.11)
где  ; Е – единичная матрица.
; Е – единичная матрица.
Оригинал  операторного решения
операторного решения  (18.11) является решением исходной задачи Коши (18.9).
(18.11) является решением исходной задачи Коши (18.9).
Обозначим  весовую матрицу, т.е. матрицу-оригинал для
весовую матрицу, т.е. матрицу-оригинал для 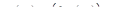 , где
, где 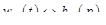 Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь
Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь
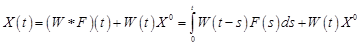 . (18.12)
. (18.12)
При нулевых начальных условиях
 . (18.13)
. (18.13)
Соотношение (18.13) представляет собой матричный аналог интеграла Дюамеля.
Пример 5. Найти решение задачи Коши

с начальными условиями  .
.
Решение. Запишем систему и начальные условия в матричной форме:
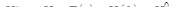 ,
,
где  . Тогда
. Тогда

 ;
;


 .
.
Окончательно, по формуле (18.12) получим

или

Замечание. Формулы (18.12) и (18.13) имеют большое теоретическое значение, поскольку позволяют исследовать поведение решения системы дифференциальных уравнений в зависимости от начальных данных и правых частей. Однако для практического применения эти формулы мало пригодны, так как зачастую требуют проведения громоздких выкладок, связанных с вычислением обратных матриц, матричных сверток и т.п. Поэтому на практике обычно применяют операторный метод, не переходя к матричной записи системы уравнений, а при решении операторной системы используют конкретные особенности исследуемой задачи.
Пример 6. Решить задачу Коши:

с начальными условиями  .
.
Решение. Перейдем в данной системе к изображениям. С учетом начальных условий будем иметь
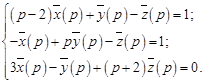
Запишем решение операторной системы
 .
.
Тогда
 .
.
Приложения
Электрические цепи. Основными элементами электрических цепей являются сопротивления, индуктивности и емкости (конденсаторы). Каждый из этих элементов называются двухполюсником, поскольку он обладает двумя контактами (полюсами), которые соединяются с полюсами других элементов цепи. Электрическое состояние двухполюсника в каждый момент времени 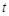 определяется двумя величинами: силой тока (током)
определяется двумя величинами: силой тока (током)  , проходящего через двухполюсник, и падением напряжения (напряжением)
, проходящего через двухполюсник, и падением напряжения (напряжением)  на его полюсах. Для каждого двухполюсника функции
на его полюсах. Для каждого двухполюсника функции 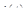 и
и  связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
Для сопротивления имеет место закон Ома
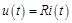 ,
,
где 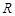 – сопротивление двухполюсника.
– сопротивление двухполюсника.
Для индуктивности справедливо соотношение
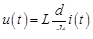 ,
,
где  – индуктивность двухполюсника.
– индуктивность двухполюсника.
Для конденсатора выполняется соотношение
 ,
,
где С – емкость конденсатора;  – начальный заряд на его обкладках.
– начальный заряд на его обкладках.
В дальнейшем будем считать, что в начальный момент времени  цепь была свободна от токов и зарядов, что соответствует задачам включения.
цепь была свободна от токов и зарядов, что соответствует задачам включения.
Если ввести операторный ток  и операторное напряжение
и операторное напряжение  как изображения функций
как изображения функций  и
и  соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
 .
.
Последние соотношения могут быть записаны в виде операторного закона Ома
 ,
,
где операторное сопротивление (импеданс)  в случае активного сопротивления, индуктивности и емкости принято в виде соответственно
в случае активного сопротивления, индуктивности и емкости принято в виде соответственно  . Величину, обратную
. Величину, обратную  ,
,  называют операторной проводимостью (адмитансом) двухполюсника.
называют операторной проводимостью (адмитансом) двухполюсника.
При последовательном соединении двух двухполюсников с операторными сопротивлениями 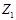 и
и  имеем
имеем  ;
; 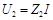 и
и  , откуда
, откуда  , и следовательно, импеданс цепи
, и следовательно, импеданс цепи  . Аналогично, при параллельном соединении двух элементов с адмитансами
. Аналогично, при параллельном соединении двух элементов с адмитансами  и
и  получим
получим 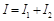 ,
,  ,
,  , откуда
, откуда  , и следовательно, адмитанс цепи
, и следовательно, адмитанс цепи  .
.
Таким образом, в задачах включения операторные сопротивления и проводимости цепей рассчитываются по обычным правилам соединения активных сопротивлений. Например, если цепь состоит из последовательно соединенных сопротивления  , индуктивности
, индуктивности  и емкости
и емкости 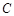 , шунтированной сопротивлением
, шунтированной сопротивлением  , то ее импеданс
, то ее импеданс  .
.
Если электрическая цепь с адмитансом  включена на эдс
включена на эдс 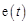 , то операторный ток в ней определяется соотношением
, то операторный ток в ней определяется соотношением  ,
,  .
.
Как правило, операторная проводимость цепи  представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости
представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости  , что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
, что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
Если эдс 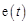 является ограниченной функцией времени, то полюсы функции
является ограниченной функцией времени, то полюсы функции  имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
 ,
,
где  ;
;  – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями;
с положительными мнимыми частями;  – мнимая единица. Здесь, как и ранее, предполагаем, что функция
– мнимая единица. Здесь, как и ранее, предполагаем, что функция  не имеет кратных полюсов.
не имеет кратных полюсов.
Представим эдс тригонометрическим рядом Фурье  . Тогда
. Тогда
 ;
;
 ;
;  ,
,
следовательно,
 .
.
Положим
 ,
,
где 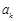 – амплитуда гармоники с частотой
– амплитуда гармоники с частотой 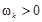 , b k – ее начальная фаза;
, b k – ее начальная фаза;
 ; g
; g  . Тогда
. Тогда
 . (19.1)
. (19.1)
Функции  и
и 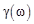 называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы.
называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы.
Будем трактовать функции 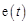 и
и  , как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой
, как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой  и с фазой, сдвинутой относительно фазы входного сигнала на величину
и с фазой, сдвинутой относительно фазы входного сигнала на величину  . Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ
. Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ  достигает максимума, называется резонансной частотой системы.
достигает максимума, называется резонансной частотой системы.
Пример. Колебательный контур состоит из последовательно соединенных активного сопротивления  , индуктивности
, индуктивности  и емкости C. Найти резонансную частоту.
и емкости C. Найти резонансную частоту.
Решение. Импеданс контура  , его адмитанс
, его адмитанс  . Амплитудно-частотная и фазочастотная характеристики соответственно
. Амплитудно-частотная и фазочастотная характеристики соответственно

 ;
;
 . (19.2)
. (19.2)
Из формулы (19.2) следует, что АЧХ достигает наибольшего значения, если  .
.
Таким образом, колебательный контур резонирует на частоту  , наибольший коэффициент усиления сигнала равен
, наибольший коэффициент усиления сигнала равен  , сдвиг фазы на резонансной частоте равен нулю.
, сдвиг фазы на резонансной частоте равен нулю.
Расчет длинных электрических линий. Обозначим  – удельные сопротивление, индуктивность и емкость провода соответственно;
– удельные сопротивление, индуктивность и емкость провода соответственно;  – коэффициент утечки тока;
– коэффициент утечки тока;  и
и  – ток и напряжение в точке с координатой х в момент времени
– ток и напряжение в точке с координатой х в момент времени  . Тогда для участка линии между точками х и
. Тогда для участка линии между точками х и 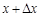 по известным законам физики будем иметь
по известным законам физики будем иметь
 ;
;
 . (19.3)
. (19.3)
Разделив уравнения (19.3) на D х и перейдя к пределу при D х ® 0, получим систему уравнений в частных производных (телеграфную систему) для определения функций  и
и  :
:
 ;
;
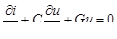 . (19.4)
. (19.4)
Для завершения постановки задачи систему (19.4) необходимо дополнить начальными и краевыми условиями. В задаче включения начальные условия имеют вид
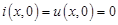 . (19.5)
. (19.5)
Далее примем, что правый конец провода заземлен, а на левом его конце поддерживается заданное напряжение  . Тогда краевые условия запишутся в виде
. Тогда краевые условия запишутся в виде
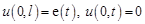 , (19.6)
, (19.6)
где  – длина линии.
– длина линии.
Применяя к системе (19.4) преобразование Лапласа по переменной 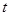 с учетом начальных условий (19.5), получим операторную систему
с учетом начальных условий (19.5), получим операторную систему
 , (19.7)
, (19.7)
где  и
и 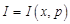 – изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в
– изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в
 , (19.8)
, (19.8)
где  .
.
Применяя снова преобразование Лапласа, на этот раз по переменной х, вместо (19.7) запишем алгебраическую систему
 ;
;  , (19.9)
, (19.9)
где  ;
;  ;
;  ;
;  – параметр преобразования Лапласа по переменной х.
– параметр преобразования Лапласа по переменной х.
В дальнейшем, чтобы избежать громоздких выкладок, ограничимся исследованием установившегося режима в линии без искажений, т.е. линии, параметры которой удовлетворяют условию  .
.
Решение системы (19.9) для линии без искажений имеет вид
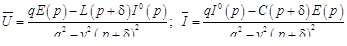 ,
,
где  .
.
Возвратимся к оригиналам:
 ;
;
 . (19.10)
. (19.10)
С помощью второго из краевых условий (19.8) найдем
 . (19.11)
. (19.11)
Из (19.10) и (19.11) следует, что
 ;
;
 . (19.12)
. (19.12)
При отыскании функций  и
и  будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения
будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения  , откуда
, откуда  и
и  ,
, 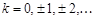 Следовательно, нули функции
Следовательно, нули функции 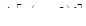 – это числа
– это числа 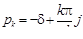 , расположенные в левой полуплоскости
, расположенные в левой полуплоскости 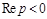 . Поэтому, если
. Поэтому, если 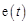 – ограниченная функция, то, как следует из (19.12), напряжение и ток в установившемся режиме соответственно
– ограниченная функция, то, как следует из (19.12), напряжение и ток в установившемся режиме соответственно


где  – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями.
с положительными мнимыми частями.
В частности, если 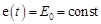 , то
, то  , и следовательно, в установившемся режиме
, и следовательно, в установившемся режиме
 ;
;
 .
.
Примеры для самостоятельного решения
Задание 1. Разложить в ряд Фурье функции, заданные на интервале [–p, p]:
1. 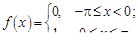
 2.
2. 
3.  . 4.
. 4. 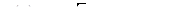 .
.
5.  6.
6. 
7.  8.
8. 
9. 
10. 
11.  12.
12. 
13.  14.
14. 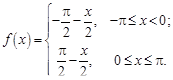
15.  16.
16. 
17.  18.
18. 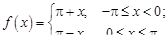
19.  20.
20. 
21. 
22. 
23. 
24. 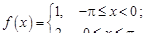
25.  26.
26. 
27. 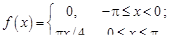 28.
28. 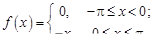
29.  30.
30. 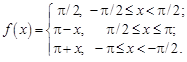
31. 
Задание 2. Разложить в ряд Фурье функции, заданные на интервале  :
:
1.  2.
2. 
3.  4.
4. 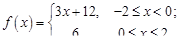
5.  6.
6. 
7.  8.
8. 
9. 
10. 
11. 
12. 
13.  14.
14. 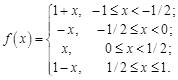
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 
25. 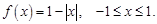 26.
26. 
27. 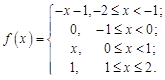 28.
28. 
29 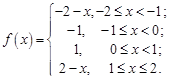 30.
30.  =
= 
Указание. Для решения примера 15 воспользоваться формулами [6]

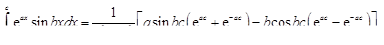
Задание 3. Представить интегралом Фурье следующие функции:
1. 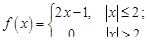 2.
2. 
3.  4.
4. 
5.  6.
6. 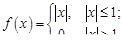
7.  8.
8. 
9. 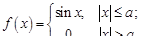 10.
10. 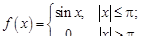
11. 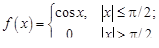 12.
12. 
13.  . 14.
. 14. 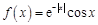 . 15.
. 15.  .
.
16.  . 17.
. 17.  . 18.
. 18.  .
.
Указание. При решении следует воспользоваться формулами
 ;
;
 ;
;

 ;
;

 ;
;
 ;
; 
 .
.
Задание 4. Найти косинус-преобразование Фурье  следующих функций:
следующих функций:
1.  2.
2.  . 3.
. 3.  .
.
4.  . 5.
. 5.  .
.
Задание 5. Найти синус-преобразование Фурье  следующих функций:
следующих функций:
1.  2.
2. 
3.  4.
4. 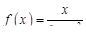 .
.
5.  . 6.
. 6.  . 7.
. 7.  .
.
Ответы
Задание 1
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  .
.
8.  .
.
9. 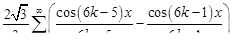 .
.
10.  .
.
11.  .
.
12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  .
.
20. 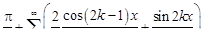 .
.
21.  .
.
22.  .
.
23. 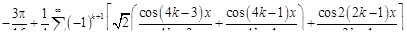 .
.
24.  . 25.
. 25.  .
.
26.  .
.
27.  .
.
28.  .
.
29. 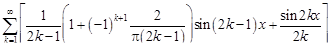 .
.
30.  .
.
31. 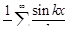 .
.
Задание 2
 .
.
2.  .
.
3.  .
.
4.  .
.
5.  . 6.
. 6.  . 7.
. 7. 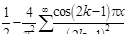 .
.
8. 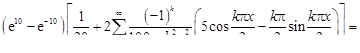
 .
.
9.  .
.
10. 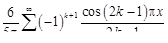 . 11.
. 11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  . 17.
. 17. 
18.  . 19.
. 19.  .
.
20.  .
.
21.  .
.
22.  . 23.
. 23.  .
.
24.  . 25.
. 25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
Задание 3
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  . 7.
. 7.  .
.
8.  . 9.
. 9.  . 10.
. 10.  .
.
11. ![]() ((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228268']=__lxGc__['s']['_228268']||{'b':{}})['b']['_697691']={'i':__lxGc__.b++};
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228268']=__lxGc__['s']['_228268']||{'b':{}})['b']['_697691']={'i':__lxGc__.b++};



 (18.1)
(18.1) ) с начальными условиями
) с начальными условиями . (18.2)
. (18.2) . (18.3)
. (18.3) . (18.4)
. (18.4) , (18.5)
, (18.5) (характеристический многочлен);
(характеристический многочлен); 
 .
. . (18.6)
. (18.6)
 в принятых обозначениях можно записать
в принятых обозначениях можно записать ;
; ;
; .
. .
.
 .
. .
. .
. с начальными условиями
с начальными условиями  , где
, где  .
. .
. .
.

 .
. с нулевыми начальными условиями, где
с нулевыми начальными условиями, где  – ступенчатая импульсная функция.
– ступенчатая импульсная функция.
 .
. ;
; .
.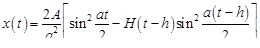 .
.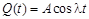 . В момент времени t точка подверглась удару, несущему импульс
. В момент времени t точка подверглась удару, несущему импульс  . Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.
. Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат. ,
, – упругая сила;
– упругая сила;  – функция Дирака. Решим операторное уравнение
– функция Дирака. Решим операторное уравнение ,
, . При
. При 

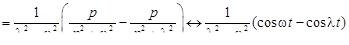 .
. (случай резонанса), то
(случай резонанса), то .
. .
.

 . Операторное решение в этом случае имеет вид
. Операторное решение в этом случае имеет вид .
. – оригинал для
– оригинал для  . тогда по теореме 1 § 16 получим
. тогда по теореме 1 § 16 получим . (18.7)
. (18.7) , полагая
, полагая (18.8)
(18.8) – начальные значения искомого решения
– начальные значения искомого решения  .
. , и следовательно,
, и следовательно,  .
.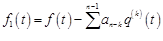 , полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.
, полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных. и
и 
 .
.
 .
. . Тогда
. Тогда 
 , и для определения
, и для определения  получим уравнение
получим уравнение  с однородными начальными условиями.
с однородными начальными условиями. , весовая функция
, весовая функция  . По формуле Дюамеля
. По формуле Дюамеля
 .
. .
.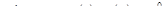 , (18.9)
, (18.9) – вектор искомых функций;
– вектор искомых функций;  – вектор правых частей;
– вектор правых частей;  – матрица коэффициентов;
– матрица коэффициентов;  – вектор начальных данных.
– вектор начальных данных. , (18.10)
, (18.10) – Лаплас-образы векторов искомых функций и правых частей соответственно.
– Лаплас-образы векторов искомых функций и правых частей соответственно. , (18.11)
, (18.11) ; Е – единичная матрица.
; Е – единичная матрица. операторного решения
операторного решения  (18.11) является решением исходной задачи Коши (18.9).
(18.11) является решением исходной задачи Коши (18.9). весовую матрицу, т.е. матрицу-оригинал для
весовую матрицу, т.е. матрицу-оригинал для 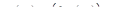 , где
, где 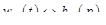 Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь
Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь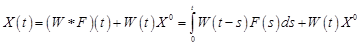 . (18.12)
. (18.12) . (18.13)
. (18.13)
 .
.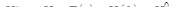 ,
, . Тогда
. Тогда
 ;
;

 .
.


 .
.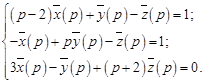
 .
. .
. определяется двумя величинами: силой тока (током)
определяется двумя величинами: силой тока (током)  , проходящего через двухполюсник, и падением напряжения (напряжением)
, проходящего через двухполюсник, и падением напряжения (напряжением)  на его полюсах. Для каждого двухполюсника функции
на его полюсах. Для каждого двухполюсника функции  и
и  связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.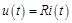 ,
, – сопротивление двухполюсника.
– сопротивление двухполюсника.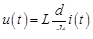 ,
, – индуктивность двухполюсника.
– индуктивность двухполюсника. ,
, – начальный заряд на его обкладках.
– начальный заряд на его обкладках. цепь была свободна от токов и зарядов, что соответствует задачам включения.
цепь была свободна от токов и зарядов, что соответствует задачам включения. и операторное напряжение
и операторное напряжение  как изображения функций
как изображения функций  и
и  соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие: .
. ,
, . Величину, обратную
. Величину, обратную  ,
,  называют операторной проводимостью (адмитансом) двухполюсника.
называют операторной проводимостью (адмитансом) двухполюсника.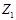 и
и  имеем
имеем  ;
; 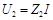 и
и  , откуда
, откуда  , и следовательно, импеданс цепи
, и следовательно, импеданс цепи  . Аналогично, при параллельном соединении двух элементов с адмитансами
. Аналогично, при параллельном соединении двух элементов с адмитансами  и
и  получим
получим 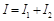 ,
,  ,
,  , откуда
, откуда  , и следовательно, адмитанс цепи
, и следовательно, адмитанс цепи  .
. , индуктивности
, индуктивности  и емкости
и емкости 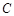 , шунтированной сопротивлением
, шунтированной сопротивлением  , то ее импеданс
, то ее импеданс  .
.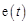 , то операторный ток в ней определяется соотношением
, то операторный ток в ней определяется соотношением  ,
,  .
. представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости
представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости  , что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
, что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний. ,
, ;
;  – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями;
с положительными мнимыми частями;  – мнимая единица. Здесь, как и ранее, предполагаем, что функция
– мнимая единица. Здесь, как и ранее, предполагаем, что функция  . Тогда
. Тогда ;
; ;
;  ,
, .
. ,
,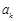 – амплитуда гармоники с частотой
– амплитуда гармоники с частотой 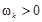 , b k – ее начальная фаза;
, b k – ее начальная фаза; ; g
; g  . Тогда
. Тогда . (19.1)
. (19.1) и
и 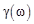 называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы.
называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы. , как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой
, как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой  и с фазой, сдвинутой относительно фазы входного сигнала на величину
и с фазой, сдвинутой относительно фазы входного сигнала на величину  . Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ
. Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ  достигает максимума, называется резонансной частотой системы.
достигает максимума, называется резонансной частотой системы. , его адмитанс
, его адмитанс  . Амплитудно-частотная и фазочастотная характеристики соответственно
. Амплитудно-частотная и фазочастотная характеристики соответственно
 ;
; . (19.2)
. (19.2) .
. , наибольший коэффициент усиления сигнала равен
, наибольший коэффициент усиления сигнала равен  , сдвиг фазы на резонансной частоте равен нулю.
, сдвиг фазы на резонансной частоте равен нулю. – удельные сопротивление, индуктивность и емкость провода соответственно;
– удельные сопротивление, индуктивность и емкость провода соответственно;  – коэффициент утечки тока;
– коэффициент утечки тока;  и
и  – ток и напряжение в точке с координатой х в момент времени
– ток и напряжение в точке с координатой х в момент времени  . Тогда для участка линии между точками х и
. Тогда для участка линии между точками х и 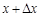 по известным законам физики будем иметь
по известным законам физики будем иметь ;
; . (19.3)
. (19.3) и
и  :
: ;
;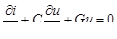 . (19.4)
. (19.4)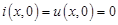 . (19.5)
. (19.5) . Тогда краевые условия запишутся в виде
. Тогда краевые условия запишутся в виде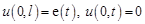 , (19.6)
, (19.6) – длина линии.
– длина линии.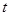 с учетом начальных условий (19.5), получим операторную систему
с учетом начальных условий (19.5), получим операторную систему , (19.7)
, (19.7) и
и 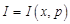 – изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в
– изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в , (19.8)
, (19.8) .
. ;
;  , (19.9)
, (19.9) ;
;  ;
;  ;
;  – параметр преобразования Лапласа по переменной х.
– параметр преобразования Лапласа по переменной х. .
.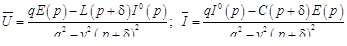 ,
, .
. ;
; . (19.10)
. (19.10) . (19.11)
. (19.11) ;
; . (19.12)
. (19.12) и
и  будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения
будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения  , откуда
, откуда  и
и  ,
, 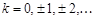 Следовательно, нули функции
Следовательно, нули функции 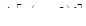 – это числа
– это числа 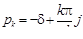 , расположенные в левой полуплоскости
, расположенные в левой полуплоскости 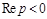 . Поэтому, если
. Поэтому, если 

 – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями.
с положительными мнимыми частями. , то
, то  , и следовательно, в установившемся режиме
, и следовательно, в установившемся режиме ;
; .
.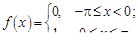
 2.
2. 
 . 4.
. 4. 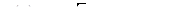 .
. 6.
6. 
 8.
8. 


 12.
12. 
 14.
14. 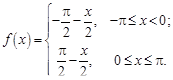
 16.
16. 
 18.
18. 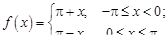
 20.
20. 



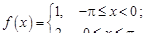
 26.
26. 
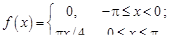 28.
28. 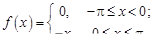
 30.
30. 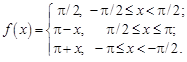

 :
: 2.
2. 
 4.
4. 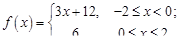
 6.
6. 
 8.
8. 




 14.
14. 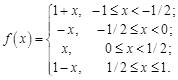
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
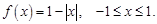 26.
26. 
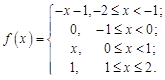 28.
28. 
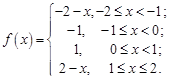 30.
30.  =
= 

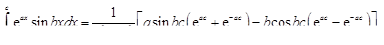
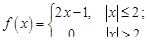 2.
2. 
 4.
4. 
 6.
6. 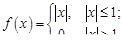
 8.
8. 
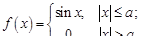 10.
10. 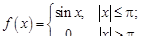
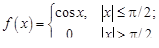 12.
12. 
 . 14.
. 14. 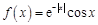 . 15.
. 15.  .
. . 17.
. 17.  . 18.
. 18.  .
. ;
; ;
;
 ;
;
 ;
;  .
. следующих функций:
следующих функций: 2.
2.  . 3.
. 3.  .
. . 5.
. 5.  .
. следующих функций:
следующих функций:
 4.
4. 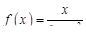 .
. . 6.
. 6.  . 7.
. 7.  .
. . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. .
. .
.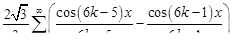 .
. .
. .
. .
. . 14.
. 14.  .
. . 16.
. 16.  .
. . 18.
. 18.  .
. .
.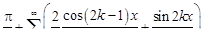 .
. .
. .
.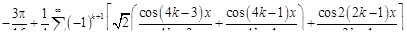 .
. . 25.
. 25.  .
. .
. .
. .
.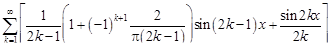 .
. .
.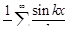 .
. .
. .
. .
. .
. . 6.
. 6.  . 7.
. 7. 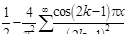 .
.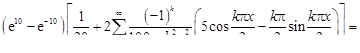
 .
. .
.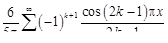 . 11.
. 11.  .
. .
. .
. .
. .
. . 17.
. 17. 
 . 19.
. 19.  .
. .
. .
. . 23.
. 23.  .
. . 25.
. 25.  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. . 7.
. 7.  .
. . 9.
. 9.  . 10.
. 10.  .
.


