§ 14. Преобразование Лапласа
Понятие оригинала. Кусочно-непрерывная функция  называется оригиналом, если выполняются следующие условия:
называется оригиналом, если выполняются следующие условия:
1) 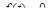 для всех отрицательных t;
для всех отрицательных t;
2) при 
 растет не быстрее экспоненты, т.е. существуют такие постоянные M > 0 и c > 0, что
растет не быстрее экспоненты, т.е. существуют такие постоянные M > 0 и c > 0, что  для всех t.
для всех t.
Число с называется показателем роста 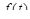 . очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
. очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
Простейшим оригиналом является единичная функция Хевисайда

Если функция  удовлетворяет условию 2 и не удовлетворяет 1, то произведение
удовлетворяет условию 2 и не удовлетворяет 1, то произведение  будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
Легко видеть, что оригиналами являются такие функции, как  и т.п.
и т.п.
Можно доказать, что сумма, разность и произведение оригиналов являются оригиналами и что оригиналом является функция  при
при 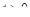 (доказательства следует найти самостоятельно).
(доказательства следует найти самостоятельно).
Замечание. Из этих утверждений следует, что многочлены произвольной степени 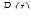 , а также функции вида
, а также функции вида  являются оригиналами.
являются оригиналами.
Интеграл Лапласа. Интегралом Лапласа для оригинала f (t) называется несобственный интеграл вида
 , (14.1)
, (14.1)
где  – комплексный параметр.
– комплексный параметр.
Теорема. Интеграл Лапласа абсолютно сходится в полуплоскости П с: 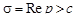 , где с – показатель роста f (t). В самом деле, по определению оригинала имеем
, где с – показатель роста f (t). В самом деле, по определению оригинала имеем  . Таким образом, интеграл (14.1) мажорируется сходящимся интегралом
. Таким образом, интеграл (14.1) мажорируется сходящимся интегралом 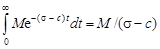 , и, следовательно, сходится абсолютно в П с.
, и, следовательно, сходится абсолютно в П с.
Замечание. При доказательстве теоремы получено используемое в дальнейшем неравенство:
 (14.2)
(14.2)
Преобразование Лапласа. Интеграл Лапласа
 (14.3)
(14.3)
представляет собой функцию параметра p, определенную в полуплоскости П с:  . Функция
. Функция  называется Лаплас-образом (изображением по Лапласу) оригинала
называется Лаплас-образом (изображением по Лапласу) оригинала  . Тот факт, что
. Тот факт, что  есть Лаплас-образ
есть Лаплас-образ  , обозначается
, обозначается  или
или  .
.
Соотношение (14.3), устанавливающее связь между оригиналом и его Лаплас-образом, называется преобразованием Лапласа.
Свойства преобразования Лапласа следующие:
1. Теорема линейности. При любых постоянных  и
и 
 .
.
Это утверждение вытекает из определения (14.3) и свойств интегралов.
2. Имеет место  , что непосредственно следует из неравенства (14.2).
, что непосредственно следует из неравенства (14.2).
3. Теорема подобия. Для любого 
 .
.
Действительно, полагая  , получим
, получим
 .
.
4. теорема смещения. Для любого а  . Действительно,
. Действительно,
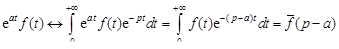 .
.
5. теорема запаздывания. Для любого 

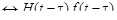 . По определению преобразования Лапласа имеем
. По определению преобразования Лапласа имеем
 .
.
Здесь учтено, что  при
при 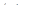 . Выполнив в последнем интеграле замену
. Выполнив в последнем интеграле замену  , получим
, получим
 .
.
Обратное преобразование Лапласа. Установим связь между преобразованиями Лапласа и Фурье. Так как при  оригинал
оригинал  , то
, то


где 
 – показатель роста
– показатель роста 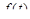 .
.
Интеграл в правой части последней формулы есть интеграл Фурье для  . Таким образом, Лаплас-образ функции
. Таким образом, Лаплас-образ функции 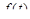 является Фурье-образом функции
является Фурье-образом функции  . Из формулы обратного преобразования Фурье получим, что в точках непрерывности
. Из формулы обратного преобразования Фурье получим, что в точках непрерывности 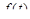
 .
.
Отсюда
 (14.4)
(14.4)
Если в точке t функция 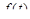 терпит разрыв, то значение интеграла в (14.4) равно полусумме односторонних пределов
терпит разрыв, то значение интеграла в (14.4) равно полусумме односторонних пределов  в этой точке.
в этой точке.
Формула (14.4) определяет обратное преобразование Лапласа, с помощью которого оригинал однозначно восстанавливается по своему изображению с точностью до значений в точках разрыва.



 называется оригиналом, если выполняются следующие условия:
называется оригиналом, если выполняются следующие условия: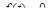 для всех отрицательных t;
для всех отрицательных t;
 для всех t.
для всех t.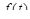 . очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
. очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
 будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t. и т.п.
и т.п. при
при 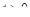 (доказательства следует найти самостоятельно).
(доказательства следует найти самостоятельно).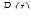 , а также функции вида
, а также функции вида  являются оригиналами.
являются оригиналами. , (14.1)
, (14.1) – комплексный параметр.
– комплексный параметр.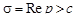 , где с – показатель роста f (t). В самом деле, по определению оригинала имеем
, где с – показатель роста f (t). В самом деле, по определению оригинала имеем  . Таким образом, интеграл (14.1) мажорируется сходящимся интегралом
. Таким образом, интеграл (14.1) мажорируется сходящимся интегралом 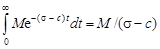 , и, следовательно, сходится абсолютно в П с.
, и, следовательно, сходится абсолютно в П с. (14.2)
(14.2) (14.3)
(14.3) . Функция
. Функция  называется Лаплас-образом (изображением по Лапласу) оригинала
называется Лаплас-образом (изображением по Лапласу) оригинала  . Тот факт, что
. Тот факт, что  есть Лаплас-образ
есть Лаплас-образ  , обозначается
, обозначается  или
или  .
. и
и 
 .
. , что непосредственно следует из неравенства (14.2).
, что непосредственно следует из неравенства (14.2).
 .
. , получим
, получим .
. . Действительно,
. Действительно,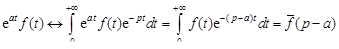 .
.

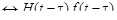 . По определению преобразования Лапласа имеем
. По определению преобразования Лапласа имеем .
. при
при 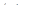 . Выполнив в последнем интеграле замену
. Выполнив в последнем интеграле замену  , получим
, получим .
. оригинал
оригинал  , то
, то


 – показатель роста
– показатель роста 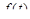 .
. . Таким образом, Лаплас-образ функции
. Таким образом, Лаплас-образ функции  .
. (14.4)
(14.4) в этой точке.
в этой точке.


