Пусть функция  имеет производную в точке а, т.е.
имеет производную в точке а, т.е. 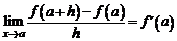 или
или 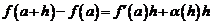 , или
, или
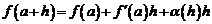 , (1)
, (1)
где 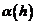 – бесконечно малая функция при
– бесконечно малая функция при 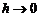 . Поскольку
. Поскольку 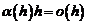 при
при 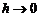 , то формулу (1) можно записать в виде
, то формулу (1) можно записать в виде
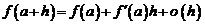 . (2)
. (2)
При 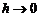 величина
величина 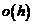 быстрее стремится к нулю, чем h. Если этой величиной пренебречь, то получим следующую приближенную формулу:
быстрее стремится к нулю, чем h. Если этой величиной пренебречь, то получим следующую приближенную формулу:
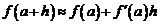 . (3)
. (3)
В общем случае сформулируем задачу так: найти многочлен n- ой степени 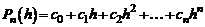 такой, чтобы имело место равенство
такой, чтобы имело место равенство
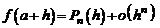 .
.
Если эту задачу решить, то всякую функцию можно заменить многочленом  . Многочлен удобен при исследовании функции. Погрешность такой замены будет мала по сравнению с
. Многочлен удобен при исследовании функции. Погрешность такой замены будет мала по сравнению с 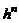 .
.
Предположим, что функция  имеет в некоторой окрестности точки а производные до порядка n включительно. В этом случае имеет место следующее соотношение:
имеет в некоторой окрестности точки а производные до порядка n включительно. В этом случае имеет место следующее соотношение:
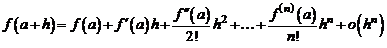 . (4)
. (4)
Эта формула носит название формулы Тейлора.
Величину 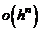 называют остаточным членом формулы Тейлора в форме Пеано. Имеют место и другие выражения для остаточного члена. В частности, если предположить существование
называют остаточным членом формулы Тейлора в форме Пеано. Имеют место и другие выражения для остаточного члена. В частности, если предположить существование 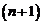 -ой производной в некоторой окрестности точки а, то справедливо равенство
-ой производной в некоторой окрестности точки а, то справедливо равенство
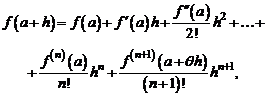 (6)
(6)
где 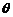 – некоторое число,
– некоторое число, 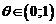 .
.
Формула (6) называется формулой Тейлора с остаточным членом в форме Лагранжа.
Если положить 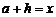 , то формула (4) будет иметь вид
, то формула (4) будет иметь вид
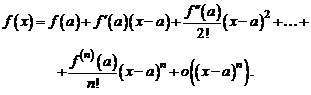 (7)
(7)
Если здесь положить 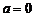 , то получим формулу Маклорена:
, то получим формулу Маклорена:
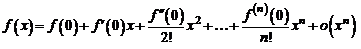 . (8)
. (8)
Если в формуле (7) перенести в левую часть 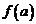 и обозначить
и обозначить 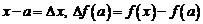 , то будем иметь
, то будем иметь
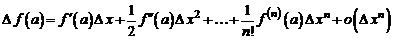 .
.
Заменяя здесь 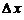 на
на 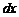 и принимая во внимание формулы (3.1), (3.2), получим
и принимая во внимание формулы (3.1), (3.2), получим
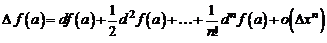 . (9)
. (9)
Таким образом, предполагая, что 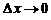 , по приведенной формуле (9) из бесконечно малого приращения
, по приведенной формуле (9) из бесконечно малого приращения 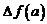 можно выделить не только его главный член – первый дифференциал, но и члены более высокого порядка малости, совпадающие с точностью до факториалов в знаменателях с последовательными дифференциалами
можно выделить не только его главный член – первый дифференциал, но и члены более высокого порядка малости, совпадающие с точностью до факториалов в знаменателях с последовательными дифференциалами 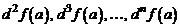 .
.
Разложение элементарных функций
по формуле Тейлора
Полагая в формуле (6.6) 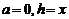 получим формулу Маклорена
получим формулу Маклорена
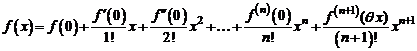 , (1)
, (1)
с остаточным членом в форме Лагранжа 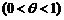 .
.
10. Разложение функции 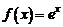 . Имеем
. Имеем
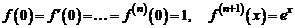 .
.
Формула Тейлора (Маклорена) с остаточным членом в форме Лагранжа принимает вид
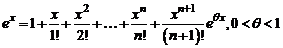 . (2)
. (2)
При любом фиксированном x остаточный член в ней стремится к нулю, так как 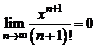 .
.
20. Разложение функции 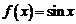 . Имеем
. Имеем
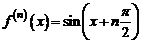 ,
, 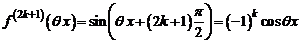 .
.
Формула (1) в данном случае принимает вид
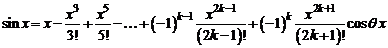 , (3)
, (3)
где при любом фиксированном x остаточный член 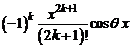 стремится к нулю при
стремится к нулю при 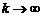 .
.
30. Разложение функции 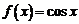 . Поскольку
. Поскольку
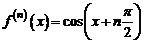 ,
, 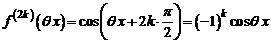 ,
,
то
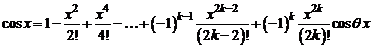 . (4)
. (4)
И в этом случае остаточный член стремится к нулю при 
40. Разложение функции 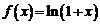 . Имеем
. Имеем
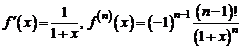 .
.
Следовательно,
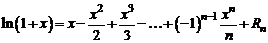 ,
,
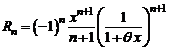 .
.
Заметим, что если 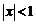 , то
, то 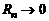 при
при 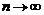 .
.
50. Разложение функции 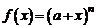 , где а – действительное число, n – натуральное число.
, где а – действительное число, n – натуральное число.
Поскольку k- ая производная данной функции
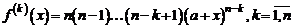 ,
,
то при 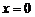 получаем
получаем
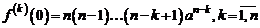 .
.
Значит,
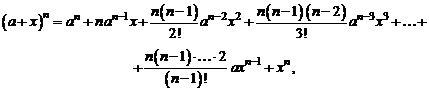
т. е. получаем разложение по биному Ньютона.
Приложения формулы Тейлора
Если в формуле (7.1) отбросить остаточный член, то получим приближенную формулу
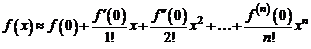 , (1)
, (1)
которая заменяет функцию 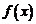 многочленом n- ой степени.
многочленом n- ой степени.
Качество этой формулы оценивается границами погрешности для остаточного члена 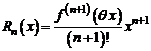 , либо порядком малости этой погрешности
, либо порядком малости этой погрешности 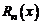 при
при 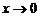 , т. е. она записывается в виде
, т. е. она записывается в виде 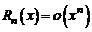 .
.
Например, если 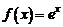 , то получаем приближенную формулу
, то получаем приближенную формулу
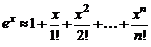 . (2)
. (2)
Так как в данном случае 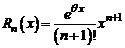 , то при
, то при 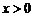 его можно оценить следующим образом:
его можно оценить следующим образом: 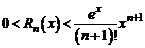 .
.
В частности, при 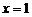 будем иметь
будем иметь
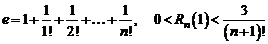 .
.
При 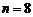 и вычислении с пятью десятичными знаками получим
и вычислении с пятью десятичными знаками получим 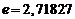 , где верны первые четыре знака, так как ошибка округления не превосходит
, где верны первые четыре знака, так как ошибка округления не превосходит 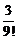 или
или 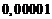 .
.
Если 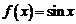 , то из равенств (7.3) получим
, то из равенств (7.3) получим
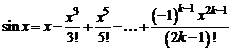 , (3)
, (3)
где остаточный член 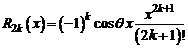 и
и 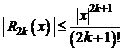 .
.
Для функции 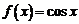 из формулы (7.4) получаем
из формулы (7.4) получаем
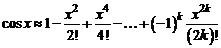 (4)
(4)
Погрешность приближенной формулы (4) оценивается остаточным членом 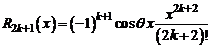 , для которого
, для которого 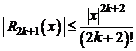 .
.
В частности, для формулы 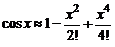 погрешность
погрешность 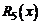 оценивается неравенством
оценивается неравенством 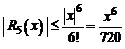 .
.
Для функции 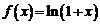 получаем приближенную формулу
получаем приближенную формулу
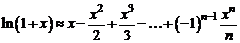 , (5)
, (5)
где остаточный член 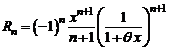 и при
и при 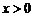 имеет место грубая оценка:
имеет место грубая оценка: 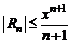 .
.



 имеет производную в точке а, т.е.
имеет производную в точке а, т.е. 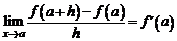 или
или 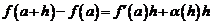 , или
, или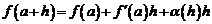 , (1)
, (1)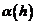 – бесконечно малая функция при
– бесконечно малая функция при 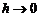 . Поскольку
. Поскольку 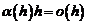 при
при 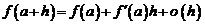 . (2)
. (2)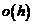 быстрее стремится к нулю, чем h. Если этой величиной пренебречь, то получим следующую приближенную формулу:
быстрее стремится к нулю, чем h. Если этой величиной пренебречь, то получим следующую приближенную формулу: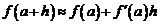 . (3)
. (3)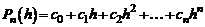 такой, чтобы имело место равенство
такой, чтобы имело место равенство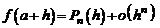 .
. . Многочлен удобен при исследовании функции. Погрешность такой замены будет мала по сравнению с
. Многочлен удобен при исследовании функции. Погрешность такой замены будет мала по сравнению с 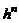 .
.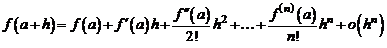 . (4)
. (4) называют остаточным членом формулы Тейлора в форме Пеано. Имеют место и другие выражения для остаточного члена. В частности, если предположить существование
называют остаточным членом формулы Тейлора в форме Пеано. Имеют место и другие выражения для остаточного члена. В частности, если предположить существование  -ой производной в некоторой окрестности точки а, то справедливо равенство
-ой производной в некоторой окрестности точки а, то справедливо равенство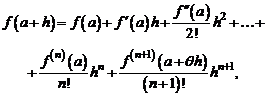 (6)
(6)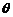 – некоторое число,
– некоторое число, 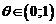 .
.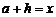 , то формула (4) будет иметь вид
, то формула (4) будет иметь вид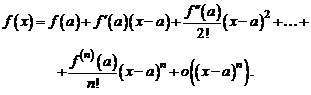 (7)
(7)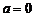 , то получим формулу Маклорена:
, то получим формулу Маклорена: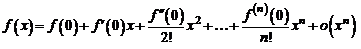 . (8)
. (8)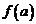 и обозначить
и обозначить 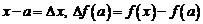 , то будем иметь
, то будем иметь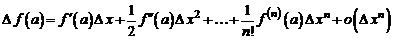 .
.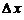 на
на 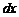 и принимая во внимание формулы (3.1), (3.2), получим
и принимая во внимание формулы (3.1), (3.2), получим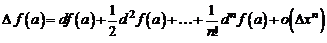 . (9)
. (9)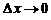 , по приведенной формуле (9) из бесконечно малого приращения
, по приведенной формуле (9) из бесконечно малого приращения 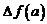 можно выделить не только его главный член – первый дифференциал, но и члены более высокого порядка малости, совпадающие с точностью до факториалов в знаменателях с последовательными дифференциалами
можно выделить не только его главный член – первый дифференциал, но и члены более высокого порядка малости, совпадающие с точностью до факториалов в знаменателях с последовательными дифференциалами 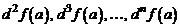 .
.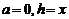 получим формулу Маклорена
получим формулу Маклорена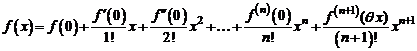 , (1)
, (1)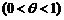 .
.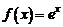 . Имеем
. Имеем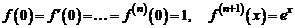 .
.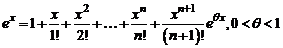 . (2)
. (2)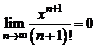 .
.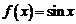 . Имеем
. Имеем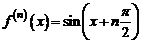 ,
, 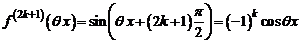 .
.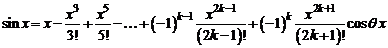 , (3)
, (3)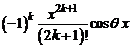 стремится к нулю при
стремится к нулю при  .
.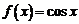 . Поскольку
. Поскольку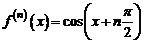 ,
, 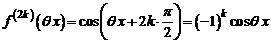 ,
,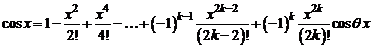 . (4)
. (4)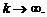
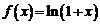 . Имеем
. Имеем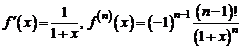 .
.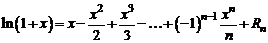 ,
,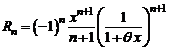 .
.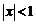 , то
, то 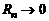 при
при 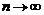 .
.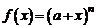 , где а – действительное число, n – натуральное число.
, где а – действительное число, n – натуральное число.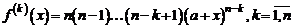 ,
,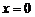 получаем
получаем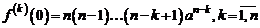 .
.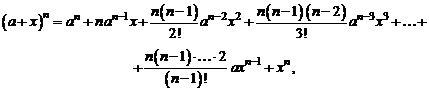
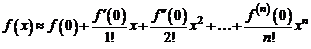 , (1)
, (1) многочленом n- ой степени.
многочленом n- ой степени.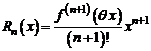 , либо порядком малости этой погрешности
, либо порядком малости этой погрешности 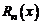 при
при 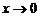 , т. е. она записывается в виде
, т. е. она записывается в виде 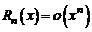 .
.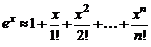 . (2)
. (2)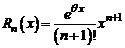 , то при
, то при 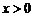 его можно оценить следующим образом:
его можно оценить следующим образом: 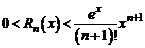 .
.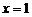 будем иметь
будем иметь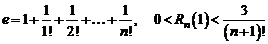 .
.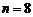 и вычислении с пятью десятичными знаками получим
и вычислении с пятью десятичными знаками получим 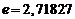 , где верны первые четыре знака, так как ошибка округления не превосходит
, где верны первые четыре знака, так как ошибка округления не превосходит 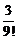 или
или 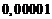 .
.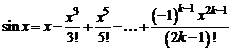 , (3)
, (3)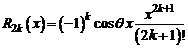 и
и 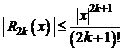 .
.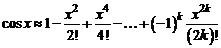 (4)
(4)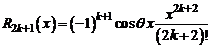 , для которого
, для которого 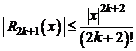 .
.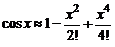 погрешность
погрешность 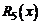 оценивается неравенством
оценивается неравенством 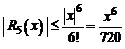 .
.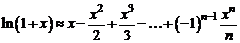 , (5)
, (5)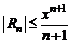 .
.


