Понятие матрицы. Линейные операции над матрицами. Произведение и транспонированием матриц.
10. Понятие матрицы.
Прямоугольная таблица чисел из множества 
 или других однородных элементов называетсяматрицей. Символом
или других однородных элементов называетсяматрицей. Символом  обозначено множество действительных чисел. Для записи матрицы используют (),также квадратные скобки
обозначено множество действительных чисел. Для записи матрицы используют (),также квадратные скобки  или двойные черты
или двойные черты  .
.
Числа  ,
,  называются элементами матрицы.
называются элементами матрицы.
Матрицы обозначаются латинскими буквами A, B, C, D,….
Для обозначения матрицы используются символы 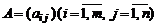
Если матрицы имеют m строк и n столбцов, то говорят, что матрица имеет размерность  .
.
Матрица A квадратная, если 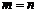 .
.
Главная диагональ  ,
,
побочная диагональ 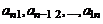 .
.
Если все элементы квадратной матрицы, за исключением элементов главной диагонали равны 0, то матрица называется диагональной.
Матрица 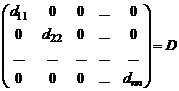 диагональная.
диагональная.
Если 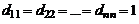 , то диагональная матрица называется единичной и обозначается
, то диагональная матрица называется единичной и обозначается  (или
(или 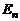 ).
).
Матрицы A и B называются равными  , если они имеют одинаковые размерности и их соответствующие элементы равны
, если они имеют одинаковые размерности и их соответствующие элементы равны 
 .
.
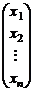 ─ матрица-столбец,
─ матрица-столбец, 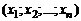 ─ матрица-строка.
─ матрица-строка.
11. Линейные операции над матрицами.
Линейными операциями над матрицами называются сложение и вычитание матриц, умножение матриц на число.
1.Суммой A + B двух матриц  и
и  одинаковых размерностей называется матрица
одинаковых размерностей называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B:
той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B:
 .
.
Свойства сложения
1)  ,
,
2)  ,
,
где A, B, C – произвольные матрицы одинаковых размеров.
2.Произведением матрицы 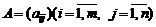 на число
на число 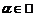 называется матрица
называется матрица 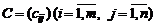 , каждый элемент которой есть произведение соответствующего элемента матрицы A и числа
, каждый элемент которой есть произведение соответствующего элемента матрицы A и числа 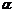 :
:  , т.е.
, т.е.
 .
.
Пример
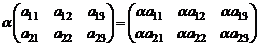 .
.
Свойства
1) 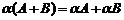 ,
,
2)  ,
,
3) 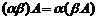 .
.
Здесь  – матрицы одинаковых размерностей, а
– матрицы одинаковых размерностей, а  – действительные числа.
– действительные числа.
3.Разностью  двух матриц
двух матриц  и
и  одинаковых размерностей назовем матрицу
одинаковых размерностей назовем матрицу  такой же размерности, которая определяется по правилу
такой же размерности, которая определяется по правилу
 .
.
Из определений следует, что 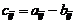 ,
,  .
.
12.Произведение и транспонированием матриц.
Произведением двух матриц А и В, где матрица А имеет размерность mхn, а матрица В имеет размерность nxp, называется матрица С mxp, каждый элемент которой равен сумме произведений элементов i -той строки матрицы А на соответствующий элемент j -го столбца матрицы B:
 ,
, 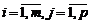 .
.
Пример:
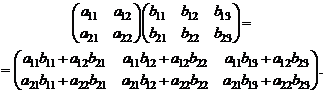
Отметим, что операция умножения двух матриц выполнима тогда и только тогда, когда число столбцов в первом сомножителе равно числу строк во втором.
Свойства
1) 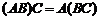 ,
,
2)  ,
,
3)  .
.
Операция умножения матриц не обладает переместительным (коммутативным) свойством. (АВ≠ВА)
Пример.

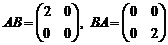 .
.
Если 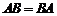 , то матрицы
, то матрицы 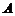 и
и 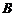 называются перестановочными или коммутирующими между собой.
называются перестановочными или коммутирующими между собой.
Пример.
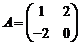 ,
,  .
.
 ,
, 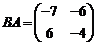 .
.
Матрица  размерности
размерности  называется транспонированной к матрице A размерности
называется транспонированной к матрице A размерности  , если она получена путем замены строк матрицы A столбцами этой же матрицы с теми же номерами:
, если она получена путем замены строк матрицы A столбцами этой же матрицы с теми же номерами:
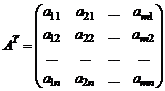 .
.
Свойства:
1) 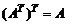 ,
,
2)  ,
,
3) 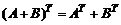 ,
,
4)  .
.
Метод Гаусса.
Распространенным точным методом решения систем линейных алгебраических уравнений является метод Гаусса, который применяется для решения произвольных систем линейных алгебраических уравнений. Суть метода состоит в том, что посредством элементарных преобразований система линейных алгебраических уравнений приводится к треугольной или трапециевидной форме (прямой ход метода Гаусса), при помощи которой непосредственно получаются все решения системы (обратный ход метода Гаусса).
На практике прямой ход метода Гаусса как правило применяется не к системе уравнений, а к ее расширенной матрице 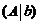 и формализуется следующим образом:
и формализуется следующим образом:
А). Рассмотрим элемент, стоящий в первой строке и в первом столбце матрицы 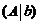 . Если этот элемент оказался равным нулю, то переставляем строки матрицы таким образом, чтобы в первой строке, в первом столбце оказался ненулевой элемент. Обозначим этот элемент через
. Если этот элемент оказался равным нулю, то переставляем строки матрицы таким образом, чтобы в первой строке, в первом столбце оказался ненулевой элемент. Обозначим этот элемент через  и назовем его разрешающим на первом шаге. Пересчитаем элементы матрицы по следующим правилам:
и назовем его разрешающим на первом шаге. Пересчитаем элементы матрицы по следующим правилам:
1) строку, в которой стоит разрешающий элемент, назовем разрешающей; столбец, в котором стоит разрешающий элемент − разрешающим;
2) элементы разрешающей строки и всех вышерасположенных строк (на первом шаге только элементы разрешающей строки) остаются неизменными;
3) элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули;
4) все остальные элементы матрицы вычисляются согласно следующему правилу прямоугольника. Из четырех элементов матрицы составляется прямоугольник таким образом, что разрешающий элемент и элемент, который пересчитывается, образуют главную диагональ этого прямоугольника. Новое значение пересчитываемого элемента вычисляется как разность произведений элементов главной и побочной диагоналей.
Б) В полученной таблице рассмотрим элемент, стоящий во второй строке и втором столбце. Обозначим его через 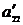 . Будем считать, что выполняется неравенство
. Будем считать, что выполняется неравенство  . В противном случае вторую строку меняем местами со строкой, имеющей больший номер, таким образом, чтобы во второй строке, втором столбце оказался ненулевой элемент. Если во втором столбце и рассматриваемых строках не нашлось ненулевого элемента, то переставляем местами второй столбец и столбец с большим номером таким образом, чтобы элемент, стоящий во второй строке, втором столбце, не был равен нулю. Теперь назовем элемент
. В противном случае вторую строку меняем местами со строкой, имеющей больший номер, таким образом, чтобы во второй строке, втором столбце оказался ненулевой элемент. Если во втором столбце и рассматриваемых строках не нашлось ненулевого элемента, то переставляем местами второй столбец и столбец с большим номером таким образом, чтобы элемент, стоящий во второй строке, втором столбце, не был равен нулю. Теперь назовем элемент 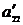 − разрешающим на этом шаге и пересчитаем элементы матрицы по правилам 1)-4).
− разрешающим на этом шаге и пересчитаем элементы матрицы по правилам 1)-4).
В) Применяем правила 1)-4), двигаясь по строкам матрицы вниз, выбирая в качестве разрешающего элемента ненулевой элемент, стоящий на пересечении стоки и столбца с номерами, совпадающими с номером шага. Если в процессе преобразований образуется строка, состоящая из нулей, то эту строку удаляем.
Для выполнения обратного хода метода Гаусса возвращаемся от преобразованной матрицы системы к системе уравнений. При этом, если в процессе прямого хода метода производилась перестановка столбцов, то в системе, соответствующей преобразованной матрице, должно быть выполнено соответствующее переименование переменных.
Если в полученной системе встретится уравнение вида  , где
, где  , то исходная система несовместна. В противном случае − совместна.
, то исходная система несовместна. В противном случае − совместна.
Совместная система после преобразований имеет вид:
 (1)
(1)
где коэффициенты  отличны от нуля. Для произвольной системы справедливы неравенства
отличны от нуля. Для произвольной системы справедливы неравенства  . Неравенство
. Неравенство 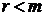 выполняется в тех случаях, когда в процессе прямого хода метода удалялись нулевые строки (т.е. удалялись уравнения вида
выполняется в тех случаях, когда в процессе прямого хода метода удалялись нулевые строки (т.е. удалялись уравнения вида  .)
.)
В процессе обратного хода метода Гаусса находятся все решения системы. Если в системе (1)  , то она имеет треугольный вид. Из последнего уравнения
, то она имеет треугольный вид. Из последнего уравнения  находим
находим  , из предпоследнего –
, из предпоследнего –  и т.д. и, наконец, из первого –
и т.д. и, наконец, из первого –  ,и, тем самым, – единственное решение исходной системы.
,и, тем самым, – единственное решение исходной системы.
Если  , то в результате обратного хода r неизвестных можно выразить линейно через остальные
, то в результате обратного хода r неизвестных можно выразить линейно через остальные  неизвестных. Эти r неизвестных называют базисными, а остальные
неизвестных. Эти r неизвестных называют базисными, а остальные  – свободными. В результате получим общее решение системы в виде:
– свободными. В результате получим общее решение системы в виде:
 (5)
(5)
Чтобы получить какое-нибудь частное решение исходной системы, нужно придать свободным неизвестным некоторые числовые значения. Ясно, что в случае r < п система имеет бесконечное множество решений.
Эллипс. Его характеристики.
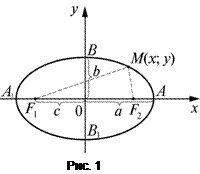 Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек 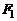 и
и  , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная  .
.
Выберем декартову систему координат  так, чтобы ось
так, чтобы ось  проходила через фокусы
проходила через фокусы 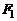 и
и  , расстояние между которыми обозначим
, расстояние между которыми обозначим 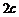 , а начало координат О находилось в середине отрезка
, а начало координат О находилось в середине отрезка  (рис. 1). В такой системе координат уравнение эллипса будетиметь вид
(рис. 1). В такой системе координат уравнение эллипса будетиметь вид
 . (1)
. (1)
Уравнение (1) называется каноническим уравнением эллипса. Параметр 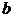 определяется равенством
определяется равенством  . Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось
. Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось  в двух точках:
в двух точках:  и
и 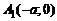 ; пересекает ось
; пересекает ось 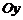 в двух точках:
в двух точках:  и
и 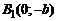 . Эти четыре точки называют вершинами эллипса. Отрезок
. Эти четыре точки называют вершинами эллипса. Отрезок  называется большой осью эллипса, а отрезок
называется большой осью эллипса, а отрезок  – его малой осью. Здесь
– его малой осью. Здесь  .
.
Уравнение (1) можно рассматривать и в случае  тогда оно определяет эллипс с большой полуосью
тогда оно определяет эллипс с большой полуосью  фокусы такого эллипса лежат на оси Oy.
фокусы такого эллипса лежат на оси Oy.
В случае, когда  , уравнение (1) имеет вид
, уравнение (1) имеет вид  и определяет окружность радиуса а с центром в начале координат. В этом случае
и определяет окружность радиуса а с центром в начале координат. В этом случае 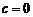 .
.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси, т.е.
 .
.
Поскольку 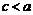 , то для любого эллипса
, то для любого эллипса 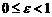 , причем случай
, причем случай  соответствует окружности.
соответствует окружности.
Геометрически  характеризует степень сжатия эллипса: чем больше
характеризует степень сжатия эллипса: чем больше  , тем больше вытянут эллипс.
, тем больше вытянут эллипс.
Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии 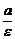 от него, называются директрисами эллипса.
от него, называются директрисами эллипса.
Если эллипс задан каноническим уравнением (1), то уравнения директрис имеют вид
 и
и 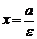 .
.
Так как  , то
, то  . Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины.
. Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины.
Кониченские поверхности.
Конической называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и проходящей через некоторую точку (вершину). Уравнение конуса второго порядка с вершиной в начале координат, осью которого служит ось Oz, записывается в виде
 . (5)
. (5)
Геометрически коническую поверхность можно изобразить, как показано на рис. 4.
Аналогично, уравнения  ,
,  являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
Цилиндрические поверхности.
Поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной некоторому заданному направлению, называется цилиндрической.
Уравнение вида  в декартовой системе координат
в декартовой системе координат
в пространстве определяет цилиндрическую поверхность, у которой образующие параллельны оси Oz. Аналогично, уравнение  определяет цилиндрическую поверхность с образующими параллельными оси Oy, а
определяет цилиндрическую поверхность с образующими параллельными оси Oy, а  – цилиндрическую поверхность с образующими параллельными оси Ох.
– цилиндрическую поверхность с образующими параллельными оси Ох.
Канонические уравнения цилиндров второго порядка:
эллиптический цилиндр
 , (2)
, (2)
гиперболический цилиндр
 , (3)
, (3)
параболический цилиндр
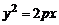 . (4)
. (4)
Образующие всех трех цилиндров, определяемых уравнениями (2), (3), (4), параллельны оси Oz, а направляющей служит соответствующая кривая второго порядка (эллипс, гипербола, парабола), лежащая в плоскости Oxy.
Отметим, что кривую в пространстве можно задать либо параметрически, либо в виде линии пересечения двух поверхностей. Например, уравнения направляющей эллиптического цилиндра, т.е. уравнения эллипса в плоскости Oxy, имеют вид
 .
.
Эллипсоид.
Эллипсоидом (рис. 1) называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением

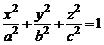 , (1)
, (1)
где величины а, b, c называют полуосями эллипсоида.
Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат – центром симметрии.
Точки пересечения осей координат с эллипсоидом называют вершинами эллипсоида.
Рассмотрим сечение эллипсоида плоскостью 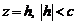 , параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
, параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
 . (2)
. (2)
Обозначим  и перепишем (2) в виде
и перепишем (2) в виде  .
.
Таким образом, сечение эллипсоида (1) плоскостью  , представляет собой эллипс с полуосями ak и bk. Если
, представляет собой эллипс с полуосями ak и bk. Если  , то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+ с) или
, то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+ с) или  .
.
Аналогичная картина получается при рассмотрении сечений эллипсоида плоскостями, параллельными координатным плоскостям Oxz и Oyz. Заметим только, что плоскость Oхz пересекает эллипсоид по эллипсу, который определяется системой
 ,
,
плоскость Oyz – по эллипсу, определяемому уравнениями
 .
.
Если две полуоси эллипсоида равны, например  , из (1) получаем уравнение
, из (1) получаем уравнение
 (3)
(3)
Если пересечь эллипсоид (3) плоскостью  , то получим окружность
, то получим окружность

с центром на оси Oz. Поэтому такой эллипсоид можно получить вращением расположенного в плоскости Oхz эллипса  вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения.
вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения.
Отметим также, что в случае  эллипсоид является сферой.
эллипсоид является сферой.
Гиперболоиды.
Однополостным гиперболоидом называется поверхность, которая в декартовой системе координат Oxyz определяется каноническим уравнением
 . (1)
. (1)
Установим форму поверхности (1). Для этого рассмотрим сечения ее координатными плоскостями Oxz и Oyz. Получаем соответственно системы уравнений:

 (2)
(2)
 Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz.
Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz.
Рассмотрим теперь сечения данного гиперболоида плоскостями z = h, параллельными координатной плоскости Оху. В сечениях получим линии, определяемые системой уравнений
 (3)
(3)
Введя величины  и
и 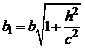 , перепишем систему (3) в виде
, перепишем систему (3) в виде
 (
( )
)
Из ( ) заключаем, что плоскость
) заключаем, что плоскость  пересекает гиперболоид по эллипсу с полуосями а 1 и b 1.
пересекает гиперболоид по эллипсу с полуосями а 1 и b 1.
Рассмотренные сечения показывают, что однополостный гиперболоид изображается в виде бесконечной трубки, бесконечно расширяющейся в обе стороны по мере удаления от плоскости Оху (рис. 1).
Величины a, b, c называются полуосями однополостного гиперболоида.
Двуполостным гиперболоидом называют поверхность, определяемую в декартовой системе координат Oxyz каноническим уравнением
 . (4)
. (4)
Для установления формы поверхности (4) рассмотрим сечения этой поверхности координатными плоскостями Oxz и Oyz. Получим соответственно системы уравнений
 и
и 
из которых вытекает, что сечения представляются гиперболами. Изучим теперь сечения гиперболоида (1) плоскостями  . В сечениях получаем линии
. В сечениях получаем линии
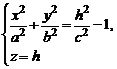 или
или  (5)
(5)
 где
где 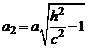 и
и  .
.
При  плоскость
плоскость  пересекает гиперболоид по эллипсу с полуосями а 2 и b 2, причем при увеличении
пересекает гиперболоид по эллипсу с полуосями а 2 и b 2, причем при увеличении 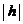 величины а 2 и b 2 также увеличиваются.
величины а 2 и b 2 также увеличиваются.
Если  , то из системы (5) получаем только две точки: (0;0;+ с) и
, то из системы (5) получаем только две точки: (0;0;+ с) и  , и поэтому плоскости
, и поэтому плоскости  касаются данной поверхности.
касаются данной поверхности.
При 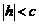 система (5) определяет мнимый эллипс, т.е. плоскость
система (5) определяет мнимый эллипс, т.е. плоскость  не пересекается с гиперболоидом (4).
не пересекается с гиперболоидом (4).
Рассмотренные сечения позволяют изобразить двуполостный гиперболоид в виде поверхности, состоящей из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши (рис. 2).
Величины a, b, c называют полуосями двуполостного гиперболоида. Если полуоси  и
и 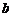 гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси
гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси 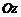 гиперболы
гиперболы  в случае однополостного гиперболоида и гиперболы
в случае однополостного гиперболоида и гиперболы 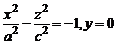 в случае двуполостного гиперболоида.
в случае двуполостного гиперболоида.
Параболоиды.
Эллиптическим параболоидом (рис. 1) называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением
 (1)
(1)
Гиперболическим параболоидом (рис. 2) называется поверхность, определяемая каноническим уравнением
 (2)
(2)

Рис. 1. Рис. 2.
Из уравнений (1) и (2) вытекает, что плоскости Oxz и Oyz являются плоскостями симметрии параболоидов.
Ось Oz называется осью параболоида, а точка ее пересечения с поверхностью параболоида – вершиной.
Оба параболоида плоскостями, параллельными координатным плоскостям Oxz и Oyz, пересекаются по параболам. Например, плоскость 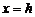 пересекает эллиптический параболоид по параболе
пересекает эллиптический параболоид по параболе
 .
.
Из уравнения (1) заключаем, что плоскость  , параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
, параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
 ,
,
где  и
и  . Из уравнения (2) получаем, что плоскость
. Из уравнения (2) получаем, что плоскость  пересекает гиперболический параболоид по гиперболе
пересекает гиперболический параболоид по гиперболе
 .
.
Плоскость Оху пересекает гиперболический параболоид по двум пересекающимся прямым
 .
.
При  эллиптический параболоид, заданный уравнением
эллиптический параболоид, заданный уравнением
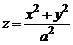 ,
,
называется параболоидом вращения. Он получается при вращении параболы  вокруг оси Oz.
вокруг оси Oz.
25. Линейное векторное пространство. Подпространство. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов. Преобразование координат вектора при замене базиса.
251. Линейное векторное пространство.
Рассмотрим множество  элементов
элементов  и множество
и множество  действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам
действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам  поставим в соответствии третий элемент
поставим в соответствии третий элемент  , называемый их суммой
, называемый их суммой  , и операцию умножения на действительные числа (внешнюю операцию): каждому элементу
, и операцию умножения на действительные числа (внешнюю операцию): каждому элементу 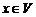 и
и 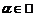 поставим в соответствие элемент
поставим в соответствие элемент 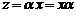 , где
, где  . Потребуем, чтобы для любых элементов
. Потребуем, чтобы для любых элементов 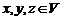 и чисел
и чисел  были выполнены следующие аксиомы:
были выполнены следующие аксиомы:
1.  – коммутативный закон.
– коммутативный закон.
2.  – ассоциативный закон.
– ассоциативный закон.
3. Существует такой элемент  (называемый нулевым элементом), что
(называемый нулевым элементом), что 
4. Для каждого элемента 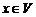 существует такой элемент
существует такой элемент  (называемый элементом, противоположным элементу
(называемый элементом, противоположным элементу 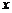 ), что
), что  .
.
5. Существует элемент 1, называемый единичным, такой, что  .
.
6.  .
.
7. 
8.  .
.
Множество 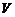 , в котором определены операции сложения элементов и умножения элемента на действительное число, удовлетворяющие аксиомам 1 – 8, называется действительным (вещественным) линейным пространством или действительным (вещественным) векторным пространством, а его элементы называются векторами.
, в котором определены операции сложения элементов и умножения элемента на действительное число, удовлетворяющие аксиомам 1 – 8, называется действительным (вещественным) линейным пространством или действительным (вещественным) векторным пространством, а его элементы называются векторами.
Отметим, что сумму 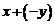 обозначают
обозначают  и называют разностью элементов
и называют разностью элементов 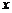 и
и 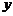 .
.
Примеры линейных пространств.
1. Множество всех свободных векторов  , где
, где  , для которых определены сложение и умножение вектора на число, является линейным пространством
, для которых определены сложение и умножение вектора на число, является линейным пространством 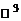 . В этом пространстве роль нулевого элемента играет нулевой вектор
. В этом пространстве роль нулевого элемента играет нулевой вектор  ; противоположным вектору
; противоположным вектору  является вектор
является вектор  .
.
2. Линейное пространство образует также множество всех матриц  заданного порядка
заданного порядка  , для которых определены операции сложения и умножения на число. Здесь роль нулевого элемента играет нулевая матрица, а противоположной к матрице
, для которых определены операции сложения и умножения на число. Здесь роль нулевого элемента играет нулевая матрица, а противоположной к матрице 
 будет матрица
будет матрица 
 .
.
3. Множество алгебраических многочленов от одной переменной степени не выше n. Нулевой вектор есть многочлен с коэффициентами, равными нулю.
4. множество всех матриц-столбцов длины n.
252. Подпространство.
Пусть задано множество  , в котором определены те же операции, что и в линейном пространстве
, в котором определены те же операции, что и в линейном пространстве 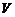 . Множество
. Множество  назовем подпространством линейного пространства
назовем подпространством линейного пространства 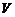 , если выполнены следующие условия: 1) если
, если выполнены следующие условия: 1) если 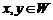 , то
, то  ; 2) если
; 2) если  , то
, то  .
.
Очевидно, что всякое подпространство  линейного пространства
линейного пространства 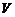 является линейным пространством. В
является линейным пространством. В  есть нулевой элемент 0: если
есть нулевой элемент 0: если  , то
, то  . Для любого элемента
. Для любого элемента  имеется противоположный элемент
имеется противоположный элемент  : если
: если  , то
, то  . Отметим, что нулевой элемент 0 линейного пространства
. Отметим, что нулевой элемент 0 линейного пространства 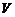 образует подпространство данного пространства V, а само пространство
образует подпространство данного пространства V, а само пространство 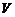 можно рассматривать как подпространство этого пространства. Такие подпространства называют тривиальными, а все другие, если они имеются, нетривиальными.
можно рассматривать как подпространство этого пространства. Такие подпространства называют тривиальными, а все другие, если они имеются, нетривиальными.
Например, множество  всех свободных векторов
всех свободных векторов 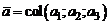 , параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства.
, параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства.
253. Линейная зависимость и независимость векторов линейного пространства.
Пусть  - элементы линейного пространства, а
- элементы линейного пространства, а  – вещественные числа.
– вещественные числа.
Вектор  назовем линейной комбинацией векторов
назовем линейной комбинацией векторов  . Если все
. Если все  , то линейная комбинация называется тривиальной; если хотя бы одно из чисел
, то линейная комбинация называется тривиальной; если хотя бы одно из чисел 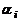 отлично от нуля, то линейная комбинация называется нетривиальной.
отлично от нуля, то линейная комбинация называется нетривиальной.
Система векторов  называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е.
называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е.
 (1)
(1)
Если равенство (1) выполняется только в случае  , то система векторов
, то система векторов  называется линейно независимой.
называется линейно независимой.
Введем понятия коллинеарности и компланарности векторов линейного пространства.
Два вектора 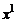 и
и 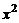 назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора
назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора 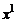 ,
, 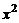 ,
,  называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.
называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.
254. Базис и размерность линейного пространства.
Линейное пространство называется конечномерным, если существует такое натуральное число n, что в этом пространстве найдетсясистемаиз n линейно независимых векторов, а любая система из (n+1) вектора является линейно зависимой. Число n в этом случае называется размерностью пространства.
Базисом 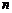 -мерного линейного пространства
-мерного линейного пространства 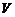 называется любая упорядоченная система
называется любая упорядоченная система 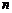 линейно независимых векторов этого пространства. Например, базис пространства
линейно независимых векторов этого пространства. Например, базис пространства 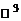 образует любая упорядоченная тройка некомпланарных векторов этого пространства.
образует любая упорядоченная тройка некомпланарных векторов этого пространства.
Система 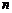 векторов
векторов  есть базис пространства
есть базис пространства 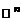 .
.
255. Координаты векторов.
Теорема 1. Пусть 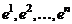 - некоторый базис линейного
- некоторый базис линейного
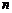 -мерного пространства
-мерного пространства 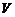 . Тогда любой вектор
. Тогда любой вектор 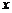 этого пространства линейно выражается через базисные векторы
этого пространства линейно выражается через базисные векторы 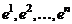 , т.е.
, т.е.
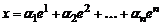 , (5)
, (5)
причем коэффициенты  в разложении (5) определяются однозначно.
в разложении (5) определяются однозначно.
Выражение (5) называется разложением вектора 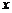 по базису
по базису 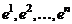 , а коэффициенты
, а коэффициенты  – координатами вектора
– координатами вектора 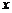 в базисе
в базисе 
|
|
|



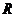
 или других однородных элементов называетсяматрицей. Символом
или других однородных элементов называетсяматрицей. Символом  или двойные черты
или двойные черты 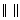 .
. ,
,  называются элементами матрицы.
называются элементами матрицы.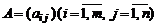
 .
.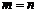 .
. ,
,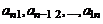 .
.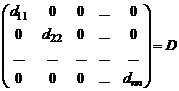 диагональная.
диагональная.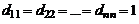 , то диагональная матрица называется единичной и обозначается
, то диагональная матрица называется единичной и обозначается  (или
(или 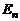 ).
). , если они имеют одинаковые размерности и их соответствующие элементы равны
, если они имеют одинаковые размерности и их соответствующие элементы равны 
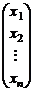 ─ матрица-столбец,
─ матрица-столбец, 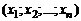 ─ матрица-строка.
─ матрица-строка. и
и  одинаковых размерностей называется матрица
одинаковых размерностей называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B:
той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B: .
. ,
, ,
,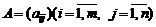 на число
на число 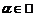 называется матрица
называется матрица 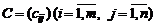 , каждый элемент которой есть произведение соответствующего элемента матрицы A и числа
, каждый элемент которой есть произведение соответствующего элемента матрицы A и числа 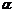 :
:  , т.е.
, т.е. .
.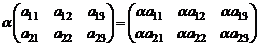 .
.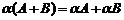 ,
, ,
,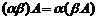 .
. – матрицы одинаковых размерностей, а
– матрицы одинаковых размерностей, а  – действительные числа.
– действительные числа. двух матриц
двух матриц  .
.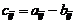 ,
,  .
. ,
, 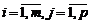 .
.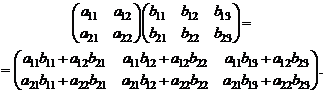
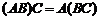 ,
, ,
, .
.
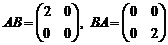 .
.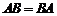 , то матрицы
, то матрицы 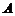 и
и 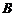 называются перестановочными или коммутирующими между собой.
называются перестановочными или коммутирующими между собой.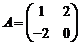 ,
,  .
. ,
, 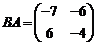 .
. размерности
размерности  называется транспонированной к матрице A размерности
называется транспонированной к матрице A размерности 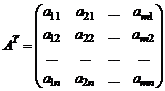 .
.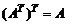 ,
, ,
,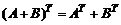 ,
, .
.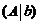 и формализуется следующим образом:
и формализуется следующим образом: и назовем его разрешающим на первом шаге. Пересчитаем элементы матрицы по следующим правилам:
и назовем его разрешающим на первом шаге. Пересчитаем элементы матрицы по следующим правилам: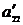 . Будем считать, что выполняется неравенство
. Будем считать, что выполняется неравенство  . В противном случае вторую строку меняем местами со строкой, имеющей больший номер, таким образом, чтобы во второй строке, втором столбце оказался ненулевой элемент. Если во втором столбце и рассматриваемых строках не нашлось ненулевого элемента, то переставляем местами второй столбец и столбец с большим номером таким образом, чтобы элемент, стоящий во второй строке, втором столбце, не был равен нулю. Теперь назовем элемент
. В противном случае вторую строку меняем местами со строкой, имеющей больший номер, таким образом, чтобы во второй строке, втором столбце оказался ненулевой элемент. Если во втором столбце и рассматриваемых строках не нашлось ненулевого элемента, то переставляем местами второй столбец и столбец с большим номером таким образом, чтобы элемент, стоящий во второй строке, втором столбце, не был равен нулю. Теперь назовем элемент  , где
, где  , то исходная система несовместна. В противном случае − совместна.
, то исходная система несовместна. В противном случае − совместна. (1)
(1) отличны от нуля. Для произвольной системы справедливы неравенства
отличны от нуля. Для произвольной системы справедливы неравенства  . Неравенство
. Неравенство 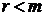 выполняется в тех случаях, когда в процессе прямого хода метода удалялись нулевые строки (т.е. удалялись уравнения вида
выполняется в тех случаях, когда в процессе прямого хода метода удалялись нулевые строки (т.е. удалялись уравнения вида  .)
.) , то она имеет треугольный вид. Из последнего уравнения
, то она имеет треугольный вид. Из последнего уравнения  находим
находим  , из предпоследнего –
, из предпоследнего –  и т.д. и, наконец, из первого –
и т.д. и, наконец, из первого –  ,и, тем самым, – единственное решение исходной системы.
,и, тем самым, – единственное решение исходной системы. , то в результате обратного хода r неизвестных можно выразить линейно через остальные
, то в результате обратного хода r неизвестных можно выразить линейно через остальные  неизвестных. Эти r неизвестных называют базисными, а остальные
неизвестных. Эти r неизвестных называют базисными, а остальные  (5)
(5) Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек 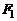 и
и  , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная  .
. так, чтобы ось
так, чтобы ось  проходила через фокусы
проходила через фокусы 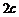 , а начало координат О находилось в середине отрезка
, а начало координат О находилось в середине отрезка  (рис. 1). В такой системе координат уравнение эллипса будетиметь вид
(рис. 1). В такой системе координат уравнение эллипса будетиметь вид . (1)
. (1)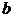 определяется равенством
определяется равенством  . Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось
. Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось  и
и 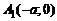 ; пересекает ось
; пересекает ось 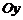 в двух точках:
в двух точках:  и
и 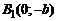 . Эти четыре точки называют вершинами эллипса. Отрезок
. Эти четыре точки называют вершинами эллипса. Отрезок  называется большой осью эллипса, а отрезок
называется большой осью эллипса, а отрезок  – его малой осью. Здесь
– его малой осью. Здесь  .
. тогда оно определяет эллипс с большой полуосью
тогда оно определяет эллипс с большой полуосью  фокусы такого эллипса лежат на оси Oy.
фокусы такого эллипса лежат на оси Oy. , уравнение (1) имеет вид
, уравнение (1) имеет вид  и определяет окружность радиуса а с центром в начале координат. В этом случае
и определяет окружность радиуса а с центром в начале координат. В этом случае 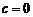 .
. .
.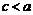 , то для любого эллипса
, то для любого эллипса 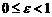 , причем случай
, причем случай  соответствует окружности.
соответствует окружности. характеризует степень сжатия эллипса: чем больше
характеризует степень сжатия эллипса: чем больше 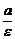 от него, называются директрисами эллипса.
от него, называются директрисами эллипса. и
и 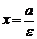 .
. , то
, то  . Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины.
. Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины. . (5)
. (5) ,
,  являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох. в декартовой системе координат
в декартовой системе координат  определяет цилиндрическую поверхность с образующими параллельными оси Oy, а
определяет цилиндрическую поверхность с образующими параллельными оси Oy, а  – цилиндрическую поверхность с образующими параллельными оси Ох.
– цилиндрическую поверхность с образующими параллельными оси Ох. , (2)
, (2) , (3)
, (3)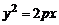 . (4)
. (4) .
.
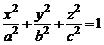 , (1)
, (1)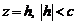 , параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
, параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений: . (2)
. (2) и перепишем (2) в виде
и перепишем (2) в виде  .
. , представляет собой эллипс с полуосями ak и bk. Если
, представляет собой эллипс с полуосями ak и bk. Если  , то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+ с) или
, то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+ с) или  .
. ,
, .
. , из (1) получаем уравнение
, из (1) получаем уравнение (3)
(3) , то получим окружность
, то получим окружность
 вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения.
вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения. эллипсоид является сферой.
эллипсоид является сферой. . (1)
. (1)
 (2)
(2) Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz.
Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz. (3)
(3) и
и 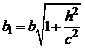 , перепишем систему (3) в виде
, перепишем систему (3) в виде (
( )
) . (4)
. (4) и
и 
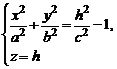 или
или  (5)
(5) где
где 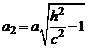 и
и  .
. плоскость
плоскость 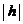 величины а 2 и b 2 также увеличиваются.
величины а 2 и b 2 также увеличиваются. касаются данной поверхности.
касаются данной поверхности.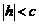 система (5) определяет мнимый эллипс, т.е. плоскость
система (5) определяет мнимый эллипс, т.е. плоскость  и
и 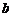 гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси
гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси 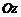 гиперболы
гиперболы  в случае однополостного гиперболоида и гиперболы
в случае однополостного гиперболоида и гиперболы 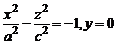 в случае двуполостного гиперболоида.
в случае двуполостного гиперболоида. (1)
(1) (2)
(2)
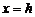 пересекает эллиптический параболоид по параболе
пересекает эллиптический параболоид по параболе .
. , параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
, параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу ,
, и
и  . Из уравнения (2) получаем, что плоскость
. Из уравнения (2) получаем, что плоскость  пересекает гиперболический параболоид по гиперболе
пересекает гиперболический параболоид по гиперболе .
. .
.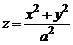 ,
, вокруг оси Oz.
вокруг оси Oz.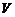 элементов
элементов  и множество
и множество  действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам
действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам  поставим в соответствии третий элемент
поставим в соответствии третий элемент  , называемый их суммой
, называемый их суммой  , и операцию умножения на действительные числа (внешнюю операцию): каждому элементу
, и операцию умножения на действительные числа (внешнюю операцию): каждому элементу 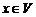 и
и 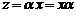 , где
, где 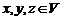 и чисел
и чисел  были выполнены следующие аксиомы:
были выполнены следующие аксиомы: – коммутативный закон.
– коммутативный закон. – ассоциативный закон.
– ассоциативный закон. (называемый нулевым элементом), что
(называемый нулевым элементом), что 
 (называемый элементом, противоположным элементу
(называемый элементом, противоположным элементу 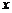 ), что
), что  .
. .
. .
.
 .
.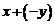 обозначают
обозначают  и называют разностью элементов
и называют разностью элементов 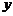 .
. , где
, где  , для которых определены сложение и умножение вектора на число, является линейным пространством
, для которых определены сложение и умножение вектора на число, является линейным пространством 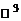 . В этом пространстве роль нулевого элемента играет нулевой вектор
. В этом пространстве роль нулевого элемента играет нулевой вектор  ; противоположным вектору
; противоположным вектору  является вектор
является вектор  .
. заданного порядка
заданного порядка 
 будет матрица
будет матрица 
 .
. , в котором определены те же операции, что и в линейном пространстве
, в котором определены те же операции, что и в линейном пространстве  назовем подпространством линейного пространства
назовем подпространством линейного пространства 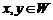 , то
, то  ; 2) если
; 2) если  , то
, то  .
. . Для любого элемента
. Для любого элемента  : если
: если  . Отметим, что нулевой элемент 0 линейного пространства
. Отметим, что нулевой элемент 0 линейного пространства 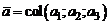 , параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства.
, параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства. - элементы линейного пространства, а
- элементы линейного пространства, а  – вещественные числа.
– вещественные числа. назовем линейной комбинацией векторов
назовем линейной комбинацией векторов  , то линейная комбинация называется тривиальной; если хотя бы одно из чисел
, то линейная комбинация называется тривиальной; если хотя бы одно из чисел 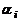 отлично от нуля, то линейная комбинация называется нетривиальной.
отлично от нуля, то линейная комбинация называется нетривиальной. (1)
(1) , то система векторов
, то система векторов 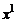 и
и 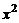 назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора
назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора  называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.
называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.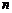 -мерного линейного пространства
-мерного линейного пространства  есть базис пространства
есть базис пространства 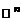 .
.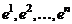 - некоторый базис линейного
- некоторый базис линейного 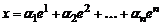 , (5)
, (5)