Х – обл-ть опред-я ф-ции
х1, х2… хn – независ-е переем-е (аргументы)
Z – ф-ция Пример: Z=П х21*х2 (Объем цилиндра)
Рассм-м Z=f(х;у) – ф-цию 2-х перем-х (х1, х2 замен-ся на х,у). Рез-ты по аналогии переносятся на др. ф-ции многих перем-х. Обл-ть опред-я ф-ции 2-х перем-х – вся корд пл-ть (оху) или ее часть. Мн-во знач-й ф-ции 2-х перем-х – поверх-ть в 3х-мерном простр-ве.
Приемы построения графиков: - Рассм-т сечение поверх-ти пл-тями || координатным пл-тям.
Пример: х = х0, зн. пл-ть Х || 0уz у = у0 0хz Вид ф-ции: Z=f(х0,y); Z=f(x,у0)
Например: Z=x2+y2-2y
Z= x2+(y-1)2-1 x=0 Z=(y-1)2-1 y=1 Z= x2-1 Z=0 x2+(y-1)2-1
Парабола окруж-ть(центр(0;1)
1б .Пределы и непрерывность ф-ций двух переменных
Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.(х0,y0), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,у удовл-щих |x-х0|<б; |y-y0|<б выполняется нерав-во |f(x,y)-A|<E
Z=f(х;у) непрерывна в т.(х0,y0), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х0 и у к у0; - этот предел = знач-ю
ф-ции в т.(х0,y0), т.е. limf(х;у)=f(х0,y0)
Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

2. Частные производные первого и второго порядка
Производная первого порядка(которая называется частной) Пусть 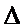 х,
х, 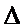 у – приращения независимых переменных х и у в некоторой точке из области Х. Тогда величина, равная
у – приращения независимых переменных х и у в некоторой точке из области Х. Тогда величина, равная  z = f(x+
z = f(x+  х, y+
х, y+  у) = f(x,y) называется полным приращением в точке х0,у0.Если переменную х зафиксировать, а переменной у дать приращение
у) = f(x,y) называется полным приращением в точке х0,у0.Если переменную х зафиксировать, а переменной у дать приращение  у, то получим
у, то получим  zу = f(x,y,+
zу = f(x,y,+  у) – f(x,y). Аналогично определяется частная производная от переменной у, т.е.
у) – f(x,y). Аналогично определяется частная производная от переменной у, т.е.
z’x = 
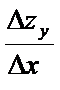
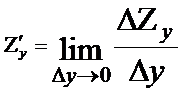 Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.
Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.
Отличие состоит в том, что при дифференциации функции по переменной х, у считается const, а при дифференцировании по у, х считается const.
Для ф-и 2-х переем-х сущ 4 части произв-х 2 порядка: 
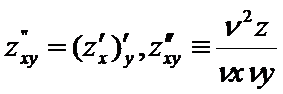
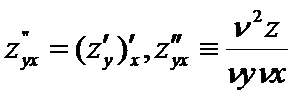
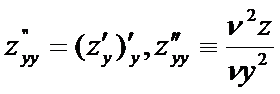
3. Полный дифференциал функции 2-х переменных
Пусть z = f(x,y), тогда dz =  - наз полным дифференциалом
- наз полным дифференциалом
Учитывая, что для ф-и f(x,y)=x, f(x,y)=y, df(x,y)=∆x=dx, df(x,y)=∆y=dy, полный диф-л можно записать в виде:
Геометрич смысл. О. Т.  наз max(min) ф-и z = f(x,y), если сущ некот окрест-ть т.
наз max(min) ф-и z = f(x,y), если сущ некот окрест-ть т. 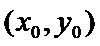 такая, что для всех x,y из этой окрест-ти вып-ся нер-во f(x,y)<f
такая, что для всех x,y из этой окрест-ти вып-ся нер-во f(x,y)<f 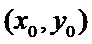 (max) или f(x,y)>f
(max) или f(x,y)>f  (min). Т.: Если задана точка экс-ма ф-и 2-х переем-х, то знач-е частных произв-х в этой точке = 0, т.е.
(min). Т.: Если задана точка экс-ма ф-и 2-х переем-х, то знач-е частных произв-х в этой точке = 0, т.е. 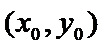 ,
, 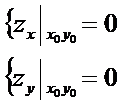
Точки 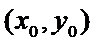 , в которых частные производные первого порядка называются стационарными или критическими.
, в которых частные производные первого порядка называются стационарными или критическими.
Поэтому для нахождения точек экстремума функции 2-х переменных используются достаточные условия экстремума.
Достат усл-е экстр-ма: Пусть функция z = f(x,y) дважды дифференцируема, и 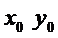 стационарная точка,
стационарная точка,
A = 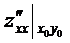 , B =
, B =  , C =
, C =  ,
,  , тогда
, тогда
1)  , причем max, если A<0, min, если A>0.
, причем max, если A<0, min, если A>0.
2) 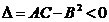 , экстр-ма в т.
, экстр-ма в т. 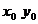 нет
нет
3) 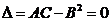 , треб-ся доп исслед-е
, треб-ся доп исслед-е
приближ выч-ях знач-й ф-и 2-х переем-х, исп-ся след формула: 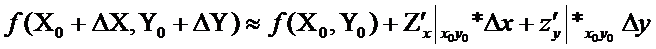
4 .Экстремум функции двух переменных
На практике часто приходится решать задачи сглаживанию эксперимент завис-тей.
I этап
Устанавливается вид зависимости y = f(x) (линейная, квадратичная, логарифмическая и т.д.).
II этап
Опред-ся неизв пар-ры этой ф-ии. Для этого применяют наиболее распр и теоретически обоснованный метод наименьших квадратов. Он состоит в следующем:
В кач-ве неизв пар-ра ф-и f(x) выб-т такие знач-я, чтобы суммы кв-тов невязок ( ) была мин. Невязка (
) была мин. Невязка ( ) – это –откл-е от «теоретич» знач-й
) – это –откл-е от «теоретич» знач-й  , найд по эмпирич формулам y = f(x) от соответствующих опытных знач-й
, найд по эмпирич формулам y = f(x) от соответствующих опытных знач-й  . Рассм-м функцию
. Рассм-м функцию  (т.е. сумму квадратов всех невязок) Пусть в кач-ве ф-и у = f(x) взята лин ф-я у = ax + b. Тогда задание сводится к отыскиванию пар-ов a и b, при кот ф-я
(т.е. сумму квадратов всех невязок) Пусть в кач-ве ф-и у = f(x) взята лин ф-я у = ax + b. Тогда задание сводится к отыскиванию пар-ов a и b, при кот ф-я  принимает наим зн-е. Очевидно, что S = S(a,b) есть ф-я 2-х переем-х a и b, а
принимает наим зн-е. Очевидно, что S = S(a,b) есть ф-я 2-х переем-х a и b, а  и
и  - пост числа, полученные экспериментально.
- пост числа, полученные экспериментально.
Т. о., достаточно исслед-ть ф-ю S = S(a,b) на экстремумах. Находим частные производные
 или
или 


После преобразований, система принимает вид:
(**) 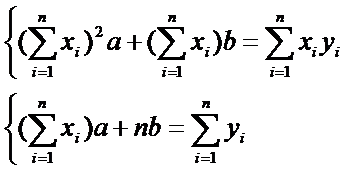 Система (**) - система норм уравнений
Система (**) - система норм уравнений  т.к квадрат ∑ >∑-мы квадратов
т.к квадрат ∑ >∑-мы квадратов 
Ф-я S = S(a,b) достигает своего min при a и b, найд из сист (**). Для этого проверим достаточные условия экстремума: 
 функция достигает min (глобальный min).
функция достигает min (глобальный min).
6. Неопред интеграл, первообразная и их св-ва.
Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x? (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b). Т.: Если F(x) первооб-я ф-и f(x), то F(x)+С тоже пер-я. О. Мн-во всех перв-х ф-й F(x)+С для данной ф-и f(x) наз. неопред интегр ф-и f(x) обозн-ся

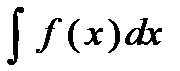
Св-ва НИ:

7. Интегрир-е путем замены переменной (подстановкой)
М-д подстановки

 ∫f(x)dx= [x=φ(t),t=ψ(x),dx=φ’(t)dt] =∫f(φ(t)φ’(t)dt
∫f(x)dx= [x=φ(t),t=ψ(x),dx=φ’(t)dt] =∫f(φ(t)φ’(t)dt
Если интеграл непосредственно не вычисляется,можно применить метод,кот. состоит в след.:
-вводится новая переменная
x=φ(t),где t=ψ(x) явл. обратной по отношению к φ(t), dx=φ’(t)dt- дифференциал ф-ции x=φ(t)
А
7.вычисление площади плоской фигуры заданной системе координат. В полярной системе точка это пара чисел  , любая линия равна
, любая линия равна  .
.


Объемы тел вращения
1. 

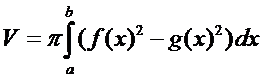
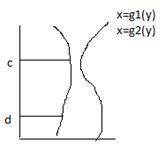
2. 
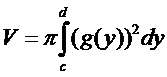
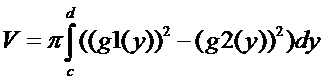
17. Несобственные(н/с) интегралы.
А) н/с интеграл с бесконечным верхним пределом инт.
О1. У=f(x), хЄ[a;+¥), где а- конечное число. Ф-ция f(x) и интегрируема на любом отрезке [а;B] Ì [a;+¥). (1) 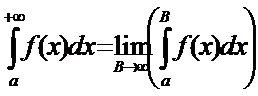 --н/с интеграл с бесконечным верхним пределом
--н/с интеграл с бесконечным верхним пределом
Б) н/с интеграл с бесконечным нижним пределом
О3. у= f(x) (-∞;b), которая определена и интегрируемана [А;В]с(-∞;b)
(2) 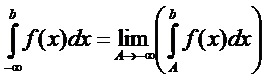 --н/с интеграл с бесконечным нижним пр.
--н/с интеграл с бесконечным нижним пр.
В) н/с интеграл с двумя бесконечн. пределами интегр.
О5. у=f(x) (-∞;+∞), (А;В)с(-∞;+∞)
(3)  --н/с интеграл с 2мя бесконечн пределами можно переписать как
--н/с интеграл с 2мя бесконечн пределами можно переписать как
(4) 
 где -∞<С<+∞, (3)=(4)
где -∞<С<+∞, (3)=(4)
И. на конечном промежутке
А)пусть ф-ция f(x) определена на конечном промежутке [a,b) и интегрируема на любом отрезке [a,x]Ì[a,b)
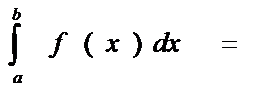
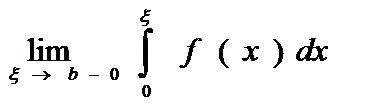
Б)н/с интеграл от разрывных функции
пусть задана ф-ция у=f(x) [a;b], причем cÎ[a;b], такая, что ф-ции f(x) в этой точке имеет бесконечный разрыв (x=c – точка разрыва второго рода), тогда 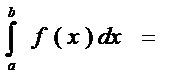
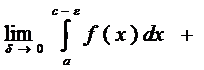
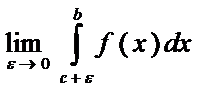 --н/с интеграл от разрывной ф-ции
--н/с интеграл от разрывной ф-ции
Если оба предела в правой части существуют и явл конечными числами, то н/с интеграл разрывн ф-ции назыв сходящимся, а если один из пределов не сущ. или =∞, то н/с интеграл наз. расходящимся
18. Несобственные интегралы от неограниченных ф-й.
Пусть ф-ция определена и интегрируема на замкнутом промежутке [a;b], за исключением конечного числа точек 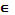 [a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:
[a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:

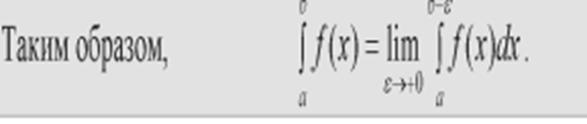
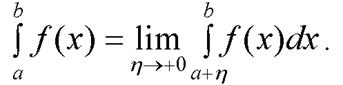

19. Дифференциальное уравнение(ДУ)
Осн.понятия
Реш с помощью подстановки
z=y/x y=zx y’=z’xx+z
z’x+z=g(z) d(z)/(g(z)-z)=d(x)/x
6) y’=f(ax+by) приводится к ур-ю вида (4) путем замены z=ax+by
21. Линейные ДУ 1-го порядка
Уравнение вида  ,
,
где p(x) и q(x) – заданные функции, назыв. линейным дифференциальным уравнением 1-го порядка. Если в ур-нии 1 правая часть тождественно равна 0, то получим ур-ние вида 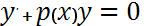 (2) (однородное линейное ДУ 1-го порядка)
(2) (однородное линейное ДУ 1-го порядка)
2—решают как ур-ние с раздел. переменными
1—решают с помощью подстановки:
 ,
, 
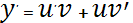
(u’v+uv’)+p(x)uv=q(x)
u’v+u(v’+p(x)v)=q(x)


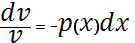
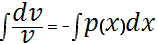
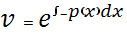
Подставляем во 2-ое уравнение системы (b):
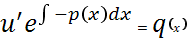

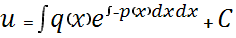
Общее решение уравнения: 
22. Линейные ДУ 2-го порядка.
Вид:

Методика решения:
Уравнение 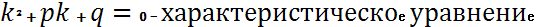
Общее решение зависит от корней характеристического.
a) D<0,  , тогда решение имеет вид:
, тогда решение имеет вид:

b)D=0,  =>
=>

c) D<0, 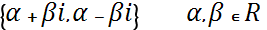 =>
=> 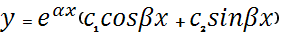
23. Линейные однородные ДУ 2 порядка с постоянными коэфф-ми. Их нахождение.
Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:
(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция
Если r(x) =0, то
(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.
Ур-е вида (3)  =0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)
=0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)
Возможны 3 случая
1. кв.ур-е имеет разные корни α1  α2, D>0 тогда общее решение:
α2, D>0 тогда общее решение:
y=C1  C1, C2 прин.R
C1, C2 прин.R
2. корни кв.ур. кратные, т.е. α1= α2=α; D=0
y=  C1, C2 прин.R
C1, C2 прин.R
3. корни комплексно сопряженные: λ1= α-βi; λ2= α+βi;
y= C1  C1, C2 прин.R
C1, C2 прин.R
24. Лин неоднор ДУ 2-го порядка с пост коэфф-ми.
Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q? R, r(x)-функция. которое имеет вид y=yO+yЧ, где
yO-общее решение уравнения y´´+py´+qy =0
yЧ-частное решение уравнения y´´+py´+qy=r(x), которое зависит от вида правой части,т.е r(x)
Рассмотрим некоторые частные случаи:
1) r(x)=Pn(x),где Pn(x) – многочлен степени «n»
В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде:
• yЧ=Qn(x) при q≠0
• yЧ=x Qn(x) q=0, p≠0
• yЧ=x² Qn(x) q=p=0
2) r(x)=а 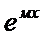 где а,м? R, а,м =соnst
где а,м? R, а,м =соnst
Вид частного решения следущее:
• yЧ=А  если «м» не явл корнем Ур-я к²+pк+q=0
если «м» не явл корнем Ур-я к²+pк+q=0
(корни некратные,некомплексные)
• yЧ=Аx  если «м» –простой корень ур-я к²+pк+q=0
если «м» –простой корень ур-я к²+pк+q=0
•yЧ=Аx² 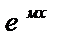 если «м»-кратный корень Ур-я к²+pк+q=0
если «м»-кратный корень Ур-я к²+pк+q=0
3) r(x)=acosmx+bsinmx где a,b,m=const
• yЧ= Acosmx+Bsinmx при условии что p²+(q-m²)≠0
• yЧ= x(Acosmx+Bsinmx) если p²+(q-m²)=0, p=0,q= m²
25. Числовой ряд и его сходимость.
Пусть задана бескон послед-ть чисел 
 …
… 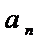
Тогда  +
+ 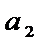 +…
+…  +…=
+…= 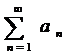 (1) наз числовым рядом, а числа
(1) наз числовым рядом, а числа 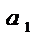
 -члены ряда,
-члены ряда,  -общий член ряда.
-общий член ряда.
Сумма ряда. Примеры сходящихся и расходящихся рядов. Гармонический ряд (док-во его расходимости).
Сумма вида  =
= 
 =
=  +
+ 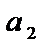 =
=  +
+ 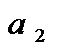
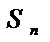 =
=  +
+  +…
+… 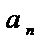 =
= 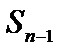 +
+ 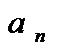
Свойства сходящихся рядов
Свойства- 1. Если ряд u1+u2+u3+….un+…=  (1) сход(расх.). И его сумма-S то сход(расх если с не равно 0),также и ряд
(1) сход(расх.). И его сумма-S то сход(расх если с не равно 0),также и ряд  и его сумма c*S.
и его сумма c*S.
2. Если ряд (1) и ряд  их суммы S1 и S2 соответственно,то сход и ряды
их суммы S1 и S2 соответственно,то сход и ряды  и их суммы равны S1+S2.
и их суммы равны S1+S2.
3. Если к ряду (1) прибавить или отнять от него конечное число членов, то получим ряд и ряд (1) сход или расх одновременно. Ряд un+1+un+2+…=  обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем. к 0 при n стрем. к бесконечн.(
обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем. к 0 при n стрем. к бесконечн.( Rn=0).
Rn=0).
Необход.признак сходимости - если ряд(1) сход. то общий член этого ряда стрем к 0 ( an=0) Док-во:
an=0) Док-во:  un=
un=  (Sn-Sn-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но un= 1/n стрем. к 0).
(Sn-Sn-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но un= 1/n стрем. к 0).
Док-во расх-ти гармонического ряда по Коши: f(x)=1/x  =
= 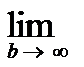 ;
; 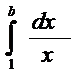 =
=  (lnx)
(lnx)  =
=  (lnB*0),где lnB→
(lnB*0),где lnB→ 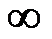
Ряд  гармонический и он всегда расход
гармонический и он всегда расход
Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q.
Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:

Степенной ряд можно почленно интегрировать на любом отрезке, целиком принадлежащем интервалу сходимости. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз. Ряды, полученные почленным интегрированием и почленным дифференцированием степенного ряда, имеют тот же радиус сходимости, что и исх ряд.
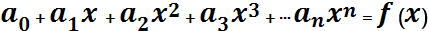 , область сход-ти (-R;R). Тогда для x
, область сход-ти (-R;R). Тогда для x 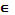 (-R;R) ряд f(x) можно почленно дифференцировать. Также его можно почленно интегрировать для всех x
(-R;R) ряд f(x) можно почленно дифференцировать. Также его можно почленно интегрировать для всех x 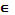 (a,b)<(-R;R).
(a,b)<(-R;R). 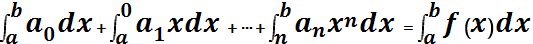 .
.
35. Разложение некоторых элементарных ф-ций в степенные ряды
Х – обл-ть опред-я ф-ции
х1, х2… хn – независ-е переем-е (аргументы)
Z – ф-ция Пример: Z=П х21*х2 (Объем цилиндра)
Рассм-м Z=f(х;у) – ф-цию 2-х перем-х (х1, х2 замен-ся на х,у). Рез-ты по аналогии переносятся на др. ф-ции многих перем-х. Обл-ть опред-я ф-ции 2-х перем-х – вся корд пл-ть (оху) или ее часть. Мн-во знач-й ф-ции 2-х перем-х – поверх-ть в 3х-мерном простр-ве.
Приемы построения графиков: - Рассм-т сечение поверх-ти пл-тями || координатным пл-тям.
Пример: х = х0, зн. пл-ть Х || 0уz у = у0 0хz Вид ф-ции: Z=f(х0,y); Z=f(x,у0)
Например: Z=x2+y2-2y
Z= x2+(y-1)2-1 x=0 Z=(y-1)2-1 y=1 Z= x2-1 Z=0 x2+(y-1)2-1
Парабола окруж-ть(центр(0;1)
1б .Пределы и непрерывность ф-ций двух переменных
Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.(х0,y0), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,у удовл-щих |x-х0|<б; |y-y0|<б выполняется нерав-во |f(x,y)-A|<E
Z=f(х;у) непрерывна в т.(х0,y0), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х0 и у к у0; - этот предел = знач-ю
ф-ции в т.(х0,y0), т.е. limf(х;у)=f(х0,y0)




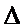 х,
х,  z = f(x+
z = f(x+ 
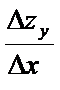
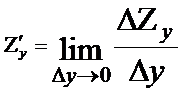 Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.
Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.
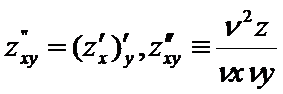
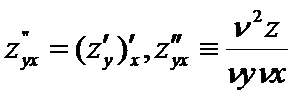
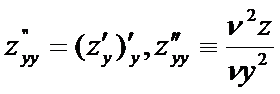
 - наз полным дифференциалом
- наз полным дифференциалом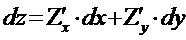
 наз max(min) ф-и z = f(x,y), если сущ некот окрест-ть т.
наз max(min) ф-и z = f(x,y), если сущ некот окрест-ть т. 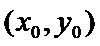 такая, что для всех x,y из этой окрест-ти вып-ся нер-во f(x,y)<f
такая, что для всех x,y из этой окрест-ти вып-ся нер-во f(x,y)<f 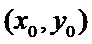 (max) или f(x,y)>f
(max) или f(x,y)>f  (min). Т.: Если задана точка экс-ма ф-и 2-х переем-х, то знач-е частных произв-х в этой точке = 0, т.е.
(min). Т.: Если задана точка экс-ма ф-и 2-х переем-х, то знач-е частных произв-х в этой точке = 0, т.е. 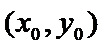 ,
, 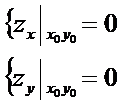
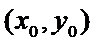 , в которых частные производные первого порядка называются стационарными или критическими.
, в которых частные производные первого порядка называются стационарными или критическими.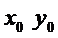 стационарная точка,
стационарная точка,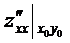 , B =
, B =  , C =
, C =  ,
,  , тогда
, тогда , причем max, если A<0, min, если A>0.
, причем max, если A<0, min, если A>0.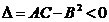 , экстр-ма в т.
, экстр-ма в т. 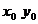 нет
нет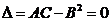 , треб-ся доп исслед-е
, треб-ся доп исслед-е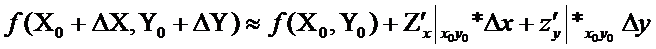
 ) была мин. Невязка (
) была мин. Невязка ( ) – это –откл-е от «теоретич» знач-й
) – это –откл-е от «теоретич» знач-й  , найд по эмпирич формулам y = f(x) от соответствующих опытных знач-й
, найд по эмпирич формулам y = f(x) от соответствующих опытных знач-й  . Рассм-м функцию
. Рассм-м функцию  (т.е. сумму квадратов всех невязок) Пусть в кач-ве ф-и у = f(x) взята лин ф-я у = ax + b. Тогда задание сводится к отыскиванию пар-ов a и b, при кот ф-я
(т.е. сумму квадратов всех невязок) Пусть в кач-ве ф-и у = f(x) взята лин ф-я у = ax + b. Тогда задание сводится к отыскиванию пар-ов a и b, при кот ф-я  принимает наим зн-е. Очевидно, что S = S(a,b) есть ф-я 2-х переем-х a и b, а
принимает наим зн-е. Очевидно, что S = S(a,b) есть ф-я 2-х переем-х a и b, а  и
и  - пост числа, полученные экспериментально.
- пост числа, полученные экспериментально. или
или 


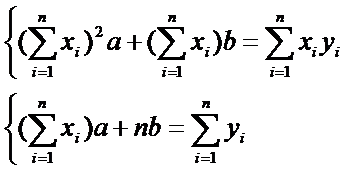 Система (**) - система норм уравнений
Система (**) - система норм уравнений  т.к квадрат ∑ >∑-мы квадратов
т.к квадрат ∑ >∑-мы квадратов 

 функция достигает min (глобальный min).
функция достигает min (глобальный min).
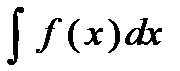


 , любая линия равна
, любая линия равна  .
.



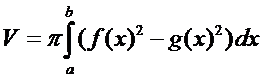

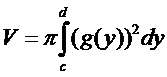
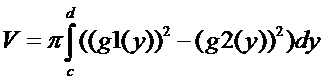
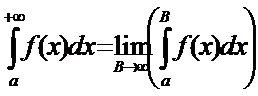 --н/с интеграл с бесконечным верхним пределом
--н/с интеграл с бесконечным верхним пределом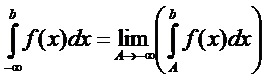 --н/с интеграл с бесконечным нижним пр.
--н/с интеграл с бесконечным нижним пр. --н/с интеграл с 2мя бесконечн пределами можно переписать как
--н/с интеграл с 2мя бесконечн пределами можно переписать как
 где -∞<С<+∞, (3)=(4)
где -∞<С<+∞, (3)=(4)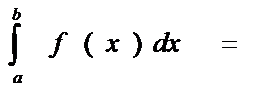
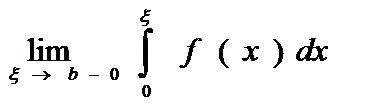
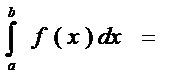
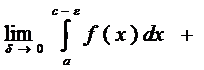
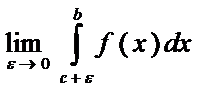 --н/с интеграл от разрывной ф-ции
--н/с интеграл от разрывной ф-ции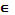 [a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:
[a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:
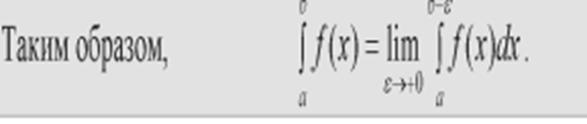
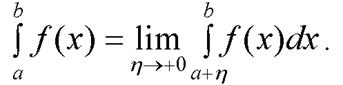

 ,
,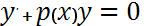 (2) (однородное линейное ДУ 1-го порядка)
(2) (однородное линейное ДУ 1-го порядка) ,
, 
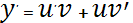


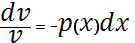
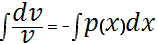
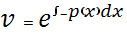
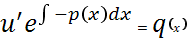

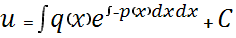


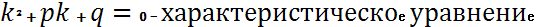
 , тогда решение имеет вид:
, тогда решение имеет вид:
 =>
=>
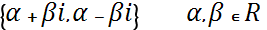 =>
=> 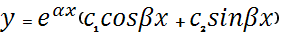
 =0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)
=0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3) α2, D>0 тогда общее решение:
α2, D>0 тогда общее решение: C1, C2 прин.R
C1, C2 прин.R C1, C2 прин.R
C1, C2 прин.R C1, C2 прин.R
C1, C2 прин.R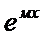 где а,м? R, а,м =соnst
где а,м? R, а,м =соnst если «м» не явл корнем Ур-я к²+pк+q=0
если «м» не явл корнем Ур-я к²+pк+q=0 если «м» –простой корень ур-я к²+pк+q=0
если «м» –простой корень ур-я к²+pк+q=0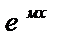 если «м»-кратный корень Ур-я к²+pк+q=0
если «м»-кратный корень Ур-я к²+pк+q=0
 …
… 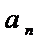
 +
+ 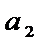 +…
+…  +…=
+…= 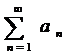 (1) наз числовым рядом, а числа
(1) наз числовым рядом, а числа 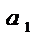
 -члены ряда,
-члены ряда,  -общий член ряда.
-общий член ряда. =
= 
 =
=  +
+ 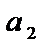 =
=  +
+ 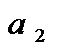
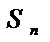 =
=  +…
+… 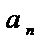 =
= 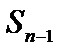 +
+ 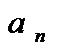
 (1) сход(расх.). И его сумма-S то сход(расх если с не равно 0),также и ряд
(1) сход(расх.). И его сумма-S то сход(расх если с не равно 0),также и ряд  и его сумма c*S.
и его сумма c*S. их суммы S1 и S2 соответственно,то сход и ряды
их суммы S1 и S2 соответственно,то сход и ряды  и их суммы равны S1+S2.
и их суммы равны S1+S2. обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем. к 0 при n стрем. к бесконечн.(
обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем. к 0 при n стрем. к бесконечн.( Rn=0).
Rn=0). an=0) Док-во:
an=0) Док-во:  un=
un=  (Sn-Sn-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но un= 1/n стрем. к 0).
(Sn-Sn-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но un= 1/n стрем. к 0). =
= 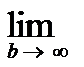 ;
; 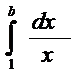 =
=  (lnx)
(lnx)  =
=  (lnB*0),где lnB→
(lnB*0),где lnB→ 
 гармонический и он всегда расход
гармонический и он всегда расход
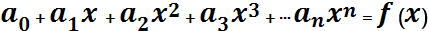 , область сход-ти (-R;R). Тогда для x
, область сход-ти (-R;R). Тогда для x 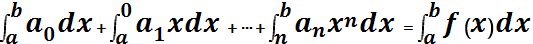 .
. 


