

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|


 x+p/2=t dx=dt a2=
x+p/2=t dx=dt a2= 
 или
или 
IV
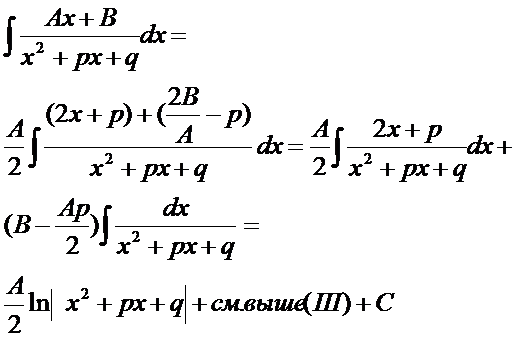
V. 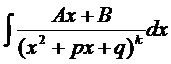
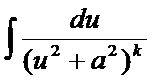 p²/4-q>0
p²/4-q>0
 p²/4-q<0
p²/4-q<0
10. Интегрирование рациональных дробей
1. Многочленом степени n наз-ся выражение вида a0+a1x+a2x2+…+anxn=Pn(x)
Рациональной дробью наз-ют отношение двух многочленов вида  При n=0 вычисление интеграла никаких трудностей не представляет
При n=0 вычисление интеграла никаких трудностей не представляет
Интерес представляют рациональные дроби, у кот. n>0 При этом будем рассматривать дроби, у кот. m<n Если m>=n, то применяют процедуру деления многочленов уголком
Интегрирование простейших дробей





 I.
I. 
 x-a=t dx=dt
x-a=t dx=dt 

 II.
II.  x-a=t dx=dt
x-a=t dx=dt 
11 Определение опред. интеграла
Пусть зад ф у=f(x), кот непрер на некот. замкнутом инт-ле [a,b].
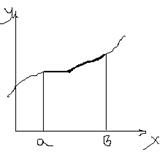 Разбиваем инт-л [a,b] на n частей; абсциссы точек дел-я a=x0<x1<x2<…<xi-1<xn-1<xn=b обозн x1,x2,…xn. Кажд частичный инт-л обозн ∆x1=x1-x0, ∆x2=x2-x1, ∆xi=xi-xi-1, ∆xn=xn-xn-1. В каждом частичном инт-ле ∆xi, i= 1;n выберем т. и выч-м ﻉ I, y=f(x), y=f( ﻉ 1), f( ﻉ 2), … f( ﻉ i),… f( ﻉ n) Cост-м произв-е f( ﻉ 1)∆x1, f( ﻉ 2)∆x2, … f( ﻉ i)∆xi,… f( ﻉ n)∆xn. Кажд из этих произв-й предст собой полоску шириной ∆xi и высотой f( ﻉ i).
Разбиваем инт-л [a,b] на n частей; абсциссы точек дел-я a=x0<x1<x2<…<xi-1<xn-1<xn=b обозн x1,x2,…xn. Кажд частичный инт-л обозн ∆x1=x1-x0, ∆x2=x2-x1, ∆xi=xi-xi-1, ∆xn=xn-xn-1. В каждом частичном инт-ле ∆xi, i= 1;n выберем т. и выч-м ﻉ I, y=f(x), y=f( ﻉ 1), f( ﻉ 2), … f( ﻉ i),… f( ﻉ n) Cост-м произв-е f( ﻉ 1)∆x1, f( ﻉ 2)∆x2, … f( ﻉ i)∆xi,… f( ﻉ n)∆xn. Кажд из этих произв-й предст собой полоску шириной ∆xi и высотой f( ﻉ i).
О1. Сумма f( ﻉ 1)∆x1+ f( ﻉ 2)∆x2 + … f( ﻉ i)∆xi +… f( ﻉ n)∆xn=∑ f( ﻉ 1)∆x1 наз интегр суммой ф. f(x) на инт-ле [a,b]. С геом. точки предст собой S ступенчатой фигуры.
Обозн наиб. из разностей ∆x1= xi-xi-1 через ОХ. Тогда имеет место определение 2.
О2. Сущ кон предел интегр ∑, т.е. 
 f( ﻉ 1)∆x1 и он не зав-т от СП-ба разбиения инт-ла [a,b] и выбора точек ﻉ 1 на частичных инт-лах ∆xi, то этот предел наз опред интегралом ф. f(x) на [a,b] и обозн
f( ﻉ 1)∆x1 и он не зав-т от СП-ба разбиения инт-ла [a,b] и выбора точек ﻉ 1 на частичных инт-лах ∆xi, то этот предел наз опред интегралом ф. f(x) на [a,b] и обозн 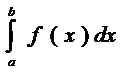
Т. Для всякой непрер ф-и интеграл сущ.
А Геом. смысл опред. интеграла.
Опред интеграл опред-т точное зн-е S криволин тр-и.
12. Осн св-ва опред интеграла
 Значение о.и. не зависит от обозначения переменной интегрирования.
Значение о.и. не зависит от обозначения переменной интегрирования.
|
|

Если  , x? [a;b]
, x? [a;b] 
13. Формула Ньютона-Лейбница (вывод)
Т: Если  непрерывна на
непрерывна на 
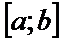 , справедлива ф-ла Ньютона-Лейбница:
, справедлива ф-ла Ньютона-Лейбница: 
Рассм-м  , т.к.
, т.к.  , то
, то  - первообразная для
- первообразная для  . Но
. Но  , также первообразная. Это значит что имеет место следующее равенство:
, также первообразная. Это значит что имеет место следующее равенство: 
 Подставим верхнюю границу:
Подставим верхнюю границу: 
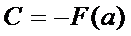 подставами вместо
подставами вместо  :
:  в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования,запишем:
в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования,запишем: 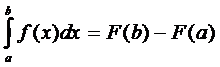
Определенный интеграл с переменным верхним пределом
Ф-я вида  , где x
, где x  наз интегралом c перем верхним пределом. Т: Если
наз интегралом c перем верхним пределом. Т: Если  непрер на
непрер на  , то произв-я ф-и
, то произв-я ф-и  , сущ в каждой точке
, сущ в каждой точке 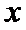 на
на  , причем
, причем 
Интегрирование по частям и замена переменной в определенном интеграле
Формула интегрирования по частям для определенном интеграла.
Пусть заданны  тогда имеет место интегрирование по частям:
тогда имеет место интегрирование по частям:
 →
→ 
Замена переменной в определенном интеграле.
Пусть  непрерывна на
непрерывна на  , а
, а 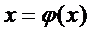 непрерывна на
непрерывна на  . Вместе со своей производной
. Вместе со своей производной  ; причем
; причем  , и сложная функция
, и сложная функция  непрерывна на
непрерывна на  , тогда справедливо формула замены переменной для определенного интеграла:
, тогда справедливо формула замены переменной для определенного интеграла:
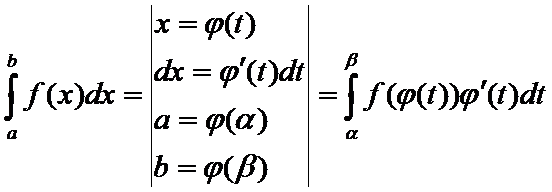
Геометрич приложения определенного интеграла
Вычисление площадей плоских фигур:
 1.
1. 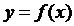 на
на 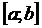 и
и 

2.  на
на 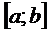 и
и 


 3.
3.  на
на 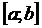 график имеет вид
график имеет вид


 4. даны две функции:
4. даны две функции:  и
и  на промежутке
на промежутке 


 5.
5.  на промежутке
на промежутке  то получаем
то получаем 
 6.
6.  и
и  на промежутке
на промежутке  (графики ориентированны на
(графики ориентированны на  )
) 
А
7.вычисление площади плоской фигуры заданной системе координат. В полярной системе точка это пара чисел  , любая линия равна
, любая линия равна  .
.


|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!