 Пусть
Пусть 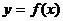 - дифференцируемая на интервале - дифференцируемая на интервале 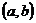 функция.
Определение 1. Функция функция.
Определение 1. Функция  возрастает на возрастает на  тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
Определение 2. Функция тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
Определение 2. Функция 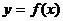 убывает на убывает на 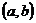 тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка. тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
| f(x)ä
| 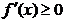
| | f(x) æ
| 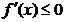
| Определение 3. Критическими точками функции (первого рода) называются точки, в которых производная функции равна нулю или не существует.
Определение 4. Пусть функция 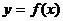 непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда: непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда:
1. если производная 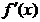 при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума; при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
2. если производная 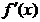 при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума. при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума.
| хо – критическая точка: f`(xо) =0 или f`(xо) не существует
| | хо – точка минимума
|   хо хо
|  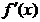 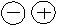
| | хо – точка максимума
|  хо
хо
| 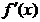 
|
Для нахождения промежутков монотонности и точек экстремума функции используется следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции.
3. Определите критические точки первого рода (f'(xo) =0 или f'(xo) не существует).
4.На числовой оси отметьте критические точки и определите знаки производной на каждом из получившихся интервалов. (подставить удобное число в производную и вычислить).
5.Выпишите интервалы монотонности. Выпишите точки экстремума функции (если они есть), используя соответствующие критерии, вычислите значения функции в точках экстремума.
Пример 1. Найдите промежутки монотонности и точки экстремума функции 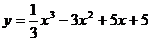 . .
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции: 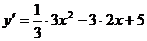 = = 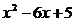 . .
3. Определим критические точки первого рода (у' =0): 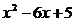 =0; =0;
х 1=1 или х 2=5.
4. На числовой оси отметим критические точки х 1=1 и х 2=5. Эти точки разбивают область определения функции на три интервала (-∞;1), (1;5); (5;+∞). Расставим знаки производной функции у' = 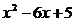 на каждом из полученных интервалов: на каждом из полученных интервалов:
при х =0  (-∞;1) у' (0)=5>0; (-∞;1) у' (0)=5>0;
при х =2  (1;5) у' (2)= (1;5) у' (2)= 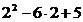 =-3<0; =-3<0;
при х =6  (5;+∞) у' (6)= (5;+∞) у' (6)= 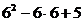 =5>0. =5>0.
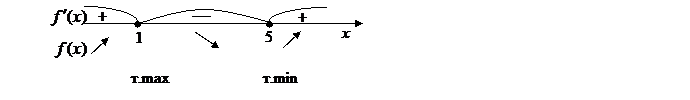
5. Согласно критерию возрастания и убывания функция 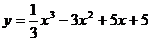 возрастает при х возрастает при х 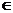 (-∞;1] (-∞;1] 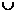 [5;+∞), убывает при х [5;+∞), убывает при х 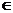 [1;5]. [1;5].
Согласно критерию нахождения точек экстремума х =1 – точка максимума, х =5 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
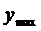 = = 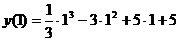 = = 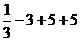 = = 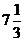 - максимум функции; - максимум функции;
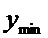 = = 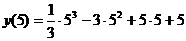 = = 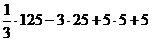 = = 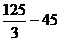 = = 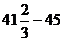 = = 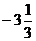 - минимум функции. - минимум функции.
Ответ: 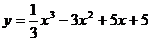 возрастает при х возрастает при х  (-∞;1] (-∞;1] 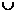 [5;+∞), убывает при х [5;+∞), убывает при х  [1;5]. х =1 – точка максимума; [1;5]. х =1 – точка максимума; 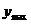 = = 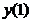 = = 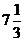 ; х =5 – точка минимума; ; х =5 – точка минимума;  = =  = = 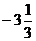 . .
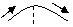
Определение 5. График функции 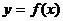 называется вогнутым на интервале называется вогнутым на интервале 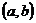 , если он расположен выше любой касательной к графику функции на данном интервале. , если он расположен выше любой касательной к графику функции на данном интервале.
Определение 6. График функции 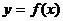 называется выпуклым на интервале называется выпуклым на интервале 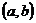 , если он расположен ниже любой касательной к графику функции на данном интервале. , если он расположен ниже любой касательной к графику функции на данном интервале.
Определение 7. Точка графика непрерывной функции, в которой меняется характер выпуклости, называется точкой перегиба.
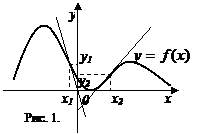 Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости. Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.
Так, график функции на рис.1. является выпуклым на промежутках (-  ; х 1) и (х 2; + ; х 1) и (х 2; +  ); вогнутым на (х 1; х 2). График функции имеет две точки перегиба: (х 1; у 1) и (х 2; у 2). ); вогнутым на (х 1; х 2). График функции имеет две точки перегиба: (х 1; у 1) и (х 2; у 2).
Критерий выпуклости-вогнутости функции: если функция 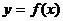 имеет положительную вторую производную, то график функции на интервале имеет положительную вторую производную, то график функции на интервале 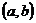 вогнутый; вогнутый;
если функция 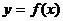 имеет отрицательную вторую производную, то график функции на интервале имеет отрицательную вторую производную, то график функции на интервале 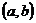 выпуклый. выпуклый.
| f(x) вогнутая
| 
| 
| | f(x) выпуклая
| 
| 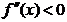
| Таким образом, исследовать функцию на выпуклость-вогнутость означает найти те интервалы области определения, в которых вторая производная сохраняет свой знак.
Определение 8. Критическими точками функции второго р ода называются те точки, в которых вторая производная равна нулю или не существует.
Только критические точки могут быть точками перегиба. Для их нахождения используется следующая теорема:
Теорема (достаточное условие существования точек перегиба). Если вторая производная 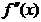 при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба. при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.
При исследовании функции 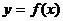 на выпуклость-вогнутость и точки перегиба удобно использовать следующий алгоритм: на выпуклость-вогнутость и точки перегиба удобно использовать следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции 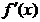 . .
3. Найдите вторую производную функции 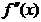 . .
4. Определите критические точки второго рода (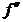 (xo) =0 или (xo) =0 или 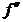 (xo) не существует). (xo) не существует).
5. На числовой оси отметьте критические точки второго рода и определите знаки второй производной на каждом из получившихся интервалов.(подставить удобное число во вторую производную и вычислить)
6. Найдите интервалы выпуклости-вогнутости графика функции, используя соответствующие критерии; выпишите абсциссы точек перегиба (если они есть) и найдите значение функции в этих точках.
Пример 2. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 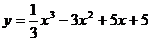 . .
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции: 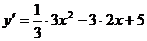 = = 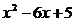 . .
3. Найдем вторую производную функции: 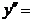 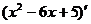 =2 х -6. =2 х -6.
4. Определим критические точки второго рода (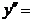 0): 2 х -6= 0 0): 2 х -6= 0 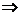 х =3. х =3.
5. На числовой оси отметим критическую точку х =3. Она разбивает область определения функции на два интервала (-∞;3) и (3;+∞). Расставим знаки второй производной функции 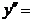 2 х -6 на каждом из полученных интервалов: 2 х -6 на каждом из полученных интервалов:
при х =0 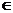 (-∞;3) (-∞;3) 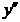 (0)=-6<0; (0)=-6<0;
при х =4 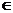 (3;+∞) (3;+∞) 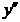 (4)= 2∙4-6=2>0. (4)= 2∙4-6=2>0.

6. Согласно критерию выпуклости-вогнутости график функции 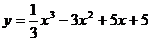 выпуклый при х выпуклый при х 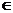 (-∞;3), вогнутый при х (-∞;3), вогнутый при х 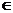 (3;+ ∞). (3;+ ∞).
Значение х =3 – абсцисса точки перегиба. Вычислим значение функции при х =3:
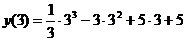 = = 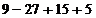 =2. Итак, точка с координатами (3;2) – точка перегиба. =2. Итак, точка с координатами (3;2) – точка перегиба.
Ответ: график функции 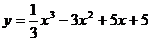 выпуклый при х выпуклый при х  (-∞;3), (-∞;3),
вогнутый при х  (3;+ ∞); (3;2) – точка перегиба. (3;+ ∞); (3;2) – точка перегиба.
Пример 3. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 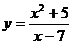 . .
Решение. 1. Данная функция определена в том случае, когда знаменатель отличен от нуля: х -7≠0 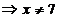 . .
2. Найдем первую производную функции:
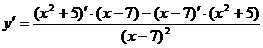 = = 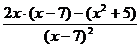 = = 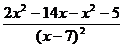 = =
= 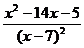 . .
3. Найдем вторую производную функции: 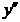 = = 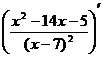 = =
= 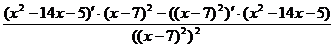 = =
= 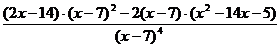 . .
Вынесем в числителе 2∙(х -7) за скобки:
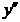 = = 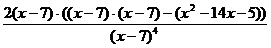 =2∙ =2∙ 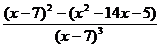 = =
= 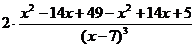 = = 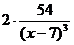 = = 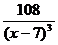 . .
4. Определим критические точки второго рода: 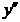 не может быть равна нулю, поскольку числитель дроби 108≠0. не может быть равна нулю, поскольку числитель дроби 108≠0.
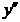 не существует, если (х -7)3=0 не существует, если (х -7)3=0 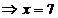 - критическая точка второго рода. - критическая точка второго рода.
5. На числовой оси отметим критическую точку х =7 выколотой точкой, поскольку в этой точке функция 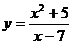 не определена. Эта точка разбивает область определения функции на два интервала (-∞;7) и (7;+∞). Расставим знаки второй производной функции не определена. Эта точка разбивает область определения функции на два интервала (-∞;7) и (7;+∞). Расставим знаки второй производной функции 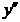 = = 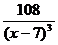 на каждом из полученных интервалов: на каждом из полученных интервалов:
при х =6  (-∞;7) (-∞;7)  (6)= (6)= 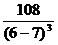 <0; <0;
при х =8 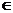 (7;+∞) (7;+∞) 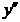 (8)= (8)= 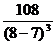 >0. >0.

6. Согласно критерию выпуклости-вогнутости график функции 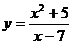 является выпуклым при х является выпуклым при х 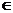 (-∞;7), вогнутым при х (-∞;7), вогнутым при х 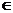 (7;+ ∞). (7;+ ∞).
Точка с абсциссой х =7 не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
Ответ: график функции 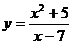 выпуклый при х выпуклый при х 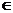 (-∞;7), (-∞;7),
вогнутый при х 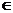 (7;+ ∞). (7;+ ∞).
| 


 Пусть
Пусть 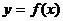 - дифференцируемая на интервале
- дифференцируемая на интервале 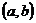 функция.
Определение 1. Функция
функция.
Определение 1. Функция 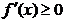
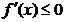
 при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
 хо
хо

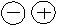
 хо
хо
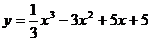 .
.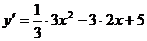 =
= 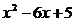 .
.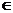 (-∞;1) у' (0)=5>0;
(-∞;1) у' (0)=5>0;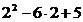 =-3<0;
=-3<0;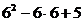 =5>0.
=5>0.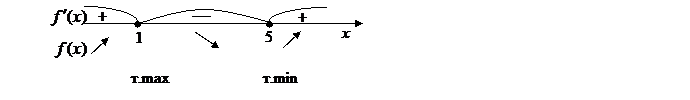
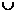 [5;+∞), убывает при х
[5;+∞), убывает при х 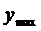 =
= 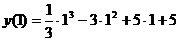 =
= 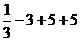 =
= 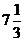 - максимум функции;
- максимум функции; =
= 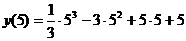 =
= 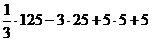 =
= 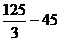 =
= 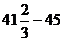 =
= 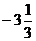 - минимум функции.
- минимум функции.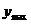 =
= 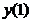 =
= 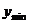 =
= 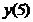 =
= 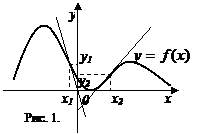 Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.
Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.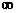 ; х 1) и (х 2; +
; х 1) и (х 2; + 

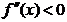
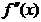 при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.
при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.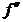 (xo) =0 или
(xo) =0 или 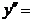
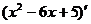 =2 х -6.
=2 х -6.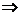 х =3.
х =3.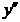 (0)=-6<0;
(0)=-6<0;
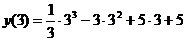 =
= 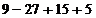 =2. Итак, точка с координатами (3;2) – точка перегиба.
=2. Итак, точка с координатами (3;2) – точка перегиба.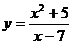 .
.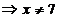 .
.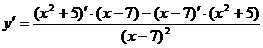 =
= 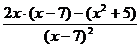 =
= 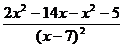 =
=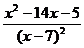 .
.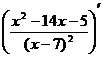 =
=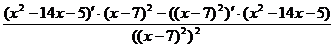 =
=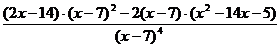 .
.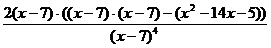 =2∙
=2∙ 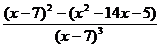 =
=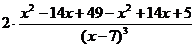 =
= 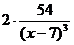 =
= 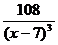 .
.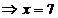 - критическая точка второго рода.
- критическая точка второго рода.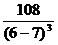 <0;
<0;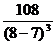 >0.
>0.

