Решение задачи о нахождении площади плоской фигуры или объема пространственной фигуры, прежде всего, площади простого многоугольника или объема простого многогранника, осуществляется: либо разбиением данной фигуры на составляющие фигуры, площади или объемы которых мы уже умеем находить, либо её дополнением известными в этом смысле фигурами до фигуры, площадь или объем которой нам уже известен. Часто эти приемы применяются одновременно (рис. 99).

Рис.99
«Отрезаем» треугольник 
 и «добавляем его» к параллелограмму, получаем прямоугольник
и «добавляем его» к параллелограмму, получаем прямоугольник  , площадь которого есть сумма площадей двух фигур, из которых состоит параллелограмм
, площадь которого есть сумма площадей двух фигур, из которых состоит параллелограмм  . На этом основании заключаем, что площадь параллелограмма равна площади прямоугольника.
. На этом основании заключаем, что площадь параллелограмма равна площади прямоугольника.
Другой пример представлен на рисунке 100. «Крест» составленный из пяти одинаковых квадратов, преобразуется в квадрат путем «обрезания» четырех прямоугольных треугольников (заштрихованы на рисунке) и добавления их к оставшейся от креста фигуре так, как показано на рисунке. Площадь «креста» равна площади полученного квадрата.

Рис.100
Еще один пример этого рода, на рисунке 101 показан способ определения площади треугольника. MN – средняя линия, 
 .
.

Рис. 101
Параллелограмм BMPC имеет площадь, равную площади 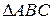 .
.
Можно указать общий прием преобразования простого многоугольника в равный ему по площади треугольник (рис. 102).

Рис. 102
Выбираются три последовательные вершины, например, A 1 , A 2 , A 3. Через A 2 проводится прямая, параллельная диагонали A 1 A 3 и отмечается точка ее пересечения с прямой A 1 A 4 (в общем случае – с прямой A 1 A n). В результате фигура 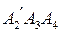 (в общем случае
(в общем случае  ) имеет площадь равную площади исходного многоугольника. Следует, однако, заметить разницу с предыдущими случаями перестроения данной фигуры, которая состоит в том, что данная фигура и построенная, строго говоря, имеют равные площади не потому, что составлены из попарно равных фигур, а потому, что одна, или несколько, как в правой части рисунка, пар треугольников – треугольники, имеющие равные площади, хотя они и не равны друг другу.
) имеет площадь равную площади исходного многоугольника. Следует, однако, заметить разницу с предыдущими случаями перестроения данной фигуры, которая состоит в том, что данная фигура и построенная, строго говоря, имеют равные площади не потому, что составлены из попарно равных фигур, а потому, что одна, или несколько, как в правой части рисунка, пар треугольников – треугольники, имеющие равные площади, хотя они и не равны друг другу.
Как видим, приемы нахождения площади, связанные с заменой одной фигуры другой, равной ей по площади, приводят нас к необходимости, с одной стороны, введения специальных (новых) понятий равносоставленности и равновеликости фигур, а затем требуют и решения вопроса о взаимосвязи этих понятий. Такую же ситуацию мы имеем и в случае перехода к пространственным фигурам.
1. Две фигуры называют равносоставленными, если их можно разбить на одинаковое число попарно равных фигур. Обратим внимание на то, что речь идет о равенстве фигур, являющихся элементами разбиений разных фигур. На рисунках 99, 100, 101 мы имеем примеры равносоставленных фигур.
Когда речь идет о равносоставленных многоугольниках или многогранниках, то их разбивают на попарно равные треугольники или, соответственно, тетраэдры (треугольные пирамиды).
2. Две фигуры называются равновеликими, если равны их площади или объемы, в зависимости от того, являются ли рассматриваемые фигуры плоскими или пространственными.
В этой лекции мы рассматриваем соотношения между этими понятиями.
1  . Равновеликость и равносоставленность многоугольников.
. Равновеликость и равносоставленность многоугольников.
Здесь речь идет о простых многоугольниках, хотя на рисунках будут фигурировать только выпуклые многоугольники. Очевидно, что два равносоставленных многоугольника равновелики. Возникает естественный вопрос о обратном переходе: будут ли равновеликие многоугольники равносоставленными? Ответ на этот вопрос был дан в первой половине XIX века независимо друг от друга венгерским математиком Фаркашем Бойяи (1832 г.) и немецким офицером любителем математики Гервином (1833 г.). Доказательством теоремы Бойаи-Гервина мы и займемся сейчас.
Лемма 1. Если два параллелограмма имеют две равные стороны и равные высоты, опущенные на равные стороны, то они равносоставлены.
Используем как факт то, что отношение равносоставленности является отношением эквивалентности. Существует прямоугольник равносоставленный с каждым из данных параллелограммов (см. рис. 99 и текст к нему). Значит, по транзитивности отношения равносоставленности будут равносоставлены и данные параллелограммы.
Лемма 2. Треугольник равносоставлен с параллелограммом, имеющим сторону, равную стороне треугольника и высоту в два раза меньшую соответствующей высоты треугольника.
Обратимся к рис. 101. На нем имеем 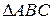 и параллелограмм
и параллелограмм  , находящиеся в условиях леммы. Равносоставленность этих фигур видна из рисунка.
, находящиеся в условиях леммы. Равносоставленность этих фигур видна из рисунка.
Лемма 3. Треугольники с равными основаниями и равными высотами равносоставлены.
От данных треугольников 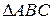 и
и 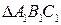 с равными основаниями BC и B 1 C 1 и равными высотами, опущенными из A и A 1 соответственно на BC и B 1 C 1, переходим к параллелограммам с равными сторонами и равными высотами, которые равносоставлены по лемме 1. Каждый из них равносоставлен с треугольниками
с равными основаниями BC и B 1 C 1 и равными высотами, опущенными из A и A 1 соответственно на BC и B 1 C 1, переходим к параллелограммам с равными сторонами и равными высотами, которые равносоставлены по лемме 1. Каждый из них равносоставлен с треугольниками 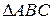 и
и 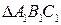 по лемме 2. Тогда в силу транзитивности отношения равносоставленности равносоставлены и треугольники
по лемме 2. Тогда в силу транзитивности отношения равносоставленности равносоставлены и треугольники  и
и  .
.
Лемма 4. Два равновеликих треугольника с равными основаниями имеют и равные высоты (соответствующие этим основаниям).
Пусть 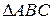 равновелик
равновелик  и при этом
и при этом  (рис. 103).
(рис. 103).

Рис. 103
Последовательно переходим от 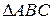 к параллелограмму
к параллелограмму  , а от
, а от  к параллелограмму
к параллелограмму  . Последние равновелики друг другу по транзитивности. Затем от параллелограмма
. Последние равновелики друг другу по транзитивности. Затем от параллелограмма  – к прямоугольнику
– к прямоугольнику  ,а от параллелограмма
,а от параллелограмма  – к прямоугольнику
– к прямоугольнику  . Прямоугольники так же равновелики. Так у этих прямоугольников по условию
. Прямоугольники так же равновелики. Так у этих прямоугольников по условию  , то их стороны A2B и
, то их стороны A2B и  равны в силу известного выражения площади прямоугольника в виде произведения его смежных сторон (см. лекцию 5, пункт
равны в силу известного выражения площади прямоугольника в виде произведения его смежных сторон (см. лекцию 5, пункт  ). Но A2B и
). Но A2B и  – высоты треугольников
– высоты треугольников 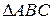 и
и  .
.
Лемма 5. Равновеликие треугольники равносоставлены.
Пусть 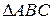 равновелик
равновелик  . Для определенности положим, что
. Для определенности положим, что 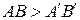 (рис. 104).
(рис. 104).

Рис.104
Через  проводим прямую l параллельно
проводим прямую l параллельно  и, построив окружность
и, построив окружность  , отмечаем точку A 1 пересечения l с окружностью
, отмечаем точку A 1 пересечения l с окружностью  . В силу леммы 3
. В силу леммы 3  равносоставлен с
равносоставлен с  . С другой стороны, в силу равносоставленности
. С другой стороны, в силу равносоставленности  равновелик
равновелик  , а значит равновелик и треугольнику ABC. Треугольники
, а значит равновелик и треугольнику ABC. Треугольники 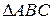 и
и  имеют при этом равные стороны AB и
имеют при этом равные стороны AB и  . По этой причине в силу леммы 4
. По этой причине в силу леммы 4 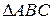 и
и  имеют и равные высоты, проведенные в них из вершин C и
имеют и равные высоты, проведенные в них из вершин C и  . Тогда по лемме 3 эти треугольники (т. е.
. Тогда по лемме 3 эти треугольники (т. е. 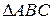 и
и  ) равносоставлены. По транзитивности отношения равносоставленности
) равносоставлены. По транзитивности отношения равносоставленности  равносоставлен с
равносоставлен с  .
.
Лемма 6. Каждый выпуклый многоугольник равносоставлен с некоторым треугольником.
Проверим утверждение для n =4, воспользуемся рисунком 102. В левой его части – четырехугольник  преобразован в равносоставленный с ним треугольник
преобразован в равносоставленный с ним треугольник 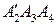 с помощью построения, описанного на странице 105.
с помощью построения, описанного на странице 105.  и четырехугольник
и четырехугольник  имеют общую часть
имеют общую часть  и в их состав входят
и в их состав входят  и
и  , находящиеся в условиях леммы 3. Отсюда
, находящиеся в условиях леммы 3. Отсюда  равносоставлен с четырехугольником
равносоставлен с четырехугольником  . Таким образом лемма верна для n =4.
. Таким образом лемма верна для n =4.
Допустим, что она справедлива и для (n – 1) – угольника. Пусть  – выпуклый n -угольник. Построим равносоставленный с ним (n –1) – угольник тем приемом, который использован при построении треугольника, равносоставленного с четырехугольником (рис. 105). Получаем
– выпуклый n -угольник. Построим равносоставленный с ним (n –1) – угольник тем приемом, который использован при построении треугольника, равносоставленного с четырехугольником (рис. 105). Получаем  который равносоставлен с данным n -угольником.
который равносоставлен с данным n -угольником.
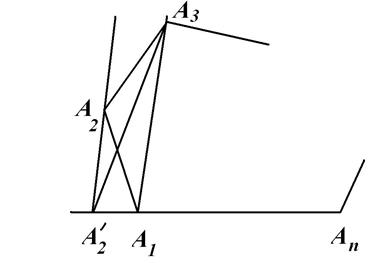
Рис. 105
Допустим, что существует треугольник  , равносоставленный с (n –1)-угольником, тогда по транзитивности этот треугольник равносоставлен с данным n –угольником. Таким образом, из допущения справедливости леммы для n –1 вытекает её верность и для n. В силу аксиомы индукции полученные результаты означают, что лемма 6 верна для любого значения n (начиная с n =4).
, равносоставленный с (n –1)-угольником, тогда по транзитивности этот треугольник равносоставлен с данным n –угольником. Таким образом, из допущения справедливости леммы для n –1 вытекает её верность и для n. В силу аксиомы индукции полученные результаты означают, что лемма 6 верна для любого значения n (начиная с n =4).
Теорема Больяи-Гервина: Равновеликие многоугольники равносоставлены.
Пусть M 1 и M 2 – два равновеликих многоугольника. Согласно лемме 6 существуют треугольники  и
и  , равносоставленные с этими многоугольниками:
, равносоставленные с этими многоугольниками:  – с M 1 и
– с M 1 и  – с M 2. Так как M 1 равновелик
– с M 2. Так как M 1 равновелик  , а M 2 равновелик
, а M 2 равновелик  , то
, то  равновелик
равновелик  . В силу леммы 5
. В силу леммы 5  равносоставлен
равносоставлен  . Теперь по транзитивности отношения равносоставленности получаем равносоставленность и многоугольников M 1 и M 2.Итак, для выпуклых и даже простых многоугольников из их равновеликости следует и их равносоставленность.
. Теперь по транзитивности отношения равносоставленности получаем равносоставленность и многоугольников M 1 и M 2.Итак, для выпуклых и даже простых многоугольников из их равновеликости следует и их равносоставленность.
Обратное – следствие первого и второго условий определения площади фигуры. Таким образом, эти понятия, в своем роде, оказываются для простых многоугольников эквивалентными. Именно это и дает простой прием вычисления площади многоугольных фигур, основанный на конечной процедуре их разбиения на конечное число треугольников.
Совсем иначе дело обстоит с определением объема многогранника.
2  . О равновеликости и равносоставленности многогранников.
. О равновеликости и равносоставленности многогранников.
Многие примеры показывают, что равновеликие простые многогранники равносоставлены, так наклонный параллелепипед равносоставлен с равновеликим ему прямым параллелепипедом. В конце XIX века были указаны примеры равновеликих треугольных пирамид и кубов, которые одновременно являлись и равносоставленными. В 1900 году было получено, что любые два равновеликих многогранника можно разбить на попарно равновеликие тетраэдры. Однако, оставался открытым вопрос о равносоставленности равновеликих многогранников. В связи с этим Д. Гильбертом он был включен в число двадцати трех нерешенных проблем, которые он сформулировал и поставил в 1900 году на втором международном математическом конгрессе. Задача о соотношении между равновеликостью и равносоставленностью простых многогранников и вошла в историю математики как третья проблема Гильберта. Эта проблема была решена учеником Гильберта Максом Деном (1872-1952 гг.) в 1901 году. Ден доказал теорему, из которой следует существование равновеликих, но неравносоставленных многогранников. Её элементарное доказательство было в последствии дано профессором Московского университета В. Ф. Каганом. Приведем формулировку этой теоремы. Обозначим сначала  и
и  двугранные углы многогранников
двугранные углы многогранников  и
и  (
( и
и  – радианные меры углов).
– радианные меры углов).
Теорема. Если многогранники  и
и  равносоставлены, то существуют натуральные числа
равносоставлены, то существуют натуральные числа  и
и  ,где m и n – числа ребер многогранников
,где m и n – числа ребер многогранников  и
и  ,такие, что
,такие, что  .
.
Мы не будем приводить здесь доказательство этой теоремы, ограничившись следствием о неравносоставленности куба и правильного тетраэдра, имеющих равные объемы.
Пусть  – двугранный угол тетраэдра.
– двугранный угол тетраэдра.  (найти это значение
(найти это значение  предлагается читателю). Двугранный угол куба равен
предлагается читателю). Двугранный угол куба равен  (
( ). Если допустить, что куб и тетраэдр равносоставлены, то согласно теореме Дена существуют натуральные p и q, для которых
). Если допустить, что куб и тетраэдр равносоставлены, то согласно теореме Дена существуют натуральные p и q, для которых  (k – число целое). Отсюда
(k – число целое). Отсюда  . Поэтому
. Поэтому  равен либо 0, либо 1, либо –1, т. е. числу целому. С другой стороны, из того, что
равен либо 0, либо 1, либо –1, т. е. числу целому. С другой стороны, из того, что  ,следует
,следует 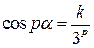 . Например,
. Например,  ,
,  и т. д.. При этом дробь
и т. д.. При этом дробь  – несократимая при любом k, таким образом
– несократимая при любом k, таким образом  – несократимая дробь, т. е. число нецелое. Получили противоречие с результатом допущения:
– несократимая дробь, т. е. число нецелое. Получили противоречие с результатом допущения:  – число целое. Это противоречие заставляет отбросить допущение и принять, что куб и правильный тетраэдр неравносоставлены.
– число целое. Это противоречие заставляет отбросить допущение и принять, что куб и правильный тетраэдр неравносоставлены.
Заметим в заключении, что «наугад» взятые равновеликие многогранники скорее всего неравносоставлены.
Необходимость привлечения теории пределов при нахождении объема тетраэдра как раз и является следствием теоремы Дена.
Рекомендуемая литература
1. Д. Гильберт, Основания геометрии, М., 1948 г.
2. С. В. Бахвалов, В. П. Иваницкая, Основания геометрии, М., 1972.
3. И. П. Егоров, Геометрия, М., 1979.
4. В. Ф. Каган, Основания геометрии, часть I, М., 1949 г.
5. А. Д. Александров, Н. Ю. Нецветаев, Геометрия, М., 1990 г.
6. Ф. Бахман, Построение геометрии на основе понятия симметрии, М., 1969 г.
7. Д. И. Перепелкин, Курс элементарной геометрии, ч. I и ч. II, М., 1948, 1949 г.г.
8. Энциклопедия элементарной математики, т. IV, М., 1963 г.
9. Ж. Адамар, Элементарная геометрия, ч. I и ч. II, М., 1952, 1957 г.
10. Г. С. М. Кокстер, С. Л. Грейтцер, Новые встречи с геометрией, М., 1978 г.
11. Н. Ф. Четверухин, Изображение фигур в курсе геометрии, М., 1958 г.
12. Н. Ф. Четверухин, Стереометрические задачи на проекционном чертеже, М., 1953 г.
13. Б. И. Аргунов, М. Б. Балк, Элементарная геометрия, М., 1966 г.
14. В. Г. Болтянский, Элементарная геометрия, М., 1985 г.
15. А. П. Киселев, Геометрия, часть I и часть II.
16. Г. Шоке, Геометрия, М., 1970 г.
17. Е. Е. Вересова, Н. С. Денисова, Т. Н. Полякова, Практикум по решению математических задач, М.,1979 г.
Оглавление
Предисловие.......................................... стр. 3
Введение..............................................стр. 4
Лекция 1..............................................стр. 10
Лекция 2.............................................. стр. 29
Лекция 3.............................................. стр. 54
Лекция 4.............................................. стр. 64
Лекция 5.............................................. стр. 76
Лекция 6..............................................стр. 104
Рекомендуемая литература.............................. стр. 111





 и «добавляем его» к параллелограмму, получаем прямоугольник
и «добавляем его» к параллелограмму, получаем прямоугольник  , площадь которого есть сумма площадей двух фигур, из которых состоит параллелограмм
, площадь которого есть сумма площадей двух фигур, из которых состоит параллелограмм  . На этом основании заключаем, что площадь параллелограмма равна площади прямоугольника.
. На этом основании заключаем, что площадь параллелограмма равна площади прямоугольника.

 .
.
 .
.
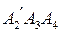 (в общем случае
(в общем случае  ) имеет площадь равную площади исходного многоугольника. Следует, однако, заметить разницу с предыдущими случаями перестроения данной фигуры, которая состоит в том, что данная фигура и построенная, строго говоря, имеют равные площади не потому, что составлены из попарно равных фигур, а потому, что одна, или несколько, как в правой части рисунка, пар треугольников – треугольники, имеющие равные площади, хотя они и не равны друг другу.
) имеет площадь равную площади исходного многоугольника. Следует, однако, заметить разницу с предыдущими случаями перестроения данной фигуры, которая состоит в том, что данная фигура и построенная, строго говоря, имеют равные площади не потому, что составлены из попарно равных фигур, а потому, что одна, или несколько, как в правой части рисунка, пар треугольников – треугольники, имеющие равные площади, хотя они и не равны друг другу. . Равновеликость и равносоставленность многоугольников.
. Равновеликость и равносоставленность многоугольников. , находящиеся в условиях леммы. Равносоставленность этих фигур видна из рисунка.
, находящиеся в условиях леммы. Равносоставленность этих фигур видна из рисунка.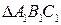 с равными основаниями BC и B 1 C 1 и равными высотами, опущенными из A и A 1 соответственно на BC и B 1 C 1, переходим к параллелограммам с равными сторонами и равными высотами, которые равносоставлены по лемме 1. Каждый из них равносоставлен с треугольниками
с равными основаниями BC и B 1 C 1 и равными высотами, опущенными из A и A 1 соответственно на BC и B 1 C 1, переходим к параллелограммам с равными сторонами и равными высотами, которые равносоставлены по лемме 1. Каждый из них равносоставлен с треугольниками  и
и  .
. и при этом
и при этом  (рис. 103).
(рис. 103).
 , а от
, а от  . Последние равновелики друг другу по транзитивности. Затем от параллелограмма
. Последние равновелики друг другу по транзитивности. Затем от параллелограмма  ,а от параллелограмма
,а от параллелограмма  . Прямоугольники так же равновелики. Так у этих прямоугольников по условию
. Прямоугольники так же равновелики. Так у этих прямоугольников по условию  равны в силу известного выражения площади прямоугольника в виде произведения его смежных сторон (см. лекцию 5, пункт
равны в силу известного выражения площади прямоугольника в виде произведения его смежных сторон (см. лекцию 5, пункт  ). Но A2B и
). Но A2B и 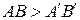 (рис. 104).
(рис. 104).
 проводим прямую l параллельно
проводим прямую l параллельно  и, построив окружность
и, построив окружность  , отмечаем точку A 1 пересечения l с окружностью
, отмечаем точку A 1 пересечения l с окружностью  равносоставлен с
равносоставлен с  равновелик
равновелик  , а значит равновелик и треугольнику ABC. Треугольники
, а значит равновелик и треугольнику ABC. Треугольники  . По этой причине в силу леммы 4
. По этой причине в силу леммы 4  . Тогда по лемме 3 эти треугольники (т. е.
. Тогда по лемме 3 эти треугольники (т. е.  преобразован в равносоставленный с ним треугольник
преобразован в равносоставленный с ним треугольник 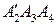 с помощью построения, описанного на странице 105.
с помощью построения, описанного на странице 105.  и четырехугольник
и четырехугольник  и в их состав входят
и в их состав входят  , находящиеся в условиях леммы 3. Отсюда
, находящиеся в условиях леммы 3. Отсюда  – выпуклый n -угольник. Построим равносоставленный с ним (n –1) – угольник тем приемом, который использован при построении треугольника, равносоставленного с четырехугольником (рис. 105). Получаем
– выпуклый n -угольник. Построим равносоставленный с ним (n –1) – угольник тем приемом, который использован при построении треугольника, равносоставленного с четырехугольником (рис. 105). Получаем  который равносоставлен с данным n -угольником.
который равносоставлен с данным n -угольником.
 , равносоставленный с (n –1)-угольником, тогда по транзитивности этот треугольник равносоставлен с данным n –угольником. Таким образом, из допущения справедливости леммы для n –1 вытекает её верность и для n. В силу аксиомы индукции полученные результаты означают, что лемма 6 верна для любого значения n (начиная с n =4).
, равносоставленный с (n –1)-угольником, тогда по транзитивности этот треугольник равносоставлен с данным n –угольником. Таким образом, из допущения справедливости леммы для n –1 вытекает её верность и для n. В силу аксиомы индукции полученные результаты означают, что лемма 6 верна для любого значения n (начиная с n =4). и
и  , равносоставленные с этими многоугольниками:
, равносоставленные с этими многоугольниками:  и
и  двугранные углы многогранников
двугранные углы многогранников  и
и  (
( и
и  – радианные меры углов).
– радианные меры углов). и
и  ,где m и n – числа ребер многогранников
,где m и n – числа ребер многогранников  .
. – двугранный угол тетраэдра.
– двугранный угол тетраэдра.  (найти это значение
(найти это значение  предлагается читателю). Двугранный угол куба равен
предлагается читателю). Двугранный угол куба равен  (
( ). Если допустить, что куб и тетраэдр равносоставлены, то согласно теореме Дена существуют натуральные p и q, для которых
). Если допустить, что куб и тетраэдр равносоставлены, то согласно теореме Дена существуют натуральные p и q, для которых  (k – число целое). Отсюда
(k – число целое). Отсюда  . Поэтому
. Поэтому  равен либо 0, либо 1, либо –1, т. е. числу целому. С другой стороны, из того, что
равен либо 0, либо 1, либо –1, т. е. числу целому. С другой стороны, из того, что 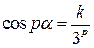 . Например,
. Например,  ,
,  и т. д.. При этом дробь
и т. д.. При этом дробь  – несократимая при любом k, таким образом
– несократимая при любом k, таким образом 


