О понятиях, используемых в учебных курсах геометрии без определений. Геометрическая фигура как «геометрическое место точек».

1º. Наряду с основными (базовыми) понятиями, прямого определения которым не дается по принципиальным причинам логического характера, в геометрии и особенно в ее учебных курсах широко используются без определений ряд понятий, не относящихся к понятиям основным, базовым. Примером тому служат прежде всего понятия «фигура», «тело», «поверхность», «линия». Возникает естественный вопрос о причинах такого положения, тем более, что оно сохраняется и в современных учебных курсах, претендующих на повышенную строгость изложения вплоть до представления в них полного списка аксиом. В настоящей лекции эти понятия будут раскрыты, в первую очередь, через демонстрацию математической сущности этих понятий.

Математическое понятие определяемо, если его математическое содержание можно раскрыть через другие понятия теории по схеме: род и видовое отличие, то есть путем указания:

1. понятия, к которому определяемое относится и

2. последующего перечисления особенностей определяемого, выраженных на языке других ранее известных понятий.

Классический пример: «параллелограмм – это четырехугольник, пары противоположных сторон которого принадлежат парам параллельных прямых». Подчеркнутое понятие можно рассматривать как род понятия «параллелограмм», причем само понятие «четырехугольник» естественно должно быть ранее определено. Видовые отличия выражены через ранее известные понятия «противоположные стороны» и «параллельные прямые». Это логическое требование к определениям понятий математической теории и приводит с неизбежностью к таким понятиям, которые уже невозможно определить в указанном выше смысле. Их приходится, как говорят «принимать без определения», ограничиваясь перечислением их необходимых и достаточных для соответствующей теории свойств. Утверждения, представляющие основные свойства неопределяемых понятий и называют аксиомами.

Возможно ли определить понятие «фигура» через основные понятия геометрии, например, в гильбертовском варианте? Если бы это было возможно, то сами первичные понятия геометрической системы нельзя было бы отнести к классу фигур, что как мы знаем не соответствует сложившейся традиции: и точка, и прямая, и плоскость трактуются нами как конкретного вида фигуры. Таким образом, термин «фигура» естественно рассматривать как название самого общего рода геометрических понятий, когда последние определяются нами по схеме «род и видовое отличие»: окружность – это фигура и т.д., многоугольник – это фигура и т.д. Значит, в иерархии геометрических понятий «фигура» выступает как понятие максимального объема, максимальной емкости, а потому в принципе не может быть определено через основные, базовые, понятия геометрии (известный вариант определения «фигуры» опирается на понятие, не принадлежащее геометрии).

По этой причине, если мы хотим пользоваться понятием «фигура», то его придется рассматривать как еще одно основное, неопределяемое понятие, содержание которого должно быть раскрыто в ряде принимаемых нами соглашений - аксиом.

Анализ вариантов использования понятия «фигура» указывает на то, что с этим понятием связаны отношения принадлежности точки фигуре и совпадения (равенства) фигур, а так же условие существования фигуры. Таким образом, основные понятия – точка и фигура, основное отношение – точка принадлежит фигуре. Обозначив фигуры большой буквой F с индексами, а принадлежность знаком , сформулируем аксиомы «фигуры».

Аксиомы.

1. Точка есть фигура.

2. Если из М F ₁ следует M F ₂, а из N F ₂ следует N F ₁, то F ₁ и F ₂ – различные обозначения одной и той же фигуры. В этом случае говорим, что F ₁ равна F ₂ и пишем F ₁ = F ₂.

3. Фигура F существует, если существует хотя бы одна точка, принадлежащая фигуре F.

Последняя аксиома предполагает заданным условие, позволяющее решать вопрос о принадлежности точки фигуре, при этом, естественно, что это условие должно быть выражено в терминах рассматриваемой геометрической системы. Так как принадлежность точки прямой или плоскости проверяема с точки зрения гильбертовской аксиоматики, то прямые и плоскости мы относим к геометрическим фигурам. Для задания прямой в геометрии Евклида достаточно указать две точки, для задания плоскости – три точки общего положения, для задания окружности или сферы – три, или соответственно четыре точки общего положения и т.д. и т.п.

Как фигура может быть задана? Первое – путем указания набора точек, который позволит решить вопрос о принадлежности произвольной точки рассматриваемой фигуре. Второе – путем задания так называемого характеристического свойства точек, принадлежащих фигуре. Это свойство, во-первых, выражается в терминах рассматриваемой теории, а во-вторых, определяет фигуру в том смысле, что позволяет решать вопрос о принадлежности точки фигуре: всякая точка пространства принадлежит фигуре тогда и только тогда, когда она обладает указанным свойством. Если фигура задается характеристическим свойством точек, ей принадлежащих, то она со времен Евклида, имеет название геометрического места точек.

О фигурах, как геометрических местах точек, поговорим позднее, а сейчас обратимся к трем понятиям, которые в учебных курсах геометрии используются без определений.

 

 

2º. Тело, поверхность, линия.

Прежде всего заметим, что эти понятия в отличии от понятия «фигура» – понятия определяемые, но их определения зависят от той трактовки, которая характерна для соответствующей математической теории. В евклидовой геометрии эти понятия трактуются со времен Евклида как: ограниченная часть пространства – тело, граница тела – поверхность и соответственно линия – граница поверхности. Используя именно такие, хотя и расплывчатые, представления об этих фигурах, покажем, как они могут быть определены в терминах евклидовой геометрии.

Основным понятием, которое мы используем в определениях понятий тело, поверхность, линия, будет понятие окрестности точек, трактуемое как открытый шар, то есть шар без точек его поверхности, центром которого является сама рассматриваемая точка. При этом сам термин «шар» имеет значение, зависящее от размерности пространства, в котором рассматривается точка и ее окрестность. Для пространства одномерного (прямой) этот «шар» называют интервалом, для случая двумерного пространства (плоскости) «шар» - это круг с центром в рассматриваемой точке. В трехмерном пространстве или как мы говорим просто «в пространстве» «шар» - это соответствующая пространственная фигура хорошо знакомая читателю. Таким образом, окрестность точки О есть фигура, каждая точка которой удалена от О на расстояние, меньшее заданной величины r (отрезка r). При необходимости окрестность точки О можно обозначить парой (О, r). Саму точку О можно отнести к ее окрестности

 

Определение. Фигуру F пространства называют телом, если она представляет собой ограниченную, замкнутую область пространства.

 

Раскроем содержание понятий замкнутая и ограниченная область. Для этого придется ввести ряд понятий, которые мы сейчас последовательно рассмотрим.

 

Понятие первое: точка М называется точкой сгущения фигуры F, если в любой ее окрестности содержатся точки этой фигуры.

 

Обратим внимание на то, что сама точка М может как принадлежать фигуре F, так ей и не принадлежать.

Пример: F – шар. Внутренняя точка шара – точка сгущения принадлежит шару, точка поверхности шара – точка сгущения шара вне зависимости от того какой шар мы рассматриваем: вместе с его поверхностью или без нее. В первом случае – это точка шара, а во втором – она ему не принадлежит. Таким образом, точка сгущения фигуры может как принадлежать так и не принадлежать самой фигуре.

 

Второе понятие: F называется замкнутой фигурой, если она содержит все свои точки сгущения.

 

Третье понятие: F- связная фигура, если любые две ее точки можно соединить ломаной линией, каждая точка которой принадлежит фигуре F.

 

Четвертое понятие: Фигура F называется ограниченной, если существует шар, которому принадлежит каждая точка фигуры F.

 

Примерами неограниченных фигур являются прямая, плоскость, луч, полуплоскость.

 

Пятое понятие: М – внутренняя точка фигуры F, если М F и существует окрестность точки М, принадлежащая фигуре F.

 

Если есть окрестность точки М, никакая точка которой не принадлежит F, то М – внешняя точка для фигуры F. Если в любой окрестности М имеются точки, принадлежащие F и точки ей не принадлежащие, то М называем граничной точкой F. Сама граничная точка может принадлежать F, а может ей и не принадлежать. Фигура, каждая точка которой является граничной точкой фигуры F, называется границей F. У замкнутой фигуры ее граница принадлежит фигуре, а у незамкнутой граница ей не принадлежит.

 

Шестое понятие: Область пространства – связная ограниченная фигура, каждая точка которой является ее внутренней точка.

 

Перечисленные понятия полностью раскрывают содержание понятия «тело» в том смысле, в каком оно используется, по крайней мере, в евклидовой геометрии. Примером тел, изучаемых в школьном курсе геометрии, являются призмы, пирамиды и тела вращения. Соответствующие фигуры с теми же названиями рассматриваются и как поверхности: говорят о цилиндрической, конической, сферической поверхностях, поверхностях призм и пирамид.

Понятие поверхности, в наглядном смысле трактуемое как граница тела, может быть раскрыто по той же схеме и с использованием тех же вспомогательных понятий, которые мы использовали в определении понятия «тело». Поэтому позволим себе представить это понятие в обзорном порядке.

 

Определение 1: Фигура F называется полной поверхностью, или оболочкой, если она является границей некоторого тела Т.

 

Поверхность рассматривается как часть оболочки некоторого тела. Для формального определения этого понятия вводится понятие внутренней точки такой фигуры, ее граничной точки и границы этой фигуры, а также понятие связности фигуры, принадлежащей оболочке.

Фигура Х называется областью на оболочке F, если все ее точки являются внутренними точками оболочки, а сама фигура Х является связной на F. Область Х на F замкнута, если ей принадлежат все ее граничные точки. Отсюда получаем.

 

Определение 2: Фигура Р называется поверхностью, если существует такая область Х на оболочке F, замыкание которой и есть фигура Р.

 

Говоря об определении линии, мы имеем в виду лишь такую линию, которая может быть границей поверхности. В современной математике понятие линии значительно расширено и его наиболее общее определение связано с понятием одномерного многообразия как топологического образа ломаной линии.

Если Р – какая-либо поверхность, то можно говорить о границе этой поверхности как фигуре, содержащей граничные точки поверхности Р. Но в этом случае фигура Р будет представлять замкнутую линию, в то время как очень часто приходится рассматривать и незамкнутые линии. Значит, следует определять это понятие так, чтобы и этот случай не был потерян.

Назовем границу поверхности ее полным контуром, тогда фигура F принадлежащая контуру поверхности Р, называется линией, если F – такая область на Р, замыканием которой служит сама фигура F.

Определения понятию «линия» в современном расширенном смысле впервые были даны Г.Кантором (1845 - 1918 г.г.) и П.С.Урысоном (1898 – 1924 г.г.), причем Урысон обобщает определение Кантора (см., например, А.С.Пархоменко, «Что такое линия?», М. 1954г.).

 

3º. Некоторые геометрические места точек.

Рассмотрим примеры фигур, которые определяются как геометрические места точек. Договоримся для удобства сокращать это название и писать «г.м.т.».

Первыйклассг.м.т. В определениях г.м.т. этого класса используется как основное, понятие «расстояние». При этом под расстоянием от точки М до фигуры F будем понимать наименьший из всех отрезков, соединяющих точку М с каждой точкой фигуры F.

Рассмотрим примеры двух типов таких г.м.т.

1-й тип – г.м.т., каждая из которых удалена от данной фигуры F на заданное расстояние h. Выбирая конкретные F и h, мы обращаемся к конкретному г.м.т.

Пример 1. Фигура – точка О, расстояние – конкретный отрезок h.

В этом случае наше г.м.т. есть известная фигура – окружность, в случае, когда мы рассматриваем г.м.т. в плоскости, (двумерном пространстве), сфера, если речь идет о г.м.т. в пространстве (трехмерном пространстве). О – центр окружности, или сферы соответственно, h – их радиус, обозначение – (О, h).

Пример 2. Фигура – прямая а, расстояние – отрезок h. Рассматривается г.м.т., каждая из которых удалена от а на расстояние h.

Если рассматриваем это г.м.т. в двумерном пространстве, то оно представляет собой пару прямых, параллельных прямой а, расположенных по разные стороны от а (рис. 1).

 

Рис. 1

 

Прямые, составляющие г.м.т., изображены штриховой линей. Доказательство проводить не будем, но отметим его шаги:

1. Доказывается существование точки, удаленной от а на расстояние h;

2. Через полученную точку (например, M_i) проводится прямая , параллельная прямой а, а через N_i проводится прямая n, параллельная а.

3. Доказывается, что всякая точка г.м.т. принадлежит либо m, либо n, а всякая точка этих прямых принадлежит г.м.т.

На этом основании и делается заключение, что г.м.т. есть пара прямых (m, n).

Пример 3. Г.м.т. плоскости, удаленных на данное расстояние h от данного отрезка АВ.

Это г.м.т. представляет собой пару отрезков M ₁ N ₁ и M ₂ N ₂ и пару полуокружностей с центрами А и В и радиусами равными h. Эту фигуру можно назвать «беговой дорожкой» (рис. 2).

 

Рис. 2

 

Для исследования вида этого г.м.т. целесообразно через точки А и В провести перпендикуляры к прямой АВ в концах данного отрезка и исследовать наличие точек, удаленных от отрезка АВ на расстояние h в полосе между перпендикулярами и в двух полуплоскостях, для которых эти перпендикуляры – граничные прямые и точки отрезка АВ этим полуплоскостям не принадлежат. В полосе часть г.м.т. – это пара отрезков M ₁ N ₁ и M ₂ N ₂, а в полуплоскостях – это дуги окружностей (A, h) и (B, h).

Пример 4. Г.м.т. плоскости, удаленных на расстояние h от данной окружности (O, R).

Рассмотрим этот пример подробнее. Будем решать вопрос о существовании точек этого г.м.т., разделив плоскость на две части: область, ограниченную окружностью и область, точки которой лежат вне круга, ограниченного окружностью. Так как точки, лежащие в первой области (круге), удалены от окружности (O, R) на расстояние, меньшее R, а точки, лежащие вне круга (O, R), находятся от нее на расстоянии большем R, то следует рассматривать три случая соотношения между h и R: h < R, h = R и h > R.

В первом случае, очевидно, что точки, удаленные от (O, R) на расстояние h, существуют как внутри круга(O, R), так и вне его (рис. 3).

1. Фиксируем какой-нибудь радиус ОА. От точки А откладываем в направлении к О на радиусе ОА отрезок . Получаем точку М ₁, лежащую внутри круга (O, R) на расстоянии h от окружности.

2. Точно так же откладываем на луче ОА от точки А вне круга (O, R) отрезок . Получаем точку М ₂ вне (O, R), которая удалена от окружности на расстояние h.

 

Точка любой из окружностей (O, R - h) и (O, R + h) удалена от (O, R) на расстояние h.

Обратное, любая точка M _i, удаленная от окружности (O, R) на расстояние h, принадлежит одной из окружностей (O, R - h) или (O, R + h). Таким образом, в рассматриваемом случае исследуемое г.м.т. есть пара окружностей (O, R - h) и (O, R + h).

Во втором случае, когда , г.м.т. состоит из точки О и окружности (O, R + h).

В третьем случае г.м.т. содержит только точки, лежащие вне круга (O, R), и представляет собой окружность (O, R + h).

В качестве упражнения для самостоятельной работы рекомендуем обобщить рассмотренные примеры, рассмотрев г.м.т. с тем же определением, но в трехмерном пространстве.

Перейдем к примерам г.м.т. 2-ого типа.

2-й тип г.м.т. первого класса – это г.м.т., каждая из которых равноудалена от двух данных фигур F ₁ и F ₂.

Как и в предыдущем случае, задавая конкретные фигуры F ₁ и F ₂, получаем конкретные г.м.т. второго типа.

Пример 1. Фигура F ₁ – точка А, фигура F ₂ – точка В.

Речь пойдет о г.м.т., равноудаленных от точек А и В. Используем, как известный факт, вопрос о существовании середины отрезка. Итак, пусть О – середина отрезка АВ. Тогда О – точка, равно удаленная от точек А и В. Проведем через О перпендикуляр к прямой АВ и обозначим его буквой m (рис. 4).

Пусть M – произвольная точка m, отличная от О. Тогда из равенства прямоугольных треугольников АОМ и ВОМ следует , то есть М равноудалена от данных точек А и В.

Вывод: прямая m входит в состав исследуемого г.м.т.

Теперь покажем, что любая точка равноудаленная от А и В, принадлежит перпендикуляру m. Допустим противное, то есть N равноудалена от А и В, но .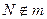

1. из допущения и равенства треугольников AON и BON, а также смежности углов и следует ортогональность прямых ON и AB. В результате

2. имеем два различных перпендикуляра m и ON к прямой АВ, которые проходят через одну точку О. Это противоречит известному факту геометрии Евклида. Такой результат – следствие сделанного выше допущения, значит оно неверно. Таким образом, из двух возможностей и 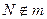верна только первая.

Вывод: Исследуемое г.м.т. есть прямая, перпендикулярная к отрезку, соединяющему точки А и В, в его середине.

Это г.м.т. часто называют «серединным перпендикуляром отрезка», по-гречески – медиатриса отрезка.

 

Пример 2. Фигуры F ₁ и F ₂ – два луча h и k, имеющие общее начало О. Такая пара лучей, как известно, называется углом. Поэтому можно говорить о г.м.т., равноудаленных от сторон угла . Здесь, как и выше, будем вести речь о г.м.т. в плоскости.

Пусть h и k – различные и не принадлежащие одной прямой лучи (рис. 5).

1. Откладываем на h и на k отрезки ОН и ОК, равные между собой.

2. Проводим через Н и К перпендикуляры к сторонам угла .

3. Отмечаем точку пересечения этих перпендикуляров и обозначаем ее М.

Нетрудно видеть, что 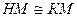, то есть М равноудалена от сторон угла . Значит исследуемое г.м.т. существует. Обратим еще внимание на то, что точка М лежит внутри .

 

Легко видеть, что при любом выборе равных между собой отрезков OH _i и OК _i мы получаем точку M _i, равноудаленную от h и k. Все эти точки принадлежат биссектрисе , которой будет луч ОМ. Таким образом, биссектриса входит в состав рассматриваемого г.м.т.

Теперь отметим еще три области (части плоскости), не являющиеся внутренней областью . Построим лучи m и n, исходящие из О и перпендикулярные соответственно лучам h и k (рис. 6).

У каждого из трех углов , и имеется внутренняя область, их и обозначаем римскими цифрами I, II и III. В областях I и II нет ни одной точки, равноудаленной от сторон . Напротив того, в области III, включая и лучи m и n, каждая точка P _i удалена как от луча h так и от луча k на расстояние P _i O, то есть P _i равноудалена от сторон .

Так же, несложно понять, что и всякая точка, равноудаленная от сторон угла , либо принадлежит его биссектрисе, либо области III, включая и лучи m и n. Следовательно, рассматриваемое г.м.т. есть фигура, состоящая из биссектрисы и части плоскости, ограниченной лучами m и n, перпендикулярными к лучам h и k в их начале О.

Замечание. Рассмотренный пример указывает на то, что биссектрису угла нельзя определять как г.м.т. плоскости, равноудаленных от сторон угла. Заметим также, что для развернутого угла (стороны угла взаимно дополняют друг друга до прямой) это г.м.т. представляет собой прямую, проходящую через вершину угла перпендикулярно прямой, на которой его стороны лежат.

Пример 3. Фигуры F ₁и F ₂ – прямые a и b.

В случае, когда a и b принадлежат одной плоскости, они могут быть либо параллельными, либо пересекающимися. В первом случае соответствующее г.м.т. представляет собой прямую l, являющуюся осью симметрии пары прямых a и b (рис. 7).

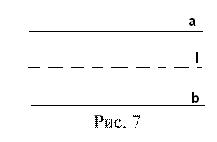
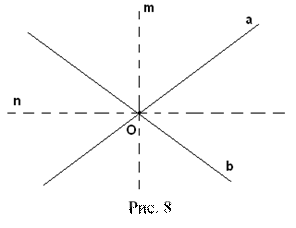
В втором случае г.м.т. состоит из двух взаимно перпендикулярных прямых m и n, проходящих через общую точку прямых а и b, каждая из которых содержит биссектрисы пар вертикальных углов, образованных прямыми a и b (рис. 8).

Пример 4. Одна из фигур F ₁ и F ₂ – окружность, а другая – точка. Окружность обозначим (O, R), точку – А.

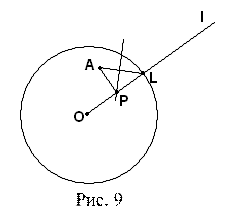
Рассмотрим случай, когда А – внутренняя точка круга (O, R) и отлична от центра О. Проведем луч l из точки О и, отметив точку L его пересечения с (O, R), построим медиатрису отрезка AL (рис. 9).

Точка Р пересечения l с этой медиатрисой равноудалена от А и окружности (O, R), так как расстояние от Р до (O, R) есть отрезок PL, а расстояние от Р до А есть отрезок РА, но 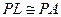, так как Р принадлежит медиатрисе отрезка AL.

Итак, на каждом луче, исходящем из О существует точка, равноудаленная от (O,R) и точки А.

Теперь нетрудно подсчитать, что 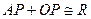, то есть при фиксированных (O, R) и А сумма расстояний от точки Р до точек О и А есть величина постоянная, в нашем случае равная R. Известно, что г.м.т., сумма расстояний которых до двух фиксированных точек равна наперед заданной величине, есть эллипс. Таким образом, в рассматриваемом случае исследуемое г.м.т. является эллипсом, у которого фокусами являются точки О и А.

Другие случаи взаимного расположения окружности и точки рекомендуется исследовать читателю самостоятельно. Кроме того, в качестве упражнения целесообразно рассмотреть и случай, когда обе фигуры F ₁ и F ₂ являются окружностями.

 

Второйклассг.м.т. – г.м.т., из которых данная фигура F видна под данным углом α.

Пример 1. F – отрезок. Г.м.т. плоскости, из которых данный отрезок виден под данным углом α.

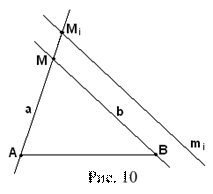Пусть данный отрезок – АВ и данный угол – α.

Построим точку, из которой отрезок АВ виден под углом α. Через А проведем прямую а и отметим на ней произвольно выбранную точку M _i (рис. 10).

С вершиной в точке M _i и стороной M _i A строим угол AM _i m _i, равный углу α и притом так, чтобы луч m _i с началом в точке M _i был расположен с той же стороны от прямой а с какой от а расположена точка В.

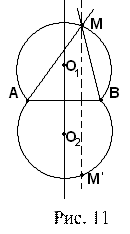Может случиться, что m _i пройдет через В. В этом случае M _i – искомая точка. Если же как на рисунке 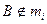, то проводим через В прямую b, параллельную m_i. Эта прямая пересечет луч M_iA в точке М, для которой 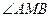равен α. Значит, М – искомая точка исследуемого г.м.т. Используя известную теорему о вписанных в окружность углах, опирающихся на одну и ту же дугу окружности, описанной около 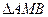, получим – АВ виден под углом α из каждой точки дуги 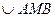. Значит, эта дуга входит в состав исследуемого г.м.т. Если взять еще и дугу окружности, симметричную 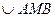, то и точки этой дуги будут обладать тем же свойством, что и точки дуги 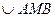(рис. 11). Таким образом, г.м.т. принадлежат эти две дуги окружностей, симметричных друг другу относительно прямой АВ.

Теперь можно убедиться в том, что ни одна из точек плоскости, не лежащих на этих дугах, не входит в состав рассматриваемого г.м.т.

 

Вывод: Г.м.т., из которых данный отрезок виден под данным углом, есть фигура, состоящая из двух дуг равных и симметрично расположенных окружностей, которые стягиваются одной хордой.

Пример 2. Фигура F – окружность, данный угол – α. Найти г.м.т. плоскости, из которых окружность видна под углом α.

Пусть данная окружность обозначена (O, R). Углом видимости окружности из точки называют угол, образованный касательными к окружности, проходящими через эту точку.

Очевидно, что ни одна точка внутри круга (O, R) не может принадлежать исследуемому г.м.т. Таким образом, такие точки нужно искать вне круга (O, R) (рис. 12).

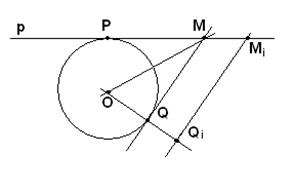
Рис. 12

1. Через произвольную точку Р на окружности (O, R) проводим к ней касательную р.

2. Возьмем на р произвольную точку M_i и с вершиной в этой точке и стороной M_iP строим угол, равный α, вторая сторона которого M_iQ_i лежала бы с той же стороны от прямой р, с какой лежит и окружность (O, R).

Может случиться, что M_iQ_i будет касаться (O, R). Тогда M_i – искомая точка. В общем случае M_iQ_i не касается (O, R). В этом случае:

1. через О проводим перпендикуляр к M_iQ_i, на рисунке он пересекает луч M_iQ_i в точке Q_i. Пусть Q – точка пересечения OQ_i с окружностью (O, R).

2. через Q проводим касательную к окружности. Она пересечет прямую p в точке M. 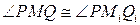, а значит и 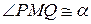. Точка M – искомая, точка, принадлежащая исследуемому г. м. т. Расстояние от M до центра О равно , т. е. эта величина постоянная для любой точки М, она определяется данными величинами R и .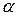

Вывод. Окружность (О, ОМ) входит в состав рассматриваемого г. м. т.

Несложно доказать, что для всякой точки 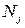искомого г. м. т. расстояние 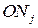равно . Значит 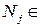(О, ОМ).

Заключение. Исследовавшееся г. м. т. есть окружность (О, ).

Третий класс г. м. т. Г. м. т., отношения расстояний которых до двух заданных точек А и В равны данному числу .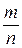

Исследуем это г. м. т. Разделим отрезок АВ внешним и внутренним образом в отношении 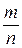. (рис. 13).

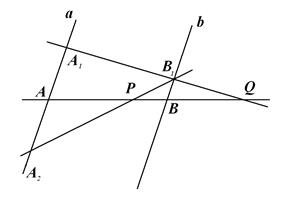
Рис. 13

1. Через А и В проведем параллельные между собой прямые a и b.

2. Выберем отрезок, который обозначим е.

3. Строим отрезки me и ne.

4. На a в обе стороны от точки А откладываем отрезки АА ₁ и АА ₂, равные me. На b от точки В в одну сторону откладываем отрезок ВВ ₁, равный ne.

 

5. Проведя прямые А ₁ В ₁ и А ₂ В ₁, отмечаем точки их пересечения с прямой АВ и называем их Q и P соответственно. Точка Р делит отрезок АВ внутренним образом в отношении 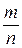, а точка Q –внешним образом в том же отношении. Для доказательства рассматриваем пары подобных треугольников APA ₂ и BPB ₁ и AQA ₁ и BQB ₁. Таким образом мы доказали существование точек, принадлежащих исследуемому г. м. т.

 

Строим окружность с диаметром PQ (рис 14).

Рис. 14

Докажем, что каждая точка этой окружности принадлежит рассматриваемому г. м. т.

Пусть М – точка окружности. Соединяем точку М с А и В и проводим прямые МР и MQ. Через точку В проводим прямую, параллельную АМ. Точки её пересечения с прямыми МР и MQ обозначим буквами С и D.

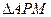подобен 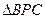и 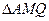подобен 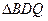. Из подобий треугольников этих пар получаем 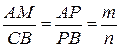(1) и 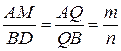(2). Отсюда , а потому .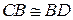

Угол 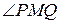опирается на диаметр PQ построенной окружности, а потому этот угол прямой. Таким образом, 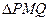– прямоугольный и в нем CD – гипотенуза, а МВ – медиана. По свойству медианы прямоугольного треугольника, проведенной из вершины прямого угла, получаем 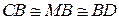. Заменяя либо в пропорции (1), либо в пропорции (2) СВ или соответственно BD на МВ, получаем 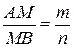. Таким образом, любая точка M рассматриваемой окружности принадлежит исследуемому г. м. т., иначе говоря, окружность с диаметром PQ входит в состав рассматриваемого г. м. т.

Пусть теперь N – точка г. м. т., не принадлежащая прямой АВ. Для неё 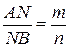(рис.15).

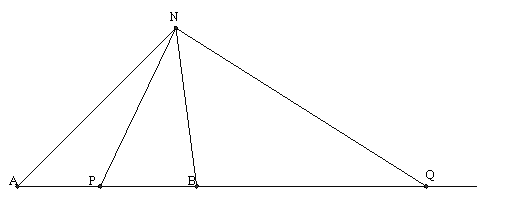
Рис. 15

В силу условия и построения точек P и Q имеем: 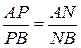(1) и 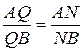(2). Используя теоремы о внутреннем и внешнем угле треугольника заключаем: NP – биссектриса внутреннего угла 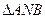, а NQ – биссектриса его внешнего угла, смежного с углом 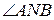. Но биссектрисы таких углов взаимно перпендикулярны. Это означает, что 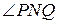– прямой. Отсюда следует, что окружность с диаметром PQ содержит точку N. Итак, любая точка исследуемого г. м. т. принадлежит окружности с диаметром PQ.

 

Вывод: Г. м. т., отношения расстояний которых до двух данных точек А и В равно заданному числу 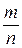, есть окружность, концы одного из диаметров которой делят отрезок АВ внутренним и внешним образом в отношении .

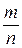Эта окружность получила название окружности Аполлония по имени одного из крупнейших математиков эллинистического периода её зарождения и развития Аполлония Пергского (265-170 г. г. до н. э.).

В заключении нашей темы рассмотрим ещё одно замечательное г. м. т. плоскости под названием радикальная ось двух окружностей.

Предварительно введем понятие «степень точки» относительно окружности. Итак, на плоскости зафиксирована окружность (O, R). Степенью точки М относительно (O, R) называем число 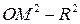. Это число обозначают 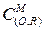или сокращенно .

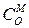1. Если 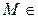(O, R),то 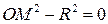. Иначе говоря, точки окружности (O, R) имеют нулевые степени и наоборот, точки имеющие нулевую степень относительно (O, R), принадлежат этой окружности.

2. Степени точек, лежащих вне круга (O, R) – положительные числа (верно и обратное). Кроме того, степень точки, внешней относительно (O, R) можно представить квадратом длины касательной к окружности, проведенной к ней из данной точки.

3. Степени точек, лежащих внутри круга (O, R) – числа отрицательные, причем наименьшее число – R ². Таким образом, существует точка плоскости, имеющая наименьшую степень, этой точкой является центр О окружности (O, R).

Одной из естественных задач становится задача о существовании точек, имеющих равные степени относительно двух или трех окружностей. Решением этой задачи мы и займемся сейчас. Итак, существуют ли на плоскости точки, имеющие равные степени относительно двух окружностей, и что представляет собой фигура, точки которой обладают таким свойством?

Прежде всего, легко понять, что ни одна точка плоскости не может иметь равных степеней относительно концентрических окружностей, так как из 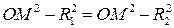следует равенство 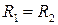, чего не может быть для концентрических окружностей (O, R₁) и (O, R₂). Поэтому в дальнейшем, говоря о паре окружностей, мы имеем в виду только окружности неконцентрические.

Ясно так же, что для окружностей, имеющих хотя бы одну общую точку, эта общая точка и есть точка с равными степенями относительно этих окружностей (степени точки в этом случае нул