Исторически число, выражавшее меру длины отрезка, площади или объема соответствующей фигуры, указывало на число конкретных единиц длины, площади или объема и число их долей, которые содержатся в рассматриваемой геометрической фигуре – отрезке, плоской фигуре (как части плоскости) или фигуре пространственной (как части пространства). В частности, если речь шла о длине отрезка, то выбрав какой-либо отрезок за единичный, решали задачу о нахождении числа, указывающего на количество единичных отрезков и соответствующих его долей, содержащихся в измеряемом отрезке. Выбранному единичному отрезку при этом присваивалось то или иное название, возникшее исторически в той или иной стране, у того или иного народа: сажень, аршин, дюйм, фут и тому подобное. В настоящее время, как мы знаем, наиболее общеупотребляемой мерой длины является метр – отрезок, равный 4 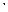 10-7 части парижского меридиана (или 1553164,13 длины волны красной линии спектра кадмия при определенных условиях относительной влажности и состава воздуха, его температуры и давления, ускорения тяжести и других факторах). Соответствующие его десятичные доли получили названия: дециметр, сантиметр, миллиметр и т.д. Отрезки, кратные метру в десятичной системе также получают специальные названия, например, километр.
10-7 части парижского меридиана (или 1553164,13 длины волны красной линии спектра кадмия при определенных условиях относительной влажности и состава воздуха, его температуры и давления, ускорения тяжести и других факторах). Соответствующие его десятичные доли получили названия: дециметр, сантиметр, миллиметр и т.д. Отрезки, кратные метру в десятичной системе также получают специальные названия, например, километр.
Нахождение меры той или иной величины осуществлялось и осуществляется конструктивно, то есть путем прямого разбиения измеряемого целого на соответствующие части, принятые за единицу меры и ее соответствующие доли. Мера величины свидетельствовала о числе единиц и ее долей, заполняющих измеряемую фигуру. С математической точки зрения интерес представляет лишь само число с которым связана измеряемая величина и характер его связи с нею. При этом обнаруживается, что естественные свойства такой меры (длины, площади, объема) выражаются в следующих ее свойствах:
1. мера выражается положительным действительным числом;
2. меры равных величин равны;
3. мера величины, составленной из других величин того же рода, равна сумме мер ее составляющих;
4. существует величина, мера которой принята за единицу.
Оказалось, что этих свойств достаточно для полного описания понятий длина, площадь и объем. Таким образом, возникло своего рода аксиоматическое или, как говорят в таких случаях, дескриптивное (буквально - описательное) определение этих понятий.
В наше время в математике и в ее учебных курсах, в частности, понятия длины отрезка, площади плоской фигуры, объема пространственной фигуры предстают как функции, заданные на соответствующих множествах фигур со значениями из области положительных действительных чисел, обладающие указанными выше свойствами, которые можно конкретизировать так:
1. 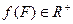 ;
;
2. Если 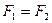 , то
, то 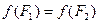 ;
;
3. Если 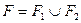 и
и 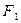 и
и 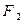 не имеют общих внутренних точек, то
не имеют общих внутренних точек, то 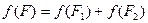 ;
;
4. Существует 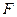 такая, что
такая, что  .
.
Здесь 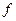 – отображение множества фигур на множество
– отображение множества фигур на множество 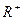 положительных действительных чисел,
положительных действительных чисел, 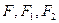 – фигуры, иначе элементы множества фигур. Так как в общем виде, то есть вне зависимости от типа фигур, такая функция, как оказалось, не может быть построена, то рассматривается построение отдельных функций, определяемых на классах конкретных фигур одного вида, если, конечно, в рассматриваемом случае множество фигур допускает его разбиение на классы однотипных фигур. Так, например, для множества отрезков прямой речь может идти только об одном (неделимом) классе фигур, представляющем все множество отрезков пространства. Для множества плоских или пространственных фигур такое разбиение на классы возможно, например, на множество прямоугольников, множество параллелограммов, множество треугольников и т.д. и т.п. Второе, третье и четвертое свойства понятий длины, площади и объема называют соответственно свойствами инвариантности, аддитивности и нормированности меры.
– фигуры, иначе элементы множества фигур. Так как в общем виде, то есть вне зависимости от типа фигур, такая функция, как оказалось, не может быть построена, то рассматривается построение отдельных функций, определяемых на классах конкретных фигур одного вида, если, конечно, в рассматриваемом случае множество фигур допускает его разбиение на классы однотипных фигур. Так, например, для множества отрезков прямой речь может идти только об одном (неделимом) классе фигур, представляющем все множество отрезков пространства. Для множества плоских или пространственных фигур такое разбиение на классы возможно, например, на множество прямоугольников, множество параллелограммов, множество треугольников и т.д. и т.п. Второе, третье и четвертое свойства понятий длины, площади и объема называют соответственно свойствами инвариантности, аддитивности и нормированности меры.
1º Длина отрезка.
Определение: длиной отрезка АВ называется действительное положительное число, поставленное в соответствие отрезку так, что:
1.равным отрезкам соответствуют равные числа;
2.если отрезок равен сумме двух отрезков, то его длин равна сумме длин отрезков-слагаемых;
3. существует отрезок, длина которого равна 1.
Отрезок, длина которого равна 1, называют единичным или единицей измерения. Если для обозначения длины отрезка использовать распространенное функциональное обозначение с использованием в качестве обозначения функции буквы 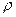 (ро), то длина отрезка
(ро), то длина отрезка 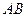 может быть записана как
может быть записана как 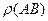 . Алгоритм нахождения длины отрезка
. Алгоритм нахождения длины отрезка 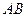 базируется на свойстве Архимеда и аксиоме непрерывности. У Д.Гильберта свойство Архимеда – первая аксиома группы аксиом непрерывности, у С.В.Бахвалова и В.П.Иваницкой свойство Архимеда – следствие аксиомы непрерывности Дедекинда. Суть этого свойства состоит в следующем: для любых отрезков
базируется на свойстве Архимеда и аксиоме непрерывности. У Д.Гильберта свойство Архимеда – первая аксиома группы аксиом непрерывности, у С.В.Бахвалова и В.П.Иваницкой свойство Архимеда – следствие аксиомы непрерывности Дедекинда. Суть этого свойства состоит в следующем: для любых отрезков 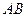 и
и 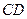 найдется такое натуральное
найдется такое натуральное 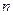 , что
, что 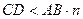 , где
, где

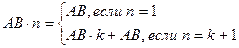
Это свойство влечет за собой существование для 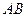 и
и 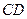 такого целого неотрицательного
такого целого неотрицательного 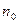 , для которого
, для которого 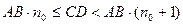 .
.
Для задания функции 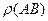 можно использовать известный алгоритм Евклида, когда один из отрезков
можно использовать известный алгоритм Евклида, когда один из отрезков 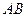 или
или 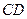 откладывается на другом целое число раз до тех пор, пока это возможно, то есть либо конец последнего откладываемого отрезка совпадет со вторым концом отрезка, на котором первый откладывается, либо расстояние от конца последнего до конца измеряемого будет меньше откладываемого отрезка (см. рис.75).
откладывается на другом целое число раз до тех пор, пока это возможно, то есть либо конец последнего откладываемого отрезка совпадет со вторым концом отрезка, на котором первый откладывается, либо расстояние от конца последнего до конца измеряемого будет меньше откладываемого отрезка (см. рис.75).
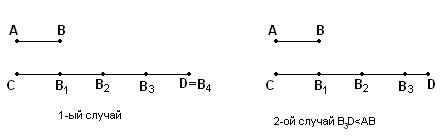
Рис. 75
В последнем случае число 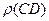 будет представлено в виде цепной дроби. Например, если
будет представлено в виде цепной дроби. Например, если 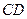 - диагональ квадрата, а
- диагональ квадрата, а 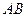 – его сторона, то это число будет представлено бесконечной цепной дробью
– его сторона, то это число будет представлено бесконечной цепной дробью 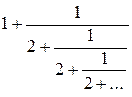 .
.
Но такое представление действительного числа мало используется вообще и незнакомо учащимся средней общеобразовательной школы. Поэтому при конструировании функции 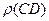 воспользуемся широко известным практическим приемом измерения отрезков, когда на измеряемом отрезке откладывается единичный отрезок, а затем на остатке – десятичные доли единичного отрезка
воспользуемся широко известным практическим приемом измерения отрезков, когда на измеряемом отрезке откладывается единичный отрезок, а затем на остатке – десятичные доли единичного отрезка 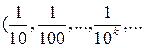 доли единичного отрезка).
доли единичного отрезка).
В этом случае длина отрезка, как число действительное, предстает в виде десятичной систематической дроби.
Именно этим вторым способом построения искомой функции мы и воспользуемся. При этом возникает естественный вопрос: а не зависит ли искомая функция от способа ее задания? Ответ на этот вопрос дает следующая теорема.
Теорема: Существует и притом единственная функция 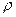 , удовлетворяющая определению длины отрезка.
, удовлетворяющая определению длины отрезка.
1. Доказательство существования.
Выбираем произвольно отрезок е.
На прямой l, содержащей данный отрезок 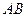 , создаем бесконечную шкалу, соседние точки деления которой – концы отрезка, равного (или конгруэнтного)
, создаем бесконечную шкалу, соседние точки деления которой – концы отрезка, равного (или конгруэнтного) 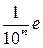 (рис.76).
(рис.76).

Рис. 76
Такую шкалу назовем разбиением прямой l ранга n. Для каждого целого неотрицательного n получаем конкретное разбиение прямой l ранга n.
Число всех отрезков разбиения ранга n, уместившихся на АВ, обозначим 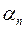 , а число всех отрезков этого разбиения, имеющих хотя бы одну общую точку с отрезком АВ, представим
, а число всех отрезков этого разбиения, имеющих хотя бы одну общую точку с отрезком АВ, представим 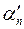 (на рис. 76
(на рис. 76 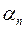 =7,
=7, 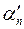 =9). Легко видеть, что
=9). Легко видеть, что 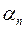 при любом n на две единицы меньше
при любом n на две единицы меньше 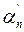 , иначе говоря
, иначе говоря 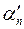 –
– 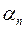 =2 при любом целом неотрицательном n. Умножив обе части этого равенства на 10- n, получаем равенство
=2 при любом целом неотрицательном n. Умножив обе части этого равенства на 10- n, получаем равенство 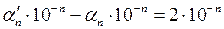 . Очевидно, что
. Очевидно, что 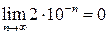 , что ведет к равенству
, что ведет к равенству 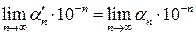 . Умножив последнее на е, получим
. Умножив последнее на е, получим  . Как нетрудно видеть,
. Как нетрудно видеть, 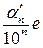 есть отрезок
есть отрезок 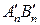 , содержащий АВ, а
, содержащий АВ, а 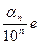 – отрезок
– отрезок 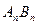 , содержащийся в АВ. Эти отрезки естественно назвать отрезками ранга n. Две последовательности отрезков
, содержащийся в АВ. Эти отрезки естественно назвать отрезками ранга n. Две последовательности отрезков 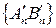 и
и 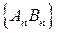 сходятся к одному и тому пределу, которым является отрезок АВ. Последовательности чисел
сходятся к одному и тому пределу, которым является отрезок АВ. Последовательности чисел 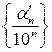 и
и 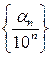 , связанных с отрезками последовательностей
, связанных с отрезками последовательностей 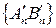 и
и 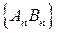 , как было отмечено выше, также сходятся к одному пределу, который является действительным положительным числом. Обозначим это число буквой
, как было отмечено выше, также сходятся к одному пределу, который является действительным положительным числом. Обозначим это число буквой 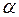 . Именно число
. Именно число 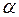 естественно поставить в соответствие отрезку АВ. Таким образом, появляется конструктивно определенное отображение множества отрезков в множество неотрицательных чисел, которое обозначим буквой
естественно поставить в соответствие отрезку АВ. Таким образом, появляется конструктивно определенное отображение множества отрезков в множество неотрицательных чисел, которое обозначим буквой 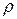 (ро). Для числа
(ро). Для числа 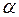 , о котором выше шла речь, становится возможным представление
, о котором выше шла речь, становится возможным представление 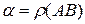 . Еще раз подчеркнем, что
. Еще раз подчеркнем, что 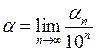 , где
, где  - число всех отрезков разбиения прямой АВ ранга n, принадлежащих отрезку АВ.
- число всех отрезков разбиения прямой АВ ранга n, принадлежащих отрезку АВ.
Теперь покажем, что  , поставленное в соответствие АВ, обладает свойствами 1, 2 и 3 из определения длины отрезка.
, поставленное в соответствие АВ, обладает свойствами 1, 2 и 3 из определения длины отрезка.
1) Итак, 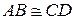 . Требуется доказать, что
. Требуется доказать, что 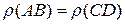 . Без потери общности можно считать, что оба отрезка лежат на одной прямой l, на которой задана «десятичная» шкала. При этом можно также считать, что точки А и С принадлежат одному отрезку ранга n. Этого можно добиться путем соответствующего перемещения CD на l. В это случае
. Без потери общности можно считать, что оба отрезка лежат на одной прямой l, на которой задана «десятичная» шкала. При этом можно также считать, что точки А и С принадлежат одному отрезку ранга n. Этого можно добиться путем соответствующего перемещения CD на l. В это случае 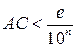 , а потому и
, а потому и 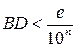 . Последнее означает, что точки B и D либо принадлежат одному отрезку ранга n, или принадлежат смежным отрезкам этого ранга (рис. 77).
. Последнее означает, что точки B и D либо принадлежат одному отрезку ранга n, или принадлежат смежным отрезкам этого ранга (рис. 77).
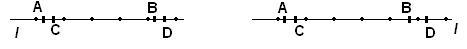
Рис. 77
Пусть число всех отрезков ранга n, содержащихся в АВ, есть 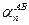 и соответственно
и соответственно 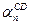 – число отрезков шкалы, содержащихся в CD. Очевидно, что в первом случае (левая часть рисунка 57)
– число отрезков шкалы, содержащихся в CD. Очевидно, что в первом случае (левая часть рисунка 57) 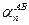 =
= 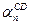 , а во втором
, а во втором 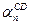 –
– 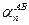 = 1(эта разность соответствует представленному на рисунке случаю). В общем случае |
= 1(эта разность соответствует представленному на рисунке случаю). В общем случае | 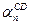 –
– 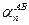 | ≤ 1. Отсюда
| ≤ 1. Отсюда 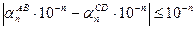 для любого целого неотрицательного n, а это означает, что
для любого целого неотрицательного n, а это означает, что 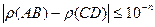 при всех допустимых n. Но
при всех допустимых n. Но 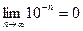 , следовательно
, следовательно 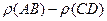 = 0 или
= 0 или 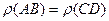 . Итак, условие 1 определения длины отрезка выполнено.
. Итак, условие 1 определения длины отрезка выполнено.
2) Пусть С – внутренняя точка АВ, а значит 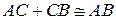 . В этом случае нужно доказать, что
. В этом случае нужно доказать, что  .
.
Снова АВ лежит на прямой l с десятичными шкалами рангов n. Для положения точки С на этой шкале снова характерны только два случая: С – общий конец смежных отрезков шкалы, С – внутренняя точка одного из отрезков шкалы, содержащихся в АВ (рис. 78).
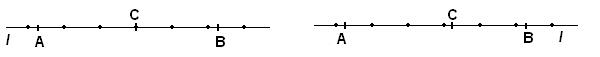
Рис. 78
Пусть 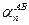 ,
, 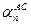 и
и 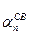 имеют тот же смысл, что и в предыдущих случаях. Для случая положения С на АВ, представленного в левой части рисунка, очевидно, что
имеют тот же смысл, что и в предыдущих случаях. Для случая положения С на АВ, представленного в левой части рисунка, очевидно, что 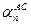 +
+ 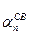 =
= 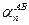 . В случае, отображенном в правой части рисунка
. В случае, отображенном в правой части рисунка 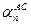 +
+ 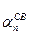 =
= 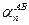 –1. Таким образом, в общем случае
–1. Таким образом, в общем случае 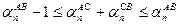 . Умножая все части двустороннего неравенства на 10-n и переходя к пределу, получим
. Умножая все части двустороннего неравенства на 10-n и переходя к пределу, получим  .
.
3) Рассмотрим фиксированный нами отрезок е. Именно его 10-n –ая часть использовалась для построения шкалы ранга n на прямой l. Сам отрезок е может располагаться на такой шкале либо так, как это изображено в левой части рисунка 79, либо так, как это представлено в его правой части.

Рис. 79
В первом случае, 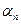 = 10-n , а во втором –
= 10-n , а во втором – 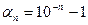 . Отсюда
. Отсюда 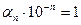 или
или 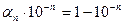 . Ясно, что и в первом и во втором случаях
. Ясно, что и в первом и во втором случаях 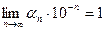 . Иначе говоря
. Иначе говоря 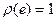 .
.
Таким образом, выполнено и третье условие определения длины.
2. Перейдем к доказательству единственности функции 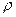 .
.
Пусть λ – какая-либо функция, заданная на множестве отрезков со значениями в R+, обладающая свойствами 1, 2 и 3 определения длины отрезка. Докажем, что λ совпадает с 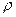 . Заметим, что единичный отрезок – отрезок е.
. Заметим, что единичный отрезок – отрезок е.
В силу условия 3 определения длины отрезка 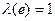 . Значит
. Значит 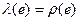 , отрезок е делим на 10n частей и эти части обозначим
, отрезок е делим на 10n частей и эти части обозначим 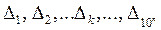 . В силу условия 1 определения длины
. В силу условия 1 определения длины 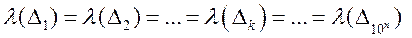 и
и 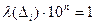 точно также как и
точно также как и 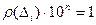 (i =1, 2, …, 10n). Отсюда
(i =1, 2, …, 10n). Отсюда 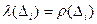 для любого соответствующего i.
для любого соответствующего i.
Пусть АВ – произвольный отрезок на l и MN – отрезок, составленный из всех 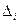 , входящих в АВ, а
, входящих в АВ, а 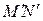 – минимальный отрезок, составленный из
– минимальный отрезок, составленный из 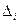 и содержащий АВ.
и содержащий АВ.
 и
и 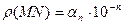 , значит
, значит 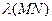 =
= 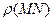 . Точно так же получаем
. Точно так же получаем 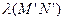 =
= 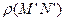 . Функции λ и
. Функции λ и 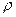 монотонно возрастают, поэтому
монотонно возрастают, поэтому 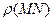 ≤
≤ 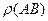 <
< 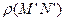 и
и 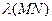 ≤
≤ 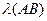 <
< 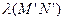 . Учитывая, что
. Учитывая, что 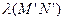 =
= 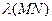 , получаем |
, получаем | 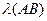 –
– 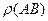 | ≤ 0, то есть
| ≤ 0, то есть 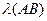 =
= 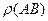 .
.
Таким образом, функции λ и 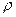 при фиксированном е совпадают.
при фиксированном е совпадают.
Теорема доказана полностью.
Замечание 1.
На первый взгляд, способ нахождения длины отрезка, основывающийся на доказанной теореме, не соответствует традиционно сложившемуся, когда на измеряемом отрезке последовательно сначала откладывается единичный отрезок е (если измеряемый больше или равен е), а затем, в случае возникновения остатка меньшего е, его десятая доля, то есть е 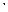 10-1, и так далее на (k+1)-ом шаге, при наличии остатка, на нем откладывается е
10-1, и так далее на (k+1)-ом шаге, при наличии остатка, на нем откладывается е 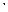 10-k. В результате длина отрезка представляется суммой (числовым рядом)
10-k. В результате длина отрезка представляется суммой (числовым рядом) 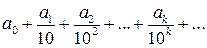 , где а0 – целое неотрицательное число, а все ai, где
, где а0 – целое неотрицательное число, а все ai, где 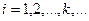 – целые числа из промежутка от 0 до 9. Такой ряд представляется десятичной дробью а0, а1а2…аk,…, которая может быть периодической или непериодической, а значит представляет либо рациональное, либо иррациональное число. На самом деле, практический прием измерения длины отрезка, всего лишь частный случай рассмотренного нами выше и связан лишь со специальным расположением измеряемого отрезка на десятичной шкале, которую мы задавали на прямой l. Один конец этого отрезка совмещается с нулевой точкой 0 прямой l.
– целые числа из промежутка от 0 до 9. Такой ряд представляется десятичной дробью а0, а1а2…аk,…, которая может быть периодической или непериодической, а значит представляет либо рациональное, либо иррациональное число. На самом деле, практический прием измерения длины отрезка, всего лишь частный случай рассмотренного нами выше и связан лишь со специальным расположением измеряемого отрезка на десятичной шкале, которую мы задавали на прямой l. Один конец этого отрезка совмещается с нулевой точкой 0 прямой l.
Замечание 2.
Длина отрезка зависит от выбора единичного отрезка е, при этом, если длина АВ, измеренная е 1, равна 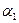 , а при его измерении единицей
, а при его измерении единицей 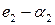 , то
, то 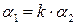 , где
, где 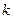 – длина е 1, измеренная е 2.
– длина е 1, измеренная е 2.
Замечание 3.
Начиная с А.Лежандра (1752-1833 гг.), отношение пропорциональности пар отрезков определяется как равенство двух отношений длин отрезков этих пар:  пропорциональна
пропорциональна 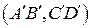 , если длины отрезков этих пар
, если длины отрезков этих пар 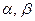 и
и 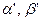 соответственно образуют пропорцию
соответственно образуют пропорцию  (или
(или 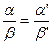 ).
).
В теории подобия фигур непосредственно используется, однако, не отношение отрезков, а пропорциональность пар отрезков (равенство отношений). При этом опираются на теорему «о пропорциональных отрезках», отложенных на сторонах угла, которая выступает геометрическим эквивалентом арифметическому определению пропорциональности пар отрезков.
Рассмотрим эту теорему.
Теорема: Пары отрезков 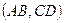 и
и 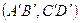 пропорциональны тогда и только тогда, когда
пропорциональны тогда и только тогда, когда 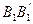 и
и 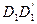 , соединяющие концы отрезков
, соединяющие концы отрезков 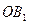 и
и 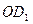 ,
, 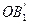 и
и 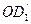 , равных (конгруэнтных) соответственно AB и CD,
, равных (конгруэнтных) соответственно AB и CD, 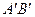 и
и 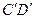 и отложенных от вершины О
и отложенных от вершины О  на его сторонах h и k соответственно, параллельны.
на его сторонах h и k соответственно, параллельны.
1. Пусть прямые 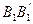 и
и 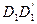 параллельны. Докажем, что
параллельны. Докажем, что 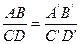 .
.
Рассматриваем два случая:
1) АВ и CD соизмеримы
2) АВ и CD несоизмеримы
Случай 1. Отметим, что в этом случае соизмеримы и 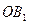 и
и 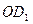 (рис.80).
(рис.80).
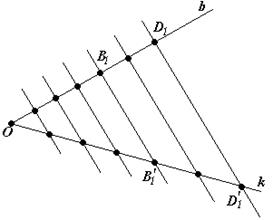
Рис. 80
Пусть е – единичный отрезок, представляющий m -ю часть отрезка АВ, тогда АВ = е 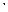 m и в рассматриваемом случае CD = e
m и в рассматриваемом случае CD = e 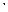 n. Тогда и
n. Тогда и 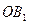 = e
= e 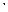 m и
m и 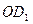 = e
= e 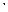 n. Делим
n. Делим 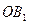 и
и 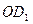 на m и n равных частей (каждая часть равна е). Проведя через точки деления прямые, параллельные
на m и n равных частей (каждая часть равна е). Проведя через точки деления прямые, параллельные 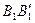 и
и 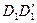 , разобьем и отрезки
, разобьем и отрезки 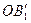 и
и 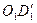 на m и n равных частей соответственно. Поэтому
на m и n равных частей соответственно. Поэтому 
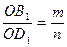 и
и 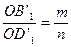 . Таким образом, получаем пропорцию
. Таким образом, получаем пропорцию 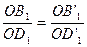 , а отсюда и
, а отсюда и 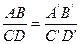 .
.
Случай 2. АВ и CD несоизмеримы. В этом случае несоизмеримы и 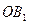 и
и 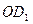 (рис.81).
(рис.81).
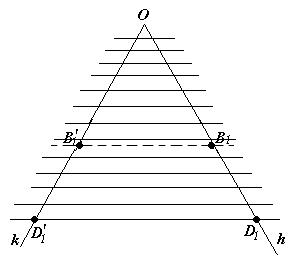
Рис. 81
Делим отрезок 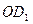 на 10n равных частей (n = 1, 2, …). При этом
на 10n равных частей (n = 1, 2, …). При этом 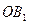 не делится на равные части ни при одном значении n.
не делится на равные части ни при одном значении n.
Пусть n = 1, тогда 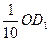 укладывается на
укладывается на 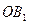 m 1 с остатком, меньшим
m 1 с остатком, меньшим 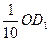 , таким образом
, таким образом 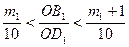 . По теореме Фалеса и
. По теореме Фалеса и 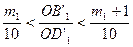 . Далее делим
. Далее делим 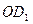 на 102. Такие же рассуждения приводят нас к неравенствам
на 102. Такие же рассуждения приводят нас к неравенствам 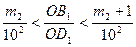 и
и 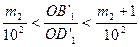 .
.
На р -м шаге имеем два неравенства:
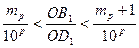 и
и 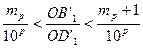 и так далее для любого натурального n. Получаем
и так далее для любого натурального n. Получаем 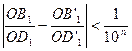 . Так как
. Так как 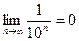 , то
, то 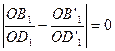 , что возможно лишь при условии равенства
, что возможно лишь при условии равенства 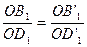 или соответственно
или соответственно 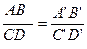 .
.
Итак, достаточность условия теоремы доказана.
Теперь обратное.
2. Пусть 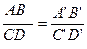 , а значит и
, а значит и 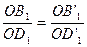 . Доказать, что
. Доказать, что 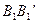 ║
║ 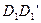 (рис.82).
(рис.82).
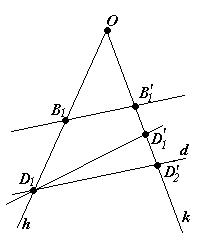
Рис. 82
Проведем через D 1 прямую d, параллельную 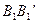 , и пусть она пересекает k в точке
, и пусть она пересекает k в точке 
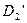 . Так как по доказанному выше из
. Так как по доказанному выше из 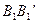 ║
║ 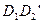 следует
следует 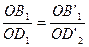 , то получаем две пропорции: та что представлена в условии утверждения, то есть
, то получаем две пропорции: та что представлена в условии утверждения, то есть 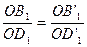 , и полученная нами для отрезков
, и полученная нами для отрезков 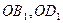 и
и  . Отсюда получаем:
. Отсюда получаем: 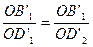 , что возможно лишь при условии равенства (конгруэнтности) отрезков
, что возможно лишь при условии равенства (конгруэнтности) отрезков 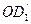 и
и 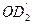 . В силу аксиом третьей группы (аксиом конгруэнтности) это возможно лишь при условии совпадения точек
. В силу аксиом третьей группы (аксиом конгруэнтности) это возможно лишь при условии совпадения точек 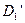 и
и 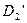 . Последнее означает совпадение прямых
. Последнее означает совпадение прямых 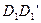 и
и 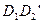 . Таким образом,
. Таким образом, 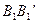 ║
║ 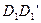 .
.
2º. Площадь плоской фигуры.
Рассматриваются ограниченные фигуры и именно для таких фигур вводится понятие площади. По форме это определение совпадает с определением длины отрезка, как и в этом случае, площадь – функция, задаваемая на множестве фигур, значениями которой являются положительные действительные числа.
Определение 1: Будем говорить, что фигура F разбита на составляющие фигуры F 1 и F 2, если: каждая точка F является точкой либо фигуры F 1, либо фигуры F 2 и наоборот, всякая точка F 1 или F 2 есть точка фигуры F; F 1 и F 2 не имеют общих точек, кроме точек границы этих фигур.
Примеры разбиения фигуры на составляющие приведены на рис. 83.
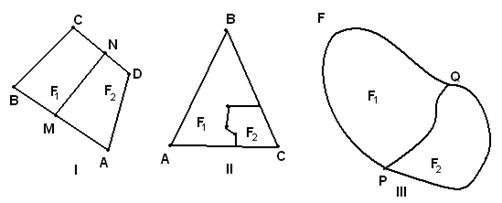
Рис. 83
В случае I четырехугольник ABCD разбит на составляющие отрезком MN, в случае II треугольник ABC разбит на составляющие фигуры ломаной линией, а в случае III фигура F разбита на F 1 и F 2 линией, соединяющей точки P и Q, принадлежащие границе фигуры F.
Определение 2: Площадью плоской фигуры 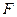 называют действительное неотрицательное число, поставленное фигуре
называют действительное неотрицательное число, поставленное фигуре 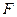 в соответствие так, что при этом:
в соответствие так, что при этом:
1) равные фигуры имеют равные площади;
2) если фигура разбита на две составляющие фигуры, то ее площадь равна сумме составляющих фигур;
3) площадь квадрата со стороной, длина которой равна 1, равна 1.
Основная задача – указать функцию, определенную на множестве фигур, значения которой – неотрицательные действительные числа, удовлетворяющие условиям 1, 2 и 3.
Следует заметить, что в отличие от длины отрезка площадь плоской фигуры определена не на множестве всех возможных плоских фигур, а только на множестве так называемых квадрируемых фигур, то есть, прежде всего, фигур ограниченных, представляющих замкнутые области. В общем случае, рассматривают две последовательности простых (или даже выпуклых) многоугольников, из которых первая – последовательность многоугольников, вложенных в фигуру F, а вторая – содержащих в себе эту фигуру. Если 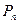 – члены первой последовательности, а
– члены первой последовательности, а 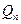 – второй, то
– второй, то 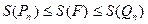 для любого натурального n. F квадрируема, если
для любого натурального n. F квадрируема, если 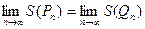 . Именно этот общий предел и принимается за значение функции S(F). Только с квадрируемыми фигурами и имеет дело теория площадей плоских фигур. Определение квадрируемой фигуры показывает, что в нем используется понятие простого многоугольника. Поэтому возникает задачa №1 о построении соответствующей функции-площади на множестве простых многоугольников. Решение этой задачи приводит нас к определению функции S(F) на множестве треугольников, а эта последняя базируется на определении S(F) на множестве прямоугольников. Таким образом, возникает следующая последовательность в решении общей задачи:
. Именно этот общий предел и принимается за значение функции S(F). Только с квадрируемыми фигурами и имеет дело теория площадей плоских фигур. Определение квадрируемой фигуры показывает, что в нем используется понятие простого многоугольника. Поэтому возникает задачa №1 о построении соответствующей функции-площади на множестве простых многоугольников. Решение этой задачи приводит нас к определению функции S(F) на множестве треугольников, а эта последняя базируется на определении S(F) на множестве прямоугольников. Таким образом, возникает следующая последовательность в решении общей задачи:
1) площадь прямоугольника;
2) площадь треугольника;
3) площадь выпуклого многоугольника;
4) площадь квадрируемой фигуры.
Рассмотрим в указанной последовательности эти случаи определения площади выпуклого многоугольника.
1. Площадь прямоугольника P со смежными сторонами a и b.
a) P есть квадрат, тогда a = b. Пусть Е – квадрат со стороной, равной 1 и сторона квадрата P имеет длину 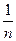 . Тогда S(E) = S(P)
. Тогда S(E) = S(P) 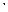 n2. Отсюда
n2. Отсюда 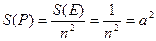 .
.
b) Р – прямоугольник, смежные стороны которого имеют длины a и b соответственно.
1) a и b – числа рациональные. Представляем эти числа дробями со знаменателем n, то есть 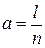 и
и 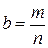 . Делим стороны прямоугольника соответственно на l и m частей и через точки деления проводим прямые, параллельные сторонам прямоугольника. Прямоугольник оказывается разделенным на lm квадратов, площадь которых равна
. Делим стороны прямоугольника соответственно на l и m частей и через точки деления проводим прямые, параллельные сторонам прямоугольника. Прямоугольник оказывается разделенным на lm квадратов, площадь которых равна 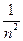 (сторона каждого квадрата имеет длину
(сторона каждого квадрата имеет длину 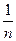 ). Таким образом, площадь прямоугольника Р равна
). Таким образом, площадь прямоугольника Р равна 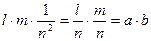 , то есть S(P) = ab.
, то есть S(P) = ab.
2) Хотя бы одно из чисел a и b – число иррациональное. Для a и b существуют рациональные приближения как «по недостатку», так и «по избытку». Последовательности этих приближений обозначаем соответственно 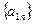 ,
,  и
и 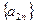 ,
,  .
. 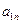 и
и 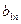 – длины смежных сторон прямоугольников, входящих в данный прямоугольник Р, а
– длины смежных сторон прямоугольников, входящих в данный прямоугольник Р, а 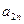 и
и 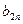 – длины смежных сторон прямоугольников, содержащих в себе Р (рис. 84).
– длины смежных сторон прямоугольников, содержащих в себе Р (рис. 84).
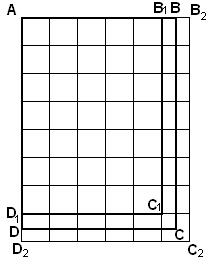
Рис. 84
ABCD – прямоугольник Р, со сторонами a и b. 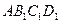 – прямоугольник со сторонами
– прямоугольник со сторонами 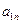 и
и 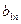 , входящий в Р.
, входящий в Р. 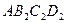 – прямоугольник со сторонами
– прямоугольник со сторонами 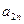 и
и 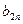 , содержащий Р.
, содержащий Р.
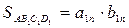 , коротко обозначим ее
, коротко обозначим ее 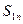 ;
; 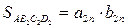 , которую обозначим
, которую обозначим 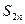 .
.
Очевидно, что  . Площади прямоугольников ABCD,
. Площади прямоугольников ABCD, 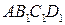 и
и 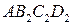 очевидно связаны неравенствами
очевидно связаны неравенствами 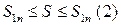 .
.
Так как 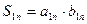 , а
, а 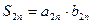 , то неравенство (1) предстанет в виде
, то неравенство (1) предстанет в виде 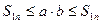 . Сопоставляя последнее с неравенством (2) получаем
. Сопоставляя последнее с неравенством (2) получаем 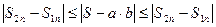 , то есть
, то есть 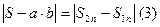 . Но для любого наперед заданного
. Но для любого наперед заданного 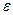 >0 найдется такое n (
>0 найдется такое n (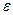 ) такое, что как только n > n (
) такое, что как только n > n (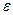 )
) 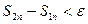 . Подставляя это в равенство (3) получаем: неравенство
. Подставляя это в равенство (3) получаем: неравенство 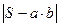 <
< 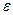 при любом наперед заданном
при любом наперед заданном 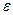 . Это возможно лишь для числа 0. Таким образом
. Это возможно лишь для числа 0. Таким образом 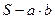 =0 или
=0 или 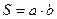 .
.
Вывод: Площадь прямоугольника с длинами смежных сторон a и b равна произведению  при любых положительных действительных a и b.
при любых положительных действительных a и b.
2. Площадь параллелограмма.
Путь ABCD – параллелограмм, отличный от прямоугольника (рис.85).
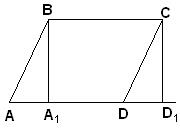
Рис. 85
Из смежных вершин В и С опускаем на AD перпендикуляры. Пусть A 1 и D 1 – точки их пересечения с AD.
Четырехугольник 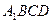 – общая часть данного параллелограмма и прямоугольника
– общая часть данного параллелограмма и прямоугольника 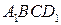 . Треугольники
. Треугольники  и
и 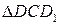 конгруэнтны (равны).
конгруэнтны (равны).
В силу свойства 1 определения площади фигуры 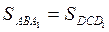 , кроме того
, кроме того 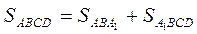 и
и 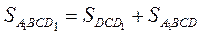 (в силу свойства 2 определения площади). Правые части этих равенств равны, значит равны и их левые части, то есть имеем
(в силу свойства 2 определения площади). Правые части этих равенств равны, значит равны и их левые части, то есть имеем 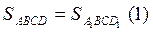 . ВА 1 – не только сторона прямоугольника A 1 BCD 1, но и высота данного параллелограмма, обозначим ее ha. Сторона ВС параллелограмма ABCD является и стороной прямоугольника A 1 BCD 1, обозначим ее а. При выбранных обозначениях
. ВА 1 – не только сторона прямоугольника A 1 BCD 1, но и высота данного параллелограмма, обозначим ее ha. Сторона ВС параллелограмма ABCD является и стороной прямоугольника A 1 BCD 1, обозначим ее а. При выбранных обозначениях 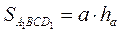 . В силу равенства (1) и
. В силу равенства (1) и
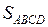 = а . ha.
= а . ha.



 10-7 части парижского меридиана (или 1553164,13 длины волны красной линии спектра кадмия при определенных условиях относительной влажности и состава воздуха, его температуры и давления, ускорения тяжести и других факторах). Соответствующие его десятичные доли получили названия: дециметр, сантиметр, миллиметр и т.д. Отрезки, кратные метру в десятичной системе также получают специальные названия, например, километр.
10-7 части парижского меридиана (или 1553164,13 длины волны красной линии спектра кадмия при определенных условиях относительной влажности и состава воздуха, его температуры и давления, ускорения тяжести и других факторах). Соответствующие его десятичные доли получили названия: дециметр, сантиметр, миллиметр и т.д. Отрезки, кратные метру в десятичной системе также получают специальные названия, например, километр.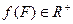 ;
;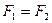 , то
, то 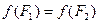 ;
;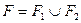 и
и 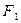 и
и 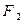 не имеют общих внутренних точек, то
не имеют общих внутренних точек, то 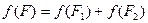 ;
;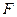 такая, что
такая, что  .
.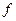 – отображение множества фигур на множество
– отображение множества фигур на множество 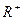 положительных действительных чисел,
положительных действительных чисел, 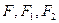 – фигуры, иначе элементы множества фигур. Так как в общем виде, то есть вне зависимости от типа фигур, такая функция, как оказалось, не может быть построена, то рассматривается построение отдельных функций, определяемых на классах конкретных фигур одного вида, если, конечно, в рассматриваемом случае множество фигур допускает его разбиение на классы однотипных фигур. Так, например, для множества отрезков прямой речь может идти только об одном (неделимом) классе фигур, представляющем все множество отрезков пространства. Для множества плоских или пространственных фигур такое разбиение на классы возможно, например, на множество прямоугольников, множество параллелограммов, множество треугольников и т.д. и т.п. Второе, третье и четвертое свойства понятий длины, площади и объема называют соответственно свойствами инвариантности, аддитивности и нормированности меры.
– фигуры, иначе элементы множества фигур. Так как в общем виде, то есть вне зависимости от типа фигур, такая функция, как оказалось, не может быть построена, то рассматривается построение отдельных функций, определяемых на классах конкретных фигур одного вида, если, конечно, в рассматриваемом случае множество фигур допускает его разбиение на классы однотипных фигур. Так, например, для множества отрезков прямой речь может идти только об одном (неделимом) классе фигур, представляющем все множество отрезков пространства. Для множества плоских или пространственных фигур такое разбиение на классы возможно, например, на множество прямоугольников, множество параллелограммов, множество треугольников и т.д. и т.п. Второе, третье и четвертое свойства понятий длины, площади и объема называют соответственно свойствами инвариантности, аддитивности и нормированности меры.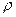 (ро), то длина отрезка
(ро), то длина отрезка 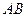 может быть записана как
может быть записана как 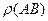 . Алгоритм нахождения длины отрезка
. Алгоритм нахождения длины отрезка 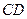 найдется такое натуральное
найдется такое натуральное 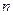 , что
, что 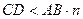 , где
, где
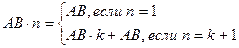
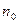 , для которого
, для которого 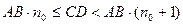 .
.
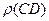 будет представлено в виде цепной дроби. Например, если
будет представлено в виде цепной дроби. Например, если 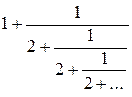 .
.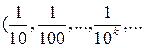 доли единичного отрезка).
доли единичного отрезка).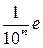 (рис.76).
(рис.76).
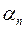 , а число всех отрезков этого разбиения, имеющих хотя бы одну общую точку с отрезком АВ, представим
, а число всех отрезков этого разбиения, имеющих хотя бы одну общую точку с отрезком АВ, представим 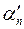 (на рис. 76
(на рис. 76 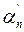 , иначе говоря
, иначе говоря 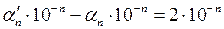 . Очевидно, что
. Очевидно, что 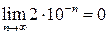 , что ведет к равенству
, что ведет к равенству 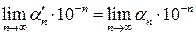 . Умножив последнее на е, получим
. Умножив последнее на е, получим  . Как нетрудно видеть,
. Как нетрудно видеть, 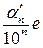 есть отрезок
есть отрезок 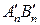 , содержащий АВ, а
, содержащий АВ, а 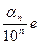 – отрезок
– отрезок 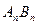 , содержащийся в АВ. Эти отрезки естественно назвать отрезками ранга n. Две последовательности отрезков
, содержащийся в АВ. Эти отрезки естественно назвать отрезками ранга n. Две последовательности отрезков 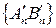 и
и 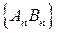 сходятся к одному и тому пределу, которым является отрезок АВ. Последовательности чисел
сходятся к одному и тому пределу, которым является отрезок АВ. Последовательности чисел 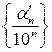 и
и 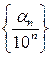 , связанных с отрезками последовательностей
, связанных с отрезками последовательностей 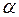 . Именно число
. Именно число 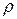 (ро). Для числа
(ро). Для числа 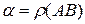 . Еще раз подчеркнем, что
. Еще раз подчеркнем, что 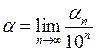 , где
, где  - число всех отрезков разбиения прямой АВ ранга n, принадлежащих отрезку АВ.
- число всех отрезков разбиения прямой АВ ранга n, принадлежащих отрезку АВ. , поставленное в соответствие АВ, обладает свойствами 1, 2 и 3 из определения длины отрезка.
, поставленное в соответствие АВ, обладает свойствами 1, 2 и 3 из определения длины отрезка.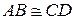 . Требуется доказать, что
. Требуется доказать, что 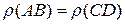 . Без потери общности можно считать, что оба отрезка лежат на одной прямой l, на которой задана «десятичная» шкала. При этом можно также считать, что точки А и С принадлежат одному отрезку ранга n. Этого можно добиться путем соответствующего перемещения CD на l. В это случае
. Без потери общности можно считать, что оба отрезка лежат на одной прямой l, на которой задана «десятичная» шкала. При этом можно также считать, что точки А и С принадлежат одному отрезку ранга n. Этого можно добиться путем соответствующего перемещения CD на l. В это случае 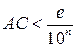 , а потому и
, а потому и 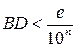 . Последнее означает, что точки B и D либо принадлежат одному отрезку ранга n, или принадлежат смежным отрезкам этого ранга (рис. 77).
. Последнее означает, что точки B и D либо принадлежат одному отрезку ранга n, или принадлежат смежным отрезкам этого ранга (рис. 77).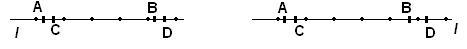
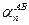 и соответственно
и соответственно 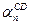 – число отрезков шкалы, содержащихся в CD. Очевидно, что в первом случае (левая часть рисунка 57)
– число отрезков шкалы, содержащихся в CD. Очевидно, что в первом случае (левая часть рисунка 57) 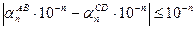 для любого целого неотрицательного n, а это означает, что
для любого целого неотрицательного n, а это означает, что 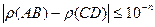 при всех допустимых n. Но
при всех допустимых n. Но 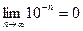 , следовательно
, следовательно 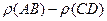 = 0 или
= 0 или 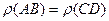 . Итак, условие 1 определения длины отрезка выполнено.
. Итак, условие 1 определения длины отрезка выполнено.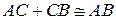 . В этом случае нужно доказать, что
. В этом случае нужно доказать, что  .
.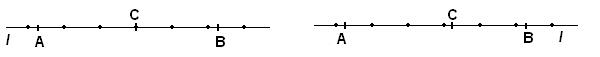
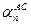 и
и 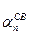 имеют тот же смысл, что и в предыдущих случаях. Для случая положения С на АВ, представленного в левой части рисунка, очевидно, что
имеют тот же смысл, что и в предыдущих случаях. Для случая положения С на АВ, представленного в левой части рисунка, очевидно, что 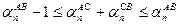 . Умножая все части двустороннего неравенства на 10-n и переходя к пределу, получим
. Умножая все части двустороннего неравенства на 10-n и переходя к пределу, получим  .
.
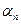 = 10-n , а во втором –
= 10-n , а во втором – 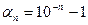 . Отсюда
. Отсюда 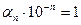 или
или 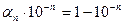 . Ясно, что и в первом и во втором случаях
. Ясно, что и в первом и во втором случаях 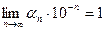 . Иначе говоря
. Иначе говоря 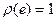 .
.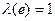 . Значит
. Значит 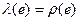 , отрезок е делим на 10n частей и эти части обозначим
, отрезок е делим на 10n частей и эти части обозначим 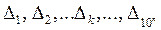 . В силу условия 1 определения длины
. В силу условия 1 определения длины 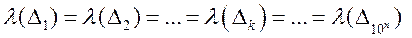 и
и 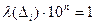 точно также как и
точно также как и 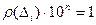 (i =1, 2, …, 10n). Отсюда
(i =1, 2, …, 10n). Отсюда 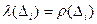 для любого соответствующего i.
для любого соответствующего i.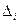 , входящих в АВ, а
, входящих в АВ, а 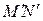 – минимальный отрезок, составленный из
– минимальный отрезок, составленный из  и
и 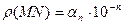 , значит
, значит 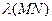 =
= 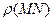 . Точно так же получаем
. Точно так же получаем 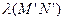 =
= 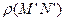 . Функции λ и
. Функции λ и 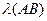 <
< 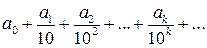 , где а0 – целое неотрицательное число, а все ai, где
, где а0 – целое неотрицательное число, а все ai, где 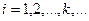 – целые числа из промежутка от 0 до 9. Такой ряд представляется десятичной дробью а0, а1а2…аk,…, которая может быть периодической или непериодической, а значит представляет либо рациональное, либо иррациональное число. На самом деле, практический прием измерения длины отрезка, всего лишь частный случай рассмотренного нами выше и связан лишь со специальным расположением измеряемого отрезка на десятичной шкале, которую мы задавали на прямой l. Один конец этого отрезка совмещается с нулевой точкой 0 прямой l.
– целые числа из промежутка от 0 до 9. Такой ряд представляется десятичной дробью а0, а1а2…аk,…, которая может быть периодической или непериодической, а значит представляет либо рациональное, либо иррациональное число. На самом деле, практический прием измерения длины отрезка, всего лишь частный случай рассмотренного нами выше и связан лишь со специальным расположением измеряемого отрезка на десятичной шкале, которую мы задавали на прямой l. Один конец этого отрезка совмещается с нулевой точкой 0 прямой l.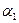 , а при его измерении единицей
, а при его измерении единицей 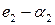 , то
, то 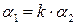 , где
, где 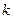 – длина е 1, измеренная е 2.
– длина е 1, измеренная е 2. пропорциональна
пропорциональна 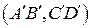 , если длины отрезков этих пар
, если длины отрезков этих пар 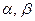 и
и 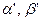 соответственно образуют пропорцию
соответственно образуют пропорцию  (или
(или 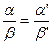 ).
).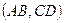 и
и 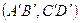 пропорциональны тогда и только тогда, когда
пропорциональны тогда и только тогда, когда 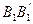 и
и 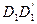 , соединяющие концы отрезков
, соединяющие концы отрезков 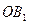 и
и 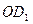 ,
, 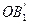 и
и 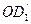 , равных (конгруэнтных) соответственно AB и CD,
, равных (конгруэнтных) соответственно AB и CD, 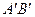 и
и 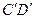 и отложенных от вершины О
и отложенных от вершины О  на его сторонах h и k соответственно, параллельны.
на его сторонах h и k соответственно, параллельны.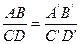 .
.
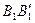 и
и 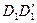 , разобьем и отрезки
, разобьем и отрезки 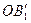 и
и 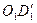 на m и n равных частей соответственно. Поэтому
на m и n равных частей соответственно. Поэтому 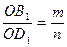 и
и 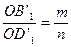 . Таким образом, получаем пропорцию
. Таким образом, получаем пропорцию 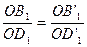 , а отсюда и
, а отсюда и 
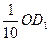 укладывается на
укладывается на 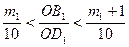 . По теореме Фалеса и
. По теореме Фалеса и 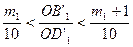 . Далее делим
. Далее делим 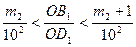 и
и 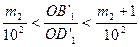 .
.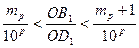 и
и 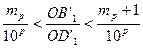 и так далее для любого натурального n. Получаем
и так далее для любого натурального n. Получаем 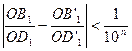 . Так как
. Так как 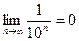 , то
, то 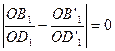 , что возможно лишь при условии равенства
, что возможно лишь при условии равенства 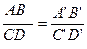 .
.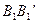 ║
║ 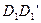 (рис.82).
(рис.82).
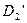 . Так как по доказанному выше из
. Так как по доказанному выше из 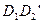 следует
следует 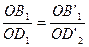 , то получаем две пропорции: та что представлена в условии утверждения, то есть
, то получаем две пропорции: та что представлена в условии утверждения, то есть 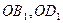 и
и  . Отсюда получаем:
. Отсюда получаем: 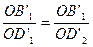 , что возможно лишь при условии равенства (конгруэнтности) отрезков
, что возможно лишь при условии равенства (конгруэнтности) отрезков 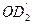 . В силу аксиом третьей группы (аксиом конгруэнтности) это возможно лишь при условии совпадения точек
. В силу аксиом третьей группы (аксиом конгруэнтности) это возможно лишь при условии совпадения точек 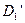 и
и 
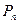 – члены первой последовательности, а
– члены первой последовательности, а 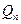 – второй, то
– второй, то 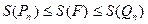 для любого натурального n. F квадрируема, если
для любого натурального n. F квадрируема, если 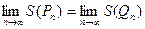 . Именно этот общий предел и принимается за значение функции S(F). Только с квадрируемыми фигурами и имеет дело теория площадей плоских фигур. Определение квадрируемой фигуры показывает, что в нем используется понятие простого многоугольника. Поэтому возникает задачa №1 о построении соответствующей функции-площади на множестве простых многоугольников. Решение этой задачи приводит нас к определению функции S(F) на множестве треугольников, а эта последняя базируется на определении S(F) на множестве прямоугольников. Таким образом, возникает следующая последовательность в решении общей задачи:
. Именно этот общий предел и принимается за значение функции S(F). Только с квадрируемыми фигурами и имеет дело теория площадей плоских фигур. Определение квадрируемой фигуры показывает, что в нем используется понятие простого многоугольника. Поэтому возникает задачa №1 о построении соответствующей функции-площади на множестве простых многоугольников. Решение этой задачи приводит нас к определению функции S(F) на множестве треугольников, а эта последняя базируется на определении S(F) на множестве прямоугольников. Таким образом, возникает следующая последовательность в решении общей задачи: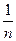 . Тогда S(E) = S(P)
. Тогда S(E) = S(P) 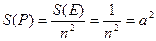 .
.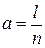 и
и 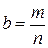 . Делим стороны прямоугольника соответственно на l и m частей и через точки деления проводим прямые, параллельные сторонам прямоугольника. Прямоугольник оказывается разделенным на lm квадратов, площадь которых равна
. Делим стороны прямоугольника соответственно на l и m частей и через точки деления проводим прямые, параллельные сторонам прямоугольника. Прямоугольник оказывается разделенным на lm квадратов, площадь которых равна 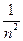 (сторона каждого квадрата имеет длину
(сторона каждого квадрата имеет длину 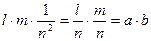 , то есть S(P) = ab.
, то есть S(P) = ab.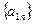 ,
,  и
и 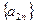 ,
,  .
. 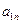 и
и 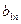 – длины смежных сторон прямоугольников, входящих в данный прямоугольник Р, а
– длины смежных сторон прямоугольников, входящих в данный прямоугольник Р, а 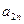 и
и 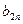 – длины смежных сторон прямоугольников, содержащих в себе Р (рис. 84).
– длины смежных сторон прямоугольников, содержащих в себе Р (рис. 84).
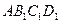 – прямоугольник со сторонами
– прямоугольник со сторонами 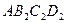 – прямоугольник со сторонами
– прямоугольник со сторонами 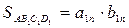 , коротко обозначим ее
, коротко обозначим ее 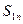 ;
; 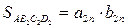 , которую обозначим
, которую обозначим 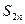 .
. . Площади прямоугольников ABCD,
. Площади прямоугольников ABCD, 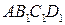 и
и 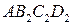 очевидно связаны неравенствами
очевидно связаны неравенствами 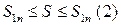 .
.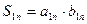 , а
, а 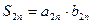 , то неравенство (1) предстанет в виде
, то неравенство (1) предстанет в виде 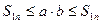 . Сопоставляя последнее с неравенством (2) получаем
. Сопоставляя последнее с неравенством (2) получаем 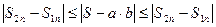 , то есть
, то есть 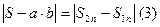 . Но для любого наперед заданного
. Но для любого наперед заданного 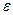 >0 найдется такое n (
>0 найдется такое n (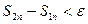 . Подставляя это в равенство (3) получаем: неравенство
. Подставляя это в равенство (3) получаем: неравенство 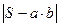 <
< 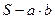 =0 или
=0 или 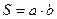 .
. при любых положительных действительных a и b.
при любых положительных действительных a и b.
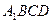 – общая часть данного параллелограмма и прямоугольника
– общая часть данного параллелограмма и прямоугольника 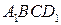 . Треугольники
. Треугольники  и
и 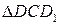 конгруэнтны (равны).
конгруэнтны (равны).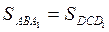 , кроме того
, кроме того 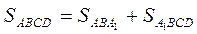 и
и 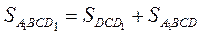 (в силу свойства 2 определения площади). Правые части этих равенств равны, значит равны и их левые части, то есть имеем
(в силу свойства 2 определения площади). Правые части этих равенств равны, значит равны и их левые части, то есть имеем 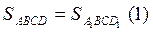 . ВА 1 – не только сторона прямоугольника A 1 BCD 1, но и высота данного параллелограмма, обозначим ее ha. Сторона ВС параллелограмма ABCD является и стороной прямоугольника A 1 BCD 1, обозначим ее а. При выбранных обозначениях
. ВА 1 – не только сторона прямоугольника A 1 BCD 1, но и высота данного параллелограмма, обозначим ее ha. Сторона ВС параллелограмма ABCD является и стороной прямоугольника A 1 BCD 1, обозначим ее а. При выбранных обозначениях 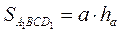 . В силу равенства (1) и
. В силу равенства (1) и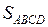 = а . ha.
= а . ha.


