1º. Понятия о многоугольниках и многогранниках, так или иначе, связываются с понятием о ломаной линии. Поэтому обратимся, прежде всего, к нему. Самое общее представление о ломаной линии – это определенная совокупность отрезков, у которых конец одного является началом другого. Такому представлению будет соответствовать следующее определение.
Определение 1: Ломаной линией с вершинами А 1, А 2, …, А n называют фигуру, состоящую из всех отрезков A i A i+1, где i = 1, 2,…, n -1.
А i, как уже отмечено в определении – вершины ломаной, A i A i+1 – звенья ломаной линии.
В самом общем случае A i расположены как угодно, то есть могут все или частично совпадать, все или частично принадлежать одной плоскости. С точки зрения элементарной геометрии вполне достаточно, чтобы все вершины принадлежали одной плоскости, но при этом никакие три последовательные не принадлежали одной прямой. Именно о таких ломаных линиях мы сейчас и говорим.
Но даже в этом случае множество ломаных линий значительно шире того их класса, с которым имеют дело в элементарной геометрии. Мы ограничиваемся лишь теми, для которых выполняются условия:
1. никакая вершина не может быть концом более чем двух звеньев;
2. никакая вершина не может быть внутренней точкой никакого звена;
3. никакие два звена не могут иметь общих внутренних точек
(рис. 65).
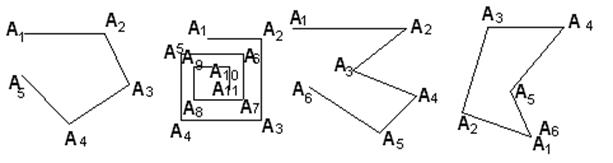
Рис. 65
Такие линии называют простыми ломаными линиями. В отличие от этих случаев остальные плоские ломаные линии называют звездчатыми (рис. 66).
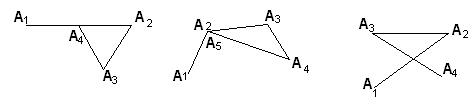
Рис. 66
Простые ломаные линии делят на выпуклые и невыпуклые.
На рисунке 67 слева – выпуклая линия, справа – невыпуклая.
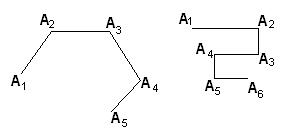
Рис. 67
Ломаная линия – выпуклая, если для любой прямой AiAi+1, содержащей соседние вершины Ai и Ai+1 все ее остальные вершины расположены в плоскости по одну сторону от прямой A i A i+1.
2º. Многоугольник – частный случай ломаной линии, когда ее первая вершина А 1 совпадает с n -ой вершиной A n. Смотрите, например, правую часть рисунка 65. У ломаной А 1 А 2 А 3 А 4 А 5 А 6 первая и шестая вершины – одна и та же точка. Таким образом, многоугольник есть замкнутая ломаная линия. Вообще говоря, эта линия необязательно должна быть плоской, но в евклидовой геометрии многоугольник – плоская линия.
Классификация многоугольников соответствует прежде всего классификации ломаных линий: первое деление – на простые и звездчатые, и далее – на выпуклые и невыпуклые (рис. 68).
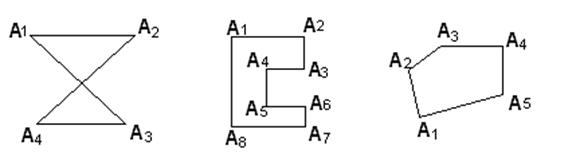
Рис. 68
Простые многоугольники делятся на выпуклые и невыпуклые. На рисунке 68 справа – выпуклый многоугольник, по середине – простой невыпуклый.
Отметим еще, что в случае, когда ломаная линия представляет многоугольник, ее звенья называют сторонами многоугольника. Если ломаная линия А 1 А 2… А n A n+1 представляет собой многоугольник, то есть вершины A 1 и A n+1 совпадают, то в обозначении многоугольника опускают обозначение конца An+1 ломаной линии, так что, например, вместо записи А 1 А 2 А 3 А 4 А 5 А 6 (рис. 65) используют запись А 1 А 2 А 3 А 4 А 5. При этом лишь следует впереди такого обозначения многоугольника написать слово «многоугольник».
Для простого многоугольника вводятся понятия внутреннего и внешнего углов. Соседними вершинами для вершины A i являются вершины A i-1 и A i+1. Поэтому со сторонами A i-1 A i и A i A i+1 связаны лучи 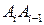 и A i A i+1. Эти лучи образуют угол, который можно обозначить как
и A i A i+1. Эти лучи образуют угол, который можно обозначить как 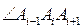 . Этот угол называют внутренним углом многоугольника
. Этот угол называют внутренним углом многоугольника
А 1… А i-1 A i A i+1... A n (рис. 69).
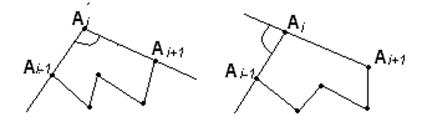
Рис. 69
Угол, образованный лучом A i A i-1 и лучом 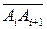 ,противоположным лучу A i A i+1, называют внешним углом многоугольника (рис. 49, его правая часть).
,противоположным лучу A i A i+1, называют внешним углом многоугольника (рис. 49, его правая часть).
Для всякого простого многоугольника точки плоскости, не принадлежащие многоугольнику, можно разделить на два класса, две области. Прежде всего, для любых двух точек плоскости, не принадлежащих многоугольнику, имеет место одно из двух: либо существует ломаная линия, соединяющая эти точки и не имеющая с многоугольником общих точек, либо любая такая ломаная пересекает многоугольник. В первом случае говорят, что точки принадлежат одной области, а во втором – принадлежат разным областям. Доказав существование точек принадлежащих разным областям, можно ввести понятия внешней и внутренней области для многоугольника.
Область относительно простого многоугольника называется его внутренней областью, если любая прямая, проходящая через любую ее точку пересекает многоугольник (имеет с ним общие точки).
Область относительно простого многоугольника называется его внешней областью, если существует точка области, для которой найдется прямая, проходящая через нее и не имеющая общих точек с многоугольником.
На рисунке 70 представлены точки внутренней и внешней областей многоугольника А 1 А 2 А 3 А 4 А 5: M – точка внутренней области, 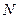 – точка внешней области.
– точка внешней области.
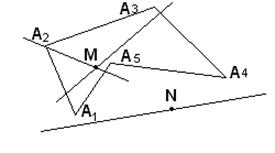
Рис. 70
Обоснование деления точек плоскости на две области проводить не будем вследствие значительного объема этой работы. Интересующийся читатель может обратиться к «Основаниям геометрии» Д.Гильберта, где в разделе «Примечания» приведено полное решение этой задачи.
В случае простых многоугольников часто их рассматривают совместно с внутренней их областью, называя именно такое объединение многоугольником. Таким образом, термин «многоугольник» используется для обозначения двух разных понятий: замкнутой ломаной линии или соответствующей части плоскости. В первом случае соответствующую фигуру естественно назвать одномерным многоугольником, а во втором – многоугольником двумерным.
Многоугольники, и в первую очередь выпуклые, можно классифицировать по числу сторон, свойствам, связанным с расположением сторон и их равенством: треугольники, четырехугольники и т.д., параллелограммы и трапеции, правильные и полуправильные.
В частности, многоугольник называют правильным, если равны все его стороны и равны все его внутренние углы. Если первое условие выполняется, а второе нет, то многоугольник называют полуправильным. В школьном курсе геометрии рассматриваются некоторые виды правильных и полуправильных многоугольников: правильные треугольники, четырех и шестиугольники (иногда пятиугольники), полуправильные четырехугольники – ромбы.
Вопрос существования правильных многоугольников связан с вопросом о возможности деления окружности на n равных частей. При решении этой задачи циркулем и линейкой обнаруживается невозможность ее решения в общем виде. Со времен К.Гаусса (1777 – 1855гг.) известно, что этими средствами, например, нельзя разделить окружность на семь равных частей, а значит и построить правильный семиугольник (см. Б.И.Аргунов, М.Б.Балк, Элементарная геометрия, Москва, 1966 г.).
Таким образом, если связать проблему существования фигуры с возможностью ее построения теми или иными средствами, например, циркулем и линейкой, то она оказывается неразрешимой в общем виде.
3º. Многогранники.
Совокупность плоских многоугольников, состоящая более чем из одного многоугольника, называют связной, если любые две вершины этих многоугольников соединены ломаной линией, звеньями которой являются стороны многоугольников этой совокупности.
Связная совокупность многоугольников, не принадлежащих одной плоскости, называется многогранной поверхностью. Многоугольники, образующие эту поверхность, называют гранями поверхности, их стороны – ребрами поверхности, а вершины многоугольников – вершинами многогранной поверхности.
Ребра поверхности, являющиеся сторонами более чем одной грани называют внутренними, а принадлежащие одной грани – краевыми. Многогранная поверхность без краевых ребер называется многогранником.
Многогранники, как и многоугольники, делят на простые и звездчатые. Многогранник называется простым, если каждая его вершина является вершиной только одного многогранного угла и не является внутренней точкой никакого ребра и никакой грани, ребра и грани не имеют общих внутренних точек. Многогранники, не удовлетворяющие перечисленным выше условиям, называют звездчатыми.
Использованное здесь понятие многогранного угла может быть определено как совокупность плоских углов 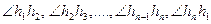 , образованных лучами h 1, h 2, …, h n-1, h n, имеющими общее начало и никакие три из которых не принадлежат одной плоскости, при условии, что n
, образованных лучами h 1, h 2, …, h n-1, h n, имеющими общее начало и никакие три из которых не принадлежат одной плоскости, при условии, что n 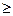 3.
3.
Дальнейшая классификация связана, прежде всего, с выделением из класса простых многогранников класса многогранников выпуклых.
Многогранник называют выпуклым, если он расположен по одну сторону от любой плоскости, содержащей грань многогранника (естественно, за исключением самой этой грани). Грани выпуклого многогранника – выпуклые многоугольники.
Многогранник называют правильным, если все его грани – правильные одноименные и равные между собой многоугольники, а все многогранные углы при его вершинах равны между собой.
Как и в случае многоугольников, для правильных многогранников возникает естественный вопрос о видах этих многогранников. При этом их классификация связывается как с числом граней, так и с типом этих граней как правильных многоугольников. Для ответа на поставленный вопрос, прежде всего обратимся к замечательной теореме, носящей имя знаменитого русского математика Л.Эйлера (1707-1783 гг.).
4º. Теорема Эйлера.
Введем понятие рода многогранника.
Разрезом многогранника называют всякую замкнутую ломаную линию, звеньями которой являются ребра данного многогранника.
Говорят, что разрез многогранники разбивает его на части, если существуют точки, принадлежащие многограннику, для которых любая ломаная линия, их соединяющая и принадлежащая многограннику, пересекает разрез многогранника.
Замечание: Здесь, естественно, грани многогранника – это плоские многоугольники как части плоскостей их содержащих.
Многогранник называют многогранником нулевого рода, если любой его разрез разбивает многогранник на части.
Простой многогранник является многогранником нулевого рода.
Замечание: Максимальное число разрезов, не разбивающих многогранник на части, называют родом многогранника.
Вот пример многогранника 2го рода (рис. 71).
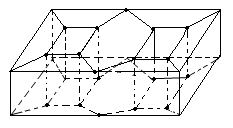
Рис. 71
Образно описывая такой многогранник можно представить его как пластину с двумя дырами, имеющими вид параллелепипедов. Верхние и нижние вершины параллелепипедов при этом должны быть соединены с точками ребер верхней и нижней граней пластины, например, так, как показано на рисунке 71. Это необходимо, чтобы пластина с дырами предстала в виде многогранника. Проделывая в пластине любое число дыр, будем получать примеры многогранников любого конечного рода.
Теорема: Соотношение между числами вершин, граней и ребер многогранника нулевого рода представляется равенством В + Г – Р = 2, где В – число вершин, Г – число граней, Р – число ребер.
Впервые эта закономерность установлена Р.Декартом в 1620 году и заново открыта Л.Эйлером в 1752 году. По этой причине ее правильно назвать зависимостью Декарта-Эйлера.
При доказательстве теоремы будем использовать разрезы многогранника, представляющие замкнутые ломаные линии, образованные ребрами одной грани. Эту процедуру будем называть вырезанием грани. Итак, последовательно вырезаем грани многогранника.
1. Вырезаем (любую) первую грань. Остается многогранная поверхность у которой число граней г1 = Г – 1, число вершин в1 = В и число ребер р1 = Р. В результате получим: В + Г – Р = в1 + (г1 + 1) – р1 =
=(в1 + г1 – р1) + 1.
2. Далее вырезаем грани из многогранной поверхности с краевыми ребрами:
· На первом шаге вырезаемая грань имеет одно краевое ребро, поэтому у оставшейся многогранной поверхности число граней
г2 = г1 – 1, число вершин в2 = в1, число ребер р2 = р1 – 1. Таким образом,
в2 + г2 – р2 = в1 + (г1 – 1) – (р1 – 1) = в1 + г1 – р1
· На k-ом шаге вырезаем грань с k–1 краевым ребром поэтому
гk = гk –1, вk = вk-1 – (k–2), pk = pk-1 – (k–1). Таким образом,
вk + гk – рk = вk-1 – (k – 2) + гk – 1 – рk-1 + (k – 1) = вk-1 + гk-1 – рk-1.
Вывод: соотношение вi + гi – рi не меняется для любого значения i, начиная с i = 1. Иначе говоря, вi + гi – рi = в1 + г1 – р1.
Через конечное число шагов от многогранной поверхности останется простой многоугольник, число сторон и вершин которого одинаково, обозначим его n. Для этого многоугольника, как «многогранной поверхности», число граней г = 1, число вершин в = n, число ребер р = n. Поэтому в + г – р = n + 1 – n = 1. Но из вi + гi – рi = в1 + г1 – р1 и вi + гi – рi = в + г – р = 1 получаем в1 + г1 – р1 = 1.
Возвращаясь к соотношению шага 1, получаем равенство В + Г – Р = 1 + 1 = 2. Теорема доказана полностью.
Доказанная теорема может быть обобщена на многогранник k -го рода: В + Г – Р = 2 – k. (См. например, Б.И.Аргунов, М.Б.Балк, Элементарная геометрия, стр. 104-105).
5º. Правильные многогранники.
Всякий правильный многогранник, будучи многогранником выпуклым, а потому и простым, является многогранником нулевого рода. Поэтому для него справедлива теорема Эйлера в той формулировке, в какой мы ее выше рассматривали. Докажем, что правильных многогранников существует ровно пять видов, при делении их на виды по числу граней и виду самих граней как правильных многоугольников. Прежде всего, докажем, что их может существовать не более пяти видов. Обобщим понятие правильного многогранника и докажем соответствующее утверждение для многогранников этого обобщенного вида.
Назовем многогранник топологически правильным, если он образован одноименными выпуклыми многоугольниками и в каждой вершине многогранника сходится одинаковое число ребер. Последнее условие означает, что все многогранные углы многогранника при его вершинах – одноименные (трехгранные, или четырехгранные, или пятигранные и т.д.).
Теорема: может существовать не более пяти видов топологически правильных многогранников.
Прежде всего заметим, что топологически правильный многогранник является многогранником нулевого рода. Пусть его гранями являются выпуклые одноименные n -угольники и в каждой вершине многогранника сходится s его ребер, то есть его многогранные углы при вершинах – s – гранные. В этом случае, если В, Г и Р – числа вершин, граней и ребер многогранника, то очевидно, что n .Г = 2Р и s .В = 2Р. Отметим, что В + Г – Р = 2 и 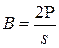 и
и 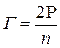 . Отсюда получаем:
. Отсюда получаем: 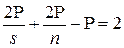 . Делим обе части последнего равенства на 2Р, получаем
. Делим обе части последнего равенства на 2Р, получаем 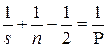 или
или 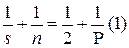 . Кроме того, из геометрических соображений n
. Кроме того, из геометрических соображений n 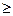 3 и s
3 и s 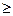 3.
3.
Рассматриваем геометрически возможные случаи сочетаний значений n и s:
1. Пусть одновременно n 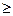 4 и s
4 и s 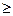 4. Тогда
4. Тогда 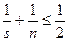 , а потому не выполняется равенство (1). Значит, n и s одновременно не могут удовлетворять неравенствам
, а потому не выполняется равенство (1). Значит, n и s одновременно не могут удовлетворять неравенствам 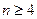 и
и 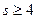 .
.
2. Ни одно из чисел n и s не может быть больше 5. Допустим, что n 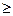 6 и s = 3, тогда
6 и s = 3, тогда 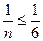 и
и 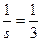 .
.
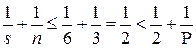 . Равенство (1) не выполняется. Тем более оно не будет выполняться, если s >3.
. Равенство (1) не выполняется. Тем более оно не будет выполняться, если s >3.
То же самое получим при n = 3 или n > 3 и s 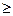 6.
6.
Вывод: 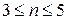 и
и 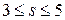 и одновременно не может быть
и одновременно не может быть 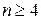 и
и 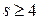 .
.
Теперь можно перебрать все возможные комбинации значений натуральных чисел n и s.
1. n = 3 и s = 3. Тогда 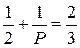 , решением этого уравнения будет
, решением этого уравнения будет
Р= 6. Используя, представленные в доказательстве предыдущей теоремы, выражения В и Г через Р, получим В = 4 и Г = 4. По числу граней такой многогранник естественно назвать четырехгранником, по-гречески тетраэдр. Его гранями являются треугольники.
Аналогичные подсчеты дают нам и остальные возможные случаи топологически правильных многогранников.
2. n = 3 и s = 4. В этом случае Р = 12, В = 6 и Г = 8. Восьмигранник или по-гречески октаэдр.
3. n = 3 и s = 5. Тогда Р = 30, В = 12 и Г = 20, то есть двадцатигранник или икосаэдр.
4. n = 4 и s = 5. Отсюда Р = 12, В = 8 и Г = 6 – шестигранник или гексаэдр, в русской литературе – куб.
5. n = 5 и s = 3. Здесь Р = 30, В = 20 и Г = 12. Такой двенадцатигранник по-гречески называется додекаэдром.
Теперь остается доказать существование этих пяти видов топологически правильных многогранников. Поскольку нас интересует конкретно существование правильных многогранников, то и уделим внимание только этому виду топологически правильных многогранников. Решим этот вопрос конструктивно, то есть путем построения соответствующего вида правильного многогранника. Ограничимся двумя видами этих многогранников: тетраэдром и икосаэдром, предоставляя читателю три остальных случая в качестве самостоятельной работы.
Случай 1 – правильный тетраэдр.
Построение с помощью циркуля и линейки.
1. В плоскости α (произвольно выбранная плоскость) циркулем и линейкой строим правильный треугольник, стороной которого является произвольно выбранный отрезок а (рис. 72). Обозначим его вершины через А, В и С.
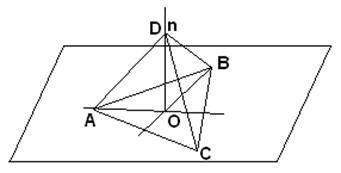
Рис. 72
2. Строим центр 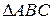 и обозначаем его буквой О.
и обозначаем его буквой О.
3. Строим прямую n, проходящую через О перпендикулярно к α.
4. От точки О на n откладываем отрезок OD, равный 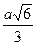
5. Соединяем точки А и D, В и D, С и D.
Получаем тетраэдр DABC, у которого все ребра равны а и все трехгранные углы при вершинах D, A, В и С равны как трехгранные углы с равными плоскими углами.
Таким образом, построенный тетраэдр – правильный.
Замечание. Выполнить построение тетраэдра в полном объеме только циркулем и линейкой, конечно, невозможно, так как необходим выход из плоскости в пространство (построение перпендикуляра n к α). Поэтому мы использовали построение перпендикуляра к плоскости как известную задачу.
Случай 2 – правильный икосаэдр.
Построение с помощью циркуля и линейки.
1. Построение икосаэдра не обязательно правильного (подготовительный этап) – рисунок 73.
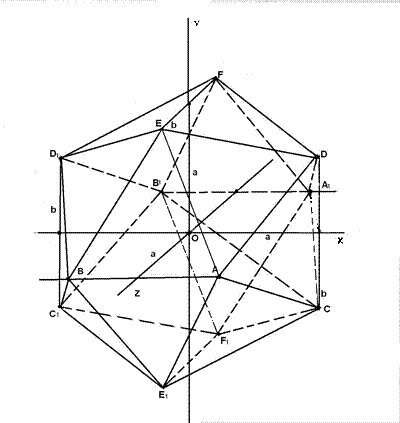
Рис. 73
· Строим три пересекающиеся в одной точке и взаимно перпендикулярные прямые x, y и z. Пусть О – точка их пересечения.
· От точки О на каждой из этих прямых в обе стороны откладываем отрезки, равные произвольно выбранному отрезку а.
· Через точки оси z проводим прямые, параллельные оси х, через точки оси у – параллельные оси z, через точки оси x – прямые, параллельные оси y.
· На этих прямых в обе стороны от точек, лежащих на первых шести прямых, откладываем отрезки, равные произвольно выбранному отрезку b. Получаем 12 точек А, В, А 1, В 1, С, D, С 1, D 1, Е, F, Е 1, F 1.
· Точку А соединяем с четырьмя точками Е, D, С, Е 1, точку В с точками Е, D 1, С 1, Е 1 и т.д. В результате получаем многогранник с 20 гранями, 12 вершинами и 30 ребрами, иначе говоря – икосаэдр.
2. Построение правильного икосаэдра.
Найдем соотношение между отрезками а и b, при котором грани построенного выше икосаэдра окажутся правильными треугольниками. Используем рисунок 74, на котором выделена одна грань АВЕ построенного нами икосаэдра.
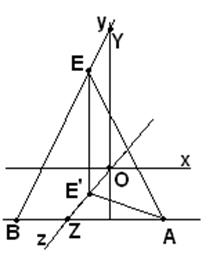
Рис. 74
Точку пересечения EF с у обозначим буквой Y, а точку пересечения АВ с осью z – буквой Z. Отметим, что OZ = а и AZ = BZ = EY = b, треугольник АВЕ – равнобедренный (АЕ = ВЕ по построению). Найдем условие, связывающее отрезки а и b, при котором 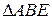 окажется правильным (то есть АЕ = АВ).
окажется правильным (то есть АЕ = АВ).
Проектируем Е на плоскость осей x и z. Получаем точку 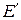 .
. 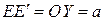 .
. 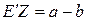 (b выбираем с условием
(b выбираем с условием 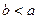 ). Тогда из
). Тогда из 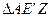 :
:
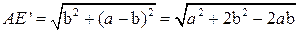 .
.
Из 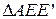 :
: 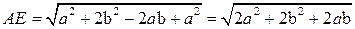 . Так как мы хотим, чтобы АЕ = АВ, то
. Так как мы хотим, чтобы АЕ = АВ, то 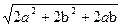 = 2 b. Отсюда
= 2 b. Отсюда 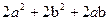 = 4 b 2 или
= 4 b 2 или 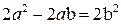 . Получаем уравнение
. Получаем уравнение 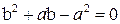 .
.
Вывод: Если при произвольно выбранном отрезке а за отрезок b принять 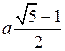 , то треугольник АВЕ окажется правильным, то есть все грани выше построенного икосаэдра окажутся правильными треугольниками, стороны каждого из которых равны а (
, то треугольник АВЕ окажется правильным, то есть все грани выше построенного икосаэдра окажутся правильными треугольниками, стороны каждого из которых равны а (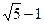 ).
).
Для доказательства равенства всех многогранных углов при вершинах икосаэдра используем: симметрию относительно плоскостей хОу, xOz и yOz, центральную симметрию с центром О и осевые повороты, оси которых проходят через центр симметрии – точку О.
Детальное рассмотрение этих процедур рекомендуем читателю для самостоятельной работы, целесообразно также самостоятельно выполнить доказательство существования и оставшихся трех возможных случаев правильных многогранников (октаэдра, гексаэдра и додекаэдра).
Лекция 5.







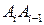 и A i A i+1. Эти лучи образуют угол, который можно обозначить как
и A i A i+1. Эти лучи образуют угол, который можно обозначить как 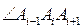 . Этот угол называют внутренним углом многоугольника
. Этот угол называют внутренним углом многоугольника
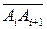 ,противоположным лучу A i A i+1, называют внешним углом многоугольника (рис. 49, его правая часть).
,противоположным лучу A i A i+1, называют внешним углом многоугольника (рис. 49, его правая часть).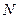 – точка внешней области.
– точка внешней области.
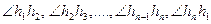 , образованных лучами h 1, h 2, …, h n-1, h n, имеющими общее начало и никакие три из которых не принадлежат одной плоскости, при условии, что n
, образованных лучами h 1, h 2, …, h n-1, h n, имеющими общее начало и никакие три из которых не принадлежат одной плоскости, при условии, что n 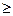 3.
3.
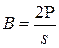 и
и 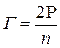 . Отсюда получаем:
. Отсюда получаем: 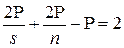 . Делим обе части последнего равенства на 2Р, получаем
. Делим обе части последнего равенства на 2Р, получаем 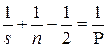 или
или 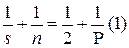 . Кроме того, из геометрических соображений n
. Кроме того, из геометрических соображений n 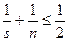 , а потому не выполняется равенство (1). Значит, n и s одновременно не могут удовлетворять неравенствам
, а потому не выполняется равенство (1). Значит, n и s одновременно не могут удовлетворять неравенствам 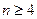 и
и 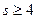 .
.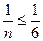 и
и 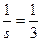 .
.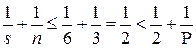 . Равенство (1) не выполняется. Тем более оно не будет выполняться, если s >3.
. Равенство (1) не выполняется. Тем более оно не будет выполняться, если s >3.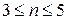 и
и 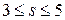 и одновременно не может быть
и одновременно не может быть 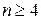 и
и 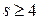 .
.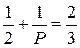 , решением этого уравнения будет
, решением этого уравнения будет
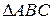 и обозначаем его буквой О.
и обозначаем его буквой О.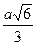


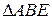 окажется правильным (то есть АЕ = АВ).
окажется правильным (то есть АЕ = АВ).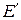 .
. 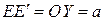 .
. 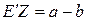 (b выбираем с условием
(b выбираем с условием 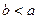 ). Тогда из
). Тогда из 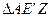 :
: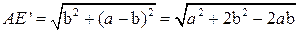 .
.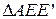 :
: 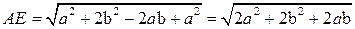 . Так как мы хотим, чтобы АЕ = АВ, то
. Так как мы хотим, чтобы АЕ = АВ, то 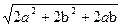 = 2 b. Отсюда
= 2 b. Отсюда 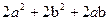 = 4 b 2 или
= 4 b 2 или 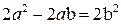 . Получаем уравнение
. Получаем уравнение 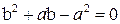 .
.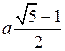 , то треугольник АВЕ окажется правильным, то есть все грани выше построенного икосаэдра окажутся правильными треугольниками, стороны каждого из которых равны а (
, то треугольник АВЕ окажется правильным, то есть все грани выше построенного икосаэдра окажутся правильными треугольниками, стороны каждого из которых равны а (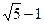 ).
).


