Прежде всего о математическом смысле слов «коллинеарность» и «конкурентность». Для множества точек, содержащего более двух точек говорят, что точки коллинеарны, если они принадлежат одной прямой, или существует прямая, их содержащая. Термин конкурентность употребляется для ситуации, когда несколько прямых (более двух) пересекается в одной точке (или проходят через одну точку).
1  . Рассмотрим некоторые признаки коллинеарности трех точек и конкурентности трех прямых. Один из признаков коллинеарности рассмотрен нами во второй лекции. Здесь мы затронем теоремы, доказательства которых растянулись на много столетий от 100 года нашей эры до 19 столетия нашей эры.
. Рассмотрим некоторые признаки коллинеарности трех точек и конкурентности трех прямых. Один из признаков коллинеарности рассмотрен нами во второй лекции. Здесь мы затронем теоремы, доказательства которых растянулись на много столетий от 100 года нашей эры до 19 столетия нашей эры.
Менелаю Александрийскому (I-II в. в. н. э.) приписывается теорема, которая естественно может рассматриваться как одно из условий принадлежности трех точек одной прямой. Именно как такое условие мы её и формулируем
Теорема Менелая: Три точки M, N и P, две из которых (например M и N) принадлежат двум сторонам 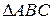 , а третья (точка Р) – продолжению его третьей стороны, коллинеарны тогда и только тогда, когда произведение трех отношений, в которых эти точки делят соответствующие стороны треугольника равно 1.
, а третья (точка Р) – продолжению его третьей стороны, коллинеарны тогда и только тогда, когда произведение трех отношений, в которых эти точки делят соответствующие стороны треугольника равно 1.
Если  и Р принадлежит продолжению стороны АС, то условие представляется равенством
и Р принадлежит продолжению стороны АС, то условие представляется равенством  . Удобнее всего записывать это равенство, «двигаясь» от одной из вершин треугольника (в принципе любой) к другой, обходя треугольник по «часовой» или «против часовой» стрелке (рис. 58).
. Удобнее всего записывать это равенство, «двигаясь» от одной из вершин треугольника (в принципе любой) к другой, обходя треугольник по «часовой» или «против часовой» стрелке (рис. 58).

Рис. 58
Докажем эту теорему, используя признаки подобия треугольников.
1. Пусть M, N и P принадлежат одной прямой. Опустим перпендикуляры из A, B и C на прямую MN. Выделяем три пары прямоугольных треугольников: 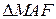 и
и  ,
, 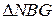 и
и  ,
,  и
и 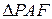 . В каждой из этих пар треугольники подобны (в силу конгруэнтности соответствующих пар углов). На основании этого пары соответствующих сторон каждой пары подобных треугольников пропорциональны. Выделяем пропорции:
. В каждой из этих пар треугольники подобны (в силу конгруэнтности соответствующих пар углов). На основании этого пары соответствующих сторон каждой пары подобных треугольников пропорциональны. Выделяем пропорции:  ,
, 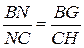 и
и  . Перемножаем левые и правые части полученных равенств
. Перемножаем левые и правые части полученных равенств  . Таким образом
. Таким образом  .
.
2. Пусть теперь точки M, N и P таковы, что  .
.
Доказательство того, что точки M, N и P лежат на одной прямой проведем методом «от противного».
Допустим, что прямая МР не содержит точку N. В силу аксиомы Паша (акс. II4) МР пересекает ВС. Точку пересечения обозначим N1. В силу доказанного выше  . Используя условие получаем
. Используя условие получаем  . Отсюда
. Отсюда  . На отрезке ВС оказались две точки, делящие его в одном отношении, что невозможно.
. На отрезке ВС оказались две точки, делящие его в одном отношении, что невозможно.
Полученное противоречие – следствие допущения. Для устранения противоречия приходится отбросить допущение, т. е. приходится признать, что точка N принадлежит прямой МР. Иначе говоря, точки M, N и P коллинеарны.
Замечание: Теорема верна и для точек, лежащих на продолжениях сторон треугольника.
Другое условие коллинеарности трех точек выражено в теореме, доказательство которой принадлежит Паппу Александрийскому, жившему в конце III в. н. э.
Теорема Паппа: Если две тройки  и
и  попарно противоположных вершин шестиугольника
попарно противоположных вершин шестиугольника 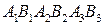 лежат на двух прямых a и b соответственно, то точки пересечения M, N и L пар его противоположных сторон (прямых на которых они лежат) A 1 B 1 и B 2 A 3, B 1 A 2 и А 3 В 3, А 2 В 2 и В 3 А 1 лежат на одной прямой.
лежат на двух прямых a и b соответственно, то точки пересечения M, N и L пар его противоположных сторон (прямых на которых они лежат) A 1 B 1 и B 2 A 3, B 1 A 2 и А 3 В 3, А 2 В 2 и В 3 А 1 лежат на одной прямой.
Напоминаем, что вершины или стороны шестиугольника считаются противоположными, если при обходе шестиугольника вдоль его сторон они окажутся удаленными друг от друга на две вершины или, соответственно, две стороны. Таким образом, для многоугольника 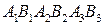 (его вершины упорядочены в записи) для A 1 противоположна вершина B 2 , для A 2 – вершина В 3, а для А 3 – вершина B 1. Пусть при этом a – прямая, содержащая A 1, A 2, A 3, а прямая b содержит вершины B 1, B 2, В 3 (рис. 59).
(его вершины упорядочены в записи) для A 1 противоположна вершина B 2 , для A 2 – вершина В 3, а для А 3 – вершина B 1. Пусть при этом a – прямая, содержащая A 1, A 2, A 3, а прямая b содержит вершины B 1, B 2, В 3 (рис. 59).
 Рис. 59
Рис. 59
Обратим внимание на то, что формулировка теоремы предполагает, что каждые две прямые, содержащие пары противоположных сторон, пересекаются. Именно для этого случая мы и докажем эту теорему. Однако нетрудно понять, что на евклидовой плоскости хотя бы одна из таких пар может лежать и на параллельных прямых. Будут ли в таких случаях точки M, N и L лежать на одной прямой? Сейчас мы оставим этот вопрос в стороне, доказав один из них во второй части нашего курса.
Отметим точки пересечения пар прямых A 1 B 1 и B 2 A 3, B 1 A 2 и А 3 В 3, А 2 В 2 и В 3 А 1 , обозначив их буквами M, N и L. Требуется доказать, что точки M, N и L принадлежат одной прямой. Пусть прямые А 1 В 3 и B 2 A 3 пересекаются в точке R, прямые А 1 В 3 и A 2 B 1 – в точке T и прямые А 2 В 2 и А 1 В 3 – в точке S.
Применяем теорему Менелая к пяти тройкам точек { L, А 2, В 2 }, { В 3, N, A 3 }, { A 1, M, В 1}, { B 1, В 2, В 3}, { A 1, A 2, А 3}. Каждая из этих троек есть точки, лежащие на сторонах и продолжениях сторон треугольника  , причем по условию каждая тройка – точки одной прямой: первая – прямой А 2 В 2, вторая – прямой А 3 В 3, третья – прямой A 1 B 1, четвертая – прямой b, пятая – прямой a.
, причем по условию каждая тройка – точки одной прямой: первая – прямой А 2 В 2, вторая – прямой А 3 В 3, третья – прямой A 1 B 1, четвертая – прямой b, пятая – прямой a.
Таким образом можно записать пять равенств:
 ,
,  ,
,  ,
,  ,
,  .
.
Перемножив первые три и последние два равенства, получаем:
 (1)
(1)
 (2)
(2)
Делим равенство (1) на равенство (2) и получаем 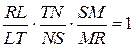 . Последнее означает, что точки M, N и L принадлежат одной прямой.
. Последнее означает, что точки M, N и L принадлежат одной прямой.
2  Следующая теорема трактует о связи между конкурентностью прямых и коллинеарностью точек. Ее доказательство принадлежит архитектору Жерару Дезаргу, жившему в 1591-1661 годах.
Следующая теорема трактует о связи между конкурентностью прямых и коллинеарностью точек. Ее доказательство принадлежит архитектору Жерару Дезаргу, жившему в 1591-1661 годах.
Теорема: Если два треугольника АВС и EFG перспективны, то пары их соответствующих сторон СА и EG, BA и FE и BC и FG пересекаются в коллинеарных точках L, M и N соответственно.
На рис. 60 представлена эта конфигурация.

Рис. 60
Конечно, речь идет лишь о том случае, когда пары указанных прямых пересекаются. Это условие, вообще говоря, не обязательно. В части II нашего курса этот случай будет рассматриваться отдельно. Напомним также, что перспективность треугольников означает не только случай, представленный на рисунке, но и тот, когда соответствующие прямые параллельны (AE || BF || CG).
Перейдем к доказательству теоремы. Применим теорему Менелая к тройкам точек { L, E, G }, { M, E, F }, и { N, G, F }, принадлежащим продолжениям сторон треугольников  ,
,  и
и  .
.
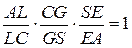 ,
, 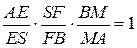 ,
, 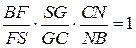 . Перемножаем эти равенства и после сокращений получаем
. Перемножаем эти равенства и после сокращений получаем  . Точки L, M и N лежат на продолжениях сторон СА, АВ и BC треугольника
. Точки L, M и N лежат на продолжениях сторон СА, АВ и BC треугольника  . По теореме Менелая полученное равенство означает принадлежность точек L, M и N одной прямой.
. По теореме Менелая полученное равенство означает принадлежность точек L, M и N одной прямой.
Отметим теперь теорему, которая может истолковываться как условие конкурентности трех прямых. Ей является так называемая теорема Чевы (Д. Чева, 1678 год).
Теорема Чевы: Три прямые, проходящие через вершины треугольника 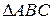 , конкурентны тогда и только тогда, когда точки их пересечения со сторонами треугольника (или их продолжениями) M, N и P делят соответствующие им стороны в отношениях, произведение которых равно 1.
, конкурентны тогда и только тогда, когда точки их пересечения со сторонами треугольника (или их продолжениями) M, N и P делят соответствующие им стороны в отношениях, произведение которых равно 1.
Если  ,
,  и
и  , то это условие выглядит как
, то это условие выглядит как  (рис. 61).
(рис. 61).

Рис. 61
Эту теорему можно доказать, используя теорему Менелая.
1. Пусть AM, BN и CP пересекаются в одной точке S. Докажем, что тогда  .
.  и прямая CP и
и прямая CP и  и прямая BN находятся в условиях теоремы Менелая, а потому имеем два равенства:
и прямая BN находятся в условиях теоремы Менелая, а потому имеем два равенства:  и
и  . Перемножая эти равенства почленно, получаем
. Перемножая эти равенства почленно, получаем  .Произведя сокращения, приходим к равенству
.Произведя сокращения, приходим к равенству  или
или  .
.
2. Обратное, пусть  . Докажем, что прямые AM, BN и CP пересекаются в одной точке. Сделать это можно, используя метод «от противного».
. Докажем, что прямые AM, BN и CP пересекаются в одной точке. Сделать это можно, используя метод «от противного».
Итак, допустим, что AM, BN и CP не проходят через одну точку, иначе говоря AM пересекается BN и CP в разных точках. Обозначим точку пересечения AM и CP через S 1 и проведем прямую BS 1. Пусть она пересекает AC в точке N 1. Ясно, что N 1 и N – различные точки. Для прямых AM, B N 1 и CP выполнено условие того, что  (пункт 1).
(пункт 1).
Возвращаясь к тому, что дано, получаем равенство  , из которого следует
, из которого следует  .
.
Таким образом, две различные точки N и N 1 прямой AC делят отрезок AC в одном и том же отношении. Это противоречит известному факту о делении отрезка в заданном отношении: делящая точка единственна. Противоречие оказалось следствием допущения. Поэтому его приходится отбросить. Итак, AM, BN и CP проходят через одну точку.
3  Отметим в заключении ещё два утверждения о коллинеарности точек и прямых, которые, как правило, не рассматриваются в евклидовой геометрии, но по методу доказательства к ней могут быть отнесены. Первое из них – теорема Паскаля, которую Паскаль доказал в 16-ти летнем возрасте. Подлинный текст доказательства был утерян. С проективной точки зрения эта теорема может рассматриваться как обобщение теоремы Паппа. В этой теореме речь идет о вписанном в линию второго порядка шестиугольнике. Мы ограничимся окружностью.
Отметим в заключении ещё два утверждения о коллинеарности точек и прямых, которые, как правило, не рассматриваются в евклидовой геометрии, но по методу доказательства к ней могут быть отнесены. Первое из них – теорема Паскаля, которую Паскаль доказал в 16-ти летнем возрасте. Подлинный текст доказательства был утерян. С проективной точки зрения эта теорема может рассматриваться как обобщение теоремы Паппа. В этой теореме речь идет о вписанном в линию второго порядка шестиугольнике. Мы ограничимся окружностью.
Теорема Паскаля: Если ABCDEF – шестиугольник, вписанный в окружность, то точки пересечения пар прямых, каждая из которых содержит одну из сторон соответствующей пары противоположных сторон шестиугольника, коллинеарны.
Обратим внимание на то, что это утверждение верно для любого из 60-ти возможных многоугольников, вершинами которых являются точки A,B,C,D,E и F. Стороны считаются противоположными, если их разделяют ровно две стороны шестиугольника при последовательном обходе его вершин. Теорема Паскаля верна для любого из них, если, конечно, пересечение прямых толковать в расширенном смысле, допуская и понятие бесконечно удаленной точки. Мы рассматриваем случаи, которые характерны для евклидовой плоскости (рис. 62).
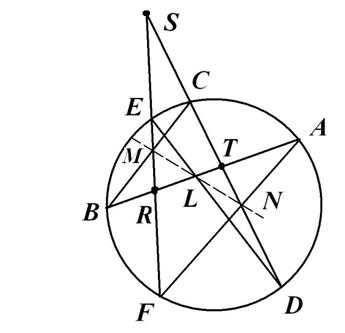
Рис. 62
Пары противоположных сторон ABCDEF – это AB и ED, BC и EF, CD и FA, точки их пересечения L, M и N соответственно. Требуется доказать, что L, M и N принадлежат одной прямой.
Пусть прямые AB, CD и EF попарно пересекаются в точках T, S, R. Рассматриваем  и прямые DE, BC и FA, пересекающие его «стороны» в точках L, M и N. Тройки коллинеарных точек { D, L, E }, { В, M, C }, и { A, N, F } лежат каждая на трех «сторонах»
и прямые DE, BC и FA, пересекающие его «стороны» в точках L, M и N. Тройки коллинеарных точек { D, L, E }, { В, M, C }, и { A, N, F } лежат каждая на трех «сторонах»  а потому по теореме Менелая имеем три равенства
а потому по теореме Менелая имеем три равенства  ,
,  и
и  . Перемножив эти равенства, получим:
. Перемножив эти равенства, получим:  (1)
(1)
По теоремам о хордах и секущих одной окружности
 и
и  (2)
(2)
Из произведения отношений 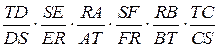 соответствующей перестановкой сомножителей и группировкой частных получаем
соответствующей перестановкой сомножителей и группировкой частных получаем
 , (3)
, (3)
т. к. числители и знаменатели всех трех дробей равны (в силу равенств 2). В силу равенства (1) и равенства (3) приходим к равенству  или
или  . По теореме Менелая для
. По теореме Менелая для  и точек L, M и N заключаем: L, M и N принадлежат одной прямой. Для рассматривавшегося случая теорема Паскаля доказана. Доказательства для остальных 59-ти случаев аналогичны.
и точек L, M и N заключаем: L, M и N принадлежат одной прямой. Для рассматривавшегося случая теорема Паскаля доказана. Доказательства для остальных 59-ти случаев аналогичны.
Переходим к последней широко известной теореме о конкурентности прямых, связанных с шестиугольником. Эта теорема принадлежит Ш. Брианшону (1785-1864) и носит его имя. Мы докажем её методами евклидовой геометрии, не используя принципа двойственности, характерного для проективной плоскости, рассматривая лишь частный случай кривой второго порядка – окружность. Доказательство принадлежит А. С. Смогоржевскому (Линейка в геометрических построениях, М., Гостехиздат, 1957 г.) и опирается на простой факт (см. рис. 63): если к окружности (O,R) в точках P и Q проведены касательные и на них по одну и ту же сторону от прямой PQ отложены равные отрезки  и
и 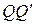 соответственно, то существует окружность, касающаяся прямых
соответственно, то существует окружность, касающаяся прямых  и
и 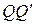 в точках
в точках  и
и  .
.

Рис. 63
Теорема Брианшона: Если шестиугольник описан около окружности, то три его диагонали, каждая из которых соединяет противоположные вершины, конкурентны (рис. 64).

Рис. 64
ABCDEF - шестиугольник, описанный около окружности (O,R). P, Q, R, S, T, U – точки касания окружности (O,R) сторон шестиугольника ABCDEF.
 (1)
(1)
Соответственно  точки, принадлежащие PF, QB, RB, SD, TD и UF. О 1, О 2, и О 3 – центры окружностей, касающихся
точки, принадлежащие PF, QB, RB, SD, TD и UF. О 1, О 2, и О 3 – центры окружностей, касающихся  в точках
в точках 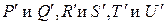 соответственно.
соответственно.
Так как соответствующие отрезки касательных, проведенных к окружности из одной точки, равны, то  и
и  (с учетом конгруэнтностей (1)). Отсюда
(с учетом конгруэнтностей (1)). Отсюда  . Точно так же
. Точно так же  . Поэтому точка A имеет равные степени относительно (O2,R2) и (O3,R3) и точно так же D имеет равные степени относительно этих же окружностей. Значит AD – радикальная ось (O2,R2) и (O3,R3).
. Поэтому точка A имеет равные степени относительно (O2,R2) и (O3,R3) и точно так же D имеет равные степени относительно этих же окружностей. Значит AD – радикальная ось (O2,R2) и (O3,R3).
Аналогично прямая  – радикальная ось окружностей (O1,R1) и (O2,R2), прямая CF – радикальная ось (O1,R1) и (O3,R3). Но радикальные оси трех окружностей, центры которых не принадлежат одной прямой, пересекаются в одной точке (см. лекцию 1). Таким образом, диагонали AD, BE и CF конкурентны.
– радикальная ось окружностей (O1,R1) и (O2,R2), прямая CF – радикальная ось (O1,R1) и (O3,R3). Но радикальные оси трех окружностей, центры которых не принадлежат одной прямой, пересекаются в одной точке (см. лекцию 1). Таким образом, диагонали AD, BE и CF конкурентны.
Замечания.
1. Следует обратить внимание на логическую последовательность теорем Менелая, Паппа, Дезарга и Чевы. Все они в приведенных вариантах доказательств – следствия теоремы Менелая. Доказательство последней базируется на признаках подобия треугольников, а значит на теории пропорций. Иначе говоря, эти теоремы представлены как следствия теории пропорций.
2. Эти теоремы, будучи интересными сами по себе, и с точки зрения их использования в решении задач, связанных с коллинеарностью точек и конкурентностью прямых, имеют ещё и значение в решении вопроса о связи арифметики и геометрии.
Лекция 4



 . Рассмотрим некоторые признаки коллинеарности трех точек и конкурентности трех прямых. Один из признаков коллинеарности рассмотрен нами во второй лекции. Здесь мы затронем теоремы, доказательства которых растянулись на много столетий от 100 года нашей эры до 19 столетия нашей эры.
. Рассмотрим некоторые признаки коллинеарности трех точек и конкурентности трех прямых. Один из признаков коллинеарности рассмотрен нами во второй лекции. Здесь мы затронем теоремы, доказательства которых растянулись на много столетий от 100 года нашей эры до 19 столетия нашей эры.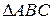 , а третья (точка Р) – продолжению его третьей стороны, коллинеарны тогда и только тогда, когда произведение трех отношений, в которых эти точки делят соответствующие стороны треугольника равно 1.
, а третья (точка Р) – продолжению его третьей стороны, коллинеарны тогда и только тогда, когда произведение трех отношений, в которых эти точки делят соответствующие стороны треугольника равно 1. и Р принадлежит продолжению стороны АС, то условие представляется равенством
и Р принадлежит продолжению стороны АС, то условие представляется равенством  . Удобнее всего записывать это равенство, «двигаясь» от одной из вершин треугольника (в принципе любой) к другой, обходя треугольник по «часовой» или «против часовой» стрелке (рис. 58).
. Удобнее всего записывать это равенство, «двигаясь» от одной из вершин треугольника (в принципе любой) к другой, обходя треугольник по «часовой» или «против часовой» стрелке (рис. 58).
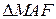 и
и  ,
, 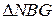 и
и  ,
,  и
и 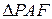 . В каждой из этих пар треугольники подобны (в силу конгруэнтности соответствующих пар углов). На основании этого пары соответствующих сторон каждой пары подобных треугольников пропорциональны. Выделяем пропорции:
. В каждой из этих пар треугольники подобны (в силу конгруэнтности соответствующих пар углов). На основании этого пары соответствующих сторон каждой пары подобных треугольников пропорциональны. Выделяем пропорции:  ,
, 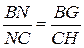 и
и  . Перемножаем левые и правые части полученных равенств
. Перемножаем левые и правые части полученных равенств  . Таким образом
. Таким образом  . Используя условие получаем
. Используя условие получаем  . Отсюда
. Отсюда  . На отрезке ВС оказались две точки, делящие его в одном отношении, что невозможно.
. На отрезке ВС оказались две точки, делящие его в одном отношении, что невозможно. и
и  попарно противоположных вершин шестиугольника
попарно противоположных вершин шестиугольника 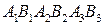 лежат на двух прямых a и b соответственно, то точки пересечения M, N и L пар его противоположных сторон (прямых на которых они лежат) A 1 B 1 и B 2 A 3, B 1 A 2 и А 3 В 3, А 2 В 2 и В 3 А 1 лежат на одной прямой.
лежат на двух прямых a и b соответственно, то точки пересечения M, N и L пар его противоположных сторон (прямых на которых они лежат) A 1 B 1 и B 2 A 3, B 1 A 2 и А 3 В 3, А 2 В 2 и В 3 А 1 лежат на одной прямой. Рис. 59
Рис. 59 , причем по условию каждая тройка – точки одной прямой: первая – прямой А 2 В 2, вторая – прямой А 3 В 3, третья – прямой A 1 B 1, четвертая – прямой b, пятая – прямой a.
, причем по условию каждая тройка – точки одной прямой: первая – прямой А 2 В 2, вторая – прямой А 3 В 3, третья – прямой A 1 B 1, четвертая – прямой b, пятая – прямой a. ,
,  ,
,  ,
,  ,
,  .
. (1)
(1) (2)
(2)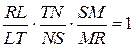 . Последнее означает, что точки M, N и L принадлежат одной прямой.
. Последнее означает, что точки M, N и L принадлежат одной прямой.
 ,
,  и
и  .
.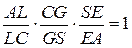 ,
, 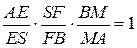 ,
, 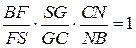 . Перемножаем эти равенства и после сокращений получаем
. Перемножаем эти равенства и после сокращений получаем  . Точки L, M и N лежат на продолжениях сторон СА, АВ и BC треугольника
. Точки L, M и N лежат на продолжениях сторон СА, АВ и BC треугольника  . По теореме Менелая полученное равенство означает принадлежность точек L, M и N одной прямой.
. По теореме Менелая полученное равенство означает принадлежность точек L, M и N одной прямой. ,
,  и
и  , то это условие выглядит как
, то это условие выглядит как  (рис. 61).
(рис. 61).
 и прямая CP и
и прямая CP и  и прямая BN находятся в условиях теоремы Менелая, а потому имеем два равенства:
и прямая BN находятся в условиях теоремы Менелая, а потому имеем два равенства:  и
и  . Перемножая эти равенства почленно, получаем
. Перемножая эти равенства почленно, получаем  .Произведя сокращения, приходим к равенству
.Произведя сокращения, приходим к равенству  или
или  . Докажем, что прямые AM, BN и CP пересекаются в одной точке. Сделать это можно, используя метод «от противного».
. Докажем, что прямые AM, BN и CP пересекаются в одной точке. Сделать это можно, используя метод «от противного». (пункт 1).
(пункт 1). , из которого следует
, из которого следует  .
. Отметим в заключении ещё два утверждения о коллинеарности точек и прямых, которые, как правило, не рассматриваются в евклидовой геометрии, но по методу доказательства к ней могут быть отнесены. Первое из них – теорема Паскаля, которую Паскаль доказал в 16-ти летнем возрасте. Подлинный текст доказательства был утерян. С проективной точки зрения эта теорема может рассматриваться как обобщение теоремы Паппа. В этой теореме речь идет о вписанном в линию второго порядка шестиугольнике. Мы ограничимся окружностью.
Отметим в заключении ещё два утверждения о коллинеарности точек и прямых, которые, как правило, не рассматриваются в евклидовой геометрии, но по методу доказательства к ней могут быть отнесены. Первое из них – теорема Паскаля, которую Паскаль доказал в 16-ти летнем возрасте. Подлинный текст доказательства был утерян. С проективной точки зрения эта теорема может рассматриваться как обобщение теоремы Паппа. В этой теореме речь идет о вписанном в линию второго порядка шестиугольнике. Мы ограничимся окружностью.
 и прямые DE, BC и FA, пересекающие его «стороны» в точках L, M и N. Тройки коллинеарных точек { D, L, E }, { В, M, C }, и { A, N, F } лежат каждая на трех «сторонах»
и прямые DE, BC и FA, пересекающие его «стороны» в точках L, M и N. Тройки коллинеарных точек { D, L, E }, { В, M, C }, и { A, N, F } лежат каждая на трех «сторонах»  ,
,  и
и  . Перемножив эти равенства, получим:
. Перемножив эти равенства, получим:  (1)
(1) и
и  (2)
(2)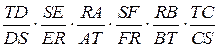 соответствующей перестановкой сомножителей и группировкой частных получаем
соответствующей перестановкой сомножителей и группировкой частных получаем , (3)
, (3) или
или  . По теореме Менелая для
. По теореме Менелая для  и
и 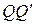 соответственно, то существует окружность, касающаяся прямых
соответственно, то существует окружность, касающаяся прямых  и
и  .
.

 (1)
(1) точки, принадлежащие PF, QB, RB, SD, TD и UF. О 1, О 2, и О 3 – центры окружностей, касающихся
точки, принадлежащие PF, QB, RB, SD, TD и UF. О 1, О 2, и О 3 – центры окружностей, касающихся  в точках
в точках 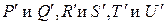 соответственно.
соответственно. и
и  (с учетом конгруэнтностей (1)). Отсюда
(с учетом конгруэнтностей (1)). Отсюда  . Точно так же
. Точно так же  . Поэтому точка A имеет равные степени относительно (O2,R2) и (O3,R3) и точно так же D имеет равные степени относительно этих же окружностей. Значит AD – радикальная ось (O2,R2) и (O3,R3).
. Поэтому точка A имеет равные степени относительно (O2,R2) и (O3,R3) и точно так же D имеет равные степени относительно этих же окружностей. Значит AD – радикальная ось (O2,R2) и (O3,R3). – радикальная ось окружностей (O1,R1) и (O2,R2), прямая CF – радикальная ось (O1,R1) и (O3,R3). Но радикальные оси трех окружностей, центры которых не принадлежат одной прямой, пересекаются в одной точке (см. лекцию 1). Таким образом, диагонали AD, BE и CF конкурентны.
– радикальная ось окружностей (O1,R1) и (O2,R2), прямая CF – радикальная ось (O1,R1) и (O3,R3). Но радикальные оси трех окружностей, центры которых не принадлежат одной прямой, пересекаются в одной точке (см. лекцию 1). Таким образом, диагонали AD, BE и CF конкурентны.

