Будем говорить, что переменная z есть функция аргументов x и y, если каждой паре значений x и y соответствует определенное значение z.
Тот факт, что z есть функция переменных x и y, записывают одной из формул:
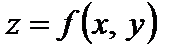 ,
,  ,
,  .
.
Аналогично определяются и обозначаются функции трех и большего числа переменных:
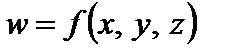 ,
,  и т.д.
и т.д.
Приведем несколько примеров.
Пример 1. Площадь S прямоугольника со сторонами, длины которых равны x и y, выражается формулой
 .
.
Здесь  есть функция двух переменных.
есть функция двух переменных.
Пример 2. Температура Q нагретого тела может в данный момент t изменяться от точки к точке. Поэтому
 ,
,
т.е. Q есть функция трех аргументов (координат точки) x, y и z.
Пример 3. Если в предыдущем примере еще учитывать зависимость Q от времени t, то Q будет функцией четырех аргументов
 .
.
Чтобы задать функцию  , надо не только указать правило нахождения z по заданным x и y, но и то множество пар значений, которые могут принимать аргументы x и y. Это множество называется областью определения функции. В случае явного аналитического задания это множество определяется самой формулой, задающей функцию. Например, функция
, надо не только указать правило нахождения z по заданным x и y, но и то множество пар значений, которые могут принимать аргументы x и y. Это множество называется областью определения функции. В случае явного аналитического задания это множество определяется самой формулой, задающей функцию. Например, функция

задана для всех возможных x и y. Пару чисел  можно рассматривать как координаты точки на плоскости. В связи с этим мы можем сказать, что рассматриваемая функция задана на всей плоскости.
можно рассматривать как координаты точки на плоскости. В связи с этим мы можем сказать, что рассматриваемая функция задана на всей плоскости.
Функция

задана лишь при  , т.е. в круге радиуса R с центром в начале координат, ограниченном окружностью
, т.е. в круге радиуса R с центром в начале координат, ограниченном окружностью  (включая эту окружность).
(включая эту окружность).
Функция

задана при  , т.е. в кольце, ограниченном окружностями радиусов
, т.е. в кольце, ограниченном окружностями радиусов  ,
,  , центр которого совпадает с началом координат (при этом точки, принадлежащие окружности
, центр которого совпадает с началом координат (при этом точки, принадлежащие окружности  принадлежат области определения, а точки окружности
принадлежат области определения, а точки окружности 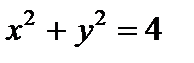 – не принадлежат).
– не принадлежат).
Сформулируем понятие окрестности точки на плоскости.
Определение. Будем называть e - окрестностью точки 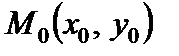 открытый круг радиуса e с центром в точке
открытый круг радиуса e с центром в точке  , т.е. множество точек
, т.е. множество точек 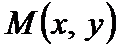 , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям
 .
.
Прямоугольной окрестностью точки 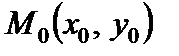 называется открытый прямоугольник с центром точке
называется открытый прямоугольник с центром точке  (т.е. множество точек
(т.е. множество точек 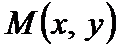 , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям  ,
,  ).
).
В дальнейшем, говоря «окрестность», мы будем иметь в виду окрестность одного из упомянутых видов – круговую или прямоугольную.
Функция двух переменных допускает графическую иллюстрацию. Обычно график функции  есть поверхность в трехмерном пространстве (при этом область определения функции есть проекция этой поверхности на плоскость xOy).
есть поверхность в трехмерном пространстве (при этом область определения функции есть проекция этой поверхности на плоскость xOy).
Функции трех и большего числа переменных невозможно представить геометрически (в обычном трехмерном пространстве).
Заметим, что все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных  и мы будем в основном изучать именно их.
и мы будем в основном изучать именно их.
Непрерывность
Понятие непрерывности функции нескольких переменных определяется так же, как и для функции одной переменной.
Пусть  , пусть
, пусть 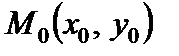 – некоторая точка. Придадим аргументам x и y приращения D x, D y (т.е. перейдем от
– некоторая точка. Придадим аргументам x и y приращения D x, D y (т.е. перейдем от 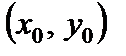 к
к  ). Тогда функция
). Тогда функция 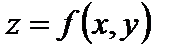 получит приращение D z. Если
получит приращение D z. Если
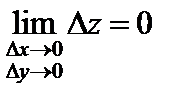 , (1)
, (1)
то говорят, что функция непрерывна в точке  . Иначе говоря, функция непрерывна, если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции*.
. Иначе говоря, функция непрерывна, если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции*.
Если учесть, что
 ,
,
и положить  ,
,  , то равенство (1) можно переписать в виде
, то равенство (1) можно переписать в виде
 . (2)
. (2)
Равенство (2) дает нам еще одно определение непрерывности: функция непрерывна, если ее предел равен ее значению от пределов аргументов.
Частные производные
Пусть 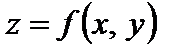 . Зафиксируем точку
. Зафиксируем точку 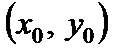 и, не меняя значения
и, не меняя значения  придадим аргументу x приращение D x, т.е. перейдем от
придадим аргументу x приращение D x, т.е. перейдем от 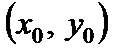 к
к 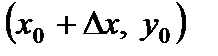 . Если существует предел
. Если существует предел
 ,
,
то этот предел называется частной производной функции 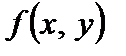 в точке
в точке 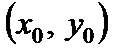 и обозначается одним из символов
и обозначается одним из символов
 ,
,  ,
,  ,
,  .
.
Аналогично определяется частная производная по y:
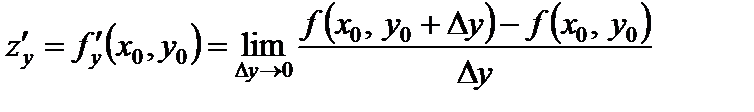 .
.
Таким образом, частная производная функции двух аргументов по одному из аргументов – это обычная производная той функции одного аргумента, которая получается из данной функции при фиксированном другом аргументе. (Поэтому, вычисляя, например,  , мы обращаемся с аргументом y как с константой.)
, мы обращаемся с аргументом y как с константой.)
Примеры. 1)  .
.
 ,
,  ;
;
2)  .
.
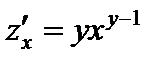 ,
,  .
.



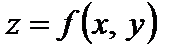 ,
,  ,
,  .
.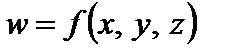 ,
,  и т.д.
и т.д. .
. есть функция двух переменных.
есть функция двух переменных. ,
, .
. , надо не только указать правило нахождения z по заданным x и y, но и то множество пар значений, которые могут принимать аргументы x и y. Это множество называется областью определения функции. В случае явного аналитического задания это множество определяется самой формулой, задающей функцию. Например, функция
, надо не только указать правило нахождения z по заданным x и y, но и то множество пар значений, которые могут принимать аргументы x и y. Это множество называется областью определения функции. В случае явного аналитического задания это множество определяется самой формулой, задающей функцию. Например, функция
 можно рассматривать как координаты точки на плоскости. В связи с этим мы можем сказать, что рассматриваемая функция задана на всей плоскости.
можно рассматривать как координаты точки на плоскости. В связи с этим мы можем сказать, что рассматриваемая функция задана на всей плоскости.
 , т.е. в круге радиуса R с центром в начале координат, ограниченном окружностью
, т.е. в круге радиуса R с центром в начале координат, ограниченном окружностью  (включая эту окружность).
(включая эту окружность).
 , т.е. в кольце, ограниченном окружностями радиусов
, т.е. в кольце, ограниченном окружностями радиусов  ,
,  , центр которого совпадает с началом координат (при этом точки, принадлежащие окружности
, центр которого совпадает с началом координат (при этом точки, принадлежащие окружности  принадлежат области определения, а точки окружности
принадлежат области определения, а точки окружности 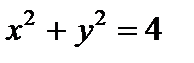 – не принадлежат).
– не принадлежат).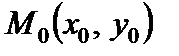 открытый круг радиуса e с центром в точке
открытый круг радиуса e с центром в точке  , т.е. множество точек
, т.е. множество точек 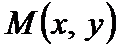 , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям .
. ,
,  ).
). есть поверхность в трехмерном пространстве (при этом область определения функции есть проекция этой поверхности на плоскость xOy).
есть поверхность в трехмерном пространстве (при этом область определения функции есть проекция этой поверхности на плоскость xOy). и мы будем в основном изучать именно их.
и мы будем в основном изучать именно их.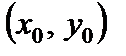 к
к  ). Тогда функция
). Тогда функция 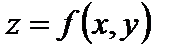 получит приращение D z. Если
получит приращение D z. Если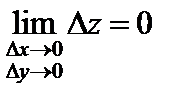 , (1)
, (1) . Иначе говоря, функция непрерывна, если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции*.
. Иначе говоря, функция непрерывна, если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции*. ,
, ,
,  , то равенство (1) можно переписать в виде
, то равенство (1) можно переписать в виде . (2)
. (2)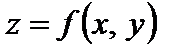 . Зафиксируем точку
. Зафиксируем точку 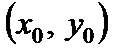 и, не меняя значения
и, не меняя значения  придадим аргументу x приращение D x, т.е. перейдем от
придадим аргументу x приращение D x, т.е. перейдем от 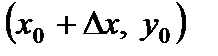 . Если существует предел
. Если существует предел ,
,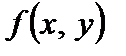 в точке
в точке  ,
,  ,
,  ,
,  .
.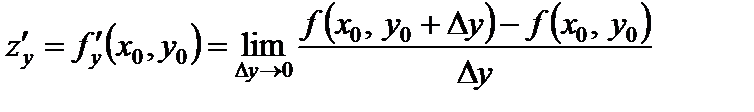 .
. .
. ,
,  ;
; .
.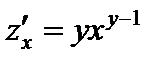 ,
,  .
.


