Лекция 1.Число. Переменная. Функция
Действительные числа. Числовая прямая
Напомним основные понятия, связанные с понятием действительного числа.
Натуральные числа – это целые положительные числа.
N – множество всех натуральных чисел:
N = {1, 2, 3,...}.
Z – множество всех целых чисел:
Z = {0, ±1, ±2, ±3,...}.
Рациональными числами называются числа вида 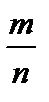 , где m – целое, n – натуральное.
, где m – целое, n – натуральное.
Q – множество всех рациональных чисел:  , если
, если  ,
, 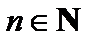 . Очевидно, что N Ì Z Ì Q.
. Очевидно, что N Ì Z Ì Q.
Числа, не являющиеся рациональными, называются иррациональными. Таковы, например,  ,
, 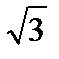 , число p. Обычно множество всех иррациональных чисел обозначают через I. Очевидно, множества I и Q не имеют общих элементов.
, число p. Обычно множество всех иррациональных чисел обозначают через I. Очевидно, множества I и Q не имеют общих элементов.
Множество Q всех рациональных чисел и множество I всех иррациональных чисел образуют множество R всех действительных чисел:
R = Q È I.
Геометрически множество всех действительных чисел изображается в виде числовой прямой (или числовой оси). Числовая прямая – это прямая, на которой выбраны: начало отсчета, положительное направление и масштаб (единичный отрезок).
Между множеством всех действительных чисел и множеством всех точек числовой прямой существует взаимно однозначное соответствие, т.е.
Каждому действительному числу соответствует одна определенная точка числовой прямой и, наоборот, каждой точке числовой прямой – одно определенное число. Поэтому понятия «число x» и «точка x» равнозначны.
Перечислим простейшие числовые множества на прямой. Пусть a и b – два числа, причем  .
.
Множество всех чисел, удовлетворяющих неравенству  , называется отрезком или сегментом [ a, b ].
, называется отрезком или сегментом [ a, b ].
Множество всех чисел, удовлетворяющих строгому неравенству 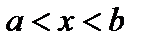 , называется интервалом (a, b).
, называется интервалом (a, b).
Полуинтервалы [ a, b) и (a, b ] определяются как множества чисел, удовлетворяющих соответственно неравенствам 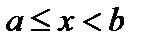 и
и  .
.
Аналогично определяются бесконечные интервалы и полуинтервалы  ,
,  ,
, 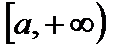 ,
,  . При этом вся числовая прямая есть
. При этом вся числовая прямая есть 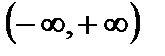 .
.
В дальнейшем для всех перечисленных множеств мы будем также применять общий термин «промежуток».
Модуль действительного числа
Модулем, или абсолютной величиной действительного числа x называется само число x, если x неотрицательно, и противоположное число, т.е. – x, если x отрицательно:
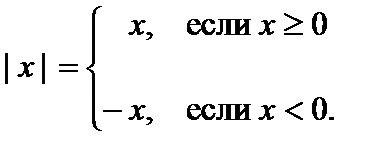
Очевидно, по определению,  .
.
Известны следующие свойства абсолютных величин:
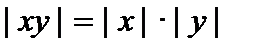
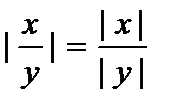

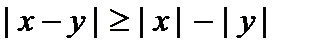 .
.
Модуль разности двух чисел  есть расстояние между точками x и a на числовой прямой (при любых x и a).
есть расстояние между точками x и a на числовой прямой (при любых x и a).
Из этого следует, что, в частности, решениями неравенства 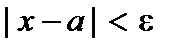 (где
(где  ) являются все точки x интервала
) являются все точки x интервала 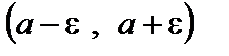 , т.е. числа, удовлетворяющие неравенству
, т.е. числа, удовлетворяющие неравенству  .
.
Такой интервал  называется e -окрестностью точки
называется e -окрестностью точки  . Заметим, что вообще окрестностью точки a называется всякий интервал, содержащий точку a.
. Заметим, что вообще окрестностью точки a называется всякий интервал, содержащий точку a.
Предел функции
Функция 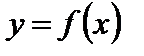 представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.
представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.
Сформулируем строгое определение предела функции. Пусть функция 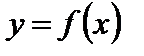 определена в некоторой окрестности точки a, кроме, может быть, точки a.
определена в некоторой окрестности точки a, кроме, может быть, точки a.
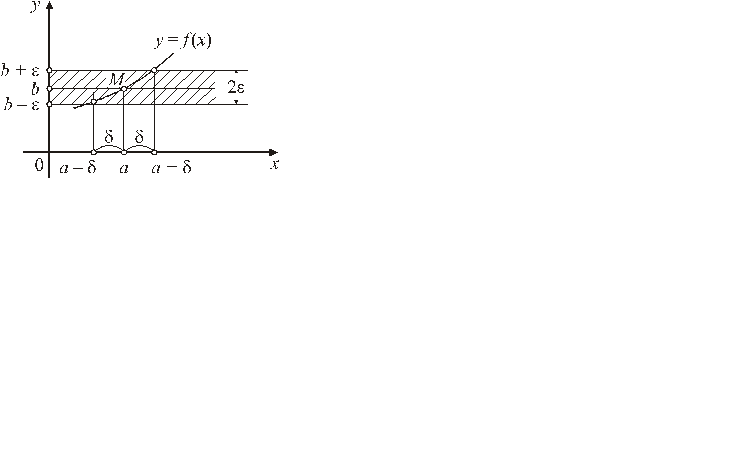
Определение 1. Число b называется пределом функции 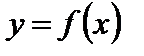 при x, стремящемся к a, если для любого (сколь угодно малого) числа
при x, стремящемся к a, если для любого (сколь угодно малого) числа 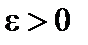 существует такое
существует такое 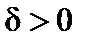 , что для всех x, отличных от a и удовлетворяющих неравенству
, что для всех x, отличных от a и удовлетворяющих неравенству
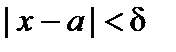 ,
,
выполняется неравенство
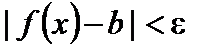 .
.
Если b есть предел 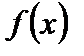 при
при 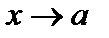 , то пишут
, то пишут
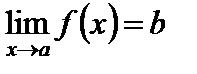 ,
,
или 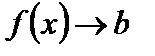 при
при 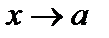 .
.
Дадим геометрическую иллюстрацию определения предела:
для всех точек 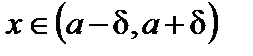 точки графика функции
точки графика функции 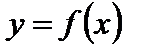 лежат внутри полосы, ограниченной прямыми
лежат внутри полосы, ограниченной прямыми 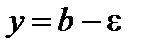 и
и 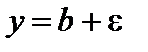 (рис. 11).
(рис. 11).
|
| Рис. 11
|
Замечание. Если 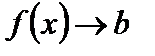 при
при 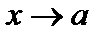 и при этом
и при этом  , то говорим, что
, то говорим, что 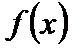 стремится к b слева, и пишем
стремится к b слева, и пишем 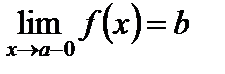 . Аналогично определяется предел справа:
. Аналогично определяется предел справа: 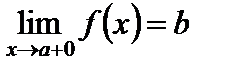 , если
, если 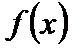 стремится к b, когда x стремится к a, оставаясь больше a. В частности, если
стремится к b, когда x стремится к a, оставаясь больше a. В частности, если 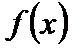 стремится к b при
стремится к b при 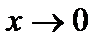 справа (соответственно слева), то пишем
справа (соответственно слева), то пишем 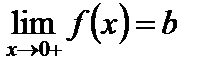 (соответственно
(соответственно 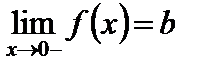 ).
).
Данное выше определение предела относилось к случаю, когда x стремится к конечному пределу а. Рассмотрим теперь случай 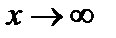 .
.
Определение 2. Число b есть предел функции 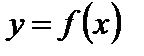 при
при 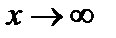 , если для любого (сколь угодно малого) числа
, если для любого (сколь угодно малого) числа 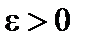 существует такое
существует такое 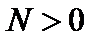 , что для всех x, удовлетворяющих неравенству
, что для всех x, удовлетворяющих неравенству 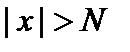 , выполняется неравенство
, выполняется неравенство
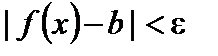 .
.
В этом случае пишем 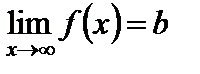 .
.
Если переменная величина является последовательностью, т.е. все ее значения можно занумеровать натуральными числами
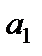 ,
, 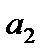 ,...,
,..., 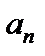 ,...,
,...,
то ее можно рассматривать как функцию натурального аргумента:
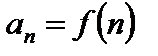 ,
, 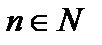 .
.
Определение 2 можно рассматривать, в частности, и как определение предела последовательности (если считать, что аргумент x принимает лишь целые положительные значения).
2.2. Бесконечно малые величины. Связь переменной
величины с ее пределом. Свойства бесконечно малых
Определение. Переменная величина называется бесконечно малой, если она стремится к нулю.
В частности, функция 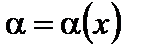 есть бесконечно малая при
есть бесконечно малая при 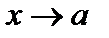 (или при
(или при 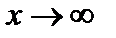 ), если
), если 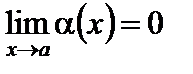 (соответственно,
(соответственно, 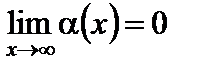 ).
).
Теорема. Число b есть предел переменной y тогда и только тогда, когда
(1) 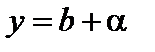 ,
,
где a – бесконечно малая.
Доказательство. 1. Необходимость. Пусть 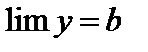 . Пусть задано
. Пусть задано 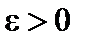 . Тогда для всех значений y, начиная с некоторого, будет
. Тогда для всех значений y, начиная с некоторого, будет 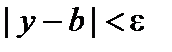 . Обозначим
. Обозначим 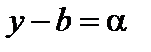 . Очевидно, для всех значений a, начиная с некоторого, будет
. Очевидно, для всех значений a, начиная с некоторого, будет 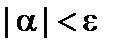 , следовательно, a – бесконечно малая. Итак,
, следовательно, a – бесконечно малая. Итак,
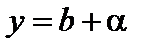 ,
,
где a – бесконечно малая.
2. Достаточность. Из равенства (1) следует 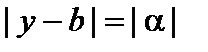 . Пусть задано
. Пусть задано 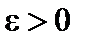 . Так как a – бесконечно малая, то для всех значений a, начиная с некоторого, будет
. Так как a – бесконечно малая, то для всех значений a, начиная с некоторого, будет 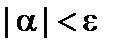 , следовательно, для всех значений y, начиная с некоторого, будет
, следовательно, для всех значений y, начиная с некоторого, будет 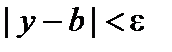 . А это значит, что
. А это значит, что 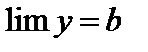 .
.
Теорема доказана.
Перечислим свойства бесконечно малых величин.
1. Если a – бесконечно малая и не обращается в нуль, то 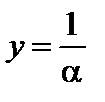 стремится к бесконечности.
стремится к бесконечности.
Заметим, что переменная величина, стремящаяся к бесконечности, называется бесконечно большой. Поэтому сформулированное выше свойство можно переформулировать так: величина, обратная бесконечно малой, есть бесконечно большая величина.
2. Алгебраическая сумма двух (трех и вообще конечного числа) бесконечно малых величин есть бесконечно малая.
Иначе говоря, если 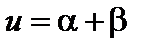 , где a, b – бесконечно малые, то и u – бесконечно малая.
, где a, b – бесконечно малые, то и u – бесконечно малая.
3. Произведение бесконечно малой величины на величину ограниченную есть величина бесконечно малая.
(Т. е. если a – бесконечно малая, z – ограниченная, то 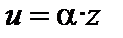 есть бесконечно малая.)
есть бесконечно малая.)
Следствие 1. Произведение двух бесконечно малых есть величина бесконечно малая.
Следствие 2. Если a – бесконечно малая, 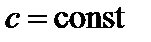 , то
, то 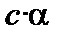 – бесконечно малая.
– бесконечно малая.
4. Если a– бесконечно малая, а переменная величина z имеет предел, отличный от нуля, то 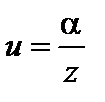 есть величина бесконечно малая.
есть величина бесконечно малая.
Следует заметить, что сформулированные свойства 1–4 являются, по существу, теоремами и в более подробном курсе математики излагаются с доказательствами. Здесь мы докажем одно из них, например свойство 3.
Пусть a– бесконечно малая, z – ограниченная величина, 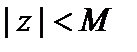 . Надо доказать, что
. Надо доказать, что 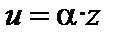 – бесконечно малая. Пусть задано
– бесконечно малая. Пусть задано 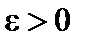 . Возьмем
. Возьмем  . Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет
. Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет 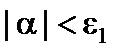 , т.е.
, т.е. 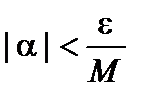 . Тогда
. Тогда 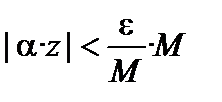 , т.е.
, т.е. 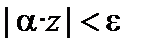 . Доказательство закончено.
. Доказательство закончено.
2.3. Предел суммы, произведения, частного.
Предельный переход в неравенствах
Мы будем рассматривать предел функций 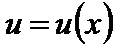 ,
, 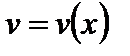 при
при 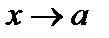 или при
или при 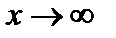 .
.
1. Предел алгебраической суммы конечного числа переменных равен алгебраической сумме пределов:
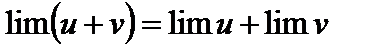 .
.
(Вообще 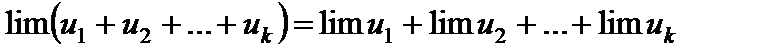 .)
.)
2. Предел произведения конечного числа переменных равен произведению пределов этих переменных:
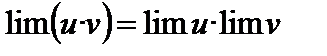 .
.
(Вообще 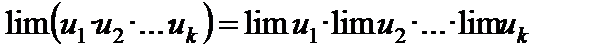 .)
.)
Следствие. Постоянный множитель можно выносить за знак предела: 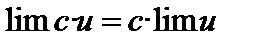 .
.
3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля:
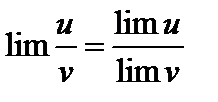 (если
(если 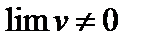 ).
).
Утверждения 1–3 также являются теоремами. Их доказательства основаны на теореме о связи переменной величины с ее пределом.
Приведем в качестве примера доказательство утверждения 2.
Пусть 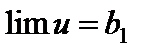 ,
, 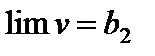 . Надо доказать, что
. Надо доказать, что 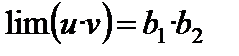 . Имеем:
. Имеем: 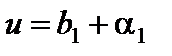 ,
, 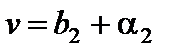 , где
, где 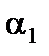 ,
, 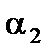 – бесконечно малые.
– бесконечно малые.
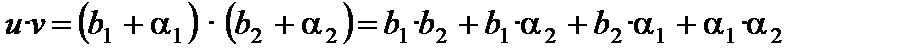 .
.
Обозначим 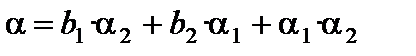 . В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как
. В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как 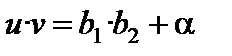 , где a – бесконечно малая, то
, где a – бесконечно малая, то 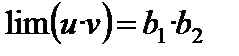 . Доказательство закончено.
. Доказательство закончено.
Можно доказать также следующие утверждения.
4. Если переменная y неотрицательна, то ее предел неотрицателен: если 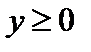 , то
, то 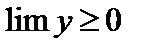 .
.
5. Если для переменных u и v выполняется неравенство 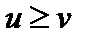 , то
, то 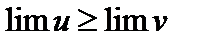 .
.
6. Если для переменных u, z и v выполняются неравенства 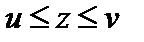 и при этом u и v стремятся к одному пределу b (
и при этом u и v стремятся к одному пределу b (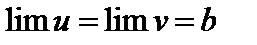 ), то переменная z стремится к тому же пределу:
), то переменная z стремится к тому же пределу: 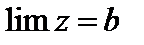 .
.
7. Достаточный признак существования предела: если переменная величина v возрастает и ограничена, т.е. 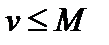 , то эта переменная величина имеет предел:
, то эта переменная величина имеет предел:
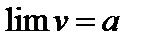 , где
, где 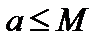 .
.
Аналогичное утверждение справедливо и для убывающей ограниченной величины.
Замечательные пределы
1. Предел функции 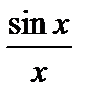 при
при 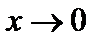 равен 1:
равен 1:
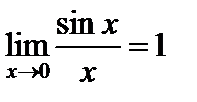 . (1)
. (1)
Рассмотрим примеры применения формулы (1).
Пример 1.
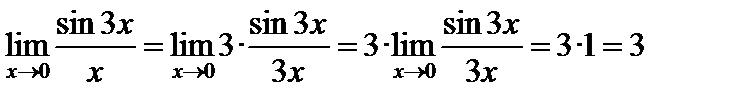 .
.
Пример 2.
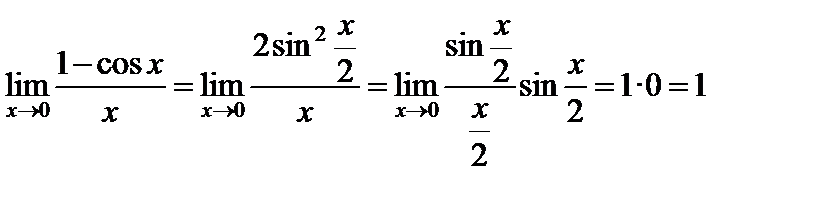 .
.
2. Предел переменной величины 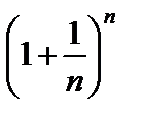 при
при 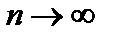 .
.
Теорема. Переменная величина 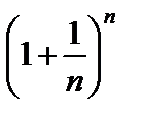 при
при 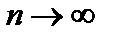 имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Доказательство этой теоремы основано на достаточном признаке существования предела, сформулированном выше.
Определение. Предел переменной величины 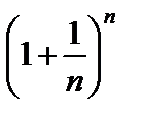 при
при 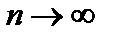 называется числом е:
называется числом е:
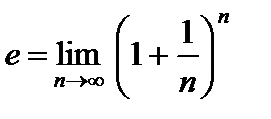 .
.
Заметим, что число e – иррациональное число
е = 2,7182818284...
(Обычно в вычислениях полагают 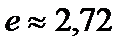 .)
.)
Можно доказать, что
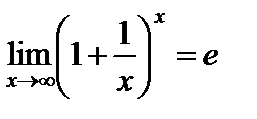 . (3)
. (3)
(В формуле (2) переменная 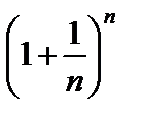 является последовательностью, в формуле (3) переменная
является последовательностью, в формуле (3) переменная 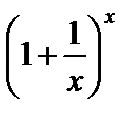 является функцией.)
является функцией.)
Сделав в формуле (3) замену 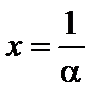 , получаем
, получаем
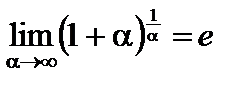 . (4)
. (4)
Примеры:
1) 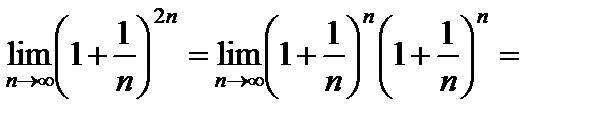
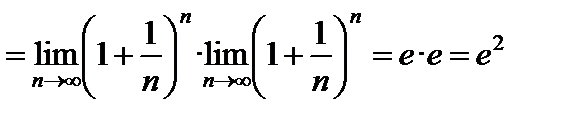 ;
;
2) 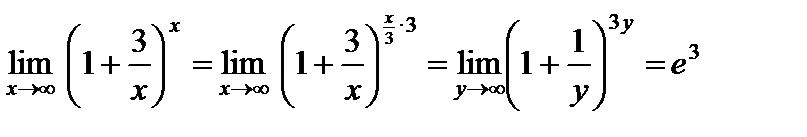 ;
;
3) 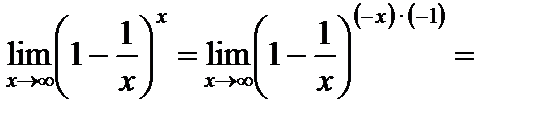
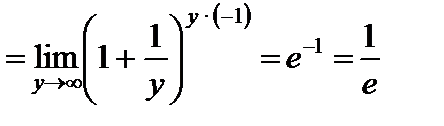 ;
;
4) 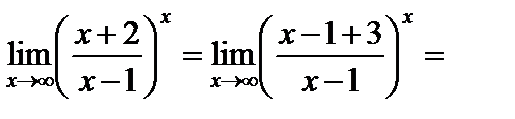
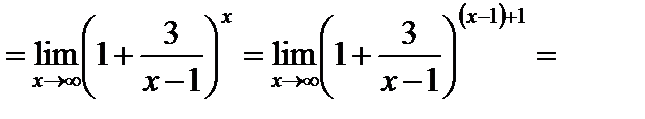
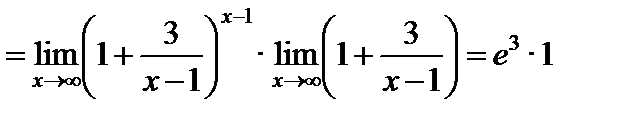 .
.
Число е играет очень важную роль в математике и ее приложениях.
Показательная функция с основанием е:
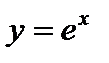
называется экспонентной.
Логарифмы с основанием е называют натуральными логарифмами и обозначают 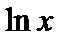 , т.е. вместо
, т.е. вместо 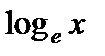 пишут
пишут 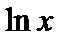 . Очевидно, если
. Очевидно, если 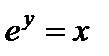 , то
, то 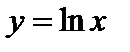 .
.
Непрерывность функций
Определение 1. Функция 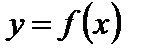 называется непрерывной в точке
называется непрерывной в точке 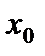 , если она определена в этой точке и в некоторой окрестности этой точки и если
, если она определена в этой точке и в некоторой окрестности этой точки и если
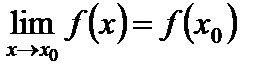 .
.
С геометрической точки зрения непрерывная функция – это функция, график которой есть непрерывная кривая. Существует несколько эквивалентных определений непрерывности.
Обозначим разность 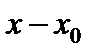 через
через 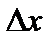 . Будем говорить, что при переходе от значения
. Будем говорить, что при переходе от значения 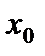 к значению x аргумент получает приращение
к значению x аргумент получает приращение 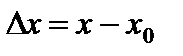 *. При этом функция y получает соответствующее приращение
*. При этом функция y получает соответствующее приращение 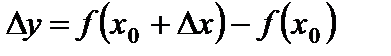 . С учетом сказанного, равенство (1) принимает вид:
. С учетом сказанного, равенство (1) принимает вид:
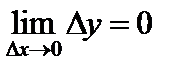 .
.
Определение. Функция 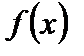 называется непрерывной в точке
называется непрерывной в точке 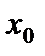 , если она определена в этой точке и некоторой ее окрестности и если
, если она определена в этой точке и некоторой ее окрестности и если
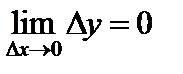 . (2)
. (2)
(Это определение легко запоминается в следующей форме: «функция непрерывна, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции».)
Пример. Покажем, что функция 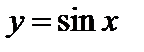 непрерывна в произвольной точке
непрерывна в произвольной точке 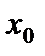 . Действительно, придадим аргументу приращение
. Действительно, придадим аргументу приращение 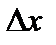 . Тогда функция получит приращение
. Тогда функция получит приращение
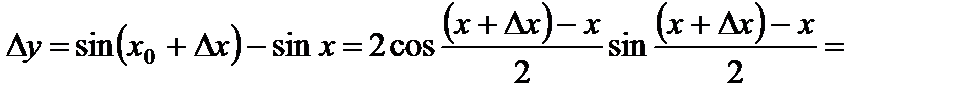
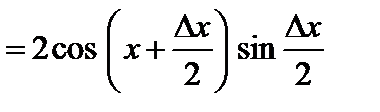 .
.
Если 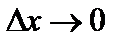 , то
, то 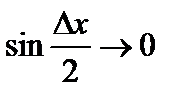 (так как
(так как 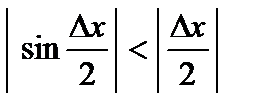 ); при этом
); при этом 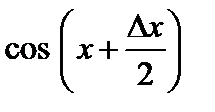 – ограничена. Поэтому
– ограничена. Поэтому
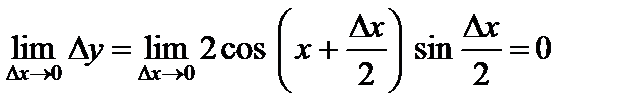 .
.
Следовательно, функция 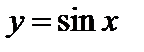 непрерывна.
непрерывна.
Аналогично можно доказать, что любая основная элементарная функция непрерывна в каждой точке, в которой она определена.
Справедливы следующие теоремы:
1. Если функции 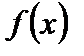 и
и 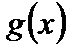 непрерывны в точке
непрерывны в точке 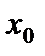 , то их сумма
, то их сумма 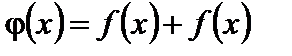 также непрерывна в этой точке.
также непрерывна в этой точке.
2. Произведение двух непрерывных функций есть непрерывная функция.
3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль (т.е. если 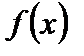 и
и 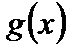 непрерывны в точке
непрерывны в точке 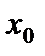 и
и 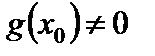 , то
, то 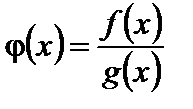 непрерывна в точке
непрерывна в точке 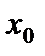 ).
).
4. Если 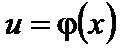 непрерывна при
непрерывна при 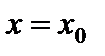 и
и 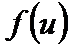 непрерывна в точке
непрерывна в точке 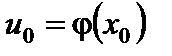 , то сложная функция
, то сложная функция 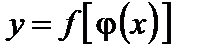 непрерывна в точке
непрерывна в точке 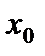 .
.
Доказательства этих утверждений основаны на свойствах пределов.
На этих утверждениях* основана следующая теорема.
Теорема. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Если функция 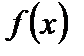 не является непрерывной в точке
не является непрерывной в точке 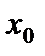 , то точка
, то точка 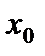 называется точкой разрыва функции
называется точкой разрыва функции 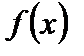 . Различают точки разрыва первого рода, когда существуют конечные пределы
. Различают точки разрыва первого рода, когда существуют конечные пределы 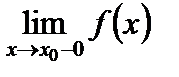 и
и 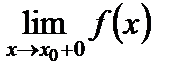 , но
, но 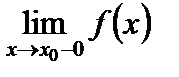 ¹
¹ 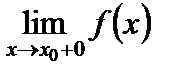 , и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции
, и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции 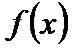 при
при 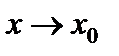 существует, но не равен
существует, но не равен 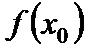 .
.
Примеры:
1) 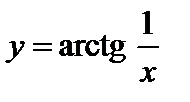 . Здесь
. Здесь 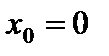 – точка разрыва первого рода, так как предел при
– точка разрыва первого рода, так как предел при 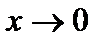 слева равен
слева равен 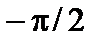 , а предел при
, а предел при 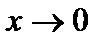 справа равен
справа равен 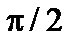 ;
;
2) 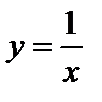 . Здесь
. Здесь 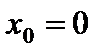 – точка разрыва второго рода;
– точка разрыва второго рода;
3) 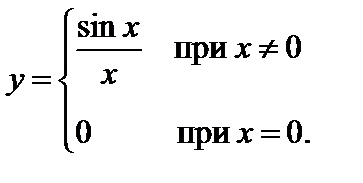 Здесь
Здесь 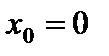 – точка устранимого разрыва, так как существует
– точка устранимого разрыва, так как существует 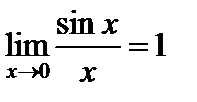 .
.
Определение 3. Если функция 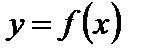 непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
Решение задач
1) 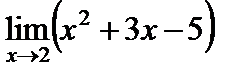
 ;
;
2)  ;
;
3)  ;
;
4)  ;
;
здесь теорема о пределе частного неприменима: и числитель, и знаменатель стремятся к нулю. Предел находят путем разложения числителя и знаменателя на множители:

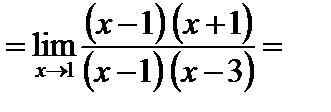
 .
.
(Здесь мы сократили дробь на множитель 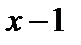 , который хотя и является бесконечно малой величиной при
, который хотя и является бесконечно малой величиной при 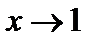 , но все же отличен от нуля:
, но все же отличен от нуля: 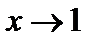 , но
, но  .)
.)
5)  ;
;
делим числитель и знаменатель на  и учитываем, что
и учитываем, что 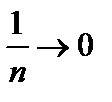 :
:
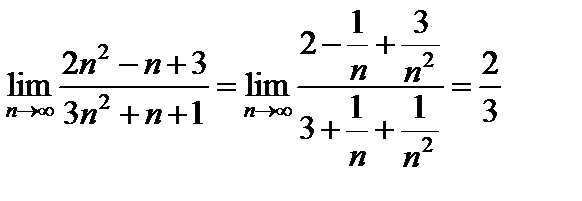 ;
;
6)  ;
;
7)  ;
;
умножим числитель и знаменатель на  :
:
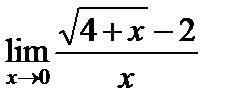
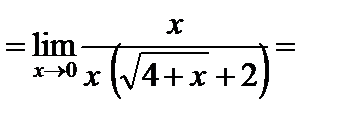
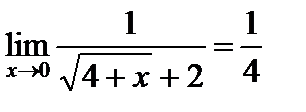 ;
;
8) 

 ;
;
9) 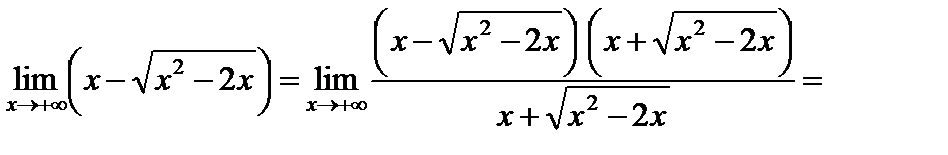
 ;
;
10) 
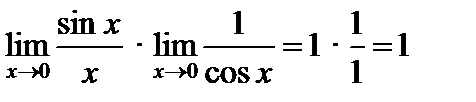 ;
;
11)  ;
;
12) 
 ;
;
13) 

 ;
;
Можно иначе:
 .
.
Лекция 3. Основы дифференциального
исчисления
Производная
Пусть функция  определена на некотором промежутке X. Придадим значению аргумента
определена на некотором промежутке X. Придадим значению аргумента  произвольное приращение
произвольное приращение  так, чтобы точка
так, чтобы точка 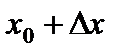 также принадлежала X. Тогда функция
также принадлежала X. Тогда функция 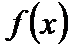 получит соответствующее приращение
получит соответствующее приращение 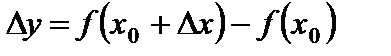 .
.
Определение. Производной функции  в точке
в точке 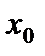 называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при  (если этот предел существует):
(если этот предел существует):
 .
.
Производная имеет несколько обозначений: 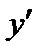 ,
, 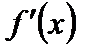 ,
, 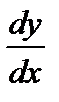 . Иногда в обозначении производной используется индекс, указывающий по какой переменной взята производная, например,
. Иногда в обозначении производной используется индекс, указывающий по какой переменной взята производная, например,  .
.
Если функция в точке 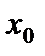 имеет конечную производную, то функция называется дифференцируемой в этой точке. Нахождение производной называется дифференцированием.
имеет конечную производную, то функция называется дифференцируемой в этой точке. Нахождение производной называется дифференцированием.
Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке. В этом случае  также является функцией от аргумента x, определенной на этом промежутке.
также является функцией от аргумента x, определенной на этом промежутке.
Мгновенная скорость
Пусть функция 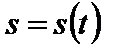 описывает закон движения материальной точки по прямой (как зависимость пути s от времени t). Тогда за промежуток времени
описывает закон движения материальной точки по прямой (как зависимость пути s от времени t). Тогда за промежуток времени  пройденный путь равен
пройденный путь равен 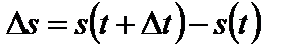 . Отношение
. Отношение 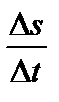 есть средняя скорость за время
есть средняя скорость за время  . А тогда
. А тогда

есть мгновенная скорость в момент времени t. Итак, мгновенная скорость есть производная пути по времени.
Пример. Пусть x – количество вещества, образовавшегося при химической реакции к моменту времени t. Очевидно, x есть функция времени:  . Если t получает приращение
. Если t получает приращение 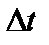 , то x получает соответствующее приращение
, то x получает соответствующее приращение  . Тогда отношение
. Тогда отношение 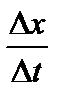 представляет собой среднюю скорость химической реакции за время с момента t до момента
представляет собой среднюю скорость химической реакции за время с момента t до момента  , а предел этого отношения при
, а предел этого отношения при 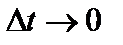 , т.е.
, т.е.  – скорость химической реакции в момент t.
– скорость химической реакции в момент t.
Связь между дифференцируемостью
и непрерывностью
Теорема. Если функция дифференцируема в точке 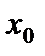 , то она и непрерывна в этой точке.
, то она и непрерывна в этой точке.
Доказательство. Пусть  дифференцируема в данной точке, т.е. существует предел
дифференцируема в данной точке, т.е. существует предел
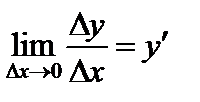 .
.
Тогда  , где a – бесконечно малая. Отсюда
, где a – бесконечно малая. Отсюда
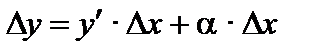 .
.
Пусть 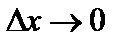 . Тогда
. Тогда
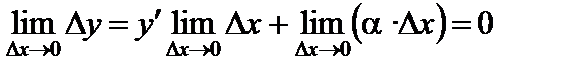 .
.
Итак, бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. функция непрерывна.
Теорема доказана.
Обратное утверждение неверно: функция, непрерывная в точке, может не иметь производной в этой точке.
Правила дифференцирования
Пусть  ,
, 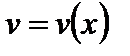 – дифференцируемые функции, c – константа. Тогда:
– дифференцируемые функции, c – константа. Тогда:
I. 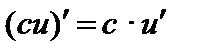 (постоянный множитель выносится за знак производной).
(постоянный множитель выносится за знак производной).
II.  (производная алгебраической суммы равна алгебраической сумме производных).
(производная алгебраической суммы равна алгебраической сумме производных).
III. 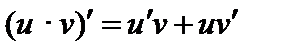 .
.
IV.  .
.
V. Если  ,
,  , то
, то
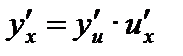 .
.
Докажем в качестве примера правило III.
1. Дадим x приращение 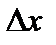 . Тогда функции u и v получают значения
. Тогда функции u и v получают значения 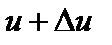 ,
, 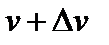 , а функция
, а функция  – значение
– значение 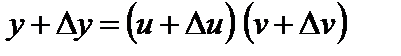 .
.
2. Найдем приращение функции
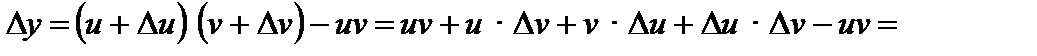

3. Состав отношение 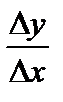 :
:
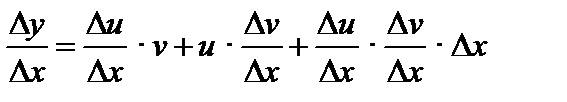 .
.
4. Вычислим предел при  :
:


 .
.
Итак,  .
.
Таблица производных
1. 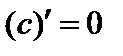 .
.
2.  .
.
3. 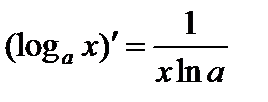 .
.
 .
.
4. 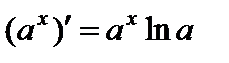 .
.
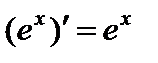 .
.
5. 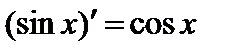 .
.
6.  .
.
7.  .
.
8.  .
.
9. 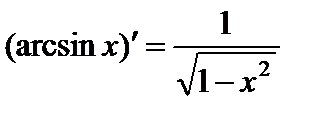 .
.
10.  .
.
11.  .
.
12.  .
.
Схему доказательства формулы 2 мы рассмотрели ранее. Докажем еще в качестве примера формулы 5 и 7.
Пусть 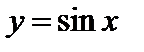 . Придадим x приращение
. Придадим x приращение  . Получаем
. Получаем
 =
=
 .
.
Составим отношение
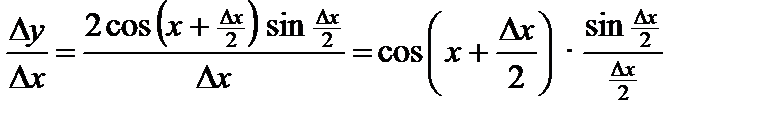 .
.
Перейдем к пределу при 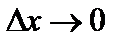 :
:

Пусть  . Применим правило дифференцирования дроби:
. Применим правило дифференцирования дроби:

Приведем теперь примеры вычисления производных с применением формул и правил дифференцирования.
1) 
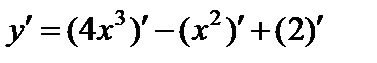
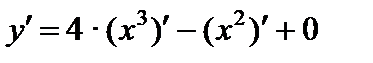
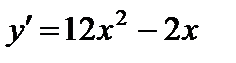 ;
;
2) 
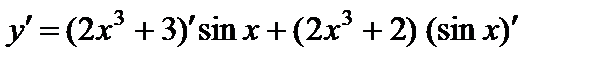
 ;
;
3) 



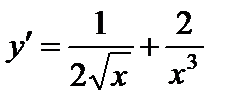 ;
;
4) 
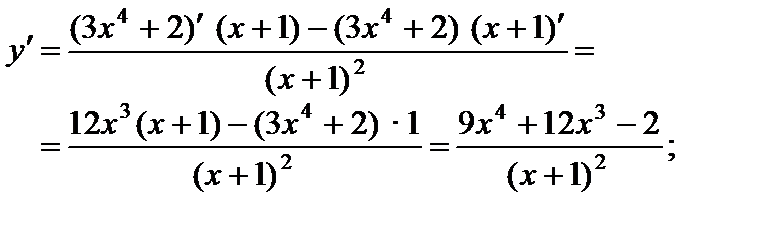
5) 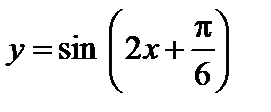
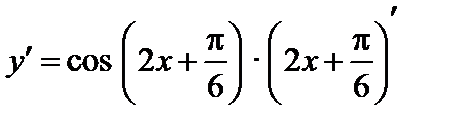
 ;
;
6) 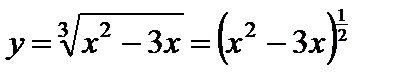
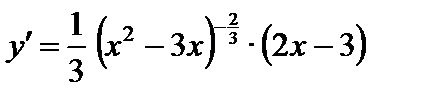

Дифференциал
Пусть функция  имеет в некоторой точке x производную
имеет в некоторой точке x производную 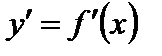 .
.
В соответствии с определением производной
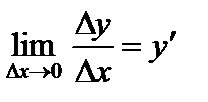
Отсюда
 ,
,
где a – бесконечно малая при 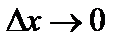 . Выразим
. Выразим  :
:
 .
.
Если 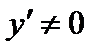 , то в правой части этого равенства первое слагаемое при малых
, то в правой части этого равенства первое слагаемое при малых 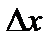 более важно, чем второе*. Это первое слагаемое (уже независимо от того, будет ли
более важно, чем второе*. Это первое слагаемое (уже независимо от того, будет ли  ) называют дифференциалом. Сформулируем понятие дифференциала более точно.
) называют дифференциалом. Сформулируем понятие дифференциала более точно.
Определение. Дифференциалом функции 
|
|
|



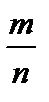 , где m – целое, n – натуральное.
, где m – целое, n – натуральное. , если
, если  ,
,  . Очевидно, что N Ì Z Ì Q.
. Очевидно, что N Ì Z Ì Q. ,
, 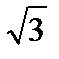 , число p. Обычно множество всех иррациональных чисел обозначают через I. Очевидно, множества I и Q не имеют общих элементов.
, число p. Обычно множество всех иррациональных чисел обозначают через I. Очевидно, множества I и Q не имеют общих элементов. .
. , называется отрезком или сегментом [ a, b ].
, называется отрезком или сегментом [ a, b ].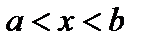 , называется интервалом (a, b).
, называется интервалом (a, b).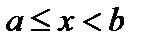 и
и  .
. ,
,  ,
, 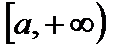 ,
,  . При этом вся числовая прямая есть
. При этом вся числовая прямая есть 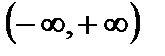 .
.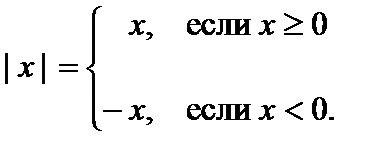
 .
.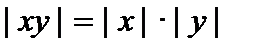
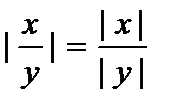

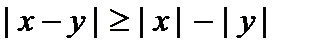 .
. есть расстояние между точками x и a на числовой прямой (при любых x и a).
есть расстояние между точками x и a на числовой прямой (при любых x и a).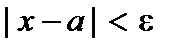 (где
(где  ) являются все точки x интервала
) являются все точки x интервала 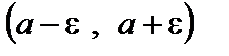 , т.е. числа, удовлетворяющие неравенству
, т.е. числа, удовлетворяющие неравенству  .
. называется e -окрестностью точки
называется e -окрестностью точки  . Заметим, что вообще окрестностью точки a называется всякий интервал, содержащий точку a.
. Заметим, что вообще окрестностью точки a называется всякий интервал, содержащий точку a.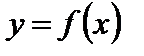 представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.
представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.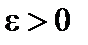 существует такое
существует такое 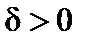 , что для всех x, отличных от a и удовлетворяющих неравенству
, что для всех x, отличных от a и удовлетворяющих неравенству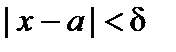 ,
,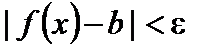 .
.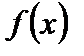 при
при 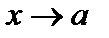 , то пишут
, то пишут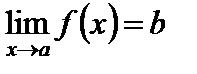 ,
,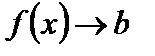 при
при 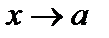 .
.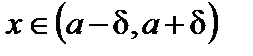 точки графика функции
точки графика функции 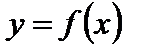 лежат внутри полосы, ограниченной прямыми
лежат внутри полосы, ограниченной прямыми 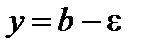 и
и 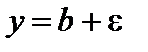 (рис. 11).
(рис. 11).
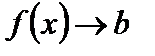 при
при 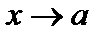 и при этом
и при этом  , то говорим, что
, то говорим, что 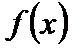 стремится к b слева, и пишем
стремится к b слева, и пишем 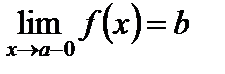 . Аналогично определяется предел справа:
. Аналогично определяется предел справа: 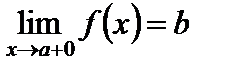 , если
, если 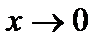 справа (соответственно слева), то пишем
справа (соответственно слева), то пишем 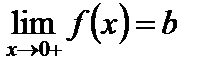 (соответственно
(соответственно 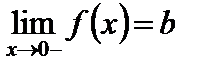 ).
).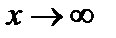 .
.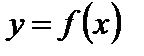 при
при 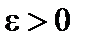 существует такое
существует такое 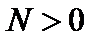 , что для всех x, удовлетворяющих неравенству
, что для всех x, удовлетворяющих неравенству 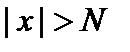 , выполняется неравенство
, выполняется неравенство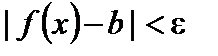 .
.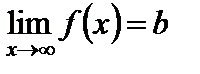 .
. ,
, 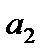 ,...,
,..., 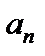 ,...,
,...,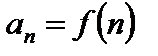 ,
, 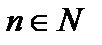 .
.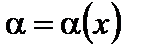 есть бесконечно малая при
есть бесконечно малая при 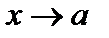 (или при
(или при 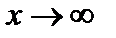 ), если
), если 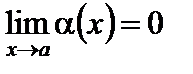 (соответственно,
(соответственно, 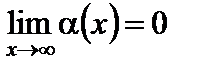 ).
).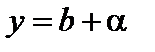 ,
,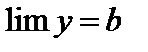 . Пусть задано
. Пусть задано 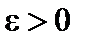 . Тогда для всех значений y, начиная с некоторого, будет
. Тогда для всех значений y, начиная с некоторого, будет 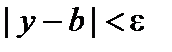 . Обозначим
. Обозначим 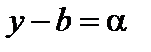 . Очевидно, для всех значений a, начиная с некоторого, будет
. Очевидно, для всех значений a, начиная с некоторого, будет 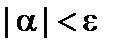 , следовательно, a – бесконечно малая. Итак,
, следовательно, a – бесконечно малая. Итак,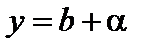 ,
,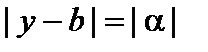 . Пусть задано
. Пусть задано 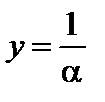 стремится к бесконечности.
стремится к бесконечности.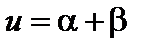 , где a, b – бесконечно малые, то и u – бесконечно малая.
, где a, b – бесконечно малые, то и u – бесконечно малая.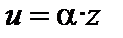 есть бесконечно малая.)
есть бесконечно малая.)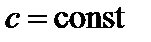 , то
, то 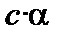 – бесконечно малая.
– бесконечно малая.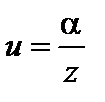 есть величина бесконечно малая.
есть величина бесконечно малая.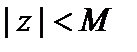 . Надо доказать, что
. Надо доказать, что 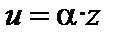 – бесконечно малая. Пусть задано
– бесконечно малая. Пусть задано 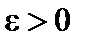 . Возьмем
. Возьмем  . Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет
. Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет 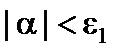 , т.е.
, т.е. 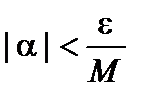 . Тогда
. Тогда 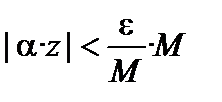 , т.е.
, т.е. 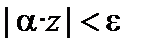 . Доказательство закончено.
. Доказательство закончено.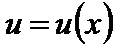 ,
, 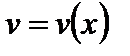 при
при 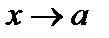 или при
или при 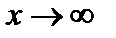 .
.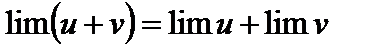 .
.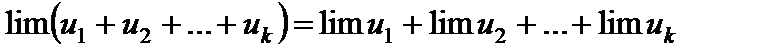 .)
.)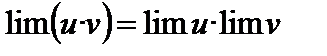 .
.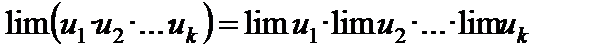 .)
.)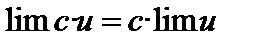 .
.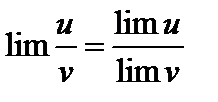 (если
(если 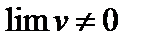 ).
).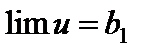 ,
, 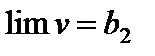 . Надо доказать, что
. Надо доказать, что 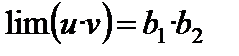 . Имеем:
. Имеем: 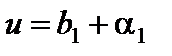 ,
, 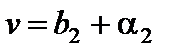 , где
, где 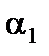 ,
, 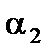 – бесконечно малые.
– бесконечно малые.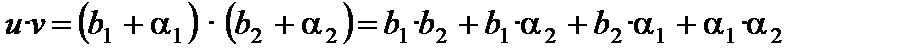 .
.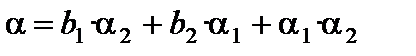 . В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как
. В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как 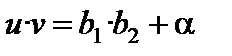 , где a – бесконечно малая, то
, где a – бесконечно малая, то 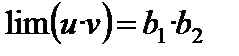 . Доказательство закончено.
. Доказательство закончено.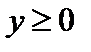 , то
, то 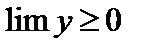 .
.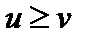 , то
, то 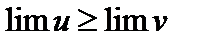 .
.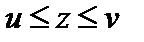 и при этом u и v стремятся к одному пределу b (
и при этом u и v стремятся к одному пределу b (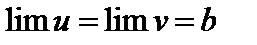 ), то переменная z стремится к тому же пределу:
), то переменная z стремится к тому же пределу: 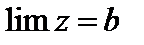 .
.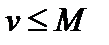 , то эта переменная величина имеет предел:
, то эта переменная величина имеет предел: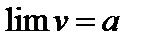 , где
, где 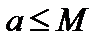 .
.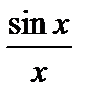 при
при 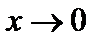 равен 1:
равен 1: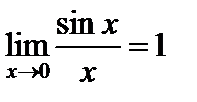 . (1)
. (1)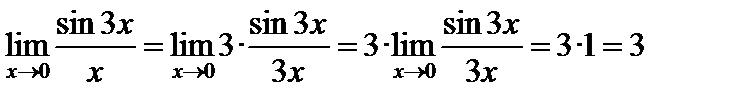 .
.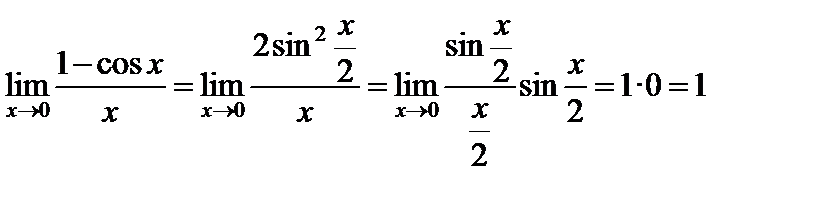 .
.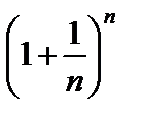 при
при 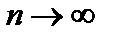 .
.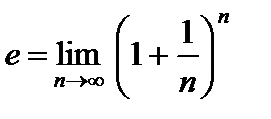 .
.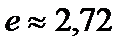 .)
.)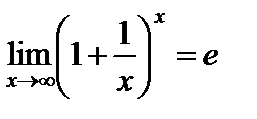 . (3)
. (3)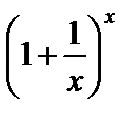 является функцией.)
является функцией.)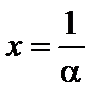 , получаем
, получаем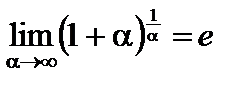 . (4)
. (4)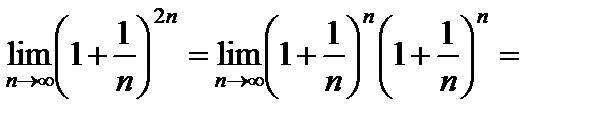
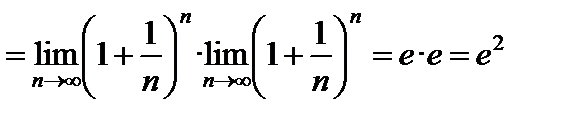 ;
;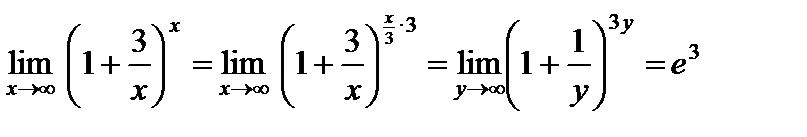 ;
;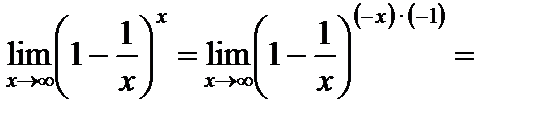
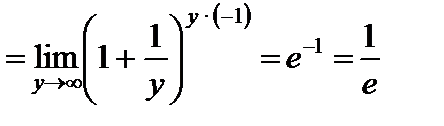 ;
;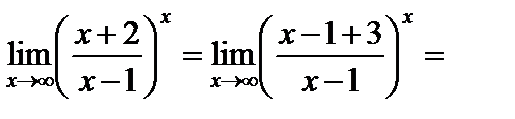
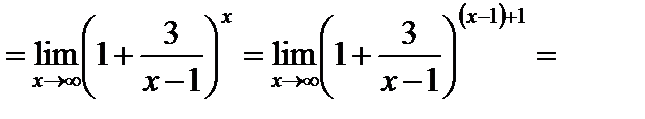
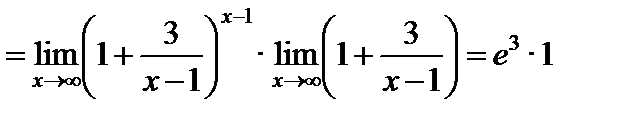 .
.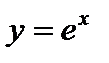
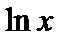 , т.е. вместо
, т.е. вместо 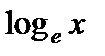 пишут
пишут 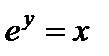 , то
, то 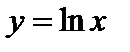 .
.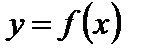 называется непрерывной в точке
называется непрерывной в точке 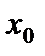 , если она определена в этой точке и в некоторой окрестности этой точки и если
, если она определена в этой точке и в некоторой окрестности этой точки и если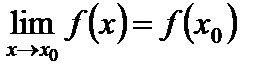 .
.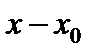 через
через 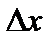 . Будем говорить, что при переходе от значения
. Будем говорить, что при переходе от значения 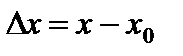 *. При этом функция y получает соответствующее приращение
*. При этом функция y получает соответствующее приращение 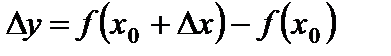 . С учетом сказанного, равенство (1) принимает вид:
. С учетом сказанного, равенство (1) принимает вид: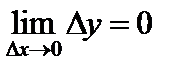 .
.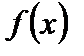 называется непрерывной в точке
называется непрерывной в точке 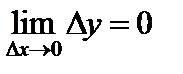 . (2)
. (2)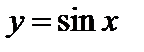 непрерывна в произвольной точке
непрерывна в произвольной точке 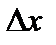 . Тогда функция получит приращение
. Тогда функция получит приращение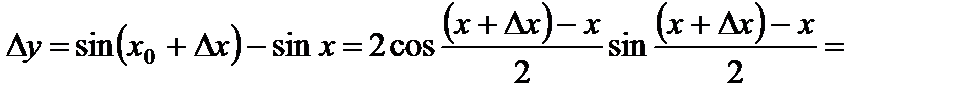
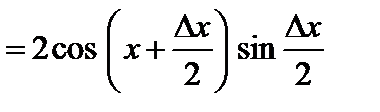 .
.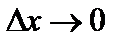 , то
, то 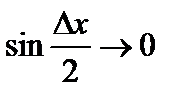 (так как
(так как 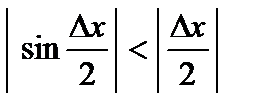 ); при этом
); при этом 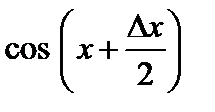 – ограничена. Поэтому
– ограничена. Поэтому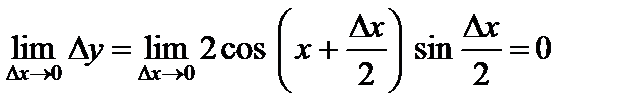 .
.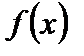 и
и 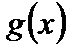 непрерывны в точке
непрерывны в точке  также непрерывна в этой точке.
также непрерывна в этой точке.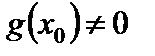 , то
, то 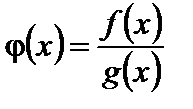 непрерывна в точке
непрерывна в точке 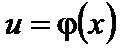 непрерывна при
непрерывна при 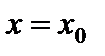 и
и 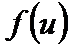 непрерывна в точке
непрерывна в точке 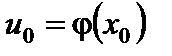 , то сложная функция
, то сложная функция 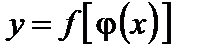 непрерывна в точке
непрерывна в точке 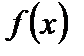 не является непрерывной в точке
не является непрерывной в точке 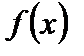 . Различают точки разрыва первого рода, когда существуют конечные пределы
. Различают точки разрыва первого рода, когда существуют конечные пределы 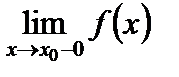 и
и 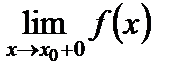 , но
, но 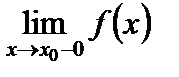 ¹
¹ 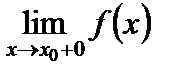 , и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции
, и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции 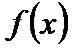 при
при 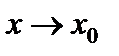 существует, но не равен
существует, но не равен 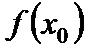 .
.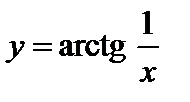 . Здесь
. Здесь 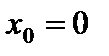 – точка разрыва первого рода, так как предел при
– точка разрыва первого рода, так как предел при 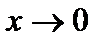 слева равен
слева равен 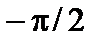 , а предел при
, а предел при 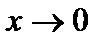 справа равен
справа равен 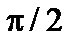 ;
;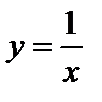 . Здесь
. Здесь  – точка разрыва второго рода;
– точка разрыва второго рода;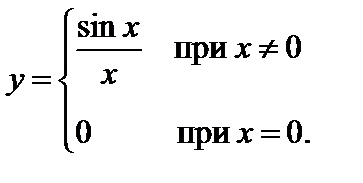 Здесь
Здесь  – точка устранимого разрыва, так как существует
– точка устранимого разрыва, так как существует 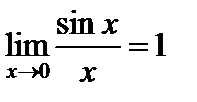 .
. непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.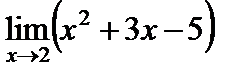
 ;
; ;
; ;
; ;
;
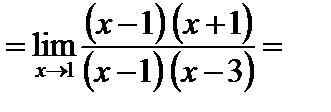
 .
.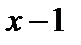 , который хотя и является бесконечно малой величиной при
, который хотя и является бесконечно малой величиной при 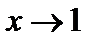 , но все же отличен от нуля:
, но все же отличен от нуля:  .)
.) ;
; и учитываем, что
и учитываем, что 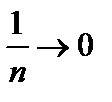 :
: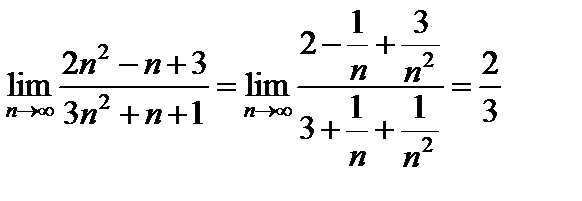 ;
; ;
; ;
; :
: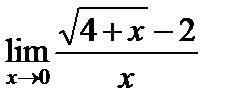
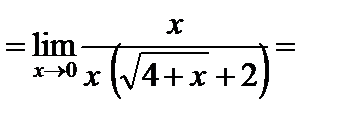
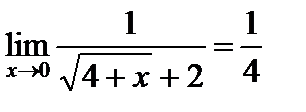 ;
;

 ;
;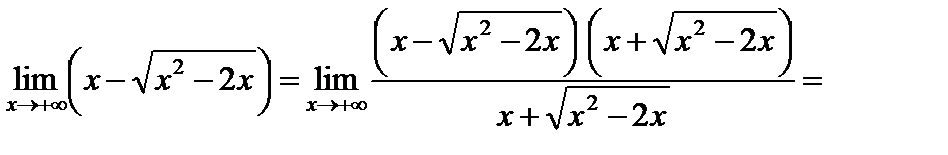
 ;
;
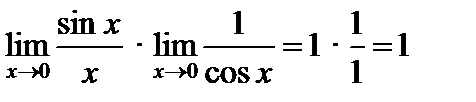 ;
; ;
;
 ;
;

 ;
; .
. определена на некотором промежутке X. Придадим значению аргумента
определена на некотором промежутке X. Придадим значению аргумента  произвольное приращение
произвольное приращение  так, чтобы точка
так, чтобы точка 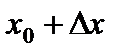 также принадлежала X. Тогда функция
также принадлежала X. Тогда функция 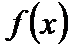 получит соответствующее приращение
получит соответствующее приращение 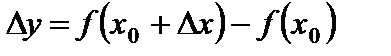 .
. (если этот предел существует):
(если этот предел существует): .
.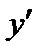 ,
, 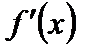 ,
, 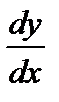 . Иногда в обозначении производной используется индекс, указывающий по какой переменной взята производная, например,
. Иногда в обозначении производной используется индекс, указывающий по какой переменной взята производная, например,  .
. также является функцией от аргумента x, определенной на этом промежутке.
также является функцией от аргумента x, определенной на этом промежутке.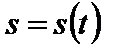 описывает закон движения материальной точки по прямой (как зависимость пути s от времени t). Тогда за промежуток времени
описывает закон движения материальной точки по прямой (как зависимость пути s от времени t). Тогда за промежуток времени  пройденный путь равен
пройденный путь равен 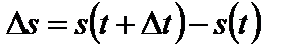 . Отношение
. Отношение 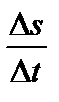 есть средняя скорость за время
есть средняя скорость за время  . А тогда
. А тогда
 . Если t получает приращение
. Если t получает приращение 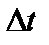 , то x получает соответствующее приращение
, то x получает соответствующее приращение  . Тогда отношение
. Тогда отношение 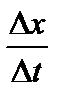 представляет собой среднюю скорость химической реакции за время с момента t до момента
представляет собой среднюю скорость химической реакции за время с момента t до момента  , а предел этого отношения при
, а предел этого отношения при 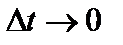 , т.е.
, т.е.  – скорость химической реакции в момент t.
– скорость химической реакции в момент t. дифференцируема в данной точке, т.е. существует предел
дифференцируема в данной точке, т.е. существует предел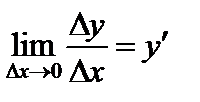 .
. , где a – бесконечно малая. Отсюда
, где a – бесконечно малая. Отсюда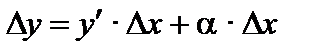 .
. . Тогда
. Тогда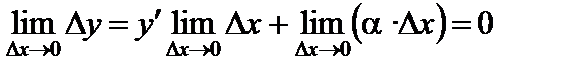 .
. ,
, 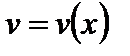 – дифференцируемые функции, c – константа. Тогда:
– дифференцируемые функции, c – константа. Тогда: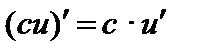 (постоянный множитель выносится за знак производной).
(постоянный множитель выносится за знак производной). (производная алгебраической суммы равна алгебраической сумме производных).
(производная алгебраической суммы равна алгебраической сумме производных).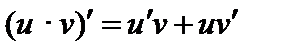 .
. .
. ,
,  , то
, то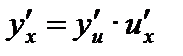 .
.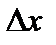 . Тогда функции u и v получают значения
. Тогда функции u и v получают значения 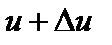 ,
, 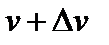 , а функция
, а функция  – значение
– значение 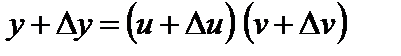 .
.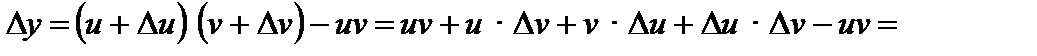

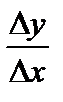 :
: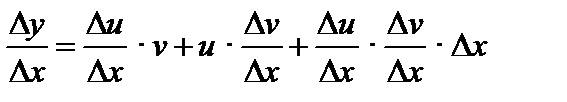 .
. :
:

 .
. .
.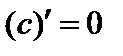 .
. .
.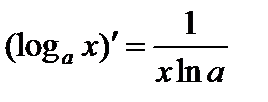 .
. .
.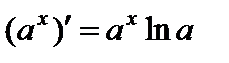 .
.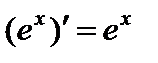 .
.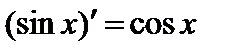 .
. .
. .
. .
.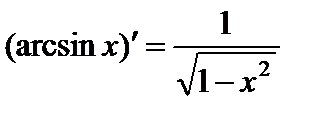 .
. .
. .
. .
. . Придадим x приращение
. Придадим x приращение  . Получаем
. Получаем =
= .
.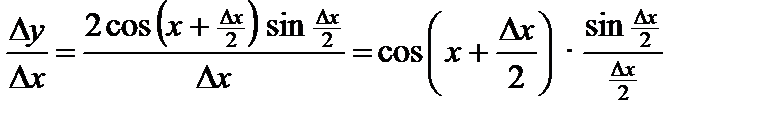 .
.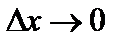 :
:
 . Применим правило дифференцирования дроби:
. Применим правило дифференцирования дроби:

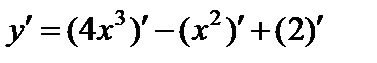
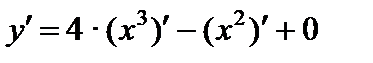
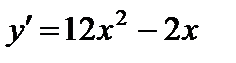 ;
;
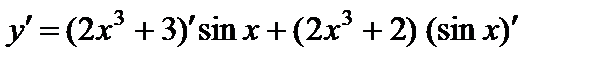
 ;
;



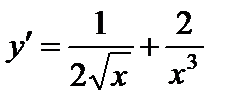 ;
;
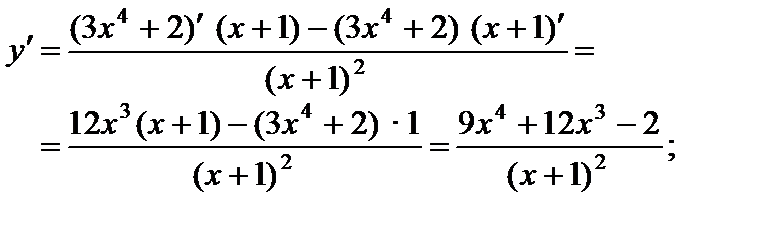
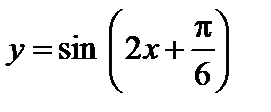
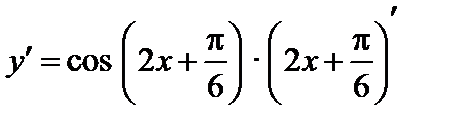
 ;
;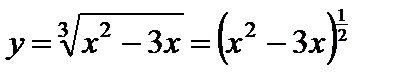
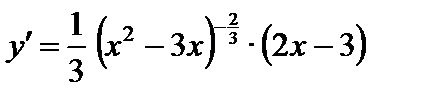

 имеет в некоторой точке x производную
имеет в некоторой точке x производную 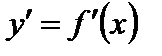 .
.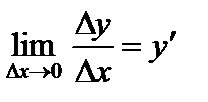
 ,
,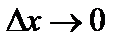 . Выразим
. Выразим  :
: .
.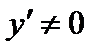 , то в правой части этого равенства первое слагаемое при малых
, то в правой части этого равенства первое слагаемое при малых 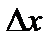 более важно, чем второе*. Это первое слагаемое (уже независимо от того, будет ли
более важно, чем второе*. Это первое слагаемое (уже независимо от того, будет ли  ) называют дифференциалом. Сформулируем понятие дифференциала более точно.
) называют дифференциалом. Сформулируем понятие дифференциала более точно.