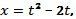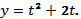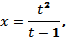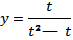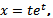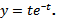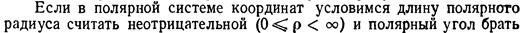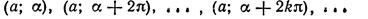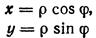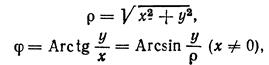Если уравнение кривой F(x, y) = 0 не меняется при замене х на –х, то кривая симметрична относительно оси ординат.
Если уравнение кривой F(x, y) = 0 не меняется при замене у на – у, то кривая симметрична относительно оси абсцисс.
Если уравнение кривой F(x,y)=0 не меняется при одновременной замене х на –х и у на – у, то кривая симметрична относительно начала координат.
Если уравнение кривой F(x,y)=0 не меняется при замене у на х, а х на у, то кривая симметрична относительно биссектрисы у=х.
Точки пересечения кривой F(х, у)=0 с осями координат. Точки пересечения с осью абсцисс — это решения системы уравнений
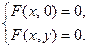
Точки пересечения с осью ординат — это решения системы уравнений
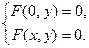
Другие точки графика.
Для более точного построения графика кривой F (x, у) иногда полезно найти отдельные точки этой кривой, не лежащие на координатных осях. Такие дополнительные точки целесообразно искать как точки пересечения кривой с прямыми у=kx при различных значениях k.
Если уравнения кривой F(х, у)=0 можно преобразовать к виду
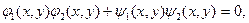
то координаты точек пересечения, кривых
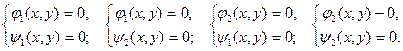
удовлетворяют уравнению начальной кривой и, следовательно, принадлежат ей.
Асимптоты кривой F(х, у)=0.
Для нахождения горизонтальных асимптот кривой F(х, у)= 0 приравнивают нулю коэффициент при высшей степени х, входящей в уравнение; причем если этот коэффициент — постоянная величина, то горизонтальных асимптот нет.
Для нахождения вертикальных асимптот кривой F(х, у)= 0 приравнивают нулю коэффициент при высшей степени у, входящей в уравнение этой кривой.
Для нахождения наклонных асимптот кривой F(х, у)= 0 надо в уравнении кривой заменить у на kx + b, приравнять нулю коэффициенты при двух высших степенях х и полученную систему решить относительно k и b.
Параметрически заданная функция.
Функция задана параметрически, если каждая координата x и y является функцией некоторой переменной t
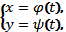
где t – параметр, 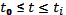 .
.
В этом случае исследование и построение графика функции проводятся также, как для функции, заданной уравнением 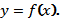 Сначала строят графики функций
Сначала строят графики функций 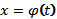 и
и 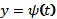 соответственно в системах координат
соответственно в системах координат 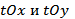 . Учитывая графическое изображение функций
. Учитывая графическое изображение функций 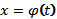 и
и 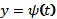 , исследуют функцию
, исследуют функцию 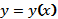 .
.
Особенности параметрически заданных функций и их графическое отображение.
График симметричен относительно оси ординат Oy, если при замене переменной t на –t не меняется значение у, а х переходит в –х.
График функции симметричен относительно оси абсцисс, если при замене переменной t на –t не меняется значение х, а у переходит в –у;
Период функции определяется по периодам функций 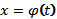 и
и 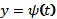 .
.
Точки пересечения с осями координат.
Для нахождения точек пересечения графика функции с осью абсцисс надо найти те значения t, при которых у=0 (решаем уравнение 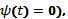 и находим соответствующее значение
и находим соответствующее значение 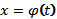 ; аналогично находим точки пересечения с осью ординат.
; аналогично находим точки пересечения с осью ординат.
Другие точки графика.
Иногда целесообразно определять точки пересечения графика с биссектрисами координатных углов у=х и у= -х, для чего решают соответственно уравнения
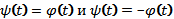 ,
,
откуда находят значения t и для них значения функций 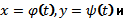 , которые при найденных t и дадут координаты искомых точек.
, которые при найденных t и дадут координаты искомых точек.
В простейших случаях можно строить графики параметрически заданных функций по точкам.
Задания.
№ 1. Исследовать асимптоты кривой
- х2у2 + у4 — 16 х2 = 0.
Решение.
Переписываем уравнение в виде
(у2 — 16) х2 + у4 = 0.
Приравниваем нулю коэффициент при х2:
у2 — 16 = 0,
откуда у – 4 = 0 и у + 4 = 0 — горизонтальные асимптоты рассматриваемой кривой.
- Зу2 — ху2 — 5 х2у = 0
Решение.
Действительно, переписываем уравнение в виде
(З — х)у2 — 5 х2у = 0,
откуда 3 — х = 0 вертикальная асимптота, у= 0 - горизонтальная асимптота.
- х3 + у3 – 3х2 = 0
Решение.
Ищем наклонные асимптоты.
заменяем в уравнении кривой у на kx + b:
х3 + (kx + b)3 – 3х2 = 0,
(1+k3)х3 + 3(bk2-1)х2 - 3bkx– 3х2 = 0.
Решаем систему
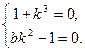
Откуда k = —1, b= 1. Следовательно, у = - x + 1 — наклонная асимптота рассматриваемой кривой.
№ 2. Исследовать и построить график неявно заданной функции
1. 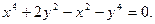
Решение.
Для нахождения области определения неявно заданной функций решаем заданное уравнение относительно у. Получаем
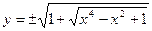 и
и 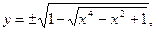
т. е. имеем две ветви кривой. В области определения обеих ветвей должно выполняться неравенство
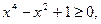 или
или 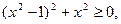
справедливое для 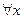 . Для точек второй ветви необходимо, чтобы
. Для точек второй ветви необходимо, чтобы 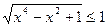 , или
, или 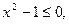 что возможно лишь при условии
что возможно лишь при условии 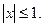
Следовательно, область определения первой ветви: 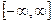 , область определения второй ветви: [—1; 1].
, область определения второй ветви: [—1; 1].
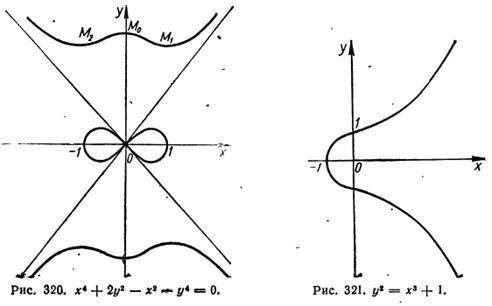
Кривая симметрична относительно осей координат. Горизонтальных и вертикальных асимптот она не имеет, поскольку коэффициенты при высших степенях х и у в уравнении постоянные. Находим наклонные асимптоты. Имеем
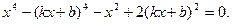
Приравниваем нулю коэффициенты при x4, х3 и получаем
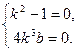
откуда k = ± 1, b = 0.
Следовательно, прямые у = х и у = -х - наклонные асимптоты рассматриваемой кривой.
Рассмотрим несколько дополнительных точек кривой. Для этого решим систему уравнений
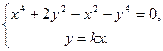
при различных значениях k:
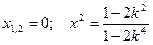
Эскиз графика представлен на рис. 320.
2. 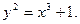
Решение.
Построить график функции
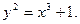
Решаем уравнение относительно y:
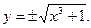
Функция определена при х 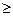 1. Кривая симметрична относительно оси абсцисс. Кривая асимптот не имеет.
1. Кривая симметрична относительно оси абсцисс. Кривая асимптот не имеет.
Для построения графика верхней ветви кривой записываем функцию 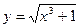 с помощью промежуточного аргумента t:
с помощью промежуточного аргумента t:
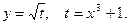
По графикам этих функций строим график верхней ветви кривой, а отобразив последнюю относительно оси абсцисс, получим график и нижней ветви кривой (рис. 321).
3. 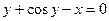
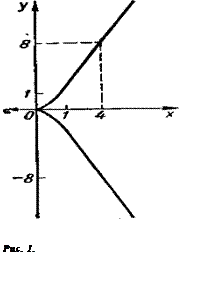
№ 3. Исследовать и построить график параметрически заданной функции
1. 
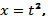
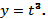
Решение.
Составим таблицу значений:
Построив найденные точки (x; у), получим искомую кривую.
-
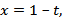
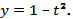
Решение.
В системе координат tOх строим график функции 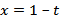 (рис. 2, а), а в системе координат tOy — график функции
(рис. 2, а), а в системе координат tOy — график функции 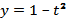 (рис. 2, б).
(рис. 2, б).
Теперь проводим исследование функции у=у(х).
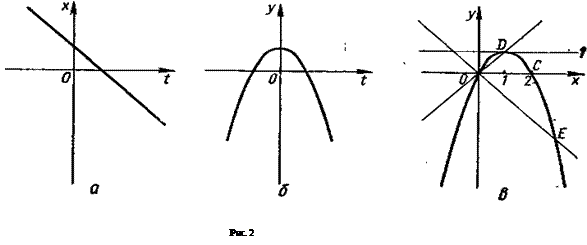
Область определения (см. рис. 2, а): (-∞; ∞). Область значений (см. рис. 2, б): (- ∞; 1].
Поскольку y(-t)=y(t), то t=0, т. е. x=1 - ось симметрии. Предельные значения функции: 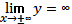
Точки пересечения с осями координат:
а) с осью ординат; решаем уравнение х=0, т.е. 1-t=0, откуда t=1; значение функции 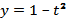 при t=1 равно у=0; с ледовательно, график функции у=у(х) пересекает ось ординат в точке (0; 0);
при t=1 равно у=0; с ледовательно, график функции у=у(х) пересекает ось ординат в точке (0; 0);
б) с осью абсцисс; решаем уравнение y=0, т. е. 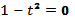 , получаем t=
, получаем t= 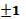 , соответственно
, соответственно 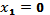 ,
, 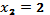 ; точки пересечения графика функции у = у(х) с осью абсцисс: О(0;0), С (2;0).
; точки пересечения графика функции у = у(х) с осью абсцисс: О(0;0), С (2;0).
Точки пересечения с биссектрисами координатных углов:
а) с биссектрисой y=x; решаем уравнение 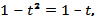 откуда
откуда 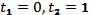 ; следовательно, график функции y=y(x) пересекает биссектрису y=x в точках D(1;1) и O(0;0);
; следовательно, график функции y=y(x) пересекает биссектрису y=x в точках D(1;1) и O(0;0);
б) с биссектрисой
y= -x; решаем уравнение
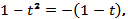
или
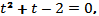
откуда
; следовательно, с биссектрисой
y= -x график функции
y=y(x) пересекается в точках О(0;0) и Е(3;-3).
Теперь выполняем построение графика функции у=у(х): проводим прямую у= 1 (график функции у = у (х) располагается ниже этой прямой), далее обозначим точки пересечения графика функции у = у (х) с осями координат и биссектрисами координатных углов: О, С, D, Е. График функции 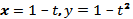 представлен на рис. 2, в.
представлен на рис. 2, в.
3. 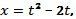
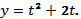
4. 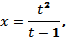
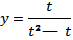
5. 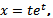
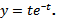
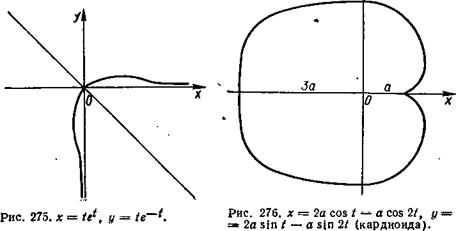
- х = 2а cos t — a cos 2t, у = 2а sin t — a sin 2t (кардиоида)
Решение.
Строим графики функций х = 2а cos t — a cos 2t,у = 2а sin t — a sin 2t.
Исследуем функцию y=y(x ). Область определения функции: [—За; а]. Область значений функции: [—2а; 2а]. График функции симметричен относительно оси абсцисс. Поскольку функции х = 2а cos t — a cos 2t, у = 2а sin t — a sin 2t периодические с периодом 2π, то и функция y=y(x) периодическая с периодом 2 π. Предельные значения функции у=у(х) на концах отрезка [0; 2 ] равны нулю. График представлен на рис. 276.
Занятие 15.
Тема занятия: «Полярные координаты. Графики функций в полярных координатах.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
Методические материалы.
Полярные координаты.

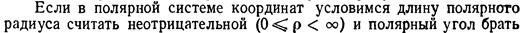

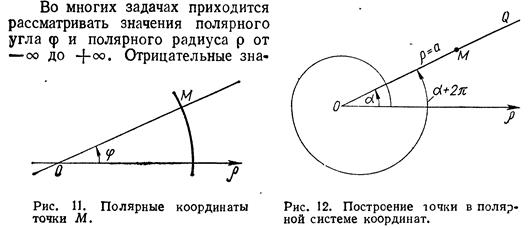

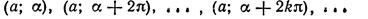
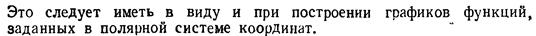
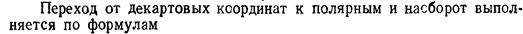
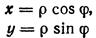
и
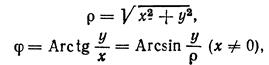




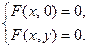
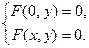
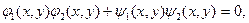
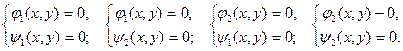
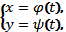
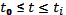 .
.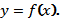 Сначала строят графики функций
Сначала строят графики функций 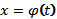 и
и 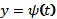 соответственно в системах координат
соответственно в системах координат 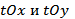 . Учитывая графическое изображение функций
. Учитывая графическое изображение функций 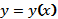 .
.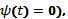 и находим соответствующее значение
и находим соответствующее значение 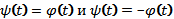 ,
,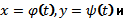 , которые при найденных t и дадут координаты искомых точек.
, которые при найденных t и дадут координаты искомых точек.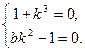
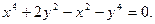
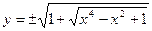 и
и 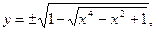
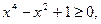 или
или 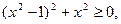
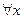 . Для точек второй ветви необходимо, чтобы
. Для точек второй ветви необходимо, чтобы 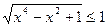 , или
, или 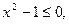 что возможно лишь при условии
что возможно лишь при условии 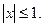
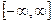 , область определения второй ветви: [—1; 1].
, область определения второй ветви: [—1; 1].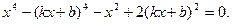
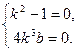
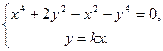
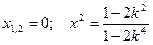

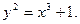
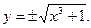
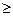 1. Кривая симметрична относительно оси абсцисс. Кривая асимптот не имеет.
1. Кривая симметрична относительно оси абсцисс. Кривая асимптот не имеет.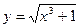 с помощью промежуточного аргумента t:
с помощью промежуточного аргумента t: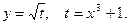
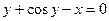

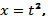
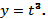
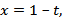
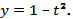
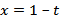 (рис. 2, а), а в системе координат tOy — график функции
(рис. 2, а), а в системе координат tOy — график функции 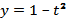 (рис. 2, б).
(рис. 2, б).
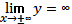
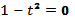 , получаем t=
, получаем t= 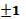 , соответственно
, соответственно 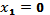 ,
, 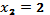 ; точки пересечения графика функции у = у(х) с осью абсцисс: О(0;0), С (2;0).
; точки пересечения графика функции у = у(х) с осью абсцисс: О(0;0), С (2;0).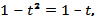 откуда
откуда 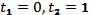 ; следовательно, график функции y=y(x) пересекает биссектрису y=x в точках D(1;1) и O(0;0);
; следовательно, график функции y=y(x) пересекает биссектрису y=x в точках D(1;1) и O(0;0);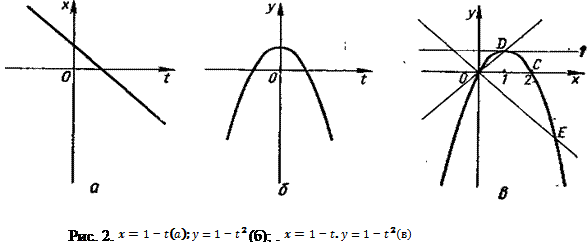
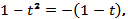 или
или 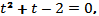 откуда
откуда 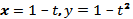 представлен на рис. 2, в.
представлен на рис. 2, в.